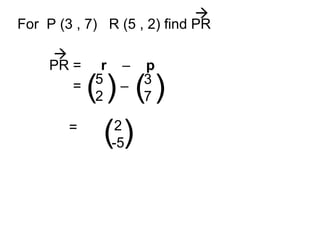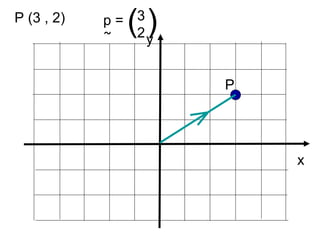
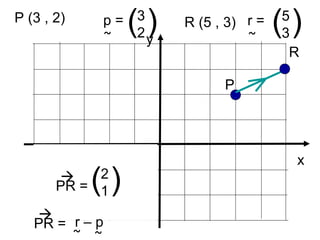
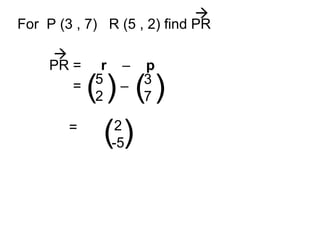
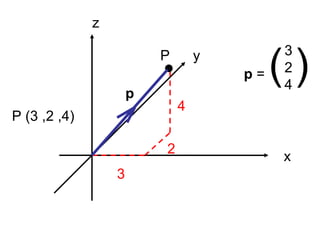
This document discusses position vectors in 2D and 3D coordinate systems. - A position vector starts at the origin and represents the displacement from the origin to a point P defined by its coordinates. - The position vector rule states that the position vector from point P to point R is equal to the vector from R's position vector subtracted by P's position vector. - Position vectors and their properties like magnitude, addition, subtraction, and scalar multiplication follow the same rules in 3D as in 2D. Several examples are provided to demonstrate calculating the position vector and magnitude between two points in 3D space.

1. Block 3
Position Vectors

2. What is to be learned?
• What a position vector is
• The position vector rule

3. A Position Vector
Starts at the origin

4. x
y
P
P (3 , 2) p = 3
2( )˜

5. x
y
P (3 , 2) p = 3
2( )˜
R
R (5 , 3) r = 5
3( )˜
PR =
 2
1( )
PR =

r – p
P

6. For P (3 , 7) R (5 , 2) find PR
PR = r – p
= –
=

5
2( ) 3
7( )
2
-5( )


7. Position Vectors
Start at Origin
If P = (a , b) then position vector
For coordinates G (2 , 5) and H (4 , 9)
p = a
b( )˜
GH =

h – g
˜˜
4
9( ) 2
5( )– 2
4( )==
Very Handy Rule

8. What is to be learned?
• Concept of 3D coordinates
• How 3D relates to vector stuff

9. x
y
z
3
2
4
p = ( )
3
2
4
P (3 ,2 ,4)
P
p

10. 3 D Vectors
Same rules as 2D for
• magnitude
• position vector rule
• addition
• subtraction
• multiplication by a scalar

11. For P (3 , 7, 4) R (5 , 8 , 7) find PR
PR = r – p

3
7
4
( )
5
8
7
( )

= –
2
1
3
= ( )
| PR2
| = 22
+ 12
+ 32
| PR| = √14


12. For P (-1 , 5, 8) R (5 , 8 , 7) find PR
PR = r – p

-1
5
8
( )
5
8
7
( )

= –
6
3
-1
= ( )
| PR2
| = 62
+ 32
+ (-1)2
| PR| = √46


13. 3 D Vectors
Same rules as 2D for
• magnitude
• position vector rule
• addition
• subtraction
• multiplication by a scalar
*

14. For P (-4 , 2, 9) R (5 , 8 , 7) find PR
PR = r – p

-4
2
9( )
5
8
7
( )

= –
9
6
-2
= ( )
| PR2
| = 92
+ 62
+ (-2)2
| PR| = √121

| PR| = 11


15. For P (-2 , 6, 9) R (3 , 7 , 8) find PR
PR = r – p

-2
6
9
( )
3
7
8
( )

= –
5
1
-1
= ( )
| PR2
| = 52
+ 12
+ (-1)2
| PR| = √27

Key Question
| PR| = 3√3
