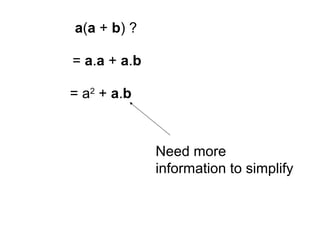
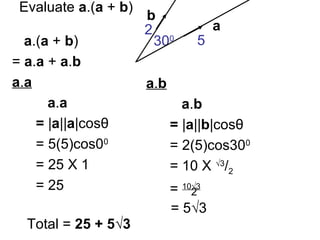
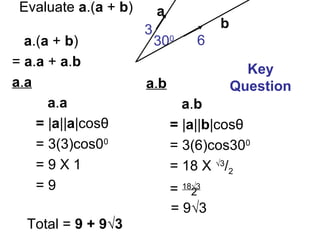
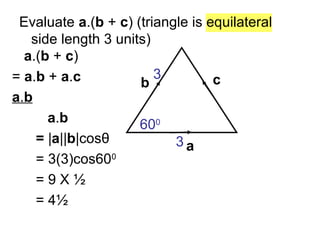
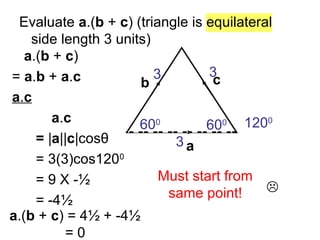
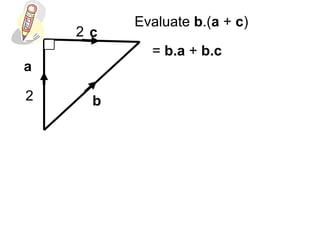
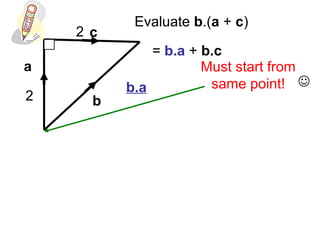
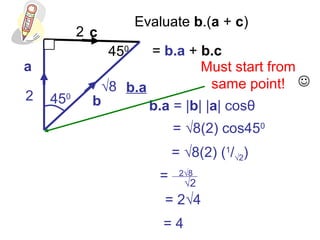
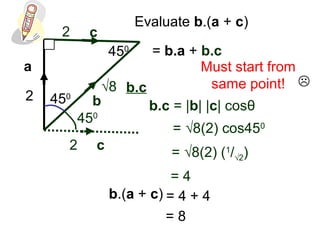
This document provides information about vectors, including: - The relationship between the magnitude of a vector and the cosine of the angle between two vectors in determining their dot product. - Unit vectors have a magnitude of 1 and are perpendicular to each other. - Examples are given of calculating the dot product of vectors in different geometric configurations by decomposing into the dot products of the vectors with the unit vectors. - Key steps are to start from the same point when calculating dot products of vectors in a figure.

1. Block 3
Vector Bits and Pieces

2. What is to be learned?
• Some wee footery bits about vectors

3. a.a ?
a.b = |a| |b| cosθ
a.a = |a| |a| cos00
a.a = |a| |a| (1)
a.a = a2

4. a(a + b) ?
= a.a + a.b
= a2
+ a.b
Need more
information to simplify

5. Unit Vectors
remember i j k
all have magnitude of 1
are at right angles to each other
i.i = i2 = 12
= 1 same for j.j and k.k
i.j = |i| |j| cosθ
= 1(1)cos900
= 0 same for i.k and j.k

6. Vector Bits and Pieces
• Breaking brackets works as normal
• a.a = a2
unit vectors
• i.i = j.j = k.k = 1
• i.j = j.k = i.k = 0
*
* i.i = i2

7. Evaluate a.(a + b)
a
b
a.(a + b)
= a.a + a.b
a.a
a.a
= |a||a|cosθ
= 5(5)cos00
= 25 X 1
= 25
300
2
5
a.b
a.b
= |a||b|cosθ
= 2(5)cos300
= 10 X √3
/2
= 10√3
2
= 5√3
Total = 25 + 5√3

8. Evaluate a.(a + b) a
b
a.(a + b)
= a.a + a.b
a.a
a.a
= |a||a|cosθ
= 3(3)cos00
= 9 X 1
= 9
300
3
6
a.b
a.b
= |a||b|cosθ
= 3(6)cos300
= 18 X √3
/2
= 18√3
2
= 9√3
Total = 9 + 9√3
Key
Question

9. Evaluate a.(b + c) (triangle is equilateral
side length 3 units)
a
b c
a.(b + c)
= a.b + a.c
a.b
a.b
= |a||b|cosθ
= 3(3)cos600
= 9 X ½
= 4½
600
3
3

10. Evaluate a.(b + c) (triangle is equilateral
side length 3 units)
a
b c
a.(b + c)
= a.b + a.c
a.c
a.c
= |a||c|cosθ
= 3(3)cos1200
= 9 X -½
= -4½
600
Must start from
same point!
3
3

600 1200
3
a.(b + c) = 4½ + -4½
= 0

11. b
c
Evaluate b.(a + c)
= b.a + b.c
2
a
2

12. a
b
c
Evaluate b.(a + c)
= b.a + b.c
2
2
b.a
Must start from
same point! 

13. b
c
Evaluate b.(a + c)
= b.a + b.c
2
b.a
a
2
b.a = |b| |a| cosθ
√8
450
450
= √8(2) cos450
= √8(2) (1
/√2)
= 2√4
Must start from
same point! 
= 2√8
√2
= 4

14. b
c
Evaluate b.(a + c)
= b.a + b.c
2
b.c
a
2
b.c = |b| |c| cosθ
√8
450
450
= √8(2) cos450
= √8(2) (1
/√2)
= 4
c2
450
b.(a + c) = 4 + 4
= 8
Must start from
same point! 