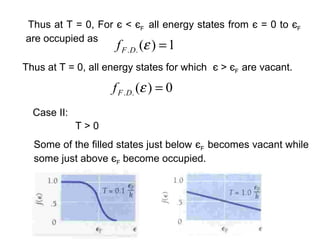
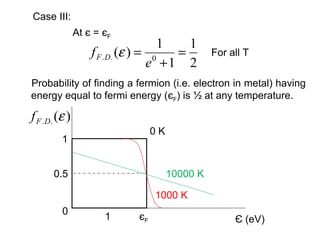
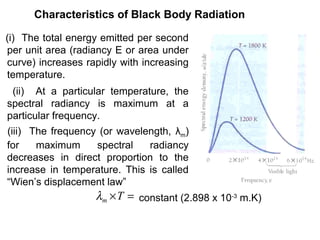
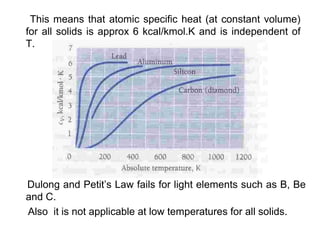
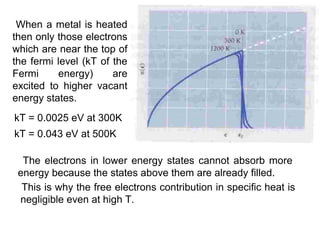
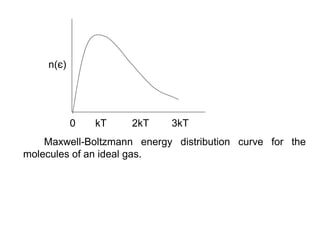
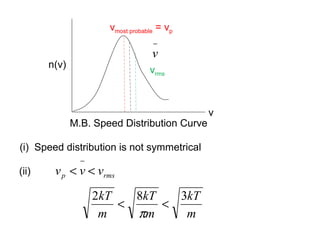
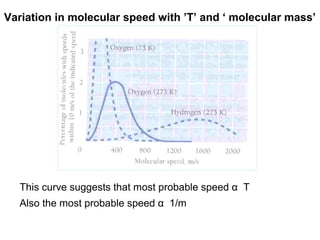
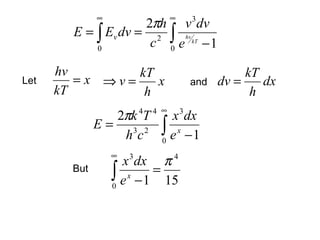This document discusses statistical mechanics and the distribution of energy among particles in a system. It provides 3 main types of statistical distributions based on the properties of identical particles: Maxwell-Boltzmann, Bose-Einstein, and Fermi-Dirac statistics. Maxwell-Boltzmann statistics applies to distinguishable particles, while Bose-Einstein and Fermi-Dirac apply to indistinguishable particles (bosons and fermions respectively), with the key difference being that fermions obey the Pauli exclusion principle. The document also discusses applications of these distributions, including the Maxwell-Boltzmann distribution law for molecular energies in an ideal gas.

1. Statistical Mechanics

2. Statistical Distribution
This determines the most probable way in which a certain total
amount of energy ‘E’ is distributed among the ‘N’ members of
a system of particles in thermal equilibrium at absolute
temperature, T.
Thus Statistical Mechanics reflects overall behavior of system
of many particles.
Suppose n(є) is the no. of particles having energy, є
then n(ε ) = g (ε ) f (ε )
where g(є) = no. of states of energy є or statistical weight
corresponding to energy є
f(є) = distribution function
= average no. of particles in each state of energy є
= probability of occupancy of each state of energy є

3. Statistical Distribution are of three kinds
1. Identical particles that are sufficiently far apart to be
distinguishable.
Example: molecules of a gas.
Negligible overlapping of ψ
Maxwell-Boltzmann Statistics
2. Indistinguishable identical particles of ‘0’ or integral spin.
Example: Bosons (don’t obey the exclusion principle)
Overlapping of ψ
Bose-Einstein Statistics
3. Indistinguishable identical particles with odd-half integral spin
(1/2, 3/2, 5/2 ..).
Example: Fermions (obey the exclusion principle)
Fermi-Dirac Statistics

4. Maxwell-Boltzmann Statistics
(Classical Approach)
According to this law number of identical and distinguishable
particles in a system at temperature, T having energy є is
n(є) = (No. of states of energy є).(average no. of particles in a
−ε state of energy є)
n(ε ) = g (ε ). Ae kT
(i)
−ε
Here A is a constant and f M . B. (ε ) = Ae kT
Equation (i) represents the Maxwell-Boltzmann Distribution Law
This law cannot explain the behavior of photons (Black body
radiation) or of electrons in metals (specific heat, conductivity)

5. Applications of M.B. Statistics
(i) Molecular energies in ideal gas
No. of molecules having energies between є and є + dє is given
by
n(ε )dε = {g (ε )dε }{ f (ε )}
−ε
n(ε ) = Ag (ε )e kT
dε (i)
The momentum of a molecule having energy є is given by
mdε
p = 2mε ⇒ dp =
2mε
No. of states in momentum space having momentum between
p and p + dp is proportional to the volume element i.e.
α ∫ ∫ ∫ dp x dp y dp z

6. 4 4 3
α π ( p + dp ) − πp
3
3 3
α 4πp 2 dp
g ( p )dp α 4πp 2 dp
g ( p )dp = Bp 2 dp B is a constant
Each momentum corresponds to a single є
g (ε )dε = Bp dp
2
mdε
g (ε )dε = B.2mε .
2mε

7. g (ε )dε = 2m 3 / 2 B ε dε
Put in (i)
No. of molecules with energy between є and є + dє
−ε
n(ε )dε = 2m BA ε e
3/ 2 kT
−ε
n(ε )dε = C ε e kT (ii)
Total No. of molecules is N
∞ ∞
N = ∫ n(ε )dε = C ∫ ε e
−ε
kT
dε
0 0

8. ∞
Using identity 1 π
∫ x e dx = 2a a
1
2 − ax
0
2πN
C=
(πkT ) 2
3
Put value of C in equation (ii)
2πN −ε
n(ε )dε = ε e kT dε
(πkT ) 2
3
This equation gives the number of molecules with energies
between є and є + dє in a sample of an ideal gas that
contains N molecules and whose absolute temperature is T. It
is called molecular energy distribution equation.

9. n(є)
0 kT 2kT 3kT
Maxwell-Boltzmann energy distribution curve for the
molecules of an ideal gas.

10. Average Molecular Energy
∞
Total energy of the system E = ∫ εn(ε )dε
0
∞
2πN
3 ∫
−ε
E= ε e kT dε
3
2
(πkT ) 2 0
Using ∞
3 π
∫x
− ax
dx = 2
3
2
e
0
4a a
2πN 3 
E=  4 (kT ) πkT 
2
(πkT ) 2
3
 

11. 3
E = NkT
2
− E
Average energy per molecule =ε =
N
−
3
ε = kT
2
This is the average molecular energy and is independent
of the molecular mass
At Room Temperature its value is 0.04 eV.

12. Equipartition of Energy: Equipartition Theorem
Average Kinetic Energy associated with each degree of freedom
of a molecule is 1
kT
2
Distribution of molecular speed
1 2
K .E. ⇒ ε = mv
2
⇒ dε = mvdv
Put this in molecular energy distribution equation

13. 3
 m  2 2 −mv2 2 kT
n(v)dv = 4πN   ve dv
 2πkT 
It is called molecular speed distribution formula.
RMS Speed
−
vrms = v 2
It is the square root of the average squared molecular speed
− 1 −2 3
ε = m v = kT
2 2
3kT
vrms =
m

14. Average Speed
∞
− 1
v = ∫ vn(v)dv
N0
3
∞
 m 
2
−mv 2
= 4π  ∫v e
3
 2 kT
dv
 2πkT  0
∞
1
∫x e
3 − ax 2
Using dx = 2
0
2a
3
−
 m 
2
 4k T 2 2
 8kT
v = 4π   .
 2m 2  =

 2πkT    πm

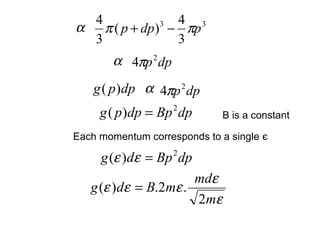
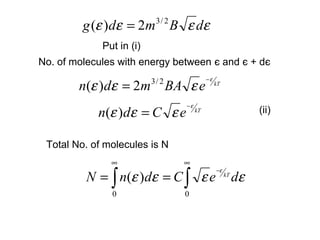
15. Most Probable Speed
3
 m  2 −mv2 2 kT
2
n(v) = 4πN   ve
 2πkT 
[ ]
3
dn(v)  m  d 2 −mv2 2 kT
2
= 4πN   ve =0
dv  2πkT  dv
3
 m 
2
4πN   ≠0
 2πkT 
dv
[
ve ]
d 2 −mv2 2 kT
=0 ⇒ vp =
2kT
m

16. vmost probable = vp
−
v
n(v)
vrms
v
M.B. Speed Distribution Curve
(i) Speed distribution is not symmetrical
−
(ii) v p < v < vrms
2kT 8kT 3kT
< <
m πm m

17. Variation in molecular speed with ’T’ and ‘ molecular mass’
This curve suggests that most probable speed α T
Also the most probable speed α 1/m

18. Quantum Statistics (Indistinguishable identical particles)
Bosons Fermions
1. ‘0’ or integral spin 1. Odd half integral spin
2. Do not obey exclusion 2. Obey exclusion principle
principle
3. Symmetric wave function 3. Anti-symmetric wave function
4. Any number of bosons 4. Only one fermion
can exist in the same can exist in a particular
quantum state of the quantum state of the
system system

19. Consider a system of two particles, 1 and 2, one of which is in
state ‘a’ and the other in state ‘b’.
When particles are distinguishable then
ψ ' = ψ a (1)ψ b (2)
ψ " = ψ a (2)ψ b (1)
When particles are indistinguishable then
1
For Bosons, ψ B = [ψ a (1)ψ b (2) +ψ a (2)ψ b (1)]
2
symmetric
1
For Fermions,ψ F = [ψ a (1)ψ b (2) −ψ a (2)ψ b (1)]
2
anti-symmetric

20. ψF becomes zero when ‘a’ is replaced with ‘b’ i.e.
1
ψF = [ψ a (1)ψ a (2) −ψ a (2)ψ a (1)] = 0
2
Thus two Fermions can’t exist in same state (Obey Exclusion
Principle)

21. Bose-Einstein Statistics
Any number of particles can exist in one quantum state.
Distribution function can be given by
1
f B. E . (ε ) = α ε
e e kT
−1
where α may be a function of temperature, T.
For Photon gas α = 0 ⇒ eα = 1
-1 in denominator indicates multiple occupancy of an energy
state by Bosons

22. Bose-Einstein Condensation
If the temperature of any gas is reduced, the wave packets grow
larger as the atoms lose momentum according to uncertainty
principle.
When the gas becomes very cold, the dimensions of the wave
packets exceeds the average atomic spacing resulting into
overlapping of the wave packets. If the atoms are bosons,
eventually, all the atoms fall into the lowest possible energy
state resulting into a single wave packet. This is called Bose-
Einstein condensation.
The atoms in such a Bose-Einstein condensate are barely
moving, are indistinguishable, and form one entity – a
superatom.

23. Fermi-Dirac Statistics
Obey Pauli’s exclusion Principle
Distribution function can be given by
1
f F .D. (ε ) = α ε
e e kT
+1
f (є) can never exceed 1, whatever be the value of α, є and T. So
only one particle can exist in one quantum state.
α is given by
εF
α =−
kT
where εF is the Fermi Energy

24. then
1
f F .D. (ε ) = ( ε −ε F )
e kT
+1
Case I:
T=0
(ε − ε F ) kT = −∞ For є < єF
(ε − ε F ) kT = +∞ For є > єF
For є < єF
1
f F .D. (ε ) = −∞
=1
e +1
For є > єF
1
f F .D. (ε ) = +∞
=0
e +1

25. Thus at T = 0, For є < єF all energy states from є = 0 to єF
are occupied as
f F .D. (ε ) = 1
Thus at T = 0, all energy states for which є > єF are vacant.
f F . D. (ε ) = 0
Case II:
T>0
Some of the filled states just below єF becomes vacant while
some just above єF become occupied.

26. Case III:
At є = єF
1 1
f F . D. (ε ) = 0 = For all T
e +1 2
Probability of finding a fermion (i.e. electron in metal) having
energy equal to fermi energy (єF) is ½ at any temperature.
f F . D. (ε )
0K
1
0.5 10000 K
1000 K
0
1 єF Є (eV)

27. Electromagnetic Spectrum
visible
microwaves infrared light ultraviolet x-rays
1000 100 10 1 0.1 0.01
Low High
Energy Energy
λ (µm)

28. Black Body Radiation
All objects radiate electromagnetic energy continuously
regardless of their temperatures.
Though which frequencies predominate depends on the
temperature.
At room temperature most of the radiation is in infrared part
of the spectrum and hence is invisible.
The ability of a body to radiate is closely related to its ability
to absorb radiation.
A body at a constant temperature is in thermal equilibrium
with its surroundings and must absorb energy from them at
the same rate as it emits energy.

29. A perfectly black body is the one which absorbs completely
all the radiation, of whatever wavelength, incident on it.
Since it neither transmits any radiation, it appears black
whatever the color of the incident radiation may be.
There is no surface available in practice which will absorb all
the radiation falling on it.
The cavity walls are constantly emitting and absorbing
radiation, and this radiation is known as black body
radiation.

30. Characteristics of Black Body Radiation
(i) The total energy emitted per second
per unit area (radiancy E or area under
curve) increases rapidly with increasing
temperature.
(ii) At a particular temperature, the
spectral radiancy is maximum at a
particular frequency.
(iii) The frequency (or wavelength, λm)
for maximum spectral radiancy
decreases in direct proportion to the
increase in temperature. This is called
“Wien’s displacement law”
λm ×T = constant (2.898 x 10-3 m.K)

31. Planck’s Radiation Law
Planck assumed that the atoms of the walls of cavity radiator
behave as oscillators with energy
ε n = nhv n = 0,1,2,3....
The average energy of an oscillator is
− ε
ε= N is total no. of Oscillators
N
− hv
ε = hv kT (i)
e −1
Thus the energy density (uv) of radiation in the frequency
range v to v + dv is
8πv dv −
2
uv dv = 3
×ε
c

32. 8πv 2 dv  hv 
uv dv = 3  hv kT 
c  e −1 
8πhv 3 dv
uv dv = 3
c e kT − 1
hv
This is Planck’s Radiation formula in terms of frequency.
In terms of wavelength
8πhc dλ
uλ dλ = 5 hc
λ e λkT − 1
This is Planck’s Radiation formula in terms of wavelength.

33. Case I : (Rayleigh-Jeans Law)
8πhc dλ
uλ dλ = 5 hc
λ e λkT − 1
hc hc
When λ is large then e λkT
≈ 1+
λkT
8πhc
u λ dλ = dλ
5 hc 
λ 1 + − 1
 λkT 
8πkT
u λ dλ = 4 dλ This is Rayleigh-Jeans
λ Law for longer λ’s.

34. Case II : (Wein’s Law)
8πhc dλ
uλ dλ = 5 hc
λ e λkT − 1
hc
When λ is very small then e λkT
>> 1
8πhc −hc λkT
u λ dλ = 5 e dλ
λ
This is Wein’s Law for small λ’s.
A B λkT
u λ dλ = 5 e dλ This is another form of
λ Wein’s Law..
Here A and B are constants.

35. Stefan’s Law
Planck’s Radiation formula in terms of frequency is
8πhv 3 dv
uv dv = 3
c e kT − 1
hv
c 2πhv 3 dv
uv dv = 2
c e kT − 1
hv
4
The spectral radiancy Ev is related to the energy density uv by
c
Ev = u v
4
2πh v dv
3
Ev dv = 2 hv
c e kT − 1

36. ∞ ∞
2πh v 3 dv
E = ∫ Ev dv = 2 ∫ hv
0
c 0 e kT − 1
hv kT kT
Let =x ⇒v= x and dv = dx
kT h h
4 ∞
2πk T 4
x dx 3
E= 3 2
hc ∫ ex −1
0
∞
x 3 dx π 4
But
∫ e x − 1 = 15
0

37. 2π 5 k 4 4
E= 3 2
T
15h c
2π 5 k 4
Let
3 2
= σ (Stefan’s constant)
15h c
E = σT 4
This is Stefan’s Law.
2π 5 k 4
Here σ= 3 2 = 5.67 x 10-5 erg/(cm2.sec.K4)
15h c
= 5.67 x 10-8 W/(m2.K4)

38. Wein’s Displacement Law
Planck’s Radiation formula in terms of frequency is
8πhc 1
uλ = 5 hc
λ e λkT − 1
d (uλ ) λ = λmax
Using =0 for
dλ
hc
= Constant
kTλmax
λm ×T = constant (2.898 x 10-3 m.K)
Peaks in Black Body radiation shifts to shorter wavelength
with increase in temperature.

39. Specific Heat of Solids
Atoms in solid behave as oscillators.
In case of solids total average energy per atom per degree
of freedom is kT (0.5kT from K.E. and 0.5kT from P.E.).
Each atom in the solid should have total energy = 3kT (3
degrees of freedom).
For one mole of solid, total energy, E = 3N okT (classically)
Here No is the Avogadro number.
E = 3RT
Specific heat at constant volume is
 ∂E 
Cv =   = 3R ~ 6 kcal/kmol.K
 ∂T V
This is Dulong & Petit’s Law.

40. This means that atomic specific heat (at constant volume)
for all solids is approx 6 kcal/kmol.K and is independent of
T.
Dulong and Petit’s Law fails for light elements such as B, Be
and C.
Also it is not applicable at low temperatures for all solids.

41. Einstein’s theory of Specific Heat of Solids
According to it the motion of the atoms in a solid is oscillatory.
The average energy per oscillator atom) is
− hv
ε = hv kT
e −1
The total energy for one mole of solid in three degrees of
freedom.
hv
E = 3 N o hv
e kT − 1
 ∂E 
The molar specific heat of solid is Cv =  
 ∂T V

42. hv 2
 hv  e
hv
 hv  e
kT kT
Cv = 3 N o hv 2  hv = 3N o k  
kT  (e kT − 1) 2 hv
  kT  (e − 1) 2 kT
2 hv
 hv  e kT
Cv = 3R  hv
 kT  (e kT − 1) 2
This is Einstein’s specific heat formula.
Case I:
At high T, kT >> hv then
hv hv
e kT
≈ 1+
kT

43.  hv 
2 1 + 
 hv   kT 
Cv ≈ 3 R  
 kT   hv  2
1 + − 1
 kT 
 hv 
C v ≈ 3 R 1 + 
 kT 
Cv ≈ 3R (∴ kT >> hv)
This is in agreement with Dulong & Petit’s Law at high T.

44. Case II: hv
At low T, hv >> kT then e kT
>> 1
2
 hv  −hv kT
Cv ≈ 3 R   e
 kT 
This implies that as T → 0, Cv → 0
i.e. is in agreement with experimental results at low T.

45. Free electrons in a metal
Typically, one metal atom gives one electron.
One mole atoms gives one mole of free electrons, (N o)
If each free electron can behave like molecules of an ideal gas.
Then
3 3
Average K.E. for 1 mole of electron gas,Ee = N o kT = RT
2 2
 ∂Ee  3
Molar specific heat of electron gas, ( Cv ) e =  = R
 ∂T V 2
Then total specific heat in metals at high T should be
3 9
Cv = 3 R + R = R
2 2

46. But experimentally at high T Cv ≈ 3 R
⇒ Free electrons don’t contribute in specific heat,
Why?
Electrons are fermions and have upper limit on the occupancy
of the quantum state.
By definition highest state of energy to be filled by a free
electron at T = 0 is obtained at є = єF
The no. of electrons having energy є is
εF
8 2πVm
3
2
N = ∫ g (ε )dε where g (ε )dε = ε dε
0
h3
Here V is the volume of the metal

47. εF
8 2πVm 16 2πVm 2 3 2
3 3
2
N=
h3 ∫
0
ε dε =
3h 3
εF
3
2
h  3N  2
⇒ εF =   (i)
2m  8πV 
where N/V is the density of free electrons.
Electron energy distribution
No. of electrons in the electron gas having energy between є
and є + dє is
n(ε )dε = g (ε ) f (ε )dε

48. 8 2πVm ε 2 ε
3 3
2
n(ε )dε = ( ε −ε F ) / kT
dε
h 3
e +1
using (i)
−3
 3N  ε 2 ε
n(ε )dε =   (ε −ε F ) / kT dε
 2 e +1
This is electron energy distribution formula, according to
which distribution of electrons can be found at different
temperatures.

49. When a metal is heated
then only those electrons
which are near the top of
the fermi level (kT of the
Fermi energy) are
excited to higher vacant
energy states.
kT = 0.0025 eV at 300K
kT = 0.043 eV at 500K
The electrons in lower energy states cannot absorb more
energy because the states above them are already filled.
This is why the free electrons contribution in specific heat is
negligible even at high T.

50. Average electron energy at 0K
Total energy at 0K is εF
Eo = ∫ εn(ε )dε
0
Since at 0K all electrons have energy less than or equal to єF
e (ε −ε F ) / kT = e −∞ = 0
εF
3 N −3 2 3 2 3N
Eo = ε F ∫ ε dε = εF
2 0 5
Then average electron energy
 −  Eo 3
ε o  = = εF at 0K.
  N 5