The document discusses the Discrete Fourier Transform (DFT). It explains that the DFT represents a finite-length sequence by the samples of its Discrete-Time Fourier Transform (DTFT). These samples are called the DFT coefficients of the sequence. The DFT provides a transformation between the time and frequency domains. It has various properties like linearity, duality, and relationships between shifting sequences and their DFTs. Circular convolution in the time domain can be computed as multiplication of DFT coefficients in the frequency domain. Examples are provided to illustrate these concepts.

1. The Discrete Fourier
Transform
Mr. HIMANSHU DIWAKAR JRTGI 1
Mr. HIMANSHU DIWAKAR
Assistant Professor
JETGI

2. Mr. HIMANSHU DIWAKAR JRTGI 2

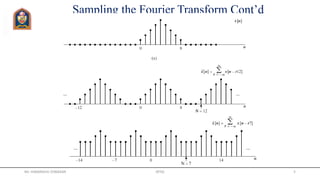
3. Sampling the Fourier Transform
• Consider an aperiodic sequence with a Fourier transform
• Assume that a sequence is obtained by sampling the DTFT
• Since the DTFT is periodic resulting sequence is also periodic
• We can also write it in terms of the z-transform
• The sampling points are shown in figure
• could be the DFS of a sequence
• Write the corresponding sequence
     
 
 kN/2j
kN/2
j
eXeXkX
~ 



 
  jDTFT
eX]n[x
     
 
 kN/2j
ez
eXzXkX
~
kN/2


 
 kX
~
   





1N
0k
knN/2j
ekX
~
N
1
]n[x~
Mr. HIMANSHU DIWAKAR JRTGI 3

4. Sampling the Fourier Transform Cont’d
• The only assumption made on the sequence is that DTFT exist
• Combine equation to get
• Term in the parenthesis is
• So we get
   




m
mjj
emxeX    





1N
0k
knN/2j
ekX
~
N
1
]n[x~
   
 kN/2j
eXkX
~ 

     
     
    
 



























mm
1N
0k
mnkN/2j
1N
0k
knN/2j
m
kmN/2j
mnp~mxe
N
1
mx
eemx
N
1
]n[x~
     
 






r
1N
0k
mnkN/2j
rNmne
N
1
mnp~
     





rr
rNnxrNnnx]n[x~
Mr. HIMANSHU DIWAKAR JRTGI 4

5. Sampling the Fourier Transform Cont’d
Mr. HIMANSHU DIWAKAR JRTGI 5

6. Sampling the Fourier Transform Cont’d
• Samples of the DTFT of an aperiodic sequence
• can be thought of as DFS coefficients
• of a periodic sequence
• obtained through summing periodic replicas of original sequence
• If the original sequence
• is of finite length
• and we take sufficient number of samples of its DTFT
• the original sequence can be recovered by
• It is not necessary to know the DTFT at all frequencies
• To recover the discrete-time sequence in time domain
• Discrete Fourier Transform
• Representing a finite length sequence by samples of DTFT
   


 

else0
1Nn0nx~
nx
Mr. HIMANSHU DIWAKAR JRTGI 6

7. The Discrete Fourier Transform
• Consider a finite length sequence x[n] of length N
• For given length-N sequence associate a periodic sequence
• The DFS coefficients of the periodic sequence are samples of the DTFT of x[n]
• Since x[n] is of length N there is no overlap between terms of x[n-rN] and we can
write the periodic sequence as
• To maintain duality between time and frequency
• We choose one period of as the Fourier transform of x[n]
  1Nn0ofoutside0nx 
   



r
rNnxnx~
        NkXNmodkXkX
~

 kX
~
   



 

else0
1Nk0kX
~
kX
        NnxNmodnxnx~ 
Mr. HIMANSHU DIWAKAR JRTGI 7

8. The Discrete Fourier Transform Cont’d
• The DFS pair
• The equations involve only on period so we can write
• The Discrete Fourier Transform
• The DFT pair can also be written as
   





1N
0k
knN/2j
ekX
~
N
1
]n[x~
   





1N
0n
knN/2j
e]n[x~kX
~
 
 





 



else0
1Nk0e]n[x~
kX
1N
0n
knN/2j
   





 



else0
1Nk0ekX
~
N
1
]n[x
1N
0k
knN/2j
   





1N
0n
knN/2j
e]n[xkX    





1N
0k
knN/2j
ekX
N
1
]n[x
  ]n[xkX DFT
 
Mr. HIMANSHU DIWAKAR JRTGI 8

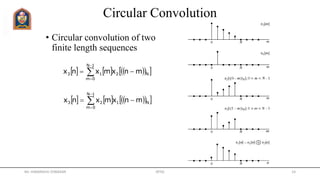
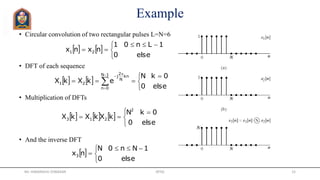
9. Example
• The DFT of a rectangular pulse
• x[n] is of length 5
• We can consider x[n] of any
length greater than 5
• Let’s pick N=5
• Calculate the DFS of the
periodic form of x[n]
   
 


 










else0
,...10,5,0k5
e1
e1
ekX
~
5/k2j
k2j
4
0n
n5/k2j
Mr. HIMANSHU DIWAKAR JRTGI 9

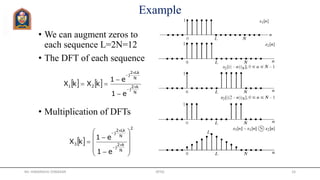
10. Example Cont’d
• If we consider x[n] of length 10
• We get a different set of DFT
coefficients
• Still samples of the DTFT but in
different places
Mr. HIMANSHU DIWAKAR JRTGI 10

11. Properties of DFT
• Linearity
• Duality
• Circular Shift of a Sequence
   
   
       kbXkaXnbxnax
kXnx
kXnx
21
DFT
21
2
DFT
2
1
DFT
1
 
 
 
   
       mN/k2jDFT
N
DFT
ekX1-Nn0mnx
kXnx

 
 
   
     N
DFT
DFT
kNxnX
kXnx
 
 
Mr. HIMANSHU DIWAKAR JRTGI 11

12. Example: Duality
Mr. HIMANSHU DIWAKAR JRTGI 12

13. Symmetry Properties
Mr. HIMANSHU DIWAKAR JRTGI 13

14. Circular Convolution
• Circular convolution of two
finite length sequences
       



1N
0m
N213 mnxmxnx
       



1N
0m
N123 mnxmxnx
Mr. HIMANSHU DIWAKAR JRTGI 14

15. Example
• Circular convolution of two rectangular pulses L=N=6
• DFT of each sequence
• Multiplication of DFTs
• And the inverse DFT
   


 

else0
1Ln01
nxnx 21
   


 
 




else0
0kN
ekXkX
1N
0n
kn
N
2
j
21
     


 

else0
0kN
kXkXkX
2
213
 


 

else0
1Nn0N
nx3
Mr. HIMANSHU DIWAKAR JRTGI 15

16. Example
• We can augment zeros to
each sequence L=2N=12
• The DFT of each sequence
• Multiplication of DFTs
   
N
k2
j
N
Lk2
j
21
e1
e1
kXkX 






 
2
N
k2
j
N
Lk2
j
3
e1
e1
kX












 



Mr. HIMANSHU DIWAKAR JRTGI 16

17. THANK YOU
Mr. HIMANSHU DIWAKAR JRTGI 17