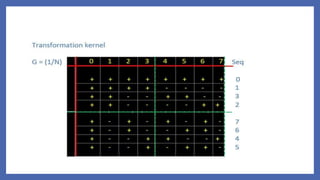
The document compares the Walsh and Haar transforms used in digital image processing. It outlines the mathematical formulations for both forward and inverse transforms, highlighting the similarities and differences in terms of energy compaction and speed of computation. While the Walsh transform features more complex energy distribution, the Haar transform is noted for its speed and orthogonality, albeit with a weaker energy compaction for images.

1. DISTINGUISH BETWEEN
WALSH TRANSFORM
AND
HAAR TRANSFORM
DIGITAL IMAGE PROCESSING
NITHIN KALLEPALLY

2. WALSH TRANSFORM
• 1DWalshTransform kernel is given by:
• n - 1
• g(x, u) = (1/N) ∏ (-1) bi(x) bn-1-i(u)
• i = 0
• where, N – no. of samples
• n – no. of bits needed to represent x as well as u
• bk(z) – kth bits in binary representation of z.
• Thus, Forward DiscreteWalshTransformation is
N - 1 n - 1
• W(u) = (1/N) Σ f(x) ∏ (-1) bi(x)b(u)
x = 0 i = 0

3. • 1D InverseWalshTransform kernel is given by:
• n - 1
• h(x, u) =∏ (-1) bi(x) bn-1-i(u)
• i = 0
•
• Thus, Inverse DiscreteWalshTransformation is given by
N - 1 n - 1
• f(x) =Σ W(u) ∏ (-1) bi(x) bn-1-i(u)
u = 0 i = 0
•
• Thus, both the transforms are identical except the factor of (1/N).
Same algorithm is used to perform forward and inverse
transformation.

4. • 2D signals:
• ForwardTransformation kernel is given by:
N - 1
• g(x, y, u, v) = (1/N) ∏ (-1) {b (x) b(u) + b (y) b(v)}
i = 0 I n-1-I I n-1-i
• InverseTransformation kernel is given by:
h(x, y, u, v) = (1/N) ∏ (-1) {b (x) bn-1-i(u) + b (y) bi
n-1-
i

5. i
2D Forward WalshTransform is given by

6. Basis Function for Walsh
Transformation:

7. WalshTransformation applied
on image:

8. • PROPERTIES :
• The transform is separable and symmetric.
• The coefficients near origin have maximum energy
andit reduces as we go further away from the origin.
• It has energy compaction property but NOT so strong as in
DCT.

10. HAAR TRANSFORM

12. PROPERTIES
• The Haar transform is real and orthogonal
• The Haar transform is very fast.It can implement n operations pn
an Nx1 vector.
• The mean vectors of the haar matrix are sequentially ordered.
• It has a poor energy deal for images

13. THANK YOU…