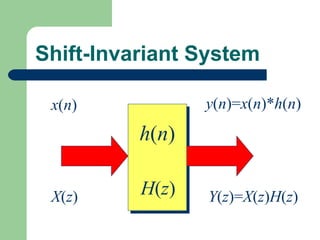
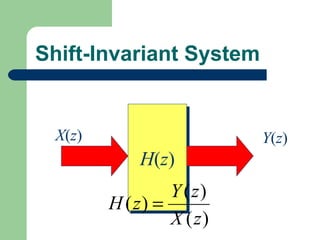
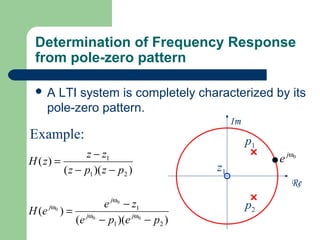
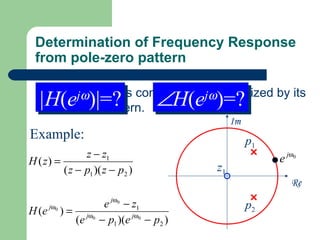
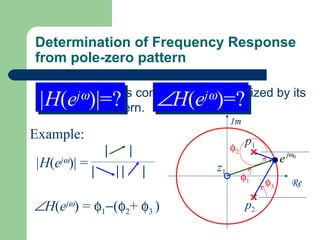
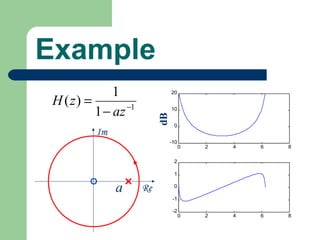
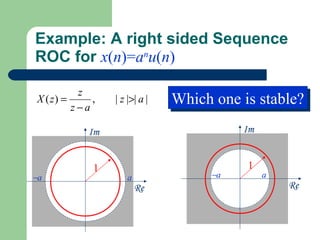
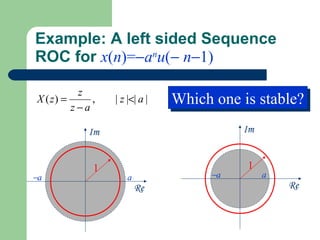
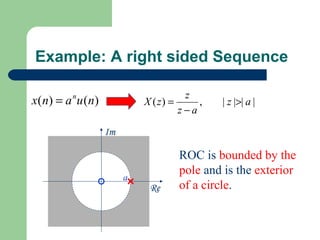
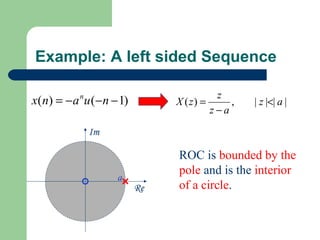
The z-transform provides a method to analyze discrete-time signals and systems using complex variable theory. It is defined as the summation of a sequence multiplied by z to the power of the time index from negative infinity to positive infinity. The region of convergence consists of values of z where this summation converges. It is determined by the locations of the zeros and poles of the z-transform function. Examples show how different sequences lead to different regions of convergence bounded by these zeros and poles.

1. The z-Transform
主講人：虞台文

2. Content
 Introduction
 z-Transform
 Zeros and Poles
 Region of Convergence
 Important z-Transform Pairs
 Inverse z-Transform
 z-Transform Theorems and Properties
 System Function

3. The z-Transform
Introduction

4. Why z-Transform?
A generalization of Fourier transform
 Why generalize it?
– FT does not converge on all sequence
– Notation good for analysis
– Bring the power of complex variable theory deal with
the discrete-time signals and systems

5. The z-Transform
z-Transform

6. Definition
 The z-transform of sequence x(n) is defined by
∞
X ( z) = ∑ x ( n) z
n = −∞
−n
Fourier
Transform
 Let z = e−jω.
∞
X (e ) = jω
∑ x ( n )e
n =−∞
− jω n

7. z-Plane
∞
∑ x ( n) z −n Im
X ( z) =
n = −∞
z = e−jω
ω
∞ Re
jω
X (e ) = ∑ x ( n )e
n =−∞
− jω n
Fourier Transform is to evaluate z-transform
Fourier Transform is to evaluate z-transform
on a unit circle.
on a unit circle.

8. z-Plane
Im
X(z)
z = e−jω
ω
Re
Im
Re

9. Periodic Property of FT
X(ejω)
X(z)
−π π ω
Im
Re Can you say why Fourier Transform is
Can you say why Fourier Transform is
aaperiodic function with period 2π?
periodic function with period 2π?

10. The z-Transform
Zeros and Poles

11. Definition
 Give a sequence, the set of values of z for which the
z-transform converges, i.e., |X(z)|<∞, is called the
region of convergence.
∞ ∞
| X ( z ) |= ∑ x ( n) z − n =
n = −∞
∑ | x(n) || z |− n < ∞
n = −∞
ROC is centered on origin and
ROC is centered on origin and
consists of a set of rings.
consists of a set of rings.

12. Example: Region of Convergence
∞ ∞
| X ( z ) |= ∑ x ( n) z − n =
n = −∞
∑ | x(n) || z |− n < ∞
n = −∞
Im ROC is an annual ring centered
ROC is an annual ring centered
on the origin.
on the origin.
r
Re Rx − <| z |< Rx +
jω
ROC = {z = re | Rx − < r < Rx + }

13. Stable Systems
A stable system requires that its Fourier transform is
uniformly convergent.
Im  Fact: Fourier transform is to
evaluate z-transform on a unit
circle.
1
 A stable system requires the
Re ROC of z-transform to include
the unit circle.

14. Example: A right sided Sequence
x ( n) = a n u ( n)
x(n)
... n
-8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10

15. Example: A right sided Sequence
For convergence of X(z), we
x ( n) = a u ( n)
n
require that
∞
∑
∞
| az −1 | < ∞ | az −1 |< 1
X ( z) = ∑ a u (n)z
n = −∞
n −n
n =0
∞ | z |>| a |
= ∑ a n z −n ∞
1 z
n =0 X ( z ) = ∑ (az ) =
−1 n
−1
=
∞ n =0 1 − az z−a
= ∑ (az −1 ) n
| z |>| a |
n =0

16. Example: A right sided Sequence
ROC for x(n)=anu(n)
z
X ( z) =
z−a
, | z |>| a | Which one is stable?
Which one is stable?
Im Im
1 1
−a a −a a
Re Re

17. Example: A left sided Sequence
x(n) = −a nu (−n − 1)
-8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10
... n
x(n)

18. Example: A left sided Sequence
For convergence of X(z), we
x(n) = −a u (−n − 1)n
require that
∞ ∞
X ( z ) = − ∑ a u (− n − 1)z
∑ | a −1 z | < ∞
−n
| a −1 z |< 1
n
n = −∞
−1
n =0
= − ∑ a n z −n
n = −∞
| z |<| a |
∞
= −∑ a − n z n ∞
1 z
n =1 X ( z ) = 1 − ∑ (a z ) = 1 −
−1 n
−1
=
∞ n=0 1− a z z − a
= 1 − ∑ a −n z n
n =0 | z |<| a |

19. Example: A left sided Sequence
ROC for x(n)=−anu(− n−1)
z
X ( z) =
z−a
, | z |<| a | Which one is stable?
Which one is stable?
Im Im
1 1
−a a −a a
Re Re

20. The z-Transform
Region of
Convergence

21. Represent z-transform as a
Rational Function
P( z ) where P(z) and Q(z) are
X ( z) = polynomials in z.
Q( z )
Zeros: The values of z’s such that X(z) = 0
Poles: The values of z’s such that X(z) = ∞

22. Example: A right sided Sequence
z
x ( n) = a n u ( n) X ( z) = , | z |>| a |
z−a
Im
ROC is bounded by the
pole and is the exterior
a
Re of a circle.

23. Example: A left sided Sequence
z
x(n) = −a nu (−n − 1) X ( z) = , | z |<| a |
z−a
Im
ROC is bounded by the
pole and is the interior
a
Re of a circle.

24. Example: Sum of Two Right Sided Sequences
x ( n) = ( 1 ) n u ( n) + ( − 1 ) n u ( n)
2 3
z z 2 z ( z − 12 )
1
X ( z) = + =
z−2 z+3
1 1
( z − 1 )( z + 1 )
2 3
Im
ROC is bounded by poles
and is the exterior of a circle.
1/12
−1/3 1/2 Re
ROC does not include any pole.

25. Example: A Two Sided Sequence
x(n) = (− 1 ) n u (n) − ( 1 ) n u (−n − 1)
3 2
z z 2 z ( z − 12 )
1
X ( z) = + =
z+3 z−2
1 1
( z + 1 )( z − 1 )
3 2
Im
ROC is bounded by poles
and is a ring.
1/12
−1/3 1/2 Re
ROC does not include any pole.

26. Example: A Finite Sequence
x ( n) = a n , 0 ≤ n ≤ N −1
N −1 N −1
1 − (az −1 ) N 1 zN − aN
X ( z) = ∑ a z n −n
= ∑ ( az )
−1 n
= = N −1
n =0 n =0 1 − az −1 z z−a
Im
N-1 zeros
ROC: 0 < z < ∞
N-1 poles ROC does not include any pole.
Re
Always Stable
Always Stable

27. Properties of ROC
 A ring or disk in the z-plane centered at the origin.
 The Fourier Transform of x(n) is converge absolutely iff the ROC
includes the unit circle.
 The ROC cannot include any poles
 Finite Duration Sequences: The ROC is the entire z-plane except
possibly z=0 or z=∞.
 Right sided sequences: The ROC extends outward from the outermost
finite pole in X(z) to z=∞.
 Left sided sequences: The ROC extends inward from the innermost
nonzero pole in X(z) to z=0.

28. More on Rational z-Transform
Consider the rational z-transform
with the pole pattern:
Im
Find the possible
Find the possible a b c
ROC’s
ROC’s Re

29. More on Rational z-Transform
Consider the rational z-transform
with the pole pattern:
Im
Case 1: A right sided Sequence.
a b c
Re

30. More on Rational z-Transform
Consider the rational z-transform
with the pole pattern:
Im
Case 2: A left sided Sequence.
a b c
Re

31. More on Rational z-Transform
Consider the rational z-transform
with the pole pattern:
Im
Case 3: A two sided Sequence.
a b c
Re

32. More on Rational z-Transform
Consider the rational z-transform
with the pole pattern:
Im
Case 4: Another two sided Sequence.
a b c
Re

33. The z-Transform
Important
z-Transform Pairs

34. Z-Transform Pairs
Sequence z-Transform ROC
δ(n) 1 All z
All z except 0 (if m>0)
δ( n − m ) z −m
or ∞ (if m<0)
1
u (n) | z |> 1
1 − z −1
1
− u (−n − 1) | z |< 1
1 − z −1
1
n
a u (n) | z |>| a |
1 − az −1
1
− a nu (−n − 1) | z |<| a |
1 − az −1

35. Z-Transform Pairs
Sequence z-Transform ROC
1 − [cos ω0 ] z −1
[cos ω0 n]u (n) | z |> 1
1 − [ 2 cos ω0 ]z −1 + z −2
[sin ω0 ]z −1
[sin ω0 n]u (n) | z |> 1
1 − [2 cos ω0 ]z −1 + z −2
1 − [ r cos ω0 ]z −1
[r n cos ω0 n]u (n) | z |> r
1 − [ 2r cos ω0 ]z −1 + r 2 z − 2
[r sin ω0 ] z −1
[r n sin ω0 n]u (n) | z |> r
1 − [ 2r cos ω0 ]z −1 + r 2 z − 2
a n 0 ≤ n ≤ N −1 1− aN z−N
 | z |> 0
0 otherwise 1 − az −1

36. The z-Transform
Inverse z-Transform

37. The z-Transform
z-Transform Theorems
and Properties

38. Linearity
Z [ x(n)] = X ( z ), z ∈ Rx
Z [ y (n)] = Y ( z ), z ∈ Ry
Z [ax(n) + by (n)] = aX ( z ) + bY ( z ), z ∈ Rx ∩ R y
Overlay of
the above two
ROC’s

39. Shift
Z [ x(n)] = X ( z ), z ∈ Rx
Z [ x(n + n0 )] = z X ( z )
n0
z ∈ Rx

40. Multiplication by an Exponential Sequence
Z [ x(n)] = X ( z ), Rx- <| z |< Rx +
−1
Z [a x(n)] = X (a z )
n
z ∈| a | ⋅Rx

41. Differentiation of X(z)
Z [ x(n)] = X ( z ), z ∈ Rx
dX ( z )
Z [nx(n)] = − z z ∈ Rx
dz

42. Conjugation
Z [ x(n)] = X ( z ), z ∈ Rx
Z [ x * (n)] = X * ( z*) z ∈ Rx

43. Reversal
Z [ x(n)] = X ( z ), z ∈ Rx
−1
Z [ x(−n)] = X ( z ) z ∈ 1 / Rx

44. Real and Imaginary Parts
Z [ x(n)] = X ( z ), z ∈ Rx
Re[ x(n)] = 1 [ X ( z ) + X * ( z*)]
2 z ∈ Rx
Im[ x(n)] = 1
2j [ X ( z ) − X * ( z*)] z ∈ Rx

45. Initial Value Theorem
x(n) = 0, for n < 0
x(0) = lim X ( z )
z →∞

46. Convolution of Sequences
Z [ x(n)] = X ( z ), z ∈ Rx
Z [ y (n)] = Y ( z ), z ∈ Ry
Z [ x(n) * y (n)] = X ( z )Y ( z ) z ∈ Rx ∩ R y

47. Convolution of Sequences
∞
x ( n) * y ( n) = ∑ x(k ) y (n − k )
k = −∞
 ∞
∞
 −n
Z [ x(n) * y (n)] = ∑  ∑ x(k ) y (n − k )  z
n = −∞  k = −∞ 
∞ ∞ ∞ ∞
= ∑ x(k ) ∑ y(n − k )z −n
= ∑
k = −∞
x(k ) z − k ∑ y (n)z − n
n = −∞
k = −∞ n = −∞
= X ( z )Y ( z )

48. The z-Transform
System Function

49. Shift-Invariant System
x(n) y(n)=x(n)*h(n)
h(n)
h(n)
X(z) H(z) Y(z)=X(z)H(z)

50. Shift-Invariant System
X(z) Y(z)
H(z)
H(z)
Y ( z)
H ( z) =
X ( z)

51. Nth-Order Difference Equation
N M
∑a
k =0
k y (n − k ) = ∑ br x(n − r )
r =0
N M
Y ( z )∑ ak z − k = X ( z )∑ br z − r
k =0 r =0
M N
−r −k
H ( z ) = ∑ br z ∑ ak z
r =0 k =0

52. Representation in Factored Form
Contributes poles at 0 and zeros at cr
M
A∏ (1 − cr z −1 )
H ( z) = N
r =1
∏ (1 − d r z −1 )
k =1
Contributes zeros at 0 and poles at dr

53. Stable and Causal Systems
Causal Systems : ROC extends outward from the outermost pole.
Im
M
A∏ (1 − cr z −1 )
H ( z) = N
r =1
Re
∏ (1 − d r z −1 )
k =1

54. Stable and Causal Systems
Stable Systems : ROC includes the unit circle.
Im
M
A∏ (1 − cr z −1 ) 1
H ( z) = N
r =1
Re
∏ (1 − d r z −1 )
k =1

55. Example
Consider the causal system characterized by
y (n) = ay (n − 1) + x(n) Im
1 1
H ( z) =
1 − az −1 a Re
h( n) = a n u ( n)

56. Determination of Frequency Response
from pole-zero pattern
A LTI system is completely characterized by its
pole-zero pattern.
Im
Example: p1
z − z1 e j ω0
H ( z) =
( z − p1 )( z − p2 ) z1
Re
e jω0 − z1 p2
H (e jω0 ) =
(e jω0 − p1 )(e jω0 − p2 )

57. Determination of Frequency Response
from pole-zero pattern
∠H(e )=?
A LTIjjω
system is completely characterized by its
|H(e )|=?
|H(e )|=?ω
pole-zero pattern.
ω
jjω
∠H(e )=?
Im
Example: p1
z − z1 e j ω0
H ( z) =
( z − p1 )( z − p2 ) z1
Re
e jω0 − z1 p2
H (e jω0 ) =
(e jω0 − p1 )(e jω0 − p2 )

58. Determination of Frequency Response
from pole-zero pattern
∠H(e )=?
A LTIjjω
system is completely characterized by its
ω
|H(e )|=?
|H(e )|=?
pole-zero pattern.
ω
jjω
∠H(e )=?
Im
Example: p1
| | φ2
jω
|H(e )| = e j ω0
| || | z1
φ1 φ3 Re
∠H(ejω) = φ1−(φ2+ φ3 ) p2

59. Example
1 20
H ( z) = −1
1 − az 10
dB
0
Im
-10
0 2 4 6 8
2
1
a Re 0
-1
-2
0 2 4 6 8