Download as PDF, PPTX
![Discharge over Triangular Notch (V-Notch)
37
In order to obtain discharge over
whole area we must integrate above
equation from h=0 to h=H, therefore;
( )[ ]2/5
2/tan2
15
8
HgCQ dact θ=](https://image.slidesharecdn.com/flowmeasurement-150316030307-conversion-gate01/85/Flow-measurement-37-320.jpg)
![Discharge over Triangular Notch (V-Notch)
44
In order to obtain discharge over
whole area we must integrate above
equation from h=0 to h=H, therefore;
( ) ( )( )( )
( ) ( ) dhhhHgQ
ghhHdhQ
H
H
∫
∫
−=
−=
0
0
2/tan22
22/tan2
θ
θ
( ) ( )
( )
=
−= ∫
2/5
0
2/32/1
15
4
2/tan22
2/tan22
HgQ
dhhHhgQ
H
θ
θ
( )[ ]2/5
2/tan2
15
8
HgQ θ=
( )[ ]2/5
2/tan2
15
8
HgCQ dact θ=](https://image.slidesharecdn.com/flowmeasurement-150316030307-conversion-gate01/85/Flow-measurement-44-320.jpg)
Uploaded byMohsin Siddique
Flow measurement
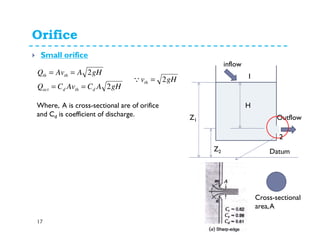
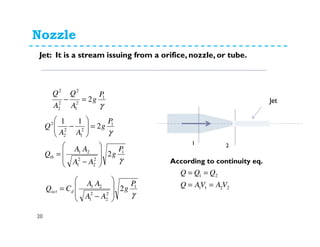
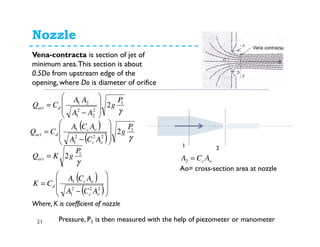
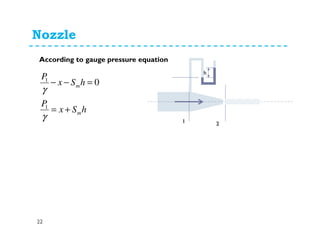
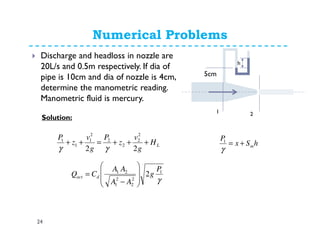
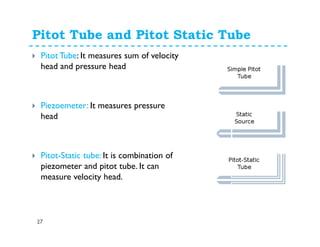
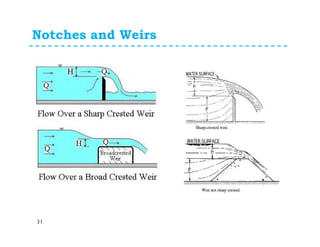
This document discusses various flow measurement techniques including venturimeters, orifices, mouthpieces, pitot tubes, weirs and notches. It provides detailed explanations and equations for venturimeters and orifices. Venturimeters use the Bernoulli's equation to relate the pressure difference between two sections to the flow rate. Orifices use the relationship between head loss and flow rate. The document also defines various coefficients used in flow measurements like coefficient of contraction, velocity, and discharge. It discusses types of venturimeters and orifices based on their orientation and geometry.
More Related Content
![Engineering Economics: Solved exam problems [ch1-ch4]](https://cdn.slidesharecdn.com/ss_thumbnails/solvedexamproblemsch1-ch4-200220070043-thumbnail.jpg?width=640&height=640&fit=bounds)
Flow measurement
- 1. Flow Measurement: Venturimeter,Orifices and Mouthpieces, Pitot tube, Pitot static tube, Weirs and notches. Dr. Mohsin Siddique Assistant Professor 1 Fluid Mechanics
- 2. Flow Measurement 2 Pipes (pressureconduits) Open channel (flumes, canals and rivers etc) 1. Venturimeter 2. Orifices 3. Orifice meter 4. Mouth pieces/tubes 5. Nozzle 6. Pitot static tube 1. Notches (Rectangular notch,V notch) 2. Weirs
- 3. Flow Measurement inPipes 3 Venturimeter
- 4. Flow Measurements inPipes 4 Venturimeter According to Bernoulli's Equation between section 1 and 2 we can write; g v z P g v z P 22 2 2 2 2 2 1 1 1 ++=++ γγ ( )21 21 2 2 2 1 21 22 zzg PP g AA AA CQ dact −+ − − = γγ Figure shows a venturimeter in which discharge Q is flowing, Let, D1 is diameter, A1 is cross-section area, P1 is pressure, z1 is elevation headV1 is velocity at section 1. Similarly D2 ,A2, P2, z2 &V2 are corresponding values at section 2 D1,A1, P1, Z1,V1 D2,A2, P2, Z2,V2 ( ) 2 1 2 221 21 22 vvzzg PP g −=−+ − γγ Datum Direction of flow
- 5. Flow Measurements inPipes 5 Venturimeter ( ) 2 1 2 2 2 2 21 21 22 A Q A Q zzg PP g −=−+ − γγ 2211 VAVAQ ==Q ( ) 2 2 1 2 2 21 21 11 22 Q AA zzg PP g −=−+ − γγ ( ) 2 2 2 2 1 2 2 2 1 21 21 22 Q AA AA zzg PP g − =−+ − γγ ( )21 21 2 2 2 1 2 2 2 12 22 zzg PP g AA AA Q −+ − − = γγ ( )21 21 2 2 2 1 21 22 zzg PP g AA AA Qth −+ − − = γγ Datum ( )21 21 2 2 2 1 21 22 zzg PP g AA AA CQ dact −+ − − = γγ D1,A1, P1, Z1,V1 D2,A2, P2, Z2,V2
- 6. Flow Measurements inPipes 6 Venturimeter thdact QcQ = ( )21 21 2 2 2 1 21 22 zzg PP g AA AA CQ dact −+ − − = γγ Since Where Cd is coefficient of discharge and is defined as ratio of actual discharge to theoretical discharge . Datum ( )21 21 2 2 2 1 21 22 zzg PP g AA AA CQ dact −+ − − = γγ D1,A1, P1, Z1,V1 D2,A2, P2, Z2,V2
- 7. Flow Measurements inPipes 7 Types ofVenturimeter a. HorizontalVenturimeter b.Vertical Venturimeter a. HorizontalVenturimeter Figure shows a venturimeter connected with a differential manometer. At section 1, diameter of pipe is D1, and pressure is P1 and similar D2 and P2 are respective values at section 2. h x y 1 2 According to gauge pressure equation γγ 21 P yhSx P m =+−− )()(21 hhSxyhS PP mm −=−−=− γγ − − = γγ 21 2 2 2 1 21 2 PP g AA AA CQ dact
- 8. Flow Measurements inPipes 8 Types ofVenturimeter a. HorizontalVenturimeter b.Vertical Venturimeter a. HorizontalVenturimeter h x y 1 2 γγ 21 P yhSx P m =+−− )()(21 hhSxyhS PP mm −=−−=− γγ ( )21 21 2 2 2 1 21 22 zzg PP g AA AA CQ dact −+ − − = γγ ( ) 021 =− zz )()(21 hhSxyhS PP mm −=−−=− γγ − − = γγ 21 2 2 2 1 21 2 PP g AA AA CQ dact For horizontal venturimeter, − − = γγ 21 2 2 2 1 21 2 PP g AA AA CQ dact According to gauge pressure equation
- 9. Flow Measurements inPipes 9 Types ofVenturimeter a. HorizontalVenturimeter b.Vertical Venturimeter b.VerticalVenturimeter Figure shows a venturimeter connected with a differential manometer. h x y 1 hzhS PP xyhS PP P yhSx P m m m −∆+=− −+=− =−−+ γγ γγ γγ 21 21 21 Datum ∆z yhzx +=∆+Q ( )21 21 2 2 2 1 21 22 zzg PP g AA AA CQ dact −+ − − = γγ According to gauge pressure equation
- 10. Flow Measurements inPipes 10 Types ofVenturimeter a. HorizontalVenturimeter b.Vertical Venturimeter b.VerticalVenturimeter hzhS PP m −∆+=− γγ 21 h x y 1 Datum ∆z yhzx +=∆+Q ( )21 21 2 2 2 1 21 22 zzg PP g AA AA CQ dact −+ − − = γγ ( )21 21 2 2 2 1 21 22 zzg PP g AA AA CQ dact −+ − − = γγ ( ) zzz ∆=− 21
- 11. Numerical Problem 11 Find theflow rate in venturimeter as shown in figure if the mercury manometer reads h=10cm. The pipe diameter is 20cm and throat diameter is 10 cm and ∆z =0.45m. Assume Cd=0.98 and direction of flow is downward. h x y 1 Datum ∆z yhzx +=∆+Q hzhS PP m −∆+=− γγ 21 ( )21 21 2 2 2 1 21 22 zzg PP g AA AA CQ dact −+ − − = γγ
- 12. Orifice 12 An orifice isan opening (usually circular) in wall of a tank or in plate normal to the axis of pipe, the plate being either at the end of the pipe or in some intermediate location. An orifice is characterized by the fact that the thickness of the wall or plate is very small relative to the size of opening.
- 13. Orifice 13 A standard orificeis one with a sharp edge as in Fig (a) or an absolutely square shoulder (Fig. b) so that there in only a line contact with the fluid Those shown in Fig. c and d are not standard because the flow through them is affected by the thickness of plate, the roughness of surface and radius of curvature (Fig. d). Hence such orifices should be calibrated if high accuracy is desired.
- 14. Classification of Orifice 14 Accordingto size 1. Small orifice 2. Large orifice An orifice is termed as small when its size is small compared to head causing flow.The velocity does not vary appreciably from top to bottom edge of the orifice and is assumed to be uniform. The orifice is large if the dimensions are comparable with the head causing flow.The variation in the velocity from top to bottom edge is considerable. According to shape 1. Circular orifice 2. Rectangular orifice 3. Square orifice 4.Triangular orifice According to shape of upstream edge 1. Sharp-edged orifice 2. bell-mouthed orifice According to discharge condition 1. Free discharge orifice 2. Submerged orifice
- 15. Coefficients 15 Coefficient of contraction:It is the ratio of area Ac of jet, to the area Ao of the orifice or other opening. Coefficient of velocity: It is ratio of actual velocity to ideal velocity Coefficient of discharge: It is the ratio of actual discharge to ideal discharge. occ AAC /= th act v V V C = cv thth actact th act d CC AV AV Q Q C === Vena-Contracta is section of jet of minimum area.This section is about 0.5Do from upstream edge of the opening, where Do is diameter of orifice
- 16. Orifice 16 Small orifice Figure showsa tank having small orifice at it bottom. Let the flow in tanks is steady. Let’s take section 1 (at the surface) and 2 just outside of tank near orifice. According to Bernoulli’s equation Datum Z1 Z2 Outflow inflow Cross- sectional area 1 2 g v z P g v z P 22 2 2 2 2 2 1 1 1 ++=++ γγ g v zz 2 000 2 2 21 ++=++ H gHv Hzz g v th 2 2 21 2 2 = =−= Where, H is depth of water above orifice
- 17. Orifice 17 Small orifice Datum Z1 Z2 Outflow inflow Cross-sectional area,A 1 2 H gHvth 2=Q Where,A is cross-sectional are of orifice and Cd is coefficient of discharge. gHACAvCQ gHAAvQ dthdact thth 2 2 == ==
- 18. Mouthpieces/tubes 18 A tube/mouth pieceis a short pipe whose length is not more than two or three diameters. There is no sharp distinction between a tube and a thick walled orifices. A tube may be uniform diameter or it may diverge. Figure: types and coefficients of tubes/mouthpieces
- 19. Nozzle 19 Figure shows anozzle. At section 1, diameter of pipe is D1, and pressure is P1 and similar D2 and P2 are respective values at section 2. 1 2 g v g vP 2 00 2 0 2 2 2 11 ++=++ γ γ 1 2 1 2 2 22 P g v g v =− A nozzle is a tube of changing diameter, usually converging as shown in figure if used for liquids. 2211 21 VAVAQ QQQ == == According to continuity eq. γ 1 2 1 2 2 2 2 2 P g A Q A Q =− g v z P g v z P 22 2 2 2 2 2 1 1 1 ++=++ γγ
- 20. Nozzle 20 1 2 Jet: Itis a stream issuing from a orifice, nozzle, or tube. 2211 21 VAVAQ QQQ == == According to continuity eq. γ 1 2 1 2 2 2 2 2 P g A Q A Q =− γ γ 1 2 2 2 1 21 1 2 1 2 2 2 2 2 11 P g AA AA Q P g AA Q th − = = − γ 1 2 2 2 1 21 2 P g AA AA CQ dact − = Jet
- 21. Nozzle 21 1 2 γ 1 2 2 2 1 21 2 P g AA AA CQ dact − = Ao=cross-section area at nozzle ( ) ( ) γ 1 222 1 1 2 P g ACA ACA CQ oc oc dact − = oc ACA =2 ( ) ( ) − = = 222 1 1 1 2 oc oc d act ACA ACA CK P gKQ γ Where, K is coefficient of nozzle Vena-contracta is section of jet of minimum area.This section is about 0.5Do from upstream edge of the opening, where Do is diameter of orifice Pressure, P1 is then measured with the help of piezometer or manometer
- 22. Nozzle 22 1 2 h hSx P hSx P m m += =−− γ γ 1 1 0 According togauge pressure equation
- 23. Calibration and CalibrationCurves 23 Calibration : Determine coefficients of flow measuring devices, e.g., Cd, Cc, Cv, etc Calibration curve: Plotting calibration curve e.g., h1/2 Vs Qact h3/2 Vs Qact
- 24. Numerical Problems 24 Discharge andheadloss in nozzle are 20L/s and 0.5m respectively. If dia of pipe is 10cm and dia of nozzle is 4cm, determine the manometric reading. Manometric fluid is mercury. 1 2 h LH g v z P g v z P +++=++ 22 2 2 2 2 2 1 1 1 γγ hSx P m+= γ 1 Solution: γ 1 2 2 2 1 21 2 P g AA AA CQ dact − = 5cm
- 25. Numerical Problem 25 A jetdischarges from an orifice in a vertical plane under a head of 3.65m. The diameter of orifice is 3.75 cm and measured discharge is 6m3/s.The co- ordinates of centerline of jet are 3.46m horizontally from the vena- contracta and 0.9m below the center of orifice. Find the coefficient of discharge, velocity and contraction. ( )gHAQC gHACAvCQ actd dthdact 2/ 2 = == gH y gx v v C th act v 2 2 2 == vdc CCC /= Outflow inflow 1 2 H x=3.46m y=0.9m tvx act= 2 2 1 gty = ygxVact 2/2 =
- 26. Bernoulli’s Equation 26 Static Pressure: Dynamic pressure : Hydrostatic Pressure: Stagnation Pressure: Static pressure + dynamic Pressure H g V z P =++ 2 2 γ HeadTotalheadVelocityheadElevationheadPressure =++ P gZρ 2/2 Vρ contt V gzP =++ 2 2 ρρ Multiplying with unit weight,γ, stagP V P =+ 2 2 ρ
- 27. Pitot Tube andPitot Static Tube 27 Pitot Tube: It measures sum of velocity head and pressure head Piezoemeter: It measures pressure head Pitot-Static tube: It is combination of piezometer and pitot tube. It can measure velocity head.
- 28. Pitot Tube andPitot Static Tube 28 V Consider the following closed channel flow (neglect friction): Uniform velocity profile z1 2 g V 2 P 2 + γ γ P open open piezometer tube Pitot tube g V 2 2 Pitot static tube γγ PP g V g V − += 22 22 γγ ρ stag stag P g VP P V P =+ =+ 2 2 2 2 Remember !! −= γγ PP gV stag th 2 Stagnation point Theoretical/ideal flow velocity at elevation z in pipe.
- 29. Pitot Static Tube 29 Inreality, directional velocity fluctuations increase pitot-tube readings so that we must multiply Vth with factor C varying from 0.98 to 0.995 to give true (actual) velocity −= γγ PP gCV stag act 2 However, piezometer holes are rarely located in precisely correct position to indicate true value of P/γ, we modify above equation as; Where C1 is coefficient of instrument to account for discrepancy. −= γγ PP gCV stag act 21
- 30.
- 31.
- 32. Notches and Weirs 32 Notch.A notch may be defined as an opening in the side of a tank or vessel such that the liquid surface in the tank is below the top edge of the opening. A notch may be regarded as an orifice with the water surface below its upper edge. It is generally made of metallic plate. It is used for measuring the rate of flow of a liquid through a small channel of tank. Weir: It may be defined as any regular obstruction in an open stream over which the flow takes place. It is made of masonry or concrete.The condition of flow, in the case of a weir are practically same as those of a rectangular notch. Nappe: The sheet of water flowing through a notch or over a weir Sill or crest. The top of the weir over which the water flows is known as sill or crest. Note:The main difference between notch and weir is that the notch is smaller in size compared to weir.
- 33. Classification of Notches/Weirs 33 Classificationof Notches 1. Rectangular notch 2.Triangular notch 3.Trapezoidal Notch 4. Stepped notch Classification ofWeirs According to shape 1. Rectangular weir 2. Cippoletti weir According to nature of discharge 1. Ordinary weir 2. Submerged weir According to width of weir 1. Narrow crested weir 2. Broad crested weir According to nature of crest 1. Sharp crested weir 2. Ogee weir
- 34. Discharge over RectangularNotch/Weir 34 Consider a rectangular notch or weir provided in channel carrying water as shown in figure. In order to obtain discharge over whole area we must integrate above equation from h=0 to h=H, therefore; Figure: Flow over rectangular notch/weir 2/3 2 3 2 LHgCQ dact = Note:The expression of discharge (Q) for rectangular weir and sharp crested weirs are same.
- 35. Numerical Problems 35 A rectangularnotch 2m wide has a constant head of 500mm. Find the discharge over the notch if coefficient of discharge for the notch is 0.62.
- 36. Numerical Problems 36 A rectangularnotch has a discharge of 0.24m3/s, when head of water is 800mm. Find the length of notch.Assume Cd=0.6
- 37. Discharge over TriangularNotch (V-Notch) 37 In order to obtain discharge over whole area we must integrate above equation from h=0 to h=H, therefore; ( )[ ]2/5 2/tan2 15 8 HgCQ dact θ=
- 38. Numerical Problems 38 Find thedischarge over a triangular notch of angle 60o, when head over triangular notch is 0.2m.Assume Cd=0.6
- 39. Numerical Problems 39 During anexperiment in a laboratory, 0.05m3 of water flowing over a right angled notch was collected in one minute. If the head over sill is 50mm calculate the coefficient of discharge of notch. Solution: Discharge=0.05m3/min=0.000833m3/s Angle of notch, θ=90o Head of water=H=50mm=0.05m Cd=?
- 40. Numerical Problems 40 A rectangularchannel 1.5m wide has a discharge of 0.2m3/s, which is measured in right-angledV notch, Find position of the apex of the notch from the bed of the channel. Maximum depth of water is not to exceed 1m. Assume Cd=0.62 Width of rectangular channel, L=1.5m Discharge=Q=0.2m3/s Depth of water in channel=1m Coefficient of discharge=0.62 Angle of notch= 90o Height of apex of notch from bed=Depth of water in channel-height of water overV-notch =1-0.45= 0.55m
- 41. Thank you Questions…. Feel freeto contact: 41
- 42. Discharge over RectangularNotch/Weir 42 Consider a rectangular notch or weir provided in channel carrying water as shown in figure. Figure: flow over rectangular notch/weir H=height of water above crest of notch/weir P =height of notch/weir L =length of notch/weir dh=height of strip h= height of liquid above strip L(dh)=area of strip Vo = Approach velocity Theoretical velocity of strip neglecting approach velocity = Thus, discharge passing through strips = gh2 velocityArea×
- 43. Discharge over RectangularNotch/Weir 43 Where, Cd = Coefficient of discharge LdhA ghv strip strip = = 2 ( )ghLdhdQ 2= Therefore, discharge of strip In order to obtain discharge over whole area we must integrate above eq. from h=0 to h=H, therefore; 2/3 0 2 3 2 2 LHgQ dhhLgQ H = = ∫ 2/3 2 3 2 LHgCQ dact = Note:The expression of discharge (Q) for rectangular weir and sharp crested weirs are same.
- 44. Discharge over TriangularNotch (V-Notch) 44 In order to obtain discharge over whole area we must integrate above equation from h=0 to h=H, therefore; ( ) ( )( )( ) ( ) ( ) dhhhHgQ ghhHdhQ H H ∫ ∫ −= −= 0 0 2/tan22 22/tan2 θ θ ( ) ( ) ( ) = −= ∫ 2/5 0 2/32/1 15 4 2/tan22 2/tan22 HgQ dhhHhgQ H θ θ ( )[ ]2/5 2/tan2 15 8 HgQ θ= ( )[ ]2/5 2/tan2 15 8 HgCQ dact θ=
- 45. Discharge over TrapezoidalNotch 45 Assignment for you.