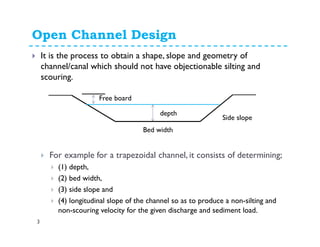
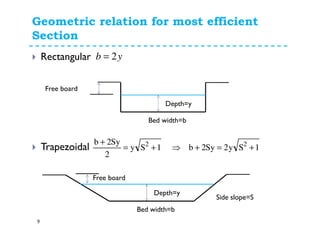
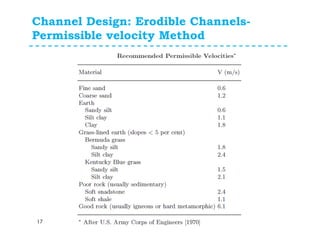
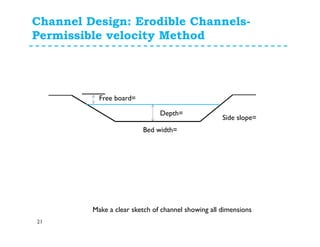
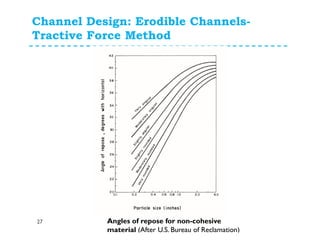
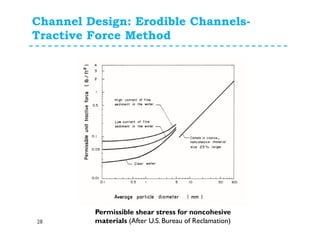
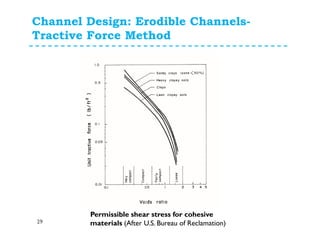
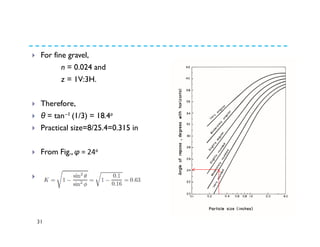
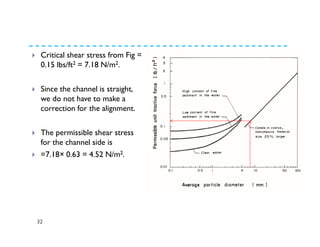
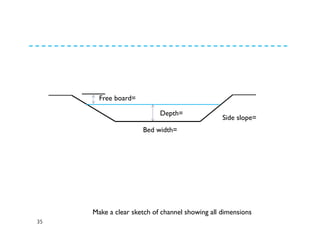
The document discusses open channel design for both rigid boundary and erodible channels. It describes the key steps in designing trapezoidal channels including determining depth, bed width, side slopes, and longitudinal slope. For rigid boundary channels, the most common design approach is to use Manning's equation to select dimensions that produce non-silting, non-scouring velocities. For erodible channels, two common methods are discussed: the permissible velocity method, which ensures the mean flow velocity is below erosion thresholds; and the tractive force method, which involves equating tractive forces to critical shear stresses of the channel material.

1. CHAPTER 3: OPEN CHANNEL DESIGN
Dr. Mohsin Siddique
Assistant Professor
1
0401544-HYDRAULIC STRUCTURES
University of Sharjah
Dept. of Civil and Env. Engg.

2. Learning Outcome of Today’s Lecture
2
After completing this lecture…
The students should be able to:
Understand the concepts of open channel design
Learn about various method applied in open channel design
Design open channel section for both rigid boundary and
erodible conditions

3. Open Channel Design
3
It is the process to obtain a shape, slope and geometry of
channel/canal which should not have objectionable silting and
scouring.
For example for a trapezoidal channel, it consists of determining;
(1) depth,
(2) bed width,
(3) side slope and
(4) longitudinal slope of the channel so as to produce a non-silting and
non-scouring velocity for the given discharge and sediment load.
depth
Bed width
Side slope
Free board

4. Open Channel Design: Channel types
4
Types of channels based on material
Lined channels (Rigid boundary channels)
Unlined channels (erodible or earthen channels)
Types of channels based on shape
Circular channel
Triangular channel
Rectangular channel
Trapezoidal channel

5. Open Channel Design: Free Board
5
Free board is vertical distance between the design water surface and the
top of the channel bank. It is provided to account for uncertainty in design,
construction, and operation of the channel.
The US Bureau of Reclamation recommends a minimum freeboard of 0.3m
(1ft) for small channels and the following formula for estimating the
freeboard (FB) for larger channels
Where y is depth of channel in m (ft) and C is coefficient which varies from
0.7 (1.2) for small channels with capacity of 0.6 m3/s (20 ft3/s) to 0.9 (1.6)
for larger channels with a capacity of 85m3/s (3000 ft3/s) or greater
Sometime additional freeboard is required at out edge of curved section
due to centrifugal force.
yCFB =

6. Channel Design: Rigid Boundary-Rectangular
Channels
6
In rigid channels a layer of rigid material (e.g., Concrete, bricks and stone
etc) is used at the periphery of channel to reduce seepage, to increase
discharge capacity and prevent erosion.
Dimension of rectangular channels are based on most efficient rectangular
section. i.e (b=2y or y=b/2) where b and y are width and depths of channel
respectively.
For trapezoidal channels, side slopes varies from 1:1 for small channels to
1.5(H):1(v) for large channels.
These channels can be used for both subcritical and supercritical flows.
The design if primarily based on Manning’s Equation
Where Q is discharge, n is roughness coefficient, A is area of flow, R is
hydraulic radius, So is channel bed slope, and Co is coefficient (1 for SI unit
and 1.49 for U.S. customary units)
( )2/13/22/13/2
/ ooo
o
SCnQARSAR
n
C
Q =⇒=

7. 7 Ref: Open channel hydraulics byVen Te Chow

8. Channel Design: Rigid Boundary Channels
8
Design Procedure:
1. Select a value of roughness coefficient ,n, and bottom slope, So, for the
flow surface
2. Compute section factor from AR2/3 = nQ/(CoSo0.5),
3. Determine the channel dimensions and the flow depth for which AR2/3 is
equal to the value determined in step 2. For example, for a trapezoidal
section, select a value for the side slope, z, and compute several different
ratios of bottom width Bo and flow depth y for which AR2/3 is equal to that
determined in step 2. Select a ratio Bo/y that gives a cross section near to
the best hydraulic section
4. Check that the minimum velocity is not less than that required to carry
the sediment to prevent silting.
5.Add a suitable amount of freeboard.
6. Make a sketch providing all the dimensions.

9. Geometric relation for most efficient
Section
9
Rectangular
Trapezoidal 1Sy2Sy2b1Sy
2
Sy2b 22
+=+⇒+=
+
yb 2=
Depth=y
Bed width=b
Side slope=S
Free board
Depth=y
Bed width=b
Free board

10. Channel Design: Rigid Boundary
Channels
10
Example: Design a trapezoidal channel to carry a discharge of 10 m3/s.The
channel will be excavated through rock by blasting.The topography in the area is
such that a bottom slope of 1 in 4000 will be suitable.
Solution: For the blasted rock surface, n = 0.030 and let us select a value
for the side slope, Z, as 1 horizontal to 4 vertical.The substitution of these
values into the Manning equation yields
yB
yyB
ZyB
Z
o
o
o
56.1
)25.0(2125.02
21Zy2
1Zy2y2B
2
2
2
o
=
−+=
−+=
+=+
( )
( )
y
y
y
P
A
R
yyyyBP
yyyyyyBA
o
o
495.0
66.3
81.1
66.306.256.114/12
81.125.056.1)
4
1
(
2
2
2
===
=+=−+=
=+=+=
my
y
yy
AR
72.2
97.1831.1
97.18)495.0(81.1
97.18
67.2
3/22
3/2
=
=
=
=

11. Channel Design: Rigid Boundary
Channels
11
Solving this equation for y, we get
y = 2.72 m.
Then, Bo = 1.56×2.72 = 4.24m.
Based on Eq. of Freeboard,
FB =0.8 × (2.72)0.5 = 1.32m.
Therefore, total depth = 2.72 + 1.32 = 4.04 =4.05 m.
The flow area for a flow depth of 2.72 m is 13.31 m2.
Therefore, the flow velocity = 10/13.31 = 0.75m/s
Froude No. =V/(gy)0.5=0.75/(9.81*2.72)0.5=0.14

12. Channel Design: Rigid Boundary
Channels
12
Make a clear sketch of channel showing all dimensions
Depth=
Bed width=
Side slope=
Free board=

13. Channel Design: Erodible Channels
13
If the channel bottom or sides are erodible, then the design requires that
the channel size and bottom slope are selected so that channel is not
eroded.
Erodible channels are designed for subcritical flow conditions with value of
Froude number less than 1.
A trapezoidal channel section is usually used for erodible channels.To
design these channels, first an appropriate value for the side slope is
elected so that the sides are stable under all conditions.

14. Basic Definitions
Froude’s Number (FN)
It is the ratio of inertial forces to
gravitational forces.
For a rectangular channel it may be
written as
FN= 1 Critical Flow
> 1 Super-Critical Flow
< 1 Sub-Critical Flow
gy
V
NF =
William Froude (1810-79)
Born in England and engaged
in shipbuilding. In his sixties
started the study of ship
resistance, building a boat
testing pool (approximately 75
m long) near his home. After his
death, this study was continued
by his son, Robert Edmund
Froude (1846-1924). For
similarity under conditions of
inertial and gravitational forces,
the non-dimensional number
used carries his name.
14

15. Channel Design: Erodible Channels
15
There are many method available but the following two methods are
discussed here.
Permissible velocity method and
Tractive force method.

16. Channel Design: Erodible Channels-
Permissible velocity Method
16
PermissibleVelocity Method
In permissible velocity method, channel size is selected such that mean flow
velocity for design discharge under uniform flow conditions is less than
permissible velocity.
Permissible Velocity is defined as the mean velocity at or below which
bottom and sides of channels are not eroded.
Permissible velocity depends upon:
Type of soil
Size of particles
Depth of flow
Curvature of channel

17. Channel Design: Erodible Channels-
Permissible velocity Method
17

18. Channel Design: Erodible Channels-
Permissible velocity Method
18
Design Procedure:
1. For the specified material, select value of n, side slope, z, the permissible
velocity, V, (fromTables).
2. Determine the required hydraulic radius, R, from Manning formula, and
the required flow area, A, from the continuity equation, A = Q/V.
3. Compute the wetted perimeter, P = A/R.
4. Determine the channel bottom width, Bo, and the flow depth, y, for which
the flow area A is equal to that computed in step 2 and the wetted
perimeter, P, is equal to that computed in step 3.
5. Add a suitable value for the freeboard.
6. Make a sketch providing all the dimensions.
( )
2
12 zyBP
yzyBA
o
o
++=
+=

19. Channel Design: Erodible Channels-
Permissible velocity Method
19
Design a channel to carry a flow of 6.91 m3/s.The channel will be excavated
through stiff clay at a channel bottom slope of 0.00318.
Solution:
For stiff clay, n = 0.025, suggested side slope, z = 1 : 1 (fromTable ), and the
permissible flow velocity (fromTable ) is 1.8 m/s.
Hence,
A = Q/V=6.91/1.8 = 3.83 m2
Substituting values for V, n, and So into Manning equation,
and solving for R, we get R = 0.713 m. Hence,
P = A/R=3.83/0.713= 5.37m
2/13/2
o
o
SAR
n
C
Q =

20. Channel Design: Erodible Channels-
Permissible velocity Method
20
Substitution into expressions for P and A and equating them to the values
computed above, we obtain
Eliminating Bo from these equations yields
Solution of above quadratic equation yields y=1.22m and hence Bo=1.9m
Freeboard (FB)=0.8x(1.22)0.5=0.99
Total depth of channel section=1.22+0.99=2.21m
( ) ( )
yByB
yyByyB
oo
oo
83.211237.5
.183.3
2
+=++=
+=+=
083.337.583.1 2
=+− yy

21. Channel Design: Erodible Channels-
Permissible velocity Method
21
Make a clear sketch of channel showing all dimensions
Depth=
Bed width=
Side slope=
Free board=

22. Channel Design: Erodible Channels-
Permissible velocity Method
22
Problem: A grass-lined drainage channel is to carry a discharge of 2000 cfs
at a maximum velocity of 4.0 fps.The side slopes of the channel will be 4:1
and the longitudinal slope of the channel will be 0.001. Design the channel
for Manning’s n values of 0.03 and 0.035.
Answer: for n=0.03, y=4.9ft, Bo=83ft and FB=3.1ft
for n=0.035, y=7.7ft, Bo=34.2ft and FB=3.9ft

23. Channel Design: Erodible Channels-
Tractive Force Method
23
Tractive Force Method
Scour and erosion process can be viewed in rational way by considering
forces acting on particles lying on channel bottom or sides.
The channel is eroded if resultant of forces tending to move particles is
greater than resultant of forces resisting motion. This concept is referred as
tractive force approach.
Tractive Force
The force exerted by flowing water on bottom and sides of channel is
called tractive force. In uniform flow, this force is equal to component of
weight acting in direction of flow and is given by
ooo ySRS γγτ ==

24. Channel Design: Erodible Channels-
Tractive Force Method
24
CriticalTractive Force
The force at which channel material begins to move from stationery
condition is called critical tractive force.
Distribution ofTractive Force
Distribution of tractive force or shear stress over channel perimeter is not
uniform. For trapezoidal channels, unit tractive force at channel bottom
may be assumed equal to (γ y So) and at channel sides equal to 0.76 γ y So
Reduction Factor for Channel Sides
Reduction factor (tractive force ratio) for critical tractive force on channel
sides is:
i.e K=Permissible Tractive force on side slope/Critical Tractive
force

25. Channel Design: Erodible Channels-
Tractive Force Method
25
Effect of angle of repose should be considered only for coarse non
cohesive materials and can be neglected for fine cohesive materials.
Critical shear stress for cohesive and non cohesive materials is given in the
figures on next slides.These values are for straight channels and should be
reduced for sinuous channels as below:
Slightly sinuous channels = 10%
Moderately sinuous channels = 25%
Highly sinuous channels = 40%

26. Basic Definitions
Channel classification
26
Straight Channel
Braided Channel
Meandering Channel
Sinuosity is ratio of actual path length
to shortest path length

27. Channel Design: Erodible Channels-
Tractive Force Method
27 Angles of repose for non-cohesive
material (After U.S. Bureau of Reclamation)

28. Channel Design: Erodible Channels-
Tractive Force Method
28
Permissible shear stress for noncohesive
materials (After U.S. Bureau of Reclamation)

29. Channel Design: Erodible Channels-
Tractive Force Method
29
Permissible shear stress for cohesive
materials (After U.S. Bureau of Reclamation)

30. Channel Design: Erodible Channels-
Tractive Force Method
30
Example: Design a straight trapezoidal channel for a design discharge of
10 m3/s.The bottom slope is 0.00025 and the channel is excavated through
fine gravel having particle size of 8 mm.Assume the particles are
moderately rounded and the water carries fine sediment at low
concentrations.
Solution:
Q = 10 m3/s;
So = 0.00025;
Material: Fine gravel, moderately rounded; and
Particle size = 8 mm.
Determine: Bo = ? And Flow depth, y = ?

31. 31
For fine gravel,
n = 0.024 and
z = 1V:3H.
Therefore,
θ = tan−1 (1/3) = 18.4o
Practical size=8/25.4=0.315 in
From Fig., φ = 24o
Hence,

32. 32
Critical shear stress from Fig =
0.15 lbs/ft2 = 7.18 N/m2.
Since the channel is straight,
we do not have to make a
correction for the alignment.
The permissible shear stress
for the channel side is
=7.18× 0.63 = 4.52 N/m2.

33. 33
Now, the unit tractive force on the side = 0.76γySo
= 0.76×999×9.81y×0.00025
= 1.862y
By equating the unit tractive force to the permissible stress, we obtain
1.862y = 4.52
Or y = 2.43m
The channel bottom width, Bo, needed to carry 10 m3/s may be determined
from the Mannings’ equation
( ) ( ) QS
yzB
yzyB
yzyB
n
QSAR
n
o
o
o =








++
+
+
=
0
3/2
2
0
3/2
12
1
1

34. 34
By substituting n = 0.024, z = 3, y = 2.43, So = 0.00025, and Q = 10 m3/s, and
solving for Bo, we obtain Bo = 8.24m
Free Board, FB, = 0.8 × (2.43)0.5 = 1.40 m.
For a selected freeboard of 1.4 m, the depth of section = 2.43 + 1.4 = 3.82
m.
For ease of construction, select a bottom width, Bo = 8.25 m.

35. 35
Make a clear sketch of channel showing all dimensions
Depth=
Bed width=
Side slope=
Free board=

36. Thank you
Questions….
36