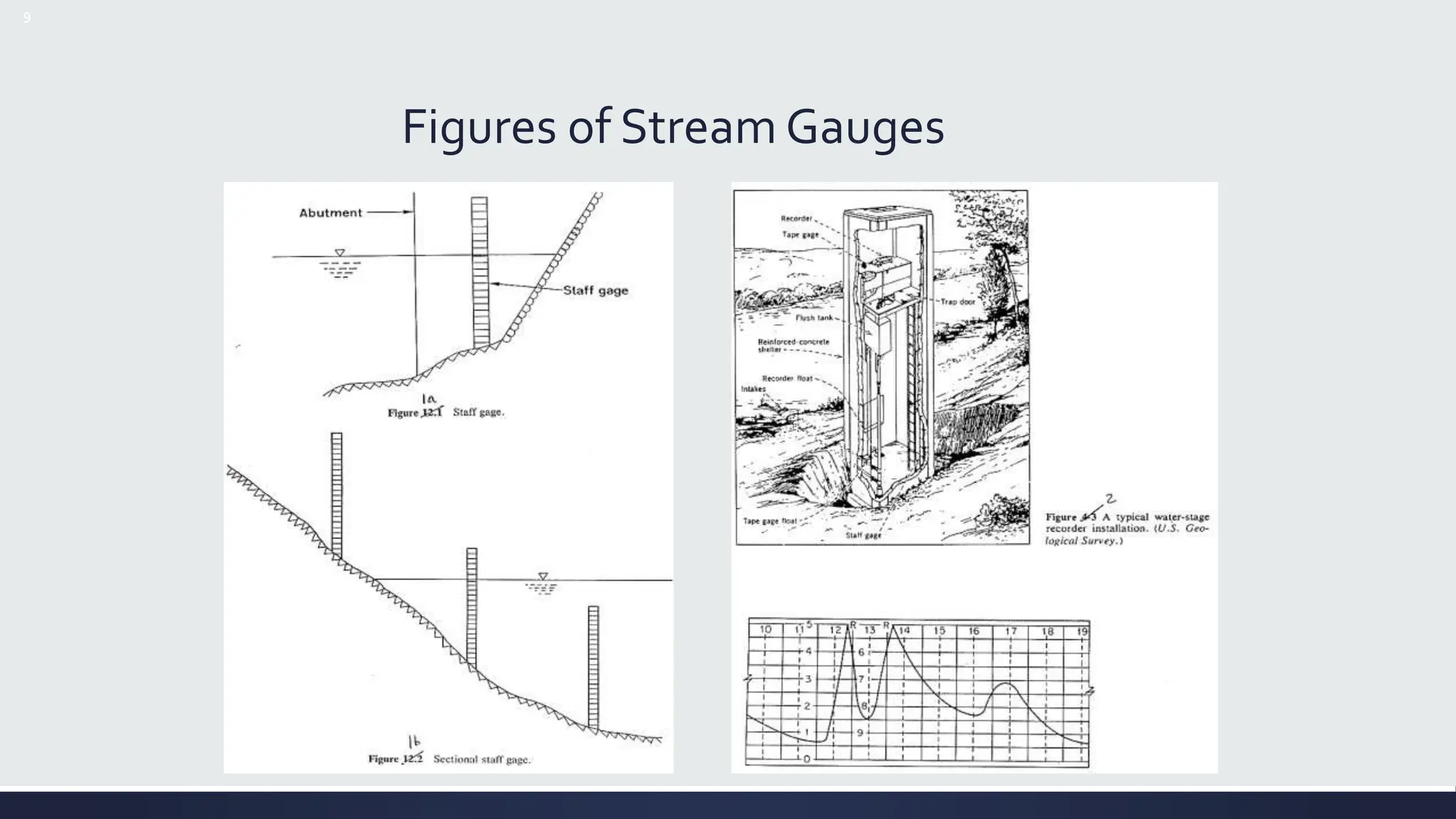
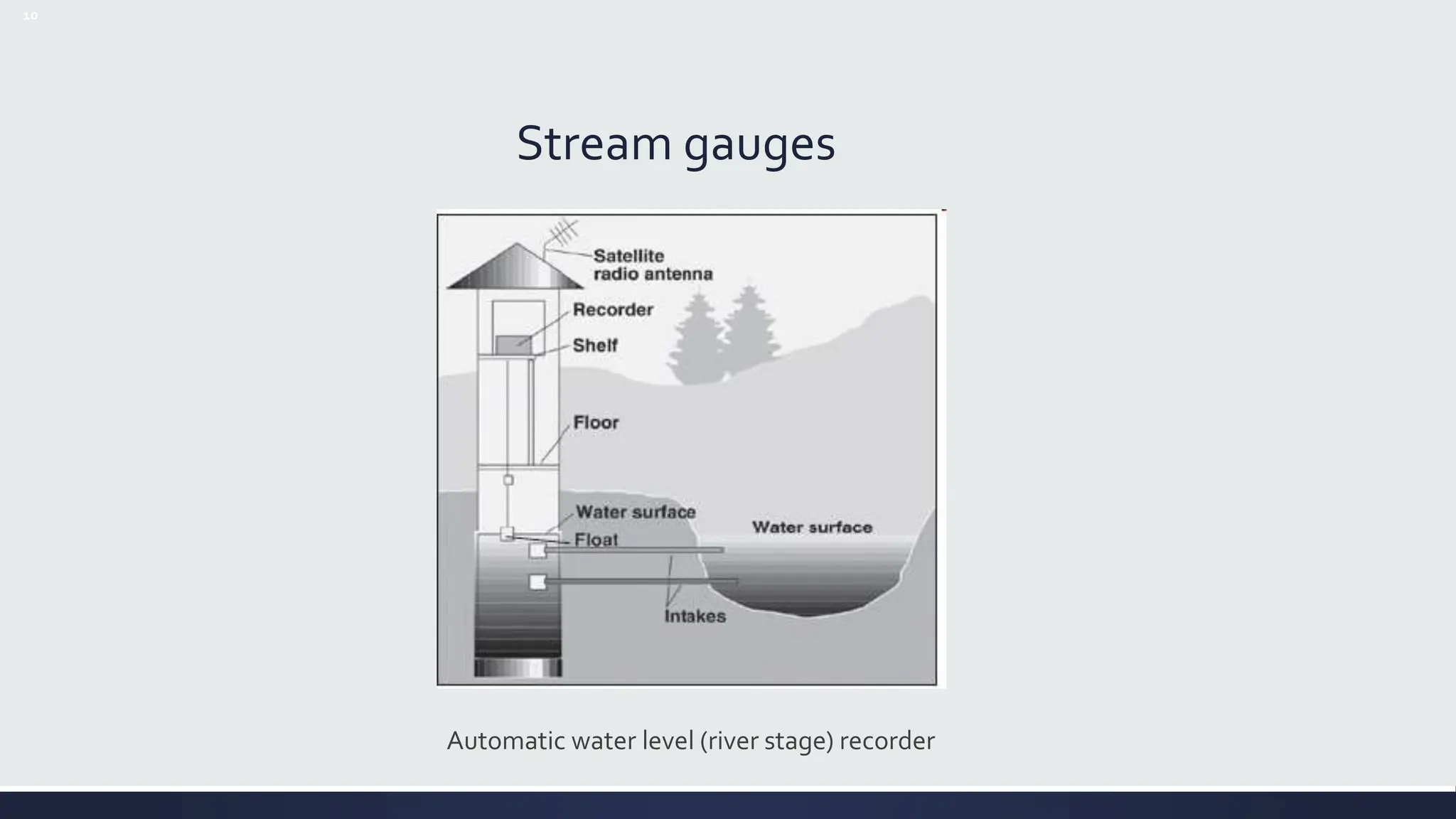
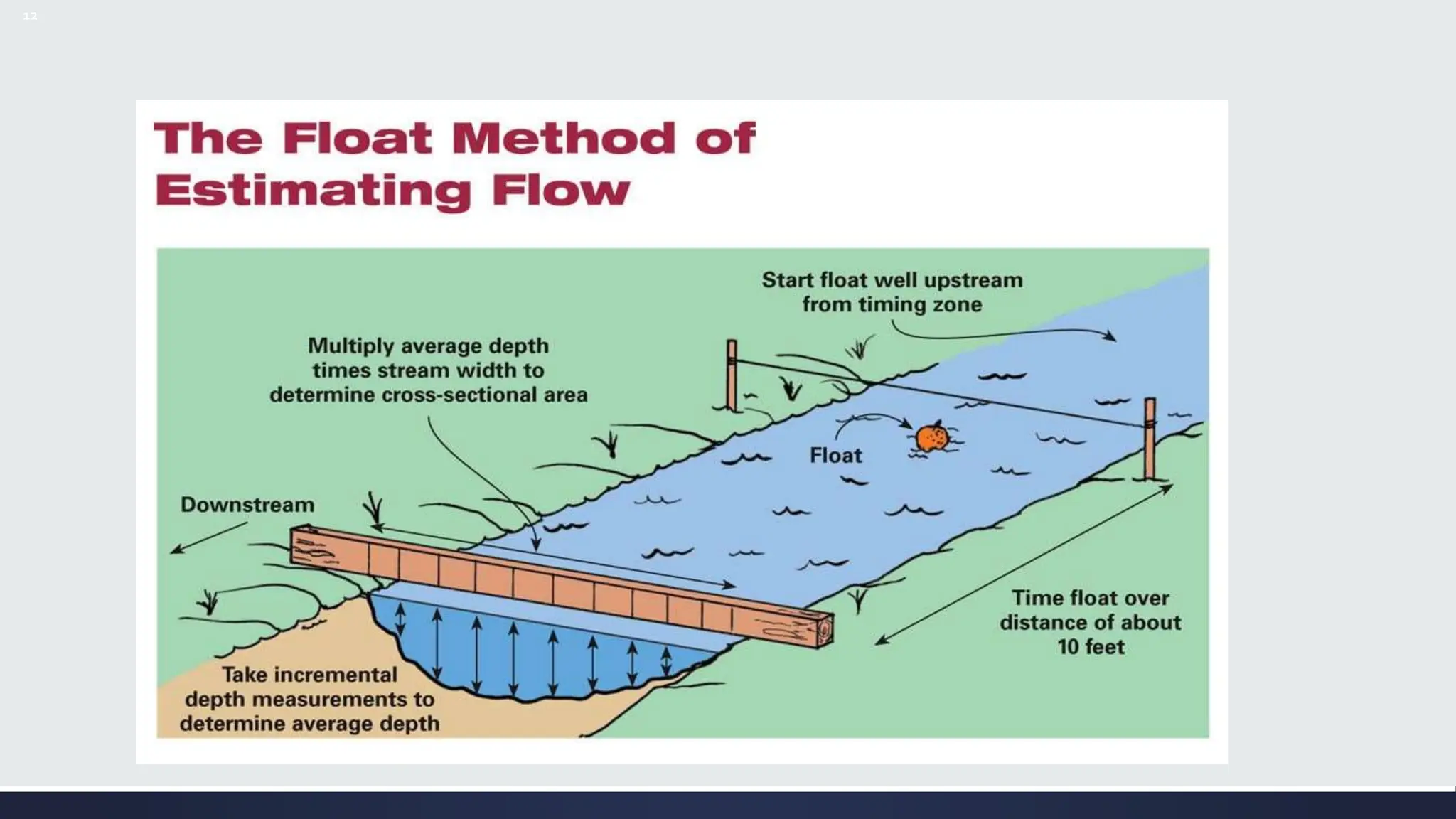
The document discusses streamflow measurement techniques essential for engineering hydrology, emphasizing their significance in water supply, flood control, and reservoir design. It covers methods of discharge measurement, including direct and indirect techniques, the use of gauges, and various equations for calculating flow velocity and discharge. Additionally, it highlights the importance of understanding channel features and the challenges associated with measuring in varying conditions.

1. STREAMFLOW
MEASUREMENT
Mrs Siti Kamariah Bt Md Sa’at
Faculty of Mechanical Engineering & Technology
UniMAP
MMJ24203
HYDROLOGY AND WATER RESOURCES ENGINEERING

2. 2
STREAMFLOW MEASUREMENT
TECHNIQUE

3. 3
Streamflow and Measurement
▪ The character, amount, and timing of discharge from a basin tells a lot about flow
paths within the basin.
▪ Stream flow is one of the most important topics in engineering hydrology because
it directly relates to water supply, flood control, reservoir design, navigation,
irrigation, drainage, water quality, and others.

4. 4
Need for Stream flow Measurements
▪ Floodplain management
▪ Flood forecasting & analysis
▪ Reservoir operations
▪ Low flows – water quality concerns
▪ Design structures – culverts, bridges, stormwater systems
▪ Evaluate changes in land use on watersheds and/or changes in
climatic regimes

5. 5
Need for Streamflow Measurements
▪ Important to hydrogeologist to identify how to create stream hydrographs from
discharge measurements

6. 6
Measurement of discharge
▪ Method used depends on type of study, size of river and flow, data
requirements, etc.
▪ Streamflow measurement techniques can be broadly classified into
2 categories:
▪ Direct determination – area-velocity method, dilution techniques,
electromagnetic method, ultrasonic method
▪ Indirect determination – hydraulic structures, slope-area method

7. 7
Streamflow Measurements
▪ Serves as the basis for many water resources engineering designs
▪ Three approaches
▪ Measurement of water stage (water level)
▪ Measurement of flow velocity
▪ Hydraulic Structure

8. 8
Streamflow Measurements
▪ Measurement ofWater Stage
▪ Water stage: the elevation above some arbitrary datum of water surface at a
station
▪ Types of Gages Measuring River Stage:
▪ Staff gage – vertical or inclined
▪ Suspended – weight gage
▪ Recording gage (automatic data logger)
▪ Crest – stage gage ( used to indicate high water mark)
▪ Pressure sensor
▪ Float

9. 9
Figures of Stream Gauges

10. 10
Stream gauges
Automatic water level (river stage) recorder

11. 11
FLOWVELOCITY MEASUREMENT
▪ Measurement of FlowVelocity
▪ Current meter
▪ Dilution technique
▪ Manning Equation
▪ Floats: Suitable for straight channel,
▪ V = L/T

12. 12

13. 13
Float method
▪ Floats are a simple way of measuring the
velocity of a stream, but they are not very
accurate.
▪ The surface velocity is obtained by
measuring the time (t secs) for a float to
travel a measured distance (L metres).
▪ It is best to choose a straight, uniform river
section about 30m long, and to time the
float over a number of repeated runs.

14. 14
Float method
▪ A factor of about 0.85 should be used to convert surface velocity to average velocity.
▪ Surface velocity (m/s) = L / t
▪ Average velocity (m/s) = 0.85 x L / t
▪ The cross section of the stream should be measured up carefully in a number of places along the
test distance, and the average cross-sectional area calculated (A sq m).
▪ Discharge (cubic metres per second)
= average velocity × cross sectional area of stream
= 0.85 × (L / t) × A
▪ Discharge (L/s) = 1000 × 0.85 × (L / t) × A

15. Discharge (Q) Measurement

16. 16
Area-Velocity
Method

17. 17
VELOCITY MEASUREMENT

18. 18
Measuring
Streamflow in small
streams with a
pygmy current meter

20. Discharge (Q) Measurement
Large rivers – from
bridges or moving
boats

22. 22
Current Meter Method
▪ 3 types of current meter
▪ Propeller type : for high discharge
▪ Price type using anemometer
▪ Electromagnetic type : for low river flow
▪ Rating curve for current meter is given by:
V = a + bN
whereV = flow velocity;
a = starting velocity to overcome
mechanical friction;
b = equipment calibration constant;
N = revolutions/sec.

23. 23
Current Meters

24. 24
For river velocity measurement, we need:
▪ Wading/Paddle
▪ Bridges
▪ Boat
▪ Cablecar
▪ Cableway

25. 25
Velocity-Area Method
▪ Mostly/frequently used
▪ River cross-section determined
▪ Velocity measured using
▪ Float (for straight channel)
▪ Current meter
▪ Vertical velocity measured at 0.2d and 0.8d if depth,d >0.6m. If d<0.6m,
velocity is measured at 0.6d m.

26. 26
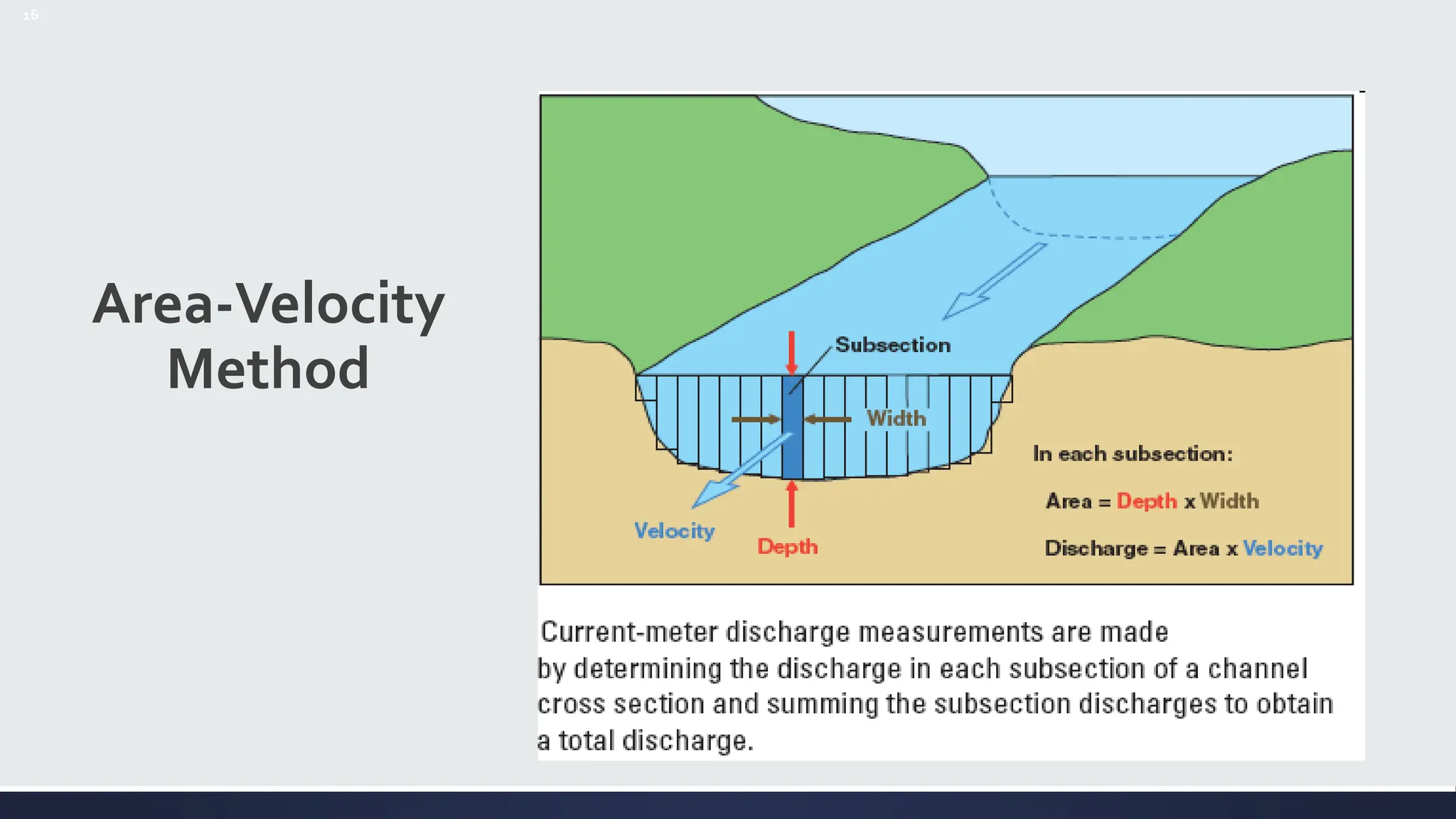
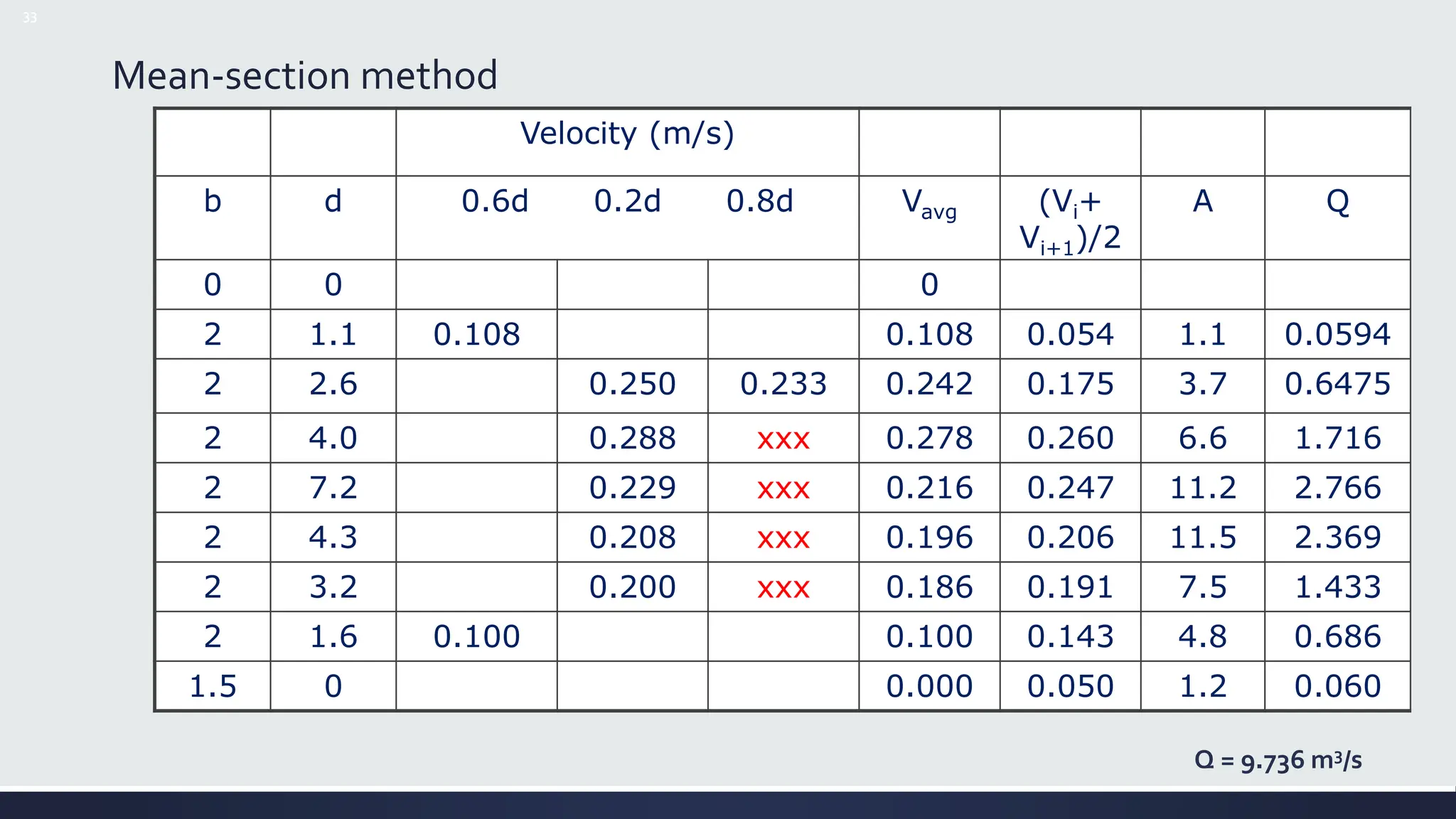
Velocity-Area Method
▪ Q = [Velocity x Area]
▪ Need to know width of channel (w), Depth of channel (d), andVelocity of flow (V) (ft/s or m/s)
▪ Area = w x d
▪ Because depth & velocity vary across a channel:
(1) Important to divide the channel into manageable segments (slices);Typically use 10-20
segments
(2) For each segment measure depth, width and velocity

27. 27
Measuring Streamflow Discharge
▪ Procedure: at each segment measure depth then velocity
▪ If Depth < 0.6m, take one reading @ 60% depth
▪ If Depth > 0.6m take 2 measurements and compute the average
▪ One @ 20% depth
▪ One @ 80% depth
▪ Average the two readings

28. 28
Measuring Streamflow Discharge
▪ Two method of measurement
▪ Mean section method
▪ Mid section method

29. 29
Mean-section Method
)
(
2
*
2
1
1
1










i
i
i
i
i
i
i
b
b
d
d
v
v
VA
q
Q
Computation of river discharge: Mean-Section Method
Principle: Using average value for each section

30. 30
Mid-section Method
 
i
i
i
i
i
d
v
b
b
q
Q
)
2
( 1
1 
 



Computation of river discharge: Mid-Section Method

31. 31
Example Calculation:
Find the Q for this case:
V = 0.25 N + 0.05
Where V= velocity (m/s)
N = number of revolution/s
a) Using mean-section method
b) Using mid-section method

32. 32
Example Calculation:
Distance
from edge, b
(m)
Depth, d
(m)
Rev/min
0.6d 0.2d 0.8d
0 0
2 1.1 14
4 2.6 48 44
6 4.0 57 52
8 7.2 43 37
10 4.3 38 32
12 3.2 36 29
14 1.6 12
15.5 0

33. 33
Mean-section method
Velocity (m/s)
b d 0.6d 0.2d 0.8d Vavg (Vi+
Vi+1)/2
A Q
0 0 0
2 1.1 0.108 0.108 0.054 1.1 0.0594
2 2.6 0.250 0.233 0.242 0.175 3.7 0.6475
2 4.0 0.288 xxx 0.278 0.260 6.6 1.716
2 7.2 0.229 xxx 0.216 0.247 11.2 2.766
2 4.3 0.208 xxx 0.196 0.206 11.5 2.369
2 3.2 0.200 xxx 0.186 0.191 7.5 1.433
2 1.6 0.100 0.100 0.143 4.8 0.686
1.5 0 0.000 0.050 1.2 0.060
Q = 9.736 m3/s

34. 34
Mid-section method
Velocity (m/s)
b d 0.6d 0.2d 0.8d Vavg (bi+1-
bi-1)/2
qi
0 0 0
2 1.1 0.108 0.108 2 0.238
4 2.6 0.250 0.233 0.242 2 1.258
6 4.0 0.288 x 0.278 2 2.224
8 7.2 0.229 x 0.216 2 3.110
10 4.3 0.208 x 0.196 2 1.685
12 3.2 0.200 x 0.186 2 1.190
14 1.6 0.100 0.100 1.75 0.280
15.5 0 0.000
Q = 9.986 m3/s

35. 35
Exercise
Calculate the discharge of the river gauging record shown inTable below
using mean and Mid section method.
Answer:
Mean section:Total Q= 20.52 m3/s
Mid-section:Total Q = 19.89 m3/s

36. 36
Dilution gauging
▪ Using tracer/chemical at upstream
▪ For uneven stream base, good method for turbulent streams
▪ Applying mass conservation principle
▪ Q can be determined by tracer quantity and concentration at upstream and downstream
(after dilution) using mass transfer equation.
▪ need to use tracer that is
▪ a) easily soluble,
▪ b) have no or very low natural concentrations in stream,
▪ c) be conservative,
▪ d) easily detectable at low concentrations,
▪ e) ecofriendly,
▪ f) affordable

37. 37
Dilution gauging
▪ Advantage: suitable to any condition. Why?
▪ Disadvantage: difficult to find completely water soluble tracer. Sodium
Chloride (garam dapur) are commonly used
▪ Example of tracer:
▪ Chemical: Sodium cloride,sodium dicromat,manganese sulphate
▪ Dye: sodium fluoroscein, Rhodamine-WT
▪ Radioactive: Bromine-82,Sodium-24,Iodine-132
▪ 2 approach
▪ Sudden/Gulp injection
▪ Constant rate injection

39. 39
Dilution gauging: Constant Rate Injection
q
C
C
Q
q
Q
C
C
Q
q
Q
q
Q
q
q
C
C
.
.
2
1
1
2
1
2







C1,q
C2(q+Q)
Q
Unknown river flow, Q m3/s
•Tracer of known concentration C1(kg/m3) releases at point 1 at
constant rate, Q m3/s
•After sometimes, measure the water concentration at point
2, C2(kg/m3)

40. 40
Example calculation
▪ 20 g/L of tracer injected at upstream of the river at rate 0.01 L/s. Concentration of
tracers at downstream is 5 ppb. Estimate the discharge of the river at downstrean.
Assume the initial concentration of tracer is very low.
Solution:
q =0.01 L/s = 10-5 m3/s
C1 = 20 g/L = 20 000 g/m3
C2 = 5 ppb = 5 x 10-6 g/L = 5 x 10-3 g/m3
Q = C1/C2 x q = (20 000/5 x 10-3 )x 10-5
= 40 m3/s = 40 000 L/s

41. 41
Conversion factor
▪ 1 g/L = 10-3
▪ 1 mg/L = 10-6 = 1 ppm
▪ 1 μg/L = 10-9 =1 x 10-3 g/m3 = 1 ppb

42. 42
Dilution gauging: Sudden Injection


2
1
2
1
t
t
dt
C
Q
VC
Where:
V = volume of tracers (m3)
t1=time of tracer induced at upstream(point 1)
t2=time of tracer detected at point 2
C1,V1
C2, Q2
Q
Unknown river flow, Q m3/s
•Tracer of known concentration C1(kg/m3)
and known volumeV m3/s releases at
point 1 at one short
•After certain time, water concentration
at point 2 are measured, C2(kg/m3)

43. 43
Example Calculation:
▪ 100 liter NaCL at concentration 10 g/L induced at river upstream. Average NaCl
concentration after an hour at 800 m distance, at downstream are 0.02 mg/L.
Estimate the river discharge at downstream.
▪ Solution:
s
m
x
t
C
VC
Q
t
QC
VC
dt
C
Q
VC
t
t
/
89
.
13
3600
x
10
2
10
x
1
.
0 3
5
2
1
2
1
2
1
2
1










44. 44
- Measure speed of small particles in the flow
- Can also track and subtract bottom speed
Sonic methods

45. Some gages are designed to measure just high flows

46. 46
HYDRAULIC STRUCTURES
▪ Used for small watersheds – such as experimental watersheds –
where need accurate, continuous flow measurements.
▪ Two types:Weirs, Flumes

47. 47
Weirs
▪ A weir or also known as low-head dam, used to
prevent flooding, measure water flow, and hold
water.
▪ Obstruct flow and force it through a notch
▪ Stage-Q relationship established mathematically for
different types of notches

48. 48
Weirs
▪ Generally used in small streams
▪ Various types
▪ V-notch for accurate low flow
▪ Rectangular
▪ Handles higher flows
▪ Less accurate at low flows
▪ Trapezoidal -- an intermediate weir
▪ Concerns
▪ Sediment & debris are trapped
▪ Leakage

49. 49
Discharge over weir

50. 50
Trapezoidal Weir

51. 51
TrapezoidalWeir

52. 52
RectangularWeir

53. 53
90 degreeV-notchWeir

54. 54
V-notchWeir
2
5
2
tan
2
15
8
H
g
C
Q d


▪ For small river
▪ Q (m3/s) can be determine using equation:
▪
▪ Where:
▪ H = head loss
▪ Cd = discharge coefficient
▪ g gravity acceleration
▪ θ angle of the v-notch

55. 55
90ºV-notchWeir
Q = 2.36CdH5/2

56. 56
Flumes
• An artificial open channel built to contain flow within a
designed cross-section and length
• No impoundment
• Water height in flume measured with a stilling well

57. 57
Flumes
▪ Used to measure flow in:
▪ water and wastewater treatment plants
▪ irrigation channels
▪ agricultural runoff
▪ runoff plots – research applications
▪ small watersheds

58. 58
Large Crest Flumes

59. 59
Long-throated Flume

60. 60
Short-throated Flume

61. 61
Parshall Flume

62. 62
H Flume

63. 63
Slope Area Method
▪ Manning Equation
▪ Chezy Equation

64. 64
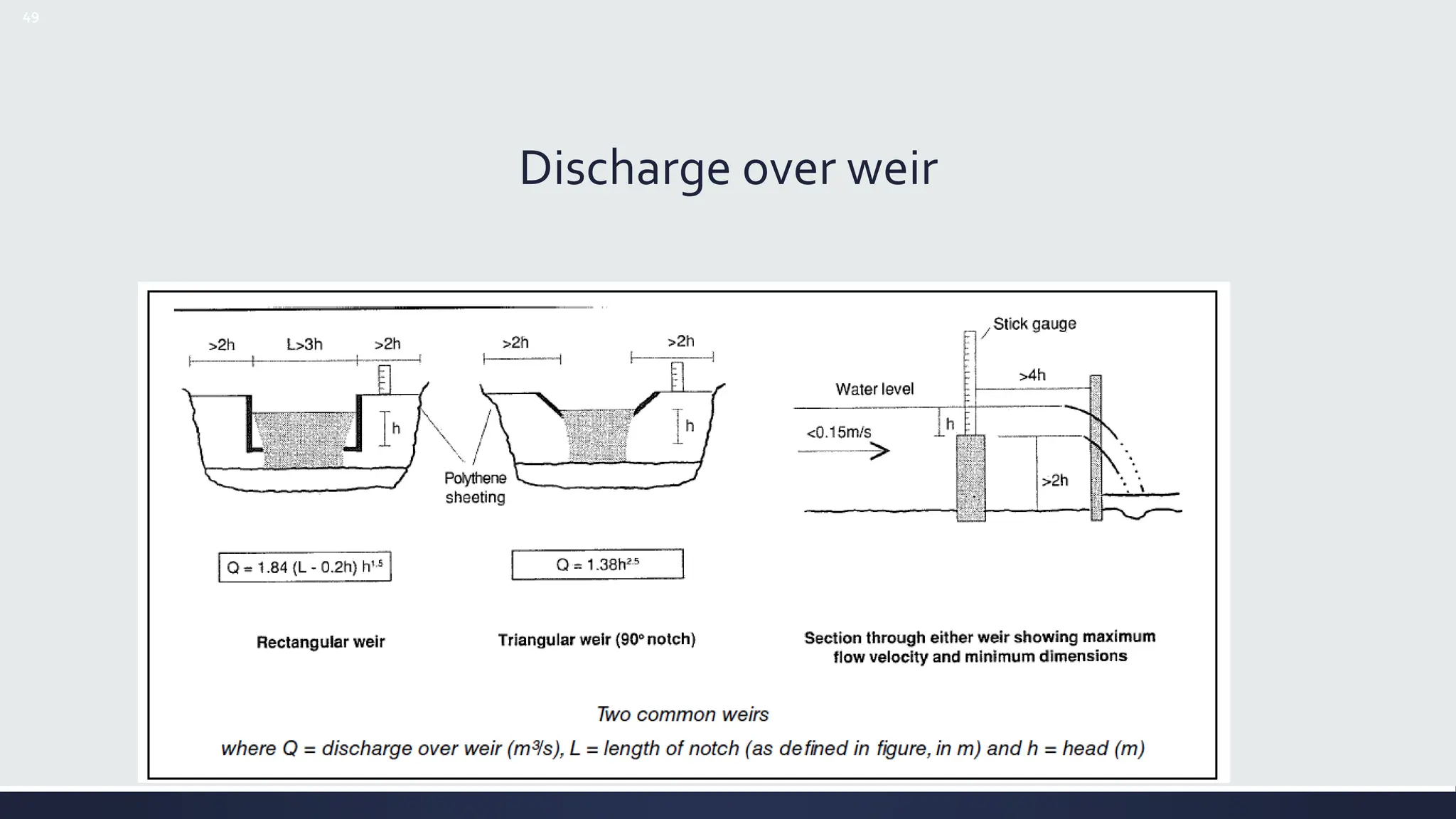
Estimating Discharge (Q) from channel features:
Manning’s Equation
2
1
3
2
1
S
R
n
v 
• v = average velocity (m/s)
• R = hydraulic radius
= [Area/wetted perimeter]
• S = Energy gradient, Approximated by water surface slope
• n = Manning’s roughness coefficient
Q = Av

65. 65
Q
K
1
D
A
Chezy Equation
▪ Based on Chezy formula,
▪ with A = flow cross-section area; C = Chezy Coefficient;
▪ R = hydraulic radius, A/P; and S = channel slope.
▪ For a given section, = constant whereas for a wide channel (W>10D) RD.
Therefore,
RS
AC
Q 
S
C
D
A
K
Q 

66. Thank You