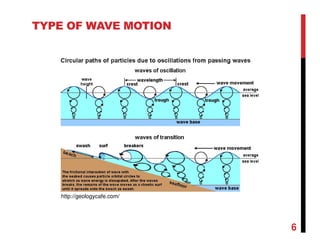
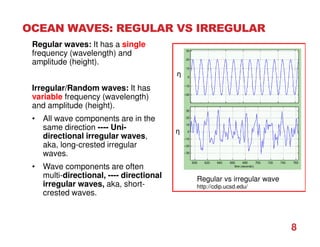
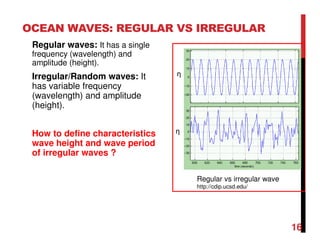
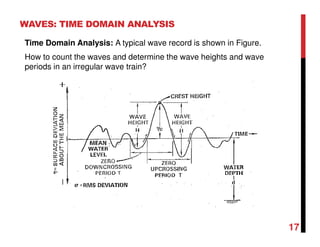
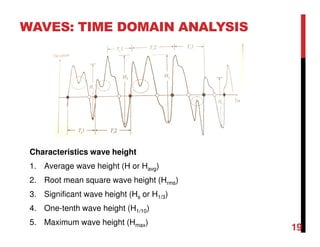
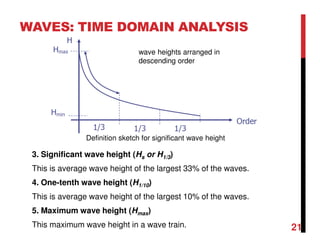
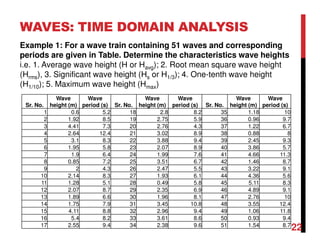
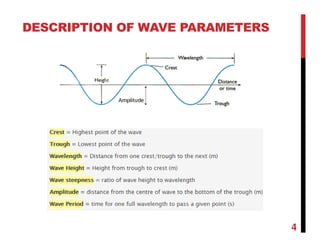
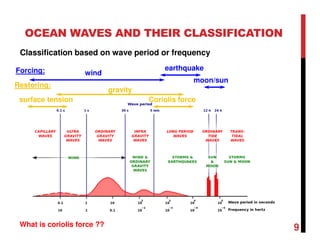
1. Waves are disturbances that transfer energy through a medium, such as water. They can be regular (single frequency/height) or irregular/random (variable frequency/height). 2. Important wave parameters include wavelength, period, frequency, speed, height, amplitude, and water elevation. 3. Ocean waves are classified based on their period/frequency and include capillary, gravity, and infragravity waves. 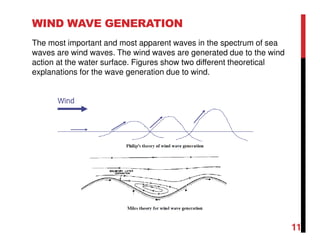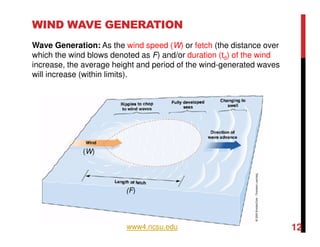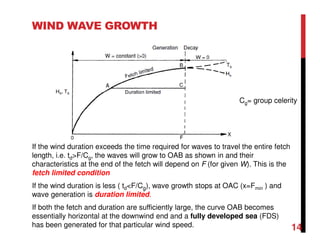4. Wind generates waves by transferring energy and momentum to water. Wave characteristics depend on wind speed, fetch (distance over which wind blows), and duration. Fully developed seas occur when energy input balances dissipation.

1. CHAPTER 2: WAVES AND TIDES
DR. MOHSIN SIDDIQUE
ASSISTANT PROFESSOR
1
0401444 - Coastal Eng.
University of Sharjah
Dept. of Civil and Env. Engg.

2. WAVE
A wave is an expression of the movement or progress of energy
through medium
A wave is a disturbance that propagates through space and time
usually with transfer of energy.
Ocean waves (irregular/random)Wave flume (regular)
Nortek USA 2

3. WAVE
Miniature wave tank
3https://www.youtube.com/watch?v=-m_VDE-BSgc

4. DESCRIPTION OF WAVE PARAMETERS
4

5. TYPE OF WAVE MOTION
Types of wave motion
5

6. TYPE OF WAVE MOTION
http://geologycafe.com/
6

7. DESCRIPTION OF WAVE PARAMETERS
7
L= wave length
T=wave period
f=frequency=2π/T
C=wave speed (celerity)
H=wave height
a= amplitude of wave (H/2)=horizontal
excursion of water particle
η=instantaneous surface water elevation
d= local water depth
Figure: Definition of progressive surface wave parameters
u and w =The horizontal and
vertical components of the
water particle velocity at any
instant.
ς and ε = The horizontal and
vertical coordinates of a water
particle at any instant.

8. OCEAN WAVES: REGULAR VS IRREGULAR
8
Regular waves: It has a single
frequency (wavelength) and
amplitude (height).
Irregular/Random waves: It has
variable frequency (wavelength)
and amplitude (height).
• All wave components are in the
same direction ---- Uni-
directional irregular waves,
aka, long-crested irregular
waves.
• Wave components are often
multi-directional, ---- directional
irregular waves, aka, short-
crested waves.
Regular vs irregular wave
http://cdip.ucsd.edu/
η
η

9. OCEAN WAVES AND THEIR CLASSIFICATION
Classification based on wave period or frequency
9
Forcing: earthquake
moon/sun
wind
Restoring:
gravity
surface tension Coriolis force
What is coriolis force ??

10. DESCRIPTION OF WAVE TYPES
Capillary waves: (wave length <1cm) are restored primarily by surface
tension.
Surface gravity waves: These exist at air-sea interface and are
restored by gravity
Infragravity waves are surface gravity waves with frequencies lower
than the wind waves
_________________________________________________________
Coriolis force is an inertial force that acts on objects that are in motion
relative to a rotating reference frame.
10

11. WIND WAVE GENERATION
The most important and most apparent waves in the spectrum of sea
waves are wind waves. The wind waves are generated due to the wind
action at the water surface. Figures show two different theoretical
explanations for the wave generation due to wind.
11

12. WIND WAVE GENERATION
Wave Generation: As the wind speed (W) or fetch (the distance over
which the wind blows denoted as F) and/or duration (td) of the wind
increase, the average height and period of the wind-generated waves
will increase (within limits).
12www4.ncsu.edu
(W)
(F)

13. WIND WAVE GENERATION
Wave Generation: For a given wind speed and unlimited fetch and
duration, there is a fixed limit to which the average height, period and
spectral energy will grow. At this limiting condition, the rate of energy
input from the wind to the waves is balanced by the rate of wave energy
dissipation due to wave breaking and turbulence. This condition is known
as fully developed sea.
13www4.ncsu.edu
(W)
(F)

14. WIND WAVE GROWTH
If the wind duration exceeds the time required for waves to travel the entire fetch
length, i.e. td>F/Cg, the waves will grow to OAB as shown in and their
characteristics at the end of the fetch will depend on F (for given W). This is the
fetch limited condition
If the wind duration is less ( td<F/Cg), wave growth stops at OAC (x=Fmin ) and
wave generation is duration limited.
If both the fetch and duration are sufficiently large, the curve OAB becomes
essentially horizontal at the downwind end and a fully developed sea (FDS)
has been generated for that particular wind speed. 14
Cg= group celerity

15. 15
WAVES STATISTICS AND PREDICTION
Short Term Analysis
Types of ocean waves: Irregular/random waves
Time domain analysis
Characteristic wave height and wave period
Rayleigh’s probability distribution
Frequency domain analysis
Concept of superposition of wave
Wave spectrum
Wave prediction
Long Term Analysis: Extreme wave analysis
Log-normal distribution
Gamma distribution
Weibull distribution
Gumbel distribution etc

16. OCEAN WAVES: REGULAR VS IRREGULAR
16
Regular waves: It has a single
frequency (wavelength) and
amplitude (height).
Irregular/Random waves: It
has variable frequency
(wavelength) and amplitude
(height).
How to define characteristics
wave height and wave period
of irregular waves ?
Regular vs irregular wave
http://cdip.ucsd.edu/
η
η

17. Time Domain Analysis: A typical wave record is shown in Figure.
How to count the waves and determine the wave heights and wave
periods in an irregular wave train?
WAVES: TIME DOMAIN ANALYSIS
17

18. Zero up-crossing and zero down-crossing method. It involves
counting the number of zero up-crossings or zero down-crossing in the
wave train and use this information to determine wave characteristics.
Zero up-crossing and zero down-crossing are the points of intersection
of water surface profile with the mean water level.
When the wave surface is traced from trough to crest, its intersection
point with mean water level is referred as zero up-crossing and from
crest to trough, it is known as zero down-crossing.
18
WAVES: TIME DOMAIN ANALYSIS

19. WAVES: TIME DOMAIN ANALYSIS
Characteristics wave height
1. Average wave height (H or Havg)
2. Root mean square wave height (Hrms)
3. Significant wave height (Hs or H1/3)
4. One-tenth wave height (H1/10)
5. Maximum wave height (Hmax)
19

20. WAVES: TIME DOMAIN ANALYSIS
1. Average wave height (H or Havg)
Where, N=number of waves; Hj= individual wave height
Similarly, average wave period corresponding to zero up-crossing and
zero-down crossing can be calculated as:
2. Root mean square height (Hrms)
∑
=
=
N
j
javg H
N
H
1
1
∑∑
==
==
N
j
jdownavgdown
N
j
jupavgup T
N
TANDT
N
T
1
,
1
,
1
,
1
,
∑
=
=
N
j
jrms H
N
H
1
21
20

21. WAVES: TIME DOMAIN ANALYSIS
3. Significant wave height (Hs or H1/3)
This is average wave height of the largest 33% of the waves.
4. One-tenth wave height (H1/10)
This is average wave height of the largest 10% of the waves.
5. Maximum wave height (Hmax)
This maximum wave height in a wave train.
wave heights arranged in
descending order
Definition sketch for significant wave height
21

22. WAVES: TIME DOMAIN ANALYSIS
Example 1: For a wave train containing 51 waves and corresponding
periods are given in Table. Determine the characteristics wave heights
i.e. 1. Average wave height (H or Havg); 2. Root mean square wave height
(Hrms), 3. Significant wave height (Hs or H1/3); 4. One-tenth wave height
(H1/10); 5. Maximum wave height (Hmax)
Sr. No.
Wave
height (m)
Wave
period (s) Sr. No.
Wave
height (m)
Wave
period (s) Sr. No.
Wave
height (m)
Wave
period (s)
1 0.6 5.2 18 2.8 8.2 35 1.18 10
2 1.92 8.5 19 2.75 5.9 36 0.96 9.7
3 4.41 7.3 20 2.76 4.3 37 1.22 6.7
4 2.64 12.4 21 3.02 8.9 38 0.88 8
5 3.1 8.3 22 3.88 9.4 39 2.45 9.3
6 1.95 5.8 23 2.07 8.9 40 3.86 5.7
7 1.9 6.4 24 1.99 7.6 41 4.66 11.3
8 0.85 7.2 25 3.51 6.7 42 1.46 8.7
9 2 4.3 26 2.47 5.5 43 3.22 9.1
10 2.14 8.3 27 1.93 6.1 44 4.36 5.6
11 1.28 5.1 28 0.49 5.8 45 5.11 8.3
12 2.07 8.7 29 2.35 6.9 46 4.89 9.1
13 1.89 6.6 30 1.96 8.1 47 2.76 10
14 1.75 7.9 31 3.45 10.8 48 3.55 12.4
15 4.11 8.8 32 2.96 9.4 49 1.06 11.8
16 5.4 8.2 33 3.61 8.6 50 0.93 9.4
17 2.55 9.4 34 2.38 9.6 51 1.54 8.7
22

23. WAVES: TIME DOMAIN ANALYSIS
Example: Solution:
Sr. No.
Wave height
(m)
Wave period
(s) H2
Wave height
in descending
order Hs or H1/3 H1/10
1 0.6 5.2 0.4 5.4 5.4 5.4
2 1.92 8.5 3.7 5.11 5.11 5.11
3 4.41 7.3 19.4 4.89 4.89 4.89
4 2.64 12.4 7.0 4.66 4.66 4.66
5 3.1 8.3 9.6 4.41 4.41 4.41
6 1.95 5.8 3.8 4.36 4.36
7 1.9 6.4 3.6 4.11 4.11
8 0.85 7.2 0.7 3.88 3.88
9 2 4.3 4.0 3.86 3.86
10 2.14 8.3 4.6 3.61 3.61
11 1.28 5.1 1.6 3.55 3.55
12 2.07 8.7 4.3 3.51 3.51
13 1.89 6.6 3.6 3.45 3.45
14 1.75 7.9 3.1 3.22 3.22
15 4.11 8.8 16.9 3.1 3.1
16 5.4 8.2 29.2 3.02 3.02
17 2.55 9.4 6.5 2.96 2.96
18 2.8 8.2 7.8 2.8 23

24. WAVES: TIME DOMAIN ANALYSIS
Sr. No.
Wave height
(m)
Wave period
(s) H2
Wave height
in descending
order Hs or H1/3 H1/10
19 2.75 5.9 7.6 2.76
20 2.76 4.3 7.6 2.76
21 3.02 8.9 9.1 2.75
22 3.88 9.4 15.1 2.64
23 2.07 8.9 4.3 2.55
24 1.99 7.6 4.0 2.47
25 3.51 6.7 12.3 2.45
26 2.47 5.5 6.1 2.38
27 1.93 6.1 3.7 2.35
28 0.49 5.8 0.2 2.14
29 2.35 6.9 5.5 2.07
30 1.96 8.1 3.8 2.07
31 3.45 10.8 11.9 2
32 2.96 9.4 8.8 1.99
33 3.61 8.6 13.0 1.96
34 2.38 9.6 5.7 1.95
35 1.18 10 1.4 1.93
24

25. WAVES: TIME DOMAIN ANALYSIS
Sr. No.
Wave height
(m)
Wave period
(s) H2
Wave height
in descending
order Hs or H1/3 H1/10
36 0.96 9.7 0.9 1.92
37 1.22 6.7 1.5 1.9
38 0.88 8 0.8 1.89
39 2.45 9.3 6.0 1.75
40 3.86 5.7 14.9 1.54
41 4.66 11.3 21.7 1.46
42 1.46 8.7 2.1 1.28
43 3.22 9.1 10.4 1.22
44 4.36 5.6 19.0 1.18
45 5.11 8.3 26.1 1.06
46 4.89 9.1 23.9 0.96
47 2.76 10 7.6 0.93
48 3.55 12.4 12.6 0.88
49 1.06 11.8 1.1 0.85
50 0.93 9.4 0.9 0.6
51 1.54 8.7 2.4 0.49
Havg=2.53 Tavg=8.10 Hrms=7.88 Hs=3.95 H1/10=4.89
Hmax=5.4
Note: A similar procedure can be applied to calculate characteristic wave period25

26. WAVES: TIME DOMAIN ANALYSIS
Example 2: Using the wave data given in table, calculate the
characteristic wave heights
26

27. WAVES: TIME DOMAIN ANALYSIS
Example 2: Solution
27
110/3=37
181/37 =4.90m

28. WAVES: TIME DOMAIN ANALYSIS
Wave Height Distribution:
In deep water the wave height
distribution of the individual waves
follows the Rayleigh-distribution.
Based on the Rayleigh-distribution
theoretical, the relationship between
wave parameters are:
Where N is number of individual waves in wave train
H100 represent average wave height (H100=Havg)
Hs=H1/3
Hs=1.416 Hrms
H100=0.886 Hrms
H100=0.63 Hs
Hmax/Hs=0.707 (lnN)0.5
Wave amplitude spectrum
28

29. WAVES: TIME DOMAIN ANALYSIS
Figure is useful when applying the Rayleigh distribution.
Line a gives the probability that any wave height will exceed the
height (H/Hrms) and line b gives the average height of the n highest
fraction of the waves.
29

30. WAVES: TIME DOMAIN ANALYSIS
Example: A wave record taken during a storm is analyzed by zero up-
crossing method it contains 205 waves. The average wave height is
1.72m. Estimate Hs, H1/5 and the number of wave in the record that
would exceed 2.5m height.
Given data:
N=205; Havg=H100=1.72m ; Hs=?; H1/20=H5=? (top 5%)
Number of waves with H>2.5m=?
Solution:
Root mean square Wave height:
H100=0.886 Hrms >> 1.72=0.886 Hrms >> Hrms=1.94m
Significant wave height:
Hs=1.416 Hrms >> Hs=1.416*(1.94) = 2.75m
30

31. WAVES: TIME DOMAIN ANALYSIS
For H1/20 corresponding to n=5% using Line b of figure we get;
H1/20/Hrms=1.98 >> H1/20=1.98(1.94)=3.84m
For given H=2.5m, corresponding to H/Hrms=2.5/1.94=1.29, we get P=0.19
using Line a of figure
Therefore, number of wave exceeding 2.5m height=205*0.19=38.95=39 waves
31

32. An irregular waves can be viewed as the superposition of a number of regular
waves of different frequencies (wave period) and amplitude (height).
WAVES: FREQUENCY DOMAIN ANALYSIS
In the case of wave record data, it is possible to decompose signature and derive
components through Fourier Transform. This process clearly indicates that any sea
state can be visualized as composition of infinite number of sine waves of different
amplitude and frequencies.
32

33. Wave Spectrum:
1. Wave energy spectrum: The energy for all directions at a particular
frequency S(f) is plotted as a function of only wave frequency.
2. Directional spectrum: A directional wave spectrum is produced when
the sum of the energy density in these component waves at each wave
frequency S(f, θ) is plotted versus wave frequency f and direction θ.
WAVES: FREQUENCY DOMAIN ANALYSIS
Wave energy is proportion to wave heights (amplitude)
S( f )
Wave train Wave energy spectrum
33

34. WAVES: FREQUENCY DOMAIN ANALYSIS
34

35. WAVES: SPECTRAL CHARACTERISTICS
1. Wave energy spectrum: An example of a wave energy density
spectrum is given in Figure below.
Characteristics and significant
wave parameters in frequency
domain are estimated from the
moments of the wave energy
density spectrum:
Characteristics parameters in
frequency domain are defined
as follows:
Where Hmo is spectral derived significant wave height i.e., Hmo=Hs=H1/3
35

36. WAVES: SPECTRAL CHARACTERISTICS
1. Wave energy spectrum:
o/avg m.H.HH 5072630 31100 ===
4
2
2
0
2,0
1
0
1,0 ;;
m
m
Tc
m
m
TzT
m
m
T mm ====
Where Tm0,1, Tm0,1 and Tc are wave period corresponding to mean frequency, zero-
up or down crossing and crest.
36

37. WAVES: SPECTRAL CHARACTERISTICS
As the Rayleigh distribution is a useful model for the expected
distribution of wave heights from a particular storm, it is also useful to
have a model of the expected wave spectrum generated by a
storm. Several one-dimensional wave spectra models have been
proposed.
Four commonly use spectrum in coastal engineering practice.
I. Bretschneider Spectrum
II. Pierson-Moskowitz Spectrum
III. JONSWAP Spectrum
IV. Shallow water TMA spectrum
37

38. WAVES: SPECTRAL CHARACTERISTICS
II. Pierson-Moskowitz Spectrum (PM spectrum)
Pierson and Moskowitz (1964) gave an expression for spectral density function
E(f) to describe waves in a field corresponding to fully developed sea for wind
speed varying 20-40 knots*.
An other expression for E(f) incorporating peak frequency is given by:
*1knot=0.514444m/s 38

39. WAVES: SPECTRAL CHARACTERISTICS
Wave spectrum given in table is obtained
based on Pierson-Moskowitz expression for
spectral density corresponding to wind speed of
20m/s.
Determine spectral characteristics.
Frequency
(f)
Spectral
density, E(f)
0.03 0
0.04 0.107
0.05 19.737
0.06 77.201
0.07 94.739
0.08 78.015
0.09 55.698
0.1 37.982
0.11 25.73
0.12 17.597
0.13 12.229
0.14 8.653
0.15 6.235
0.16 4.572
0.17 3.407
0.18 2.577
0.19 1.977
0.2 1.536
39

40. WAVES: SPECTRAL CHARACTERISTICS
f E(f)
Simpson
multiplier
(sm)
E(f).(sm) E(f).f.(sm) E(f).f2
.(sm) E(f).f4
.(sm)
A B C D=B.C E=A.B.C F=(A^2).B.C G=(A^4).B.C
0.03 0 1 0 0 0 0
0.04 0.107 4 0.428 0.017 0.001 0.000
0.05 19.737 2 39.474 1.974 0.099 0.000
0.06 77.201 4 308.804 18.528 1.112 0.004
0.07 94.739 2 189.478 13.263 0.928 0.005
0.08 78.015 4 312.06 24.965 1.997 0.013
0.09 55.698 2 111.396 10.026 0.902 0.007
0.1 37.982 4 151.928 15.193 1.519 0.015
0.11 25.73 2 51.46 5.661 0.623 0.008
0.12 17.597 4 70.388 8.447 1.014 0.015
0.13 12.229 2 24.458 3.180 0.413 0.007
0.14 8.653 4 34.612 4.846 0.678 0.013
0.15 6.235 2 12.47 1.871 0.281 0.006
0.16 4.572 4 18.288 2.926 0.468 0.012
0.17 3.407 2 6.814 1.158 0.197 0.006
0.18 2.577 4 10.308 1.855 0.334 0.011
0.19 1.977 2 3.954 0.751 0.143 0.005
0.2 1.536 1 1.536 0.307 0.061 0.002
Sums 1347.9 114.967 10.770 0.129
=Sum0 =Sum1 =Sum2 =Sum4 40

41. WAVES: SPECTRAL CHARACTERISTICS
∆f 0.01
m0=(1/3)*(∆f)*Sum0 4.493
m1=(1/3)*(∆f)*Sum1 0.383
m2=(1/3)*(∆f)*Sum2 0.036
m4=(1/3)*(∆f)*Sum4 0.000
Havg=2.507(m0)0.5 5.314 m
Hs=4.004(m0)0.5 8.487 m
H1/10=5.09(m0)0.5 10.789 m
H1/100=6.673(m0)0.5 14.144 m
Tm0,1=m0/m1 11.724 S
Tm0,2=Tz=(m0/m2)0.5 11.187 S
Tc=(m2/m4)0.5 9.140 S
Determine spectral moments using following formula
mi=(1/3)*(∆f)*Sumi
41

42. WAVES: FREQUENCY DOMAIN ANALYSIS
2. Directional spectrum
Characteristics of waves in deep waters (H, T and direction) are
dependent on wind speed, its direction, duration and fetch.
Thus, at any given time, an observer in sea is bound to experience
assorted waves approaching from different direction.
42
www.mhl.nsw.gov.au

43. The most widely used method for wave height and wave period
prediction from the wind data is probably the one described in the
Coastal Engineering Manual by US army corps of Engineers. This
method utilizes JONSWAP wave spectrum.
According to this procedure, the wind speed has to be specified on the
sea at 10m above the water level. The measured wind speed at any
other level should be adjusted using one-seventh-root law given as:
WAVE PREDICTION
1
43

44. 44
WAVE PREDICTION
(2)
(3)
(4)
(5)
(6)
(7)

45. 45
WAVE PREDICTION
(8)
Eq. (8)
Eq. (2)& (3)
(9)

46. 46
WAVE PREDICTION

47. 47
WAVE PREDICTION

48. THANK YOU
48

49. 49
TIDES
Astronomical tide (tide) is a periodic rising and falling of sea level
caused by the gravitational attraction of the Moon, Sun and other
astronomical bodies acting on the rotating earth.
Tides follow the moon closely than they do the sun.
Primary forces:
The primary tide generation forces are:
• 1. Gravitational attraction by the moon
• 2. Gravitational attraction by the sun
• 3. Centrifugal forces (equal and opposite to the above)
• Tides are longer period waves as compared to wind generated waves
• Primary periods of tides are 12.4 hours and 24 hours.
• Because of its long period, tide propagates as a shallow water wave even
over the deepest parts of the ocean

50. 50
TIDES
As the tide propagates onto the continental shelf and into bays and
estuaries, it is affected by:
• 1. Near-shore hydrography
• 2. Friction
• 3. Coriolis acceleration
• 4. Resonance effects
How the above factors affect the tides is described below:
• 1. Convergence of shoreline causes the increase in tidal amplitude,
divergence of shorelines cause the decrease in it. Decreasing
water depths near the shoreline cause shoaling.
• 2. Friction causes the amplitude to decrease.
• 3. The Coriolis acceleration causes the water flow to the right in
northern hemisphere and to the left in southern hemisphere.
• 4. Due to very low steepness, tide has relatively high reflectivity.

51. 51
TIDES: EARTH AND MOON

52. TIDES: EARTH AND MOON
Tide level due to earth rotation
https://oceanservice.noaa.gov/education/tutorial_
tides/tides05_lunarday.html
Movement of tidal bulge
https://oceanservice.noaa.gov/education/tutori
al_tides/media/supp_tide04.html
52

53. 53
TIDES: EARTH, MOON AND SUN
https://oceanservice.noaa.gov/facts/springtide.html

54. TIDES: SPRING AND NEAP
Spring tide: During full or new moons—which occur when the Earth,
sun, and moon are nearly in alignment—average tidal ranges are slightly
larger. This occurs twice each month. The moon appears new (dark)
when it is directly between the Earth and the sun. The moon appears full
when the Earth is between the moon and the sun. In both cases, the
gravitational pull of the sun is "added" to the gravitational pull of the
moon on Earth, causing the oceans to bulge a bit more than usual. This
means that high tides are a little higher and low tides are a little lower
than average.
Neap tides: Seven days after a spring tide, the sun and moon are at
right angles to each other. When this happens, the bulge of the ocean
caused by the sun partially cancels out the bulge of the ocean caused by
the moon. This produces moderate tides known as neap tides, meaning
that high tides are a little lower and low tides are a little higher than
average. Neap tides occur during the first and third quarter moon, when
the moon appears "half full."
54

55. TIDES: SPRING AND NEAP
Dominic Reeve et al. (2005)
Coastal Eng: processes, theory
and design practice
55

56. TIDAL COMPONENTS (TIDAL CONSTITUENTS)
56https://tidesandcurrents.noaa.gov/publications/Tidal_Analysis_and_Predictions.pdf

57. TIDAL COMPONENTS:
There are over 390 active tidal components having periods ranging from 8 hours
to 18.6 years. These are extracted from measured data. Time period of each
component is determined from astronomical analysis. The phase angle and
amplitude depend on local conditions and therefore generally determined
empirically.
57Tidal components are helpful for tide prediction

58. TIDAL RATIO
predominantly semi-diurnal
58
https://oceanservice.noaa.gov/
Note: For a mixed tide: Nf <1.5 it is predominantly
semi-diurnal and; if Nf >1.5, it is predominantly diurnal
1.5

59. TYPES OF TIDAL CYCLES
The tidal record at any location can generally be classified as one
of three types:
Diurnal: An area has a diurnal tidal cycle if it experiences one high and
one low tide every lunar day
Semidiurnal: An area has a semidiurnal tidal cycle if it experiences two
high and two low tides of approximately equal size every lunar day
Mixed: An area has a semidiurnal tidal cycle if it experiences two high
and two low tides of different size every lunar day
59Make some corrections on this slide.

60. TYPES OF TIDAL CYCLES
Example: The tidal constituents for four harbors are given in the
following table. Classify the tidal regime in each harbor using the
tidal ratio.
Solution:
60

61. TIDE LEVELS AND DATUM
61

62. TIDE LEVELS AND DATUM
Note: All tide level are averaged over a period of 19 years.
MEAN SEA LEVEL (MSL). The average height of the surface of the sea for all stages of the
tide over a 19-year period, usually determined from hourly height readings. Not necessarily
equal to MEAN TIDE LEVEL.
TIDAL RANGE. The difference of elevation between high and low waters is termed as tidal
range. It is equal to MHW minus MLW.
MEAN HIGH WATER (MHW). The average height of the high waters over a 19-year period.
MEAN LOW WATER (MLW). The average height of the low waters over a 19-year period.
62

63. TIDE PREDICTION
Harmonic analysis describes the variation in water level as the sum of a
constant mean level, and contributions from specific harmonics (tidal
components);
Where, η is the water level, Z0 is the mean water level above (or below)
local datum, i is the angular frequency** of ith harmonic (obtained from
astronomical theory), ai is the amplitude of the ith harmonic (obtained from
astronomical theory), ϕi is the phase of ith harmonic, n is the number of
harmonics used to generate the tide, t is the time
63
∑=
−Ω+=
n
i
iio itaZ
1
)cos( φη
**Frequency, f=1/T (e.g., cycle/hr)
Angular frequency, (or ω) =2π/T (e.g., radian/hr)

64. TIDE PREDICTION
64

65. TIDE PREDICTION
Example: Frequency, amplitude & phase angle of the main tidal
constituents are given in table below:
Plot each tidal component (for 3 months)
Plot predicted tide levels (for 3 months)
Solution:
Where, t ranges from 0 to 3*30*24 hrs
(tidal constituents)
65
∑=
−Ω+=
n
i
iio itaZ
1
)cos( φη
)cos(...)cos()cos( 111222222 KKKNNNMMMo tatataZ φφφη −Ω++−Ω+−Ω+=

66. Tidal Parameters Zo M2 N2 S2 K2 O1 K1
Amplitude (m) 2.78 1.56 0.3 0.52 0.14 0.16 0.15
Frequency (1/T) 0 0.081 0.079 0.083 0.084 0.039 0.042
Frequency (2π/T) 0 0.508 0.496 0.521 0.527 0.245 0.264
Phase Shift 0 160 136 206 204 116 285
T (hrs) Zo η1 η2 η3 η4 η5 η6 η**
0 2.78 -1.466 -0.216 -0.467 -0.128 -0.070 0.039 0.472
1 2.78 -1.020 -0.091 -0.519 -0.139 -0.033 0.000 0.977
2 2.78 -0.317 0.056 -0.432 -0.113 0.006 -0.039 1.941
3 2.78 0.467 0.190 -0.231 -0.055 0.044 -0.076 3.119
4 2.78 1.133 0.278 0.031 0.017 0.080 -0.107 4.212
5 2.78 1.512 0.298 0.286 0.084 0.111 -0.131 4.941
6 2.78 1.508 0.247 0.464 0.129 0.136 -0.145 5.119
7 2.78 1.122 0.136 0.519 0.139 0.152 -0.150 4.699
8 2.78 0.452 -0.007 0.437 0.111 0.160 -0.144 3.787
9 2.78 -0.333 -0.149 0.238 0.052 0.157 -0.129 2.617
10 2.78 -1.033 -0.255 -0.024 -0.020 0.146 -0.104 1.490
11 2.78 -1.471 -0.299 -0.279 -0.087 0.125 -0.072 0.696
12 2.78 -1.538 -0.272 -0.461 -0.130 0.098 -0.035 0.442
13 2.78 -1.214 -0.178 -0.520 -0.138 0.064 0.004 0.797
14 2.78 -0.584 -0.042 -0.440 -0.109 0.027 0.043 1.675
15 2.78 0.195 0.104 -0.244 -0.049 -0.013 0.079 2.852
16 2.78 0.924 0.226 0.017 0.023 -0.051 0.109 4.028
17 2.78 1.419 0.293 0.273 0.090 -0.086 0.132 4.901
18 2.78 1.555 0.289 0.457 0.132 -0.116 0.146 5.243
19 2.78 1.297 0.215 0.520 0.138 -0.139 0.150 4.961
20 2.78 0.711 0.090 0.444 0.106 -0.154 0.143 4.120
21 2.78 -0.056 -0.057 0.251 0.046 -0.160 0.127 2.931
22 2.78 -0.808 -0.190 -0.009 -0.027 -0.156 0.101 1.691
23 2.78 -1.356 -0.278 -0.267 -0.092 -0.143 0.069 0.714
24 2.78 -1.560 -0.298 -0.454 -0.133 -0.121 0.032 0.246
**η= Zo+η1+ η2 + η3 + η4 + η5 + η6

67. -2
-1
0
1
2
3
4
5
6
0 20 40 60 80 100 120 140 160 180
waterlevel(m)
time (hrs)
Zo
η1
η2
η3
η4
η5
η6
η

68. 68
THANK YOU

69. 69
TSUNAMI
The term tsunami comes from the Japanese language meaning
harbour ("tsu"), and wave ("nami"). i.e., harbor wave
Tsunamis are gravity waves generated by underwater disturbances.
These include landslides, volcanic eruptions, earthquakes as well as
nuclear explosions.
They are characterized by periods of between 5 min to 1 h, with a
common range of periods being around 20–30 min. Tsunamis are often
generated in the deep ocean, where water depths may be more than
1000m, and have a small wave height.
They may propagate vast distances without suffering significant
dissipation. Incoming tsunamis can amplify dramatically due to shoaling
and refraction as they approach the shoreline.

70. TSUNAMI
70

71. 71
TSUNAMI: CHARACTERISTICS
• Extremely long wave lengths (100-200km)
• Long period (20-30min)
• Can travel at speed over 700Km/hr
• Low wave height (1-2m) in the open ocean, so pass beneath ships
unnoticed
• Affect entire water column, so carry more energy than surface
waves
• Act as a shallow-water wave** even in deep oceanic water
• Build up to extreme heights in shallow coastal areas
**Depth of water < (1/20) wave length

72. 72
TSUNAMI: SPEED & TRAVEL TIME
Speed of travel of tsunami wave, c, can be calculated using following
equation:
Travel time, tT, from the source of a tsunami to another site can be
estimated by adding the travel time along successive intervals along
the wave orthogonal that connects two points as follows:
Where d is average water depth over the interval having a length, ∆S
and g is acceleration due to gravity.
gdc =
∑
∆
=
gd
S
tT

73. TSUNAMI: EXAMPLE
Example: An earthquake off the coast of Japan causes a tsunami
wave. Estimate how long will it take for the wave to reach the West
Coast of North America. (The pacific coast may be assumed to be
4000km wide and 6km deep).
Solution: Using shallow water approximation, speed of tsunami may
be approximated as:
The time of travel can be calculated as:
smgdc /2426000*81.9 ===
hourss
c
S
gd
S
tT 6.416500
242
000,000,4
====
∆
= ∑
73

74. TSUNAMI: EXAMPLE
Example: A wave in a tsunami has a period of 30min and wave height,
Ho, of 0.5m at a point where the ocean has a depth of 4km.
(a). Calculate phase speed, co, and wave length, Lo, of this wave.
(b). Calculate its phase speed, ci, wave length, Li, and height, Hi, in a
coastal water depth of 15m accounting shoaling effects only.
Solution:
(a).
d/Lo=4000/356400=0.01 < 1/20; therefore, wave is shallow water wave
74

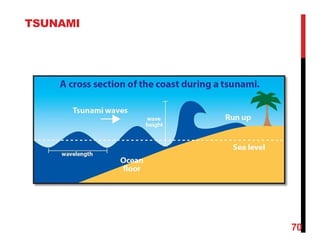
75. TSUNAMI: EXAMPLE
Solution:
(b). To determine the nearshore characteristics, we assume there is
negligible energy dissipation and wave energy in deep and near-shore
are same.
Energy of wave=E=[ρgH2L]/16
L=T (c)
Power of wave=E/T
Eo= Ei
75

76. 76
THANK YOU