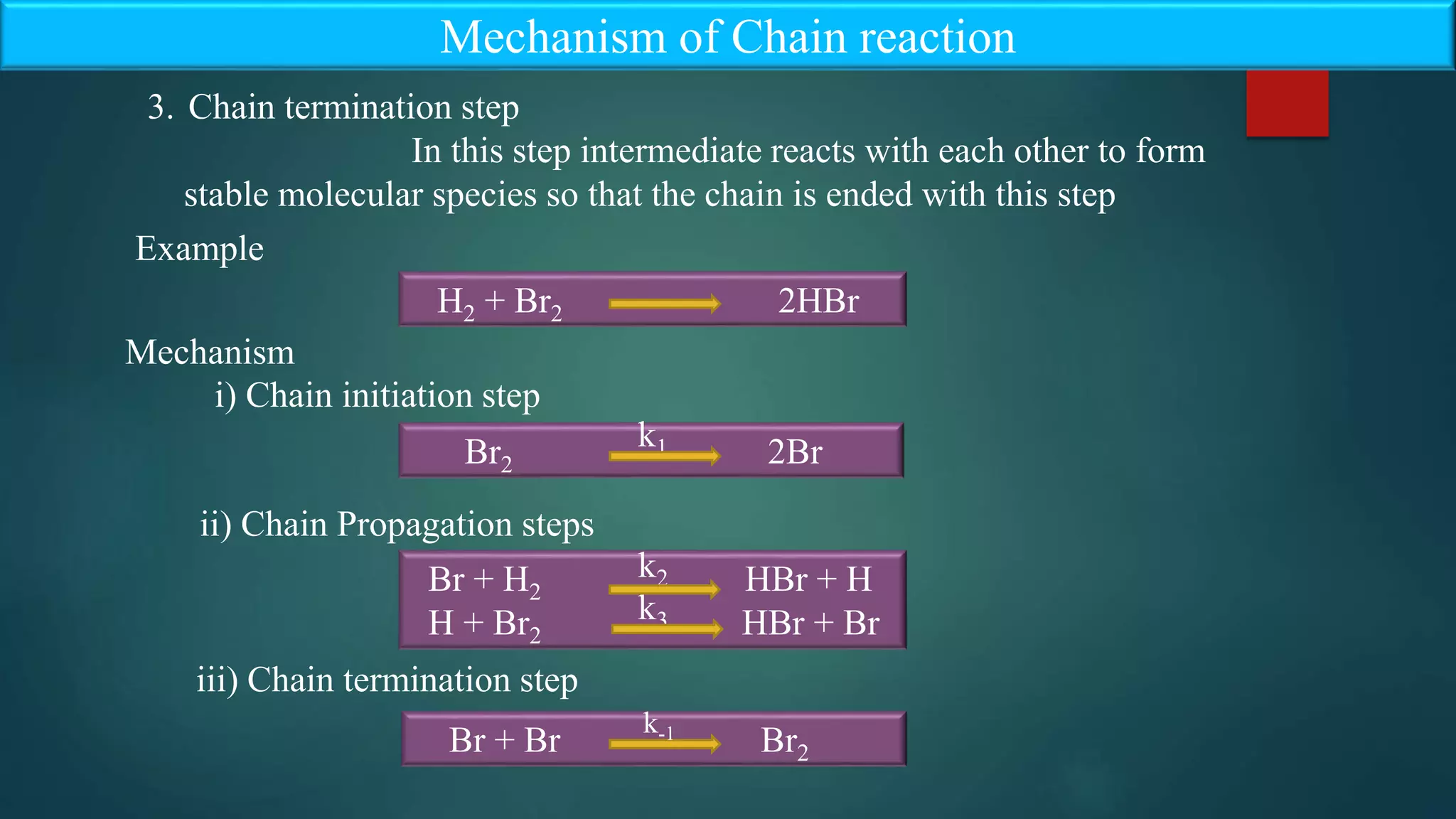
The document discusses the kinetics of chain reactions, highlighting their three main steps: initiation, propagation, and termination, with examples provided such as the reaction between hydrogen and bromine. It also outlines characteristics of chain reactions, like the probability factor often being greater than unity and the influence of external factors on reaction speed. The steady state approximation is explored in detail, demonstrating its application in the kinetics of thermal decomposition of acetaldehyde.

1. KINETICS OF CHAIN REACTIONS
Dr.P.GOVINDARAJ
Associate Professor & Head , Department of Chemistry
SAIVA BHANU KSHATRIYA COLLEGE
ARUPPUKOTTAI - 626101
Virudhunagar District, Tamil Nadu, India

2. KINETICS OF CHAIN REACTIONS
Chain reactions
Chemical reactions in which highly reactive short-lived species like atoms (or)
free radicals are produced as intermediates which carry out the reaction at a
rapid rate for a long time are called Chain reactions.
Mechanism of Chain reaction
Chain reaction occur mainly by the following three steps
1. Chain initiation step
In this step active intermediates are produced
2. Chain propagation steps
In these steps active intermediates reacts with reactant
gives product and another active intermediate and this is repeated as a chain
until the reactants (or) active intermediate disappear.

3. Example
H2 + Br2 2HBr
Mechanism
i) Chain initiation step
Br2 2Br
ii) Chain Propagation steps
Br + H2 HBr + H
H + Br2 HBr + Br
k1
k2
k3
iii) Chain termination step
Br + Br Br2
3. Chain termination step
In this step intermediate reacts with each other to form
stable molecular species so that the chain is ended with this step
k-1
Mechanism of Chain reaction

4. Characteristics of chain reactions
i) The probability factor P of chain reactions is generally greater than unity
ii) The chain reactions, sometimes possess excessive speeds which may lead to explosion
iii) The chain reactions begin at zero rate and then rises to maximum and then falls of
with time shown in the diagram
iv) As the chain reaction begin at zero rate , it therefore requires enough time so that the rate
of the reaction could be detected experimentally
v) The speed of the chain reactions is retarded or accelerated by traces of other substances

5. vi) The rate of chain reactions is influenced by the changes in shape of the containing vessel.
vii)The chain reactions are rarely of simple orders but have integral orders which depends
upon the vessel shape and other experimental conditions.
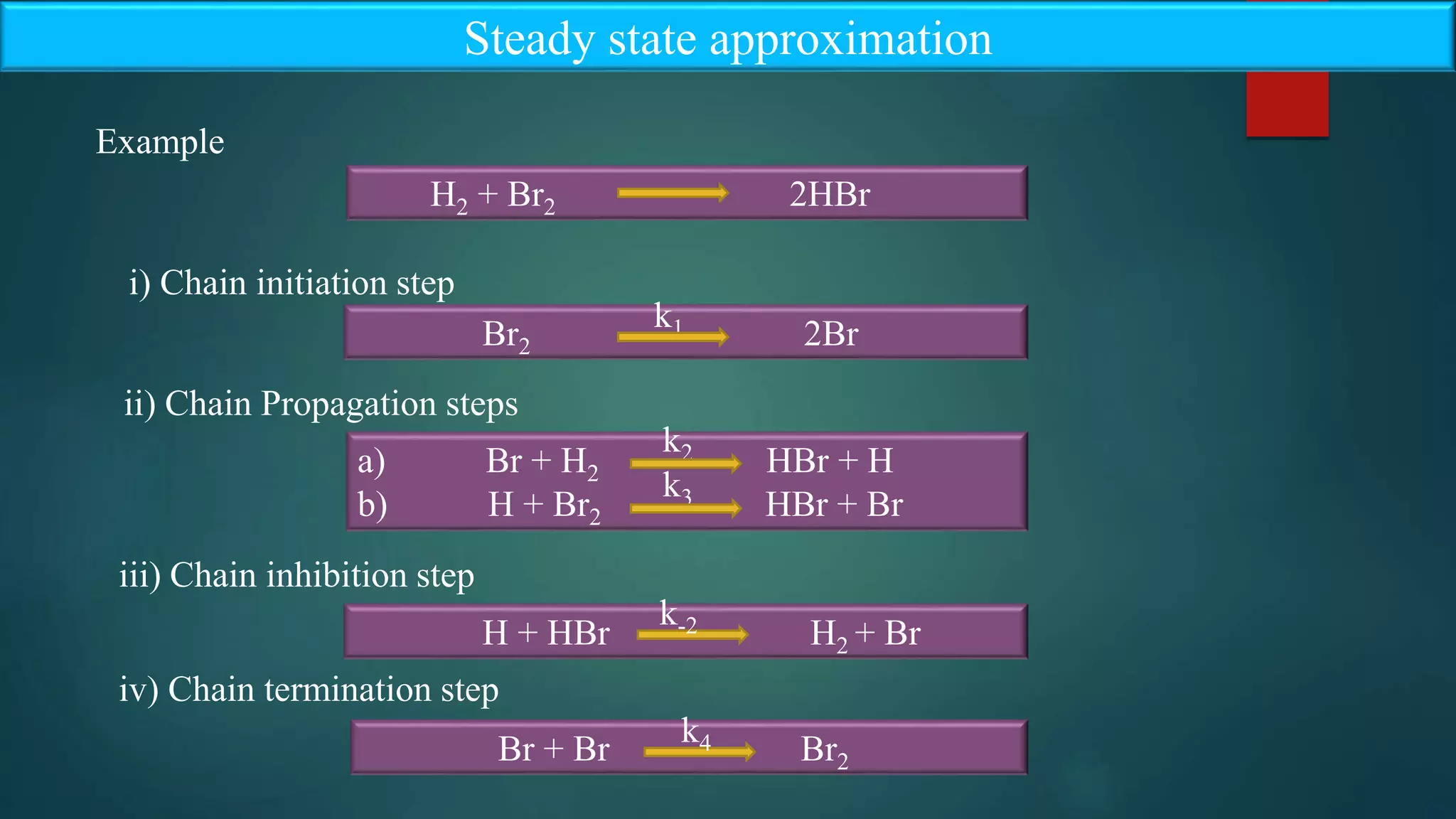
Steady state approximation states that the rate of formation of active intermediate is equal
to the rate of disappearance of active intermediate in the chain reactions
Steady state approximation
i.e., the rate of formation of intermediate (R) and the rate of disappearance of intermediate
(R) must be equal to zero
𝑑[𝑅]
𝑑𝑡
= −
𝑑[𝑅]
𝑑𝑡
= 0
Characteristics of chain reactions

6. Example
H2 + Br2 2HBr
i) Chain initiation step
Br2 2Br
ii) Chain Propagation steps
a) Br + H2 HBr + H
b) H + Br2 HBr + Br
k1
k2
k3
iii) Chain inhibition step
H + HBr H2 + Br
k-2
iv) Chain termination step
Br + Br Br2
k4
Steady state approximation

7. On applying steady state approximation to the intermediate H
𝑑[𝐻]
𝑑𝑡
= Rate of formation of [H] – Rate of disappearance of [H] = 0 ------(1)
Rate of formation of [H] = k2[Br][H2] ------(2)
Rate of disappearance of [H] = k3[H][Br2] + k-2[H][HBr] ------(3)
Substitute (2) and (3) in (1) we get
𝑑[𝐻]
𝑑𝑡
= k2[Br][H2] - k3[H][Br2] - k-2[H][HBr] = 0
Steady state approximation

8. Kinetics of thermal decomposition of Acetaldehyde
CH3CHO CH4 + CO
Mechanism
i) Chain initiation step
CH3CHO CH3 + CHO
ii) Chain Propagation steps
CH3 + CH3CHO CH4 + CH3CO
CH3CO CH3 + CO
k1
k2
k3
iii) Chain termination step
CH3 + CH3 C2H6
k4
The radical CHO undergoes further reactions, but for simplicity they are ignored here
The Thermal decomposition of Acetaldehyde is

9. i.e., Rate of formation of methyl radical = Rate of disappearance of methyl radical
𝑑[𝐶𝐻4
]
𝑑𝑡
= k2[CH3][CH3CHO] ------(1)
Applying steady state approximation on methyl radicals
The rate of formation of Methane is
k1[CH3CHO] + k3[CH3CO] = k2[CH3][CH3CHO] + k4[CH3][CH3]
k1[CH3CHO] + k3[CH3CO] - k2[CH3][CH3CHO] - k4[CH3][CH3] = 0 ------(2)
Kinetics of thermal decomposition of Acetaldehyde

10. Applying steady state approximation on CH3CO radicals
i.e., Rate of formation of CH3CO = Rate of disappearance of CH3CO
k2[CH3][CH3CHO] = k3[CH3CO]
k2[CH3][CH3CHO] - k3[CH3CO]= 0 ------(3)
Adding equation (2) and (3) we get the concentration of methyl radicals
k1[CH3CHO] + k3[CH3CO] - k2[CH3][CH3CHO] - k4[CH3][CH3] + k2[CH3][CH3CHO] -
k3[CH3CO] = 0
k1[CH3CHO] - k4[CH3]2 = 0
k1[CH3CHO] = k4[CH3]2
Kinetics of thermal decomposition of Acetaldehyde

11. k1[CH3CHO] = k4[CH3]2
[CH3]2 =
k1
k4
[CH3CHO]
k4[CH3]2 = k1[CH3CHO]
[CH3] = (
k1
k4
)1/2[CH3CHO]1/2
-------(4)
Substitute (4) in (1) we get
𝑑[𝐶𝐻4]
𝑑𝑡
= k2(
k1
k4
)1/2[CH3CHO]1/2 [CH3CHO]
𝑑[𝐶𝐻4]
𝑑𝑡
= k2(
k1
k4
)1/2[CH3CHO]3/2
This is the rate equation for thermal decomposition of CH3CHO and the
overall order of this reaction is 3/2
Kinetics of thermal decomposition of Acetaldehyde