Molecular orbital theory (MOT) is an alternative model to valence bond theory that explains how atomic orbitals from different atoms combine to form molecular orbitals. The linear combination of atomic orbitals (LCAO) method considers the probability of finding electrons in atomic orbitals from different atoms. According to the LCAO method, molecular orbitals are formed from constructive and destructive interference of atomic orbitals. MOT can be used to explain bonding in homonuclear diatomic molecules like N2 and O2, heteronuclear diatomic molecules like CO and NO, and polyatomic molecules like CO2 and SF6. It can also describe bonding in octahedral transition metal complexes like hexaaquoferrate(II) ion

1. MOLECULAR
ORBITAL
THEORY
Pallavi Kumbhar
MSc. Part I

2. Contents
01 Introduction
02 LCAO Method
03 Combination of Orbitals
04 Rules of LCAO
05 Examples of MOT
06 Summary
07 Refrences

3. 01
Introduction
First proposed by F. Hund and R.S. Mulliken in 1932.
 It is an alternative model for valence bond theory and explains most of the theories which
VBT could not.
 In MOT, the valency electrons are considered as particles or waves. Thus atomic orbitals
from different atoms are combined to produce molecular orbitals.
 The wave function describing a molecular orbital are obtained by one of the two procedures.
1. Linear Combination of Atomic Orbitals (LCAO)
2. United atom method.

4. 02
LCAO Method
• Consider two atoms A and B which have atomic orbitals described by the wave functions Ψ(A) and
Ψ(B)
Ψ(AB) = N(c1Ψ(A) + c2Ψ(B))
• The probability of finding an electron in a volume of space dv is Ψ2 dv, so the probability density
for the combination of two atoms is,
Ψ2
(AB) = (c12 Ψ2
(A) + 2c1c2 Ψ(A) Ψ(B) + c2
2 Ψ2
(B))
• Two combinations of the wave functions Ψ(A) and Ψ(B) are possible:
1. Ψ(g) = N{Ψ(A) + Ψ(B)}
2. Ψ(u) = N{Ψ(A) + (-Ψ(B))} = N{Ψ(A) - Ψ(B)}

5. 03
Combination of Orbitals

6. 04
Rules of Linear Combination of Atomic Orbitals
Rules to decide which atomic orbitals maybe combined to form molecular orbitals.
1.The atomic orbitals must be roughly of the same energy.
2.The orbitals must overlap one another as much as possible.
3.In order to produce bonding and antibonding MOs, either the symmetry of the two atomic orbitals must
remain unchanged when rotated about the internuclear line, or both atomic orbitals must change symmetry in
an identical manner.
Each atomic and molecular orbital has a definite energy and is defined by four quantum numbers.
1. The principle quantum number; n.
2. The azimuthal quantum number; l.
3. The magnetic quantum number; m.
4. The spin quantum number; s.

7. 05
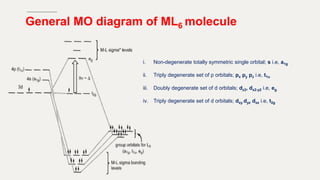
Examples of MOT
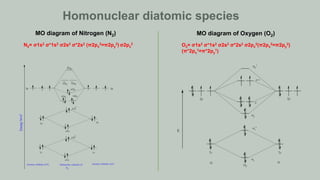
Homonulear diatomic species
Heteronuclear diatomic species
Polyatomic species.
a. CO2
b. SF6
Octahedral complexes of 1st transition series.
a. Hexaaquo ferrate (II) ion: [Fe(H2O)6]2+

8. Homonuclear diatomic species
N2= σ1s2 σ*1s2 σ2s2 σ*2s2 (π2px
2=π2py
2) σ2pz
2 O2= σ1s2 σ*1s2 σ2s2 σ*2s2 σ2pz
2(π2px
2=π2py
2)
(π*2px
1=π*2py
1)
MO diagram of Nitrogen (N2) MO diagram of Oxygen (O2)

9. Heteronuclear diatomic species
NO=σ1s2 σ*1s2 σ2s2 σ*2s2 σ2pz
2(π2px
2=π2py
2) π*2px
1
MO diagram of Carbon Monoxide (CO)
CO=σ1s2 σ*1s2 σ2s2 σ*2s2 (π2px
2=π2py
2) σ2pz
2
MO diagram of Nitric Oxide (NO)

10. MO diagram of Carbondioxide (CO2)
• CO2 is triatomic linear molecule like
BeH2.
• C(6)= 1s2 2s2 2p2
O(8)= 1s2 2s2 2p4
• The 2s orbitals of Oxygen atom are not
involved in bonding.
• First the two Oxygen atoms overlap to
form group orbitals and these then
overlap with Carbon atom.
Polyatomic species

11. • SF6 is a hypervalent molecule.
• Hypervalent molecule is one that contains a
Group 15–18 central atom having a formal
oxidation number higher than its lowest
oxidation state.
• s orbital; i.e, a1g
p orbitals; px py pz i.e, t1u
d orbitals; dz2, dx2-y2 i.e, eg
MO diagram of SF6 molecule

12. In an octahedral complex (ML6), on the basis of MOT, the formations of six M-L σ bonds can
be explained in detail on the basis of the following three steps.
I. Identification of central metal and ligand orbitals that are suitable for bonding on the
basis of symmetry requirements.
II. Construction of ligand group orbitals from ligand atomic orbitals.
III. Development of σ MO diagram for complex ML6.
MOT for octahedral complexes

13. i. Non-degenerate totally symmetric single orbital; s i.e, a1g
ii. Triply degenerate set of p orbitals; px py pz i.e, t1u
iii. Doubly degenerate set of d orbitals; dz2, dx2-y2 i.e, eg
iv. Triply degenerate set of d orbitals; dxy dyz dxz i.e, t2g
General MO diagram of ML6 molecule

14. • Fe is in +2 oxidation state.
• Fe (26)= [Ar] 3d6 4s2
Fe2+ = [Ar] 3d6 4s0
• There are 18 electrons in all, two from each
water molecule and six from Fe2+ ion.
• The 1st twelve electrons are placed in lower six
bonding molecular orbitals a1g t1u and eg. The
remaining electrons are placed in the molecular
orbital of next higher energy.
14
Hexaaquo ferrate (II) ion: [Fe(H2O)6]2+

15. Summary
LCAO Method
Valency electrons are considered as particles or
waves.
Application of MOT
Homonuclear and heteronuclear diatomic species.
Combination of orbitals
s-s, p-p, d-d combination of orbitals to form bonding
and antibonding molecular orbitals.
Polyatomic species
C02 AND SF6 molecule.
Rules of LCAO
Rules to decide which atomic orbitals maybe
combined to form molecular orbitals.
Octahedral complexes
ML6 complexes of metals in 1st transition series.

16. 08
 J.D.Lee concise Inorganic Chemistry
 James Huheey
 Principles of Inorganic Chemistry
 Diagrams: from Google
Refrences

17. THANK YOU…