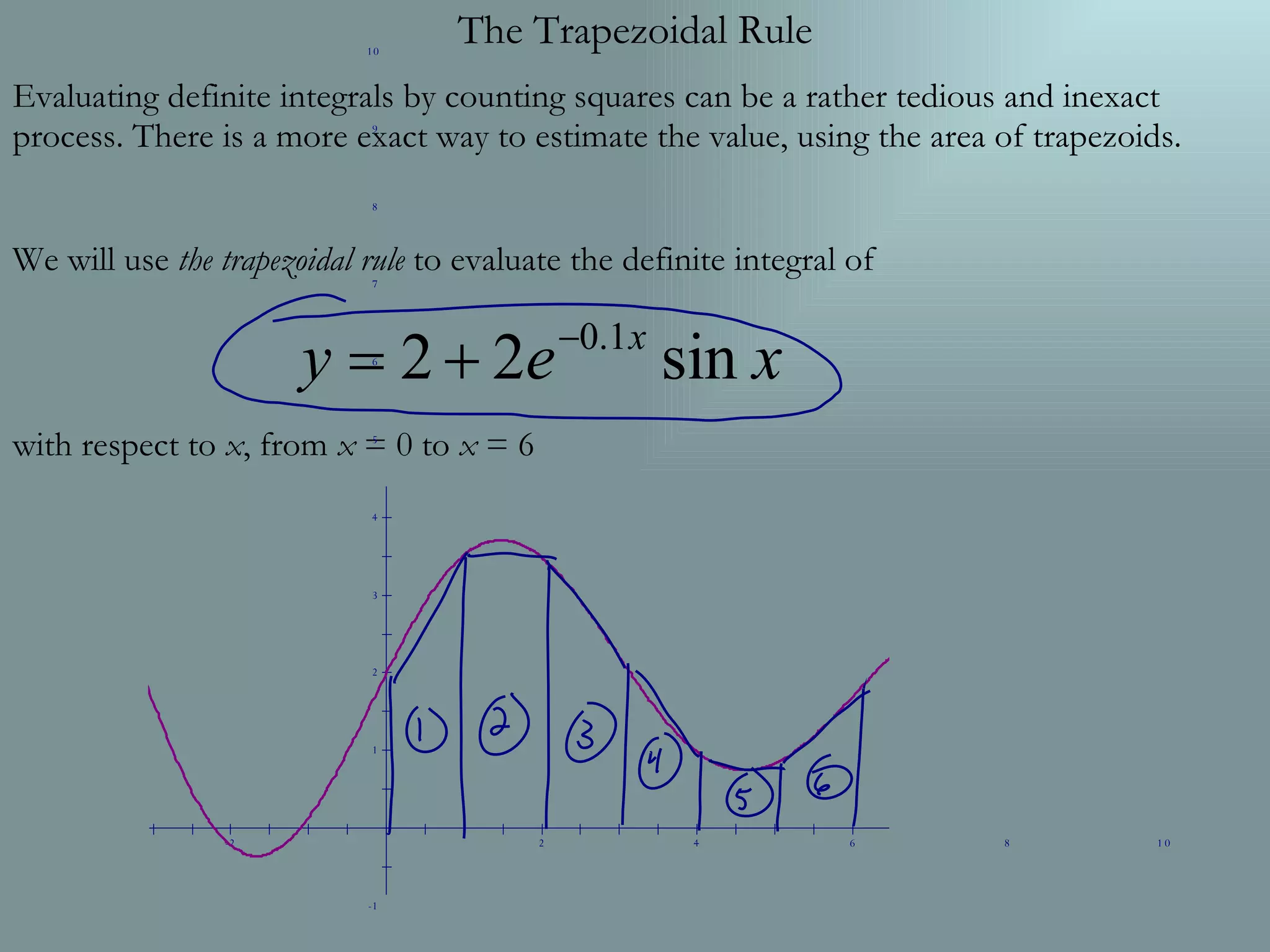
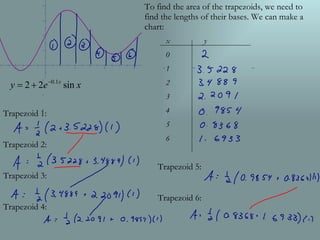
The document discusses using the trapezoidal rule to evaluate definite integrals by approximating the area under a curve between bounds with trapezoids. It explains that the trapezoidal rule is a more exact method than counting squares. To use the rule, the integral bounds are divided into trapezoids, the function is evaluated at the endpoints, and the areas are calculated by multiplying the average base by the height and summing the results, with endpoints weighted by one half.

1. The Trapezoidal Rule Evaluating definite integrals by counting squares can be a rather tedious and inexact process. There is a more exact way to estimate the value, using the area of trapezoids. We will use the trapezoidal rule to evaluate the definite integral of with respect to x , from x = 0 to x = 6

2. x y 0 1 2 3 4 5 6 To find the area of the trapezoids, we need to find the lengths of their bases. We can make a chart: Trapezoid 1: Trapezoid 2: Trapezoid 3: Trapezoid 4: Trapezoid 5: Trapezoid 6:

4. To find a definite integral using the trapezoidal rule: Choose the number of trapezoids you are going to use (the more the better). Evaluate the function at the endpoints of the trapezoids. Add all of the endpoints of the trapezoids, multiplying the ones on the ends by one half. Multiply by the “height” of the trapezoids.