4.10.08 Graphs Of Polynomials
•Download as PPT, PDF•
0 likes•399 views
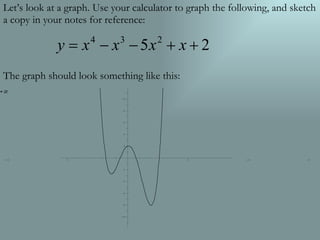
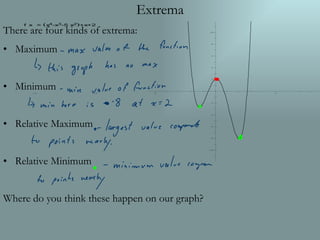
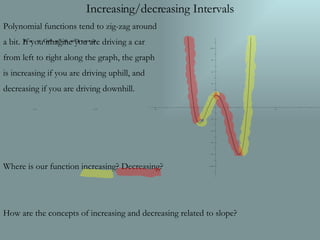
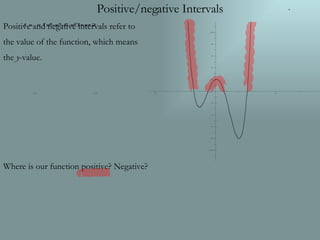
This document discusses key concepts related to graphs of polynomial functions, including: - Extrema (maximum, minimum, relative maximum, relative minimum points) and where they occur on the sample graph - Zeros (x-intercepts) and that the sample function has four zeros - Increasing and decreasing intervals based on the slope, with the function increasing where driving uphill and decreasing where driving downhill - Positive and negative intervals, referring to where the function is positive or negative based on the y-value.
Report
Share
Report
Share
![[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object]](https://image.slidesharecdn.com/41008-graphs-of-polynomials-1207879594555757-9/85/4-10-08-Graphs-Of-Polynomials-1-320.jpg)
Recommended
Theatre Booking System Lesson 3
The document discusses inserting random numbers using the RANDBETWEEN formula to test a theatre booking system model. It explains that the RANDBETWEEN formula generates random numbers between the bottom and top numbers specified, in this case 0 and 4, to represent randomly booked seats. It also provides instructions to enable the Analysis ToolPak add-in if the RANDBETWEEN function does not work initially, and how to copy the formula down and across cells to populate the model with random seat bookings for testing.
Projective plane visualization
The document discusses visualizing the real projective plane by extending the real affine plane to include ideal points and lines. Parallel lines in the affine plane are said to meet at an ideal point on the ideal line outside of the plane. The resulting configuration, with both real and ideal points and lines, is called the real projective plane. Key characteristics include that it contains the affine plane plus the ideal line, and has an infinite number of points and lines.
3D perspective autocad.
3D Drawing discusses different types of perspective drawing techniques and ellipses. There are three main types of perspective drawing: one-point, two-point, and three-point perspective. One-point perspective uses a single vanishing point, two-point uses two vanishing points, and three-point perspective adds complexity with three vanishing points. An ellipse is a circle viewed in perspective, so it follows the same properties as a circle but appears elongated.
Basic SysML Activity Diagram Semantics
The document discusses some basic semantics of SysML activity diagrams including:
- Activity edges can be control flows or object flows to communicate information between actions. Object flows explicitly specify what is being communicated.
- Nodes like merge, decision, join, and fork address OR and AND conditions in activity flows.
- Two activity diagrams are shown with different ways to determine flight range, with no single correct way but representing the intended system design.
Auxiliary views
Auxiliary views are orthographic projections used to show the true size and shape of inclined or oblique surfaces that cannot be fully represented in the standard three views. Auxiliary views are projected from principal views or other auxiliary views. They are used when features need to be shown at their true size for dimensioning or determining measurements like dihedral angles between surfaces. Multiple successive auxiliary views can be created by projecting additional views from existing auxiliary views.
Flexi_Bridge_Chart
Flexi Bridge Chart is a user-friendly and automated Excel add-in that creates flexible bridge charts. It allows users to easily input cell values which are then used to automatically generate colored bridge charts with adjustable check points. All calculations are done programmatically through macro coding to avoid human error and provide flexibility to handle negative and positive values.
Day 6 examples
This document discusses numerical integration techniques for approximating integrals, including left- and right-hand sums, midpoint sums, and trapezoid sums. It explains that midpoint sums and trapezoid sums reduce the error of approximations and provides formulas for estimating the error bounds of these methods based on the second derivative of the function. The document also includes questions about selecting the number of subintervals needed to achieve a given error tolerance using trapezoid or midpoint sums.
Class 12 presentation
This document provides information about a 2D essentials class taught by Laura Gerold from January 18, 2012 to May 16, 2012. It includes reminders about the final project due date of May 9th and final exam on May 16th. It also provides an opportunity for extra credit by submitting a question for the final exam by May 2nd. The document discusses mixing up groups, homework problems, section views, auxiliary views, and examples of primary and secondary auxiliary views.
Recommended
Theatre Booking System Lesson 3
The document discusses inserting random numbers using the RANDBETWEEN formula to test a theatre booking system model. It explains that the RANDBETWEEN formula generates random numbers between the bottom and top numbers specified, in this case 0 and 4, to represent randomly booked seats. It also provides instructions to enable the Analysis ToolPak add-in if the RANDBETWEEN function does not work initially, and how to copy the formula down and across cells to populate the model with random seat bookings for testing.
Projective plane visualization
The document discusses visualizing the real projective plane by extending the real affine plane to include ideal points and lines. Parallel lines in the affine plane are said to meet at an ideal point on the ideal line outside of the plane. The resulting configuration, with both real and ideal points and lines, is called the real projective plane. Key characteristics include that it contains the affine plane plus the ideal line, and has an infinite number of points and lines.
3D perspective autocad.
3D Drawing discusses different types of perspective drawing techniques and ellipses. There are three main types of perspective drawing: one-point, two-point, and three-point perspective. One-point perspective uses a single vanishing point, two-point uses two vanishing points, and three-point perspective adds complexity with three vanishing points. An ellipse is a circle viewed in perspective, so it follows the same properties as a circle but appears elongated.
Basic SysML Activity Diagram Semantics
The document discusses some basic semantics of SysML activity diagrams including:
- Activity edges can be control flows or object flows to communicate information between actions. Object flows explicitly specify what is being communicated.
- Nodes like merge, decision, join, and fork address OR and AND conditions in activity flows.
- Two activity diagrams are shown with different ways to determine flight range, with no single correct way but representing the intended system design.
Auxiliary views
Auxiliary views are orthographic projections used to show the true size and shape of inclined or oblique surfaces that cannot be fully represented in the standard three views. Auxiliary views are projected from principal views or other auxiliary views. They are used when features need to be shown at their true size for dimensioning or determining measurements like dihedral angles between surfaces. Multiple successive auxiliary views can be created by projecting additional views from existing auxiliary views.
Flexi_Bridge_Chart
Flexi Bridge Chart is a user-friendly and automated Excel add-in that creates flexible bridge charts. It allows users to easily input cell values which are then used to automatically generate colored bridge charts with adjustable check points. All calculations are done programmatically through macro coding to avoid human error and provide flexibility to handle negative and positive values.
Day 6 examples
This document discusses numerical integration techniques for approximating integrals, including left- and right-hand sums, midpoint sums, and trapezoid sums. It explains that midpoint sums and trapezoid sums reduce the error of approximations and provides formulas for estimating the error bounds of these methods based on the second derivative of the function. The document also includes questions about selecting the number of subintervals needed to achieve a given error tolerance using trapezoid or midpoint sums.
Class 12 presentation
This document provides information about a 2D essentials class taught by Laura Gerold from January 18, 2012 to May 16, 2012. It includes reminders about the final project due date of May 9th and final exam on May 16th. It also provides an opportunity for extra credit by submitting a question for the final exam by May 2nd. The document discusses mixing up groups, homework problems, section views, auxiliary views, and examples of primary and secondary auxiliary views.
Putting Web Into Native App
This document discusses the evolution of mobile apps from native to web apps. It notes that early on, most apps were developed natively for each mobile platform, but that the trend is shifting to web apps that can work cross-platform using technologies like HTML5. The document outlines three strategies companies can take for building web apps: 1) using a native wrapper with a web view, 2) using a HTML5 framework, or 3) using a cross-platform framework. It also provides examples of companies taking these approaches and the benefits of web apps over native apps.
UCM 5
This document defines and provides examples of uniform circular motion (UCM). UCM occurs when an object moves in a circular path at a constant speed. Centripetal force is the force directing an object towards the center and causing UCM by overcoming the object's inertia. Examples include a car turning a corner, a person on a spinning ride, a ball on a string, and satellites orbiting bodies. The document also provides steps for solving UCM problems using formulas for centripetal force, centripetal acceleration, and velocity, demonstrating the process through a sample problem of calculating the centripetal force on a plane circling a radius.
3rd Quarter Research Project
This document outlines the requirements for a 3rd quarter research project for students related to Sea Camp. Students must research a topic approved by the teacher, complete a keyword outline using at least 5 sources, write 10 multiple choice test questions, and create a presentation using a format like PowerPoint, book, or video. Topics include various aspects of coral reefs and marine life. Source citations and a bibliography are required. Projects are due in phases with topics due first, then outlines, presentations for preview, and final projects. Projects are graded based on the quality of the product, presentation, bibliography, and outline.
CRM als Universele Stekkerdoos (Pecha kucha Open Coffee)
In deze korte presentatie wordt toegelicht op welke wijze CRM kan worden als een platform voor applicatie-integratie.
3.11.08 Geometric Series1
The document discusses geometric series and how to find the general formula for the sum of a geometric series. It provides an example of a geometric sequence where the ratio between successive terms is constant at 2. The document also explains how to derive the general formula for the nth partial sum of a geometric sequence by setting up equations for the first few terms and then subtracting the equations.
The Dutch ODF Policy in Retrospect
In this presentation Fabrice Mous shares his experiences as former ODF project lead for the Dutch government and gives an honest view on the implementation of this policy. This presentation is meant as a lessons learned session and the experiences are to be considered as a set of recommendations.
Kostenbesparende Werkpaarden
Met de technologische ontwikkelingen en de toenemende wensen van gebruikers blijven de kosten voor datamanagement continue stijgen. Deze presentatie toont op welke wijze met open source software kostenbesparingen mogelijk zijn op uw datamanagement. Deze presentatie schetst de databasemarkt en het huidige gebruik van databases en waar nu exact de kansen liggen om kosten te besparen met open source databases. Deze presentatie geeft specifieke aandacht aan de business case waarbij een scherpe vergelijking zal worden neergezet van de verschillende databaseproducten.
Deze presentatie is gegeven op de beurs "Overheid en ICT 2010".
SYSADMIN TNG
Deze presentatie geeft een uiteenzetting over het beroep van systeembeheerder, de meerwaarde van certificering voor de IT-professional, de opkomst van open-source software en Linux en de werking van het certificeringstraject van het Linux Professional Institute.
2007 Oct To Dec
This document provides updates on various events at an orphanage, including a new mother named Paulina, a family moving into a new home, celebrating birthdays and holidays, children participating in activities like field day, soccer, art classes, and more. It concludes by thanking supporters for their ongoing prayers and financial support of the orphanage.
Solving Linear Equations
This document provides an overview of linear equations and how to solve them. Linear equations only contain variables raised to the first power and can be more complicated than early math problems involving addition. To solve linear equations, the same operations are performed on both sides of the equation until no operations remain and the variable is isolated on one side in its solution. An example problem walks through the steps of subtracting 6 from both sides to isolate x and reveal that the solution is x = -9.
Congreso Internet3.0 Alicante 2013
La Unión Europea ha acordado un paquete de sanciones contra Rusia por su invasión de Ucrania. Las sanciones incluyen restricciones a las transacciones con bancos rusos clave y la prohibición de la venta de aviones y equipos a Rusia. Los líderes de la UE esperan que las sanciones aumenten la presión económica sobre Rusia y la disuadan de continuar su agresión contra Ucrania.
2.20.08 Probability Distributions
This document discusses probability distributions when rolling a pair of dice. There are 36 possible combinations of numbers from 1 to 6 that can be rolled, and 11 possible sums. A probability distribution assigns the probability of each possible event, with the event as the independent variable and its probability as the dependent variable. The document then tests the accuracy of these theoretical probabilities by recording the actual frequency and percentage of each sum occurring over 50 rolls.
Marketing plan
The document summarizes Greece's plan to promote technology companies from Greece at the 2014 Mobile World Congress (MWC'14) in Barcelona. It discusses recruiting a strong team of over 15 experts to handle marketing, sales, logistics and media. Key aspects of the marketing plan include promoting Greece's presence in Africa and the Mediterranean, giving away tickets to incentivize visitors, and hosting a technology cruise and web radio station at their pavilion. The document outlines how companies, startups, academia, sponsors and press can participate and provides a timeline leading up to and during the event.
How to make sales when you dont like selling 2
New Seminar and Workshop based on the successful book of the same name. Designed to help business owners and sales people, particularly those who find selling challenging.
I-9 Compliance
I-9 Compliance is often overlooked by many companies hiring foreign workers. It is important to keep in compliance of this legal requirement. Watch this slide-show to know WHY and HOW!
VAWA Self Petitioning
Violence Against Women Act (1995) is a provision of the Immigration and Nationality Act, codified in Section 204(a).
Under VAWA, battered spouses or children may self-petition for lawful permanent residence under the Act, without the batterer’s knowledge
Graphmatica an overview
This document provides a quick start guide for using the Graphmatica software to draw mathematical graphs and perform numerical and calculus operations on functions. It outlines how to change display settings like scale and colors, plot multiple graphs simultaneously, trace and find coordinates of points, zoom in and out, mark points, add labels, copy and save graphs, erase graphs, and use advanced calculus features to find roots, slopes, derivatives and integrals of functions graphed in the software.
Point free or die - tacit programming in Haskell and beyond
I really liked Amar Shah's talk on point-free style as a tool for producing tacit code which communicates better because it is quiet and so easier to understand. https://www.youtube.com/watch?v=seVSlKazsNk
This slide deck is my effort to capture the content of the talk in a way that can aid its consumption, digestion and retention.
Download for better quality.
More Related Content
Viewers also liked
Putting Web Into Native App
This document discusses the evolution of mobile apps from native to web apps. It notes that early on, most apps were developed natively for each mobile platform, but that the trend is shifting to web apps that can work cross-platform using technologies like HTML5. The document outlines three strategies companies can take for building web apps: 1) using a native wrapper with a web view, 2) using a HTML5 framework, or 3) using a cross-platform framework. It also provides examples of companies taking these approaches and the benefits of web apps over native apps.
UCM 5
This document defines and provides examples of uniform circular motion (UCM). UCM occurs when an object moves in a circular path at a constant speed. Centripetal force is the force directing an object towards the center and causing UCM by overcoming the object's inertia. Examples include a car turning a corner, a person on a spinning ride, a ball on a string, and satellites orbiting bodies. The document also provides steps for solving UCM problems using formulas for centripetal force, centripetal acceleration, and velocity, demonstrating the process through a sample problem of calculating the centripetal force on a plane circling a radius.
3rd Quarter Research Project
This document outlines the requirements for a 3rd quarter research project for students related to Sea Camp. Students must research a topic approved by the teacher, complete a keyword outline using at least 5 sources, write 10 multiple choice test questions, and create a presentation using a format like PowerPoint, book, or video. Topics include various aspects of coral reefs and marine life. Source citations and a bibliography are required. Projects are due in phases with topics due first, then outlines, presentations for preview, and final projects. Projects are graded based on the quality of the product, presentation, bibliography, and outline.
CRM als Universele Stekkerdoos (Pecha kucha Open Coffee)
In deze korte presentatie wordt toegelicht op welke wijze CRM kan worden als een platform voor applicatie-integratie.
3.11.08 Geometric Series1
The document discusses geometric series and how to find the general formula for the sum of a geometric series. It provides an example of a geometric sequence where the ratio between successive terms is constant at 2. The document also explains how to derive the general formula for the nth partial sum of a geometric sequence by setting up equations for the first few terms and then subtracting the equations.
The Dutch ODF Policy in Retrospect
In this presentation Fabrice Mous shares his experiences as former ODF project lead for the Dutch government and gives an honest view on the implementation of this policy. This presentation is meant as a lessons learned session and the experiences are to be considered as a set of recommendations.
Kostenbesparende Werkpaarden
Met de technologische ontwikkelingen en de toenemende wensen van gebruikers blijven de kosten voor datamanagement continue stijgen. Deze presentatie toont op welke wijze met open source software kostenbesparingen mogelijk zijn op uw datamanagement. Deze presentatie schetst de databasemarkt en het huidige gebruik van databases en waar nu exact de kansen liggen om kosten te besparen met open source databases. Deze presentatie geeft specifieke aandacht aan de business case waarbij een scherpe vergelijking zal worden neergezet van de verschillende databaseproducten.
Deze presentatie is gegeven op de beurs "Overheid en ICT 2010".
SYSADMIN TNG
Deze presentatie geeft een uiteenzetting over het beroep van systeembeheerder, de meerwaarde van certificering voor de IT-professional, de opkomst van open-source software en Linux en de werking van het certificeringstraject van het Linux Professional Institute.
2007 Oct To Dec
This document provides updates on various events at an orphanage, including a new mother named Paulina, a family moving into a new home, celebrating birthdays and holidays, children participating in activities like field day, soccer, art classes, and more. It concludes by thanking supporters for their ongoing prayers and financial support of the orphanage.
Solving Linear Equations
This document provides an overview of linear equations and how to solve them. Linear equations only contain variables raised to the first power and can be more complicated than early math problems involving addition. To solve linear equations, the same operations are performed on both sides of the equation until no operations remain and the variable is isolated on one side in its solution. An example problem walks through the steps of subtracting 6 from both sides to isolate x and reveal that the solution is x = -9.
Congreso Internet3.0 Alicante 2013
La Unión Europea ha acordado un paquete de sanciones contra Rusia por su invasión de Ucrania. Las sanciones incluyen restricciones a las transacciones con bancos rusos clave y la prohibición de la venta de aviones y equipos a Rusia. Los líderes de la UE esperan que las sanciones aumenten la presión económica sobre Rusia y la disuadan de continuar su agresión contra Ucrania.
2.20.08 Probability Distributions
This document discusses probability distributions when rolling a pair of dice. There are 36 possible combinations of numbers from 1 to 6 that can be rolled, and 11 possible sums. A probability distribution assigns the probability of each possible event, with the event as the independent variable and its probability as the dependent variable. The document then tests the accuracy of these theoretical probabilities by recording the actual frequency and percentage of each sum occurring over 50 rolls.
Marketing plan
The document summarizes Greece's plan to promote technology companies from Greece at the 2014 Mobile World Congress (MWC'14) in Barcelona. It discusses recruiting a strong team of over 15 experts to handle marketing, sales, logistics and media. Key aspects of the marketing plan include promoting Greece's presence in Africa and the Mediterranean, giving away tickets to incentivize visitors, and hosting a technology cruise and web radio station at their pavilion. The document outlines how companies, startups, academia, sponsors and press can participate and provides a timeline leading up to and during the event.
How to make sales when you dont like selling 2
New Seminar and Workshop based on the successful book of the same name. Designed to help business owners and sales people, particularly those who find selling challenging.
I-9 Compliance
I-9 Compliance is often overlooked by many companies hiring foreign workers. It is important to keep in compliance of this legal requirement. Watch this slide-show to know WHY and HOW!
VAWA Self Petitioning
Violence Against Women Act (1995) is a provision of the Immigration and Nationality Act, codified in Section 204(a).
Under VAWA, battered spouses or children may self-petition for lawful permanent residence under the Act, without the batterer’s knowledge
Viewers also liked (20)
CRM als Universele Stekkerdoos (Pecha kucha Open Coffee)
CRM als Universele Stekkerdoos (Pecha kucha Open Coffee)
Similar to 4.10.08 Graphs Of Polynomials
Graphmatica an overview
This document provides a quick start guide for using the Graphmatica software to draw mathematical graphs and perform numerical and calculus operations on functions. It outlines how to change display settings like scale and colors, plot multiple graphs simultaneously, trace and find coordinates of points, zoom in and out, mark points, add labels, copy and save graphs, erase graphs, and use advanced calculus features to find roots, slopes, derivatives and integrals of functions graphed in the software.
Point free or die - tacit programming in Haskell and beyond
I really liked Amar Shah's talk on point-free style as a tool for producing tacit code which communicates better because it is quiet and so easier to understand. https://www.youtube.com/watch?v=seVSlKazsNk
This slide deck is my effort to capture the content of the talk in a way that can aid its consumption, digestion and retention.
Download for better quality.
Linear & Exponential Equations/Functions
This document provides an overview of linear and exponential equations and functions that will be covered in an Algebra II class. It introduces key concepts for both types of equations, including slope and y-intercept for linear equations, and base and exponent for exponential equations. Common forms of linear equations like standard form and slope-intercept form are described. Exponential growth and decay functions are defined. Students will learn to identify, write, and solve different types of linear and exponential equations and distinguish between linear and exponential functions.
Miscellneous functions
This document discusses various types of functions including compositions of functions, even and odd functions, and increasing, decreasing, and constant functions. It begins with a review of what a function is and provides examples of adding, subtracting, multiplying, and dividing functions. It then explains how to determine if a function is increasing, decreasing, or constant based on its graph. Next, it defines even and odd functions and provides examples of identifying these algebraically. The document goes on to explain what a composition of functions is and provides examples of evaluating compositions both algebraically and graphically. It also discusses decomposing functions and finding the domains of composite functions algebraically.
2. mathematical functions in excel
Mathematical functions in Excel are used to perform arithmetic operations like sum, average, count, max, min. The SUM function adds the values within a cell range. For example, SUM(C1:C3)=15 adds the values in cells C1 through C3. The AVERAGE function calculates the average of a range of cells. COUNT counts the number of cells that contain numbers. Other common functions include ROUND, RAND, MOD, INT, ABS, ARABIC, and CEILING.MATH.
Tutorial: Photoshop Paths Explained
Learn the basics of vector paths in Photoshop, including line segments, anchor points, and
path components.
Intro to exponents
This document introduces exponents and explains what they are. Exponents tell us to take a number called the base and multiply it by itself a certain number of times, represented by the exponent. The base is written normally sized and the exponent is written smaller above the base. Exponents show repeated multiplication, with the exponent indicating how many times the base is multiplied. Examples are provided to illustrate exponents and their notation.
Sift logo creation analysis
Omar Rasoul created a logo for S.I.F.T in 7 steps. He began by using ellipses tools to make a large red circle with a white inner circle for the background. In step two, he added the organization's name in varying letter sizes to reflect the erratic nature of teen issues. Step three added newspaper clippings as a backdrop. Step four merged all layers. Step five isolated a hand image. Step six applied a filter to soften the hand. The final step ordered all layers to complete the logo with a newsprint backdrop and hand image centered in the circles.
Toolkit functions preview
This document discusses parent functions and their transformations, as well as toolkit functions that students should know for pre-calculus. It lists linear, square root, quadratic, cubic, rational, logarithmic, exponential, absolute value, and quartic functions as toolkit functions. For each function, students should understand properties like the graph, domain and range, intervals of increase/decrease, extrema, intercepts, end behaviors, asymptotes, symmetry, and continuity. An example is provided for the quartic function.
Spreadsheets for developers
Spreadsheets are often dismissed by developers for not being "proper programming" but that is not true. Since I have shown that spreadsheets are Turing complete, you have no excuse to diss them any longer. In this session, I will implement various algorithms in Excel to show you its power and elegance. After all, spreadsheets are 'live' and functional, so they have everything going for them! Furthermore they are very fit for TDD and rapid prototyping.
Don't fight spreadsheets any longer, but learn to love them.
Numerical analysis using Scilab: Error analysis and propagation
This tutorial provides a collection of numerical examples and advises on error analysis and its propagation. All examples are developed in Scilab.
Data Presentation
The document provides guidance on how to achieve a level 3 on a GCSE coursework for data presentation. It discusses using more complex techniques like graphs, statistical analysis, tables, and pictograms to present data. It emphasizes choosing techniques that are appropriate for the investigation and providing clear organization and labeling. Specific tips are provided for different graph types, common mistakes to avoid, and how to properly construct pictograms using accurate scales and keys. Examples of good and bad pictograms are included.
Data Science - Part XV - MARS, Logistic Regression, & Survival Analysis
This lecture provides an overview on extending the regression concepts brought forth in previous lectures. We will start off by going through a broad overview of the Multivariate Adaptive Regression Splines Algorithm, Logistic Regression, and then explore the Survival Analysis. The presentation will culminate with a real world example on how these techniques can be used in the US criminal justice system.
Lecture 05.pptx
Operators are symbols that perform operations on values in Python. There are different types of operators such as arithmetic, assignment, comparison, and logical operators. The order that operators are evaluated depends on their priority and whether they have left-sided or right-sided binding. Parentheses can be used to change the natural order of evaluations in expressions. Floating point numbers may result in small rounding errors due to limitations in how computers store numeric values.
Unit 5
The document provides information about fractions, percents, and circle graphs. It includes steps for adding fractions, comparing fractions, converting between fractions and percents, drawing and interpreting circle graphs, and finding equivalent fractions. Interactive games and worksheets are referenced throughout to provide additional practice opportunities.
intro to Pattern
This document discusses different methods for representing patterns of tables and seating arrangements mathematically, including drawing the pattern, using a table, using a graph, and developing a mathematical model. It explains that a mathematical model can be created from any of these previous representation methods using the formula for a linear relationship, Y = Mx + C, where M is the slope and C is the y-intercept. An example of using this process to model a pattern of increasing numbers of tables and seats is provided.
Lập trình C
The document provides an overview of a C programming course, including:
1) The course will teach programming C elegantly and writing good algorithms, without fancy graphics.
2) Programming is useful for applying math concepts to the real world through simulation.
3) C was chosen as it is small, common, stable, and quick-running, forming the basis for many languages.
4) The document defines some programming terminology and covers basic C programming concepts like variables, functions, and debugging techniques.
An%20Intermediate%20Google%20SketchUp%20Tutorial%20-%20Part%203
The document is an intermediate tutorial for Google SketchUp. It introduces Bezier curves, which allow for complex shapes. A Ruby script called bezierspline.zip must be downloaded and installed to access these tools. There are different types of Bezier curves - classic, polyline, uniform B-spline, and cubic Bezier. The document compares each type and determines the cubic Bezier curve is the most predictable and controllable. It then demonstrates using the cubic Bezier curve tool to model the profile of an office table edge.
An%20Intermediate%20Google%20SketchUp%20Tutorial%20-%20Part%203
The document is an intermediate tutorial for Google SketchUp. It introduces Bezier curves, which allow for complex shapes. A Ruby script called bezierspline.zip adds Bezier curve tools. There are different types of Bezier curves - classic, polyline, uniform B-spline, and cubic Bezier. The document compares each type using a sample shape and finds the cubic Bezier curve the most predictable and controllable. It then demonstrates using the cubic Bezier curve to model the profile of an office table edge.
GUI based Face detection using Viola-Jones algorithm in MATLAB.
The document discusses the Viola-Jones face detection algorithm. It outlines how the algorithm uses Haar-like features and an integral image to quickly detect faces in images. The Viola-Jones algorithm searches an image with sliding boxes and detects Haar-like features within each box, such as edges, lines, and four-sided shapes. An integral image allows for fast calculation of Haar-like feature values by summing pixel values within regions. Together, Haar-like features and the integral image allow the Viola-Jones algorithm to efficiently detect the presence of faces in images.
Similar to 4.10.08 Graphs Of Polynomials (20)
Point free or die - tacit programming in Haskell and beyond
Point free or die - tacit programming in Haskell and beyond
Numerical analysis using Scilab: Error analysis and propagation
Numerical analysis using Scilab: Error analysis and propagation
Data Science - Part XV - MARS, Logistic Regression, & Survival Analysis
Data Science - Part XV - MARS, Logistic Regression, & Survival Analysis
An%20Intermediate%20Google%20SketchUp%20Tutorial%20-%20Part%203
An%20Intermediate%20Google%20SketchUp%20Tutorial%20-%20Part%203
An%20Intermediate%20Google%20SketchUp%20Tutorial%20-%20Part%203
An%20Intermediate%20Google%20SketchUp%20Tutorial%20-%20Part%203
GUI based Face detection using Viola-Jones algorithm in MATLAB.
GUI based Face detection using Viola-Jones algorithm in MATLAB.
More from chrismac47
Lesson 2-5
The document compares exponential and linear models. Exponential models exhibit constant percentage change determined by the growth factor b, while linear models show constant increase/decrease set by the slope m. Exponential equations can be determined from a single point, unlike linear equations which require two points to find the parameters m and b. The document demonstrates finding the exponential equation for two given points (2,6) and (4,10) by setting up equations and dividing them to isolate the growth factor b.
Lesson 2 1
The document discusses functions and function notation. It defines a function as a special type of relation where each element of the independent variable is paired with exactly one element of the dependent variable. It provides examples of different ways to represent functions, including coordinate graphs, symbolic rules, and ordered pairs. The document also discusses evaluating functions, the domain and range of functions, and identifies whether certain relations are functions or not.
Lesson 2 2
This document discusses using linear models to summarize relationships in data. It provides examples of how astronomers use a linear model called Hubble's Constant to describe the relationship between galaxies' distances and velocities. It introduces the correlation coefficient r as a measure of how closely data points fit a linear model or line of best fit, with r values closer to 1 or -1 indicating a stronger linear correlation. Some scatter plots with r values are shown to illustrate what different r values look like. The document explains the formula for calculating r and encourages interpreting what the various parts of the formula represent. It then poses fitting a line of best fit to a set of sample x and y data values as an example.
Section 2 3 (1)
This document provides 5 calculus limits to evaluate: 1) as x approaches 0, 2) as x approaches infinity, 3) as x approaches -1, 4) as x approaches 0, and 5) as x approaches infinity.
Section 2.5 (2)
This document discusses expanding the concept of limits to include infinite limits, where the variable approaches infinity. It introduces the idea of analyzing functions where the variable gets infinitely large and the limit potentially reaches infinity as well. The example function raises the question of how to analyze its behavior as the variable increases without bound.
Section 2.4
This document discusses continuity and discontinuity in functions. It defines a function as continuous at a point c if the left and right hand limits are the same as x approaches c. A function is discontinuous if the left and right limits do not match up. Examples are given of different types of discontinuities like removable discontinuities.
Lesson 1 7 (3)
Variance and standard deviation are measures of spread used to describe the shape of distributions associated with the mean. While two distributions may have the same mean, their variance and standard deviation can show that they have very different shapes. To calculate variance and standard deviation, you first find the deviation of each value from the mean, square the deviations, and sum them. You then divide the sum by n-1 to get the variance, and take the square root of the variance to find the standard deviation.
Section 1-5
The document discusses the concept of limits in calculus, including the formal definition of a limit as the value a function approaches as the input gets arbitrarily close to a given number. It provides examples of evaluating limits graphically and algebraically, such as determining the limit of a function as x approaches 3 is 6, even though the function is undefined at x=3 due to a removable discontinuity. The document also discusses using graphs to identify different types of discontinuities and limits.
Section 1-4 -- Trapezoid Rule
The document discusses using the trapezoidal rule to evaluate definite integrals by approximating the area under a curve between bounds with trapezoids. It explains that the trapezoidal rule is a more exact method than counting squares. To use the rule, the integral bounds are divided into trapezoids, the function is evaluated at the endpoints, and the areas are calculated by multiplying the average base by the height and summing the results, with endpoints weighted by one half.
Lesson 1-4 -- Five Number Summary
The document discusses the five number summary, which includes the minimum, first quartile, median, third quartile, and maximum values. It provides an example of the heights of a basketball team, calculates their five number summary and interquartile range, and discusses how outliers can be identified using 1.5 times the interquartile range.
Section 1-3 -- Definite Integrals
The document discusses using integrals to calculate distance traveled based on a velocity-time graph. It explains that the area under the graph between two times represents the distance traveled during that interval. Specifically, it asks the reader to:
1) Find the velocity between 30-50 seconds from the given graph and explain why the distance can be found from the rectangular area.
2) Count the squares and find the distance traveled from 0-20 seconds by finding the area under the curved graph.
3) Estimate the definite integral of a function representing a football's cross-sectional area to find its total volume.
Lesson 1-3
The document discusses different measures of central tendency, including the mean and median. It introduces the concept of using sigma notation to simplify writing out long sums, such as when calculating the mean of a data set. It provides an example of entree prices from a restaurant and encourages writing out the formula to calculate the mean using sigma notation.
Section 1-2
This document discusses functions, their derivatives, and rates of change. It introduces the concept of the derivative as the instantaneous rate of change of a function. It then asks the reader to sketch and describe different types of functions without a calculator. It provides a sample graph showing sections that are increasing, decreasing, or neither, and asks the reader to identify these sections and determine where the rate of change is more or less quick.
Lesson 1 2
A stemplot is a method to display data by splitting each number into a stem and leaf, with the ones digit as the leaf and other digits as the stem. It allows comparison of two data sets side by side. A dotplot displays the frequency of data values and is useful when the data is categorical. It may not be suitable to display continuous numeric data like golf scores.
5.12.08 Advanced Factoring1
Factoring by grouping allows factoring out the greatest common factor from some but not all terms of a polynomial, which can make the entire factorization easier. This technique can be used to factor difficult quadratic trinomials. Examples are provided to illustrate factoring by grouping.
5.6.08 Fundamental Theorem Of Algebra1
The fundamental theorem of algebra states that any polynomial of degree greater than 1 with complex coefficients has at least one complex zero. A related theorem is that a polynomial of degree n has at most n zeros. Another theorem is that a polynomial of degree greater than 1 with complex coefficients has exactly n complex zeros counting multiplicities.
4.14.08 Finding Polynomial Models1 2
The document discusses finding polynomial models to describe patterns like triangular numbers and tetrahedral numbers. It explains that a polynomial difference theorem can be used to find the polynomial formula for functions where the differences between successive values form a known pattern. Specifically, if the fourth differences are constant, the function is a fourth degree polynomial that can be determined by plugging known points into the general cubic polynomial formula.
4.9.08 Polynomial Models3
The document discusses polynomial models and volume equations. It provides an example of a box made from cardboard where squares are cut from the corners and the sides are folded up. An equation is written for the volume of the box in terms of x, which is a third degree polynomial. A polynomial's degree is the maximum number of variables being multiplied. The standard form of a polynomial of degree n is also discussed. The volume of the cardboard box is written in standard form. A polynomial with more than one variable, like (x+y)^4, has a degree of 4.
4.3.08 Binomial Prob 1
The document discusses binomial probabilities and permutations for repeated independent trials with two possible outcomes. It asks what the probability is of getting 4 or more blues when spinning a spinner 6 times, and the probability of getting 3 or more reds in 6 spins. It introduces the binomial probability theorem for calculating these probabilities.
4.1.08 Pascals Triangle2
Pascal's Triangle is an array of numbers arranged in triangular form where each number is derived from adding the two numbers directly above it. To generate the triangle, a chart is made where the terms are found by taking the binomial coefficients of n over r, and properties include that each row has one more term than the previous row and the first and last terms of each row are always 1.
More from chrismac47 (20)
Recently uploaded
National Security Agency - NSA mobile device best practices
Threats to mobile devices are more prevalent and increasing in scope and complexity. Users of mobile devices desire to take full advantage of the features
available on those devices, but many of the features provide convenience and capability but sacrifice security. This best practices guide outlines steps the users can take to better protect personal devices and information.
TrustArc Webinar - 2024 Global Privacy Survey
How does your privacy program stack up against your peers? What challenges are privacy teams tackling and prioritizing in 2024?
In the fifth annual Global Privacy Benchmarks Survey, we asked over 1,800 global privacy professionals and business executives to share their perspectives on the current state of privacy inside and outside of their organizations. This year’s report focused on emerging areas of importance for privacy and compliance professionals, including considerations and implications of Artificial Intelligence (AI) technologies, building brand trust, and different approaches for achieving higher privacy competence scores.
See how organizational priorities and strategic approaches to data security and privacy are evolving around the globe.
This webinar will review:
- The top 10 privacy insights from the fifth annual Global Privacy Benchmarks Survey
- The top challenges for privacy leaders, practitioners, and organizations in 2024
- Key themes to consider in developing and maintaining your privacy program
Communications Mining Series - Zero to Hero - Session 1
This session provides introduction to UiPath Communication Mining, importance and platform overview. You will acquire a good understand of the phases in Communication Mining as we go over the platform with you. Topics covered:
• Communication Mining Overview
• Why is it important?
• How can it help today’s business and the benefits
• Phases in Communication Mining
• Demo on Platform overview
• Q/A
Uni Systems Copilot event_05062024_C.Vlachos.pdf
Unlocking Productivity: Leveraging the Potential of Copilot in Microsoft 365, a presentation by Christoforos Vlachos, Senior Solutions Manager – Modern Workplace, Uni Systems
20240609 QFM020 Irresponsible AI Reading List May 2024
Everything I found interesting about the irresponsible use of machine intelligence in May 2024
Pushing the limits of ePRTC: 100ns holdover for 100 days
At WSTS 2024, Alon Stern explored the topic of parametric holdover and explained how recent research findings can be implemented in real-world PNT networks to achieve 100 nanoseconds of accuracy for up to 100 days.
Enchancing adoption of Open Source Libraries. A case study on Albumentations.AI
Enchancing adoption of Open Source Libraries. A case study on Albumentations.AIVladimir Iglovikov, Ph.D.
Presented by Vladimir Iglovikov:
- https://www.linkedin.com/in/iglovikov/
- https://x.com/viglovikov
- https://www.instagram.com/ternaus/
This presentation delves into the journey of Albumentations.ai, a highly successful open-source library for data augmentation.
Created out of a necessity for superior performance in Kaggle competitions, Albumentations has grown to become a widely used tool among data scientists and machine learning practitioners.
This case study covers various aspects, including:
People: The contributors and community that have supported Albumentations.
Metrics: The success indicators such as downloads, daily active users, GitHub stars, and financial contributions.
Challenges: The hurdles in monetizing open-source projects and measuring user engagement.
Development Practices: Best practices for creating, maintaining, and scaling open-source libraries, including code hygiene, CI/CD, and fast iteration.
Community Building: Strategies for making adoption easy, iterating quickly, and fostering a vibrant, engaged community.
Marketing: Both online and offline marketing tactics, focusing on real, impactful interactions and collaborations.
Mental Health: Maintaining balance and not feeling pressured by user demands.
Key insights include the importance of automation, making the adoption process seamless, and leveraging offline interactions for marketing. The presentation also emphasizes the need for continuous small improvements and building a friendly, inclusive community that contributes to the project's growth.
Vladimir Iglovikov brings his extensive experience as a Kaggle Grandmaster, ex-Staff ML Engineer at Lyft, sharing valuable lessons and practical advice for anyone looking to enhance the adoption of their open-source projects.
Explore more about Albumentations and join the community at:
GitHub: https://github.com/albumentations-team/albumentations
Website: https://albumentations.ai/
LinkedIn: https://www.linkedin.com/company/100504475
Twitter: https://x.com/albumentationsA tale of scale & speed: How the US Navy is enabling software delivery from l...
Rapid and secure feature delivery is a goal across every application team and every branch of the DoD. The Navy’s DevSecOps platform, Party Barge, has achieved:
- Reduction in onboarding time from 5 weeks to 1 day
- Improved developer experience and productivity through actionable findings and reduction of false positives
- Maintenance of superior security standards and inherent policy enforcement with Authorization to Operate (ATO)
Development teams can ship efficiently and ensure applications are cyber ready for Navy Authorizing Officials (AOs). In this webinar, Sigma Defense and Anchore will give attendees a look behind the scenes and demo secure pipeline automation and security artifacts that speed up application ATO and time to production.
We will cover:
- How to remove silos in DevSecOps
- How to build efficient development pipeline roles and component templates
- How to deliver security artifacts that matter for ATO’s (SBOMs, vulnerability reports, and policy evidence)
- How to streamline operations with automated policy checks on container images
Cosa hanno in comune un mattoncino Lego e la backdoor XZ?
ABSTRACT: A prima vista, un mattoncino Lego e la backdoor XZ potrebbero avere in comune il fatto di essere entrambi blocchi di costruzione, o dipendenze di progetti creativi e software. La realtà è che un mattoncino Lego e il caso della backdoor XZ hanno molto di più di tutto ciò in comune.
Partecipate alla presentazione per immergervi in una storia di interoperabilità, standard e formati aperti, per poi discutere del ruolo importante che i contributori hanno in una comunità open source sostenibile.
BIO: Sostenitrice del software libero e dei formati standard e aperti. È stata un membro attivo dei progetti Fedora e openSUSE e ha co-fondato l'Associazione LibreItalia dove è stata coinvolta in diversi eventi, migrazioni e formazione relativi a LibreOffice. In precedenza ha lavorato a migrazioni e corsi di formazione su LibreOffice per diverse amministrazioni pubbliche e privati. Da gennaio 2020 lavora in SUSE come Software Release Engineer per Uyuni e SUSE Manager e quando non segue la sua passione per i computer e per Geeko coltiva la sua curiosità per l'astronomia (da cui deriva il suo nickname deneb_alpha).
Let's Integrate MuleSoft RPA, COMPOSER, APM with AWS IDP along with Slack
Discover the seamless integration of RPA (Robotic Process Automation), COMPOSER, and APM with AWS IDP enhanced with Slack notifications. Explore how these technologies converge to streamline workflows, optimize performance, and ensure secure access, all while leveraging the power of AWS IDP and real-time communication via Slack notifications.
Encryption in Microsoft 365 - ExpertsLive Netherlands 2024
In this session I delve into the encryption technology used in Microsoft 365 and Microsoft Purview. Including the concepts of Customer Key and Double Key Encryption.
Removing Uninteresting Bytes in Software Fuzzing
Imagine a world where software fuzzing, the process of mutating bytes in test seeds to uncover hidden and erroneous program behaviors, becomes faster and more effective. A lot depends on the initial seeds, which can significantly dictate the trajectory of a fuzzing campaign, particularly in terms of how long it takes to uncover interesting behaviour in your code. We introduce DIAR, a technique designed to speedup fuzzing campaigns by pinpointing and eliminating those uninteresting bytes in the seeds. Picture this: instead of wasting valuable resources on meaningless mutations in large, bloated seeds, DIAR removes the unnecessary bytes, streamlining the entire process.
In this work, we equipped AFL, a popular fuzzer, with DIAR and examined two critical Linux libraries -- Libxml's xmllint, a tool for parsing xml documents, and Binutil's readelf, an essential debugging and security analysis command-line tool used to display detailed information about ELF (Executable and Linkable Format). Our preliminary results show that AFL+DIAR does not only discover new paths more quickly but also achieves higher coverage overall. This work thus showcases how starting with lean and optimized seeds can lead to faster, more comprehensive fuzzing campaigns -- and DIAR helps you find such seeds.
- These are slides of the talk given at IEEE International Conference on Software Testing Verification and Validation Workshop, ICSTW 2022.
Presentation of the OECD Artificial Intelligence Review of Germany
Consult the full report at https://www.oecd.org/digital/oecd-artificial-intelligence-review-of-germany-609808d6-en.htm
GraphSummit Singapore | Neo4j Product Vision & Roadmap - Q2 2024
Maruthi Prithivirajan, Head of ASEAN & IN Solution Architecture, Neo4j
Get an inside look at the latest Neo4j innovations that enable relationship-driven intelligence at scale. Learn more about the newest cloud integrations and product enhancements that make Neo4j an essential choice for developers building apps with interconnected data and generative AI.
Unlock the Future of Search with MongoDB Atlas_ Vector Search Unleashed.pdf
Discover how MongoDB Atlas and vector search technology can revolutionize your application's search capabilities. This comprehensive presentation covers:
* What is Vector Search?
* Importance and benefits of vector search
* Practical use cases across various industries
* Step-by-step implementation guide
* Live demos with code snippets
* Enhancing LLM capabilities with vector search
* Best practices and optimization strategies
Perfect for developers, AI enthusiasts, and tech leaders. Learn how to leverage MongoDB Atlas to deliver highly relevant, context-aware search results, transforming your data retrieval process. Stay ahead in tech innovation and maximize the potential of your applications.
#MongoDB #VectorSearch #AI #SemanticSearch #TechInnovation #DataScience #LLM #MachineLearning #SearchTechnology
Essentials of Automations: The Art of Triggers and Actions in FME
In this second installment of our Essentials of Automations webinar series, we’ll explore the landscape of triggers and actions, guiding you through the nuances of authoring and adapting workspaces for seamless automations. Gain an understanding of the full spectrum of triggers and actions available in FME, empowering you to enhance your workspaces for efficient automation.
We’ll kick things off by showcasing the most commonly used event-based triggers, introducing you to various automation workflows like manual triggers, schedules, directory watchers, and more. Plus, see how these elements play out in real scenarios.
Whether you’re tweaking your current setup or building from the ground up, this session will arm you with the tools and insights needed to transform your FME usage into a powerhouse of productivity. Join us to discover effective strategies that simplify complex processes, enhancing your productivity and transforming your data management practices with FME. Let’s turn complexity into clarity and make your workspaces work wonders!
UiPath Test Automation using UiPath Test Suite series, part 6
Welcome to UiPath Test Automation using UiPath Test Suite series part 6. In this session, we will cover Test Automation with generative AI and Open AI.
UiPath Test Automation with generative AI and Open AI webinar offers an in-depth exploration of leveraging cutting-edge technologies for test automation within the UiPath platform. Attendees will delve into the integration of generative AI, a test automation solution, with Open AI advanced natural language processing capabilities.
Throughout the session, participants will discover how this synergy empowers testers to automate repetitive tasks, enhance testing accuracy, and expedite the software testing life cycle. Topics covered include the seamless integration process, practical use cases, and the benefits of harnessing AI-driven automation for UiPath testing initiatives. By attending this webinar, testers, and automation professionals can gain valuable insights into harnessing the power of AI to optimize their test automation workflows within the UiPath ecosystem, ultimately driving efficiency and quality in software development processes.
What will you get from this session?
1. Insights into integrating generative AI.
2. Understanding how this integration enhances test automation within the UiPath platform
3. Practical demonstrations
4. Exploration of real-world use cases illustrating the benefits of AI-driven test automation for UiPath
Topics covered:
What is generative AI
Test Automation with generative AI and Open AI.
UiPath integration with generative AI
Speaker:
Deepak Rai, Automation Practice Lead, Boundaryless Group and UiPath MVP
Video Streaming: Then, Now, and in the Future
In his public lecture, Christian Timmerer provides insights into the fascinating history of video streaming, starting from its humble beginnings before YouTube to the groundbreaking technologies that now dominate platforms like Netflix and ORF ON. Timmerer also presents provocative contributions of his own that have significantly influenced the industry. He concludes by looking at future challenges and invites the audience to join in a discussion.
Recently uploaded (20)
National Security Agency - NSA mobile device best practices
National Security Agency - NSA mobile device best practices
Communications Mining Series - Zero to Hero - Session 1
Communications Mining Series - Zero to Hero - Session 1
20240609 QFM020 Irresponsible AI Reading List May 2024
20240609 QFM020 Irresponsible AI Reading List May 2024
Pushing the limits of ePRTC: 100ns holdover for 100 days
Pushing the limits of ePRTC: 100ns holdover for 100 days
Enchancing adoption of Open Source Libraries. A case study on Albumentations.AI
Enchancing adoption of Open Source Libraries. A case study on Albumentations.AI
A tale of scale & speed: How the US Navy is enabling software delivery from l...
A tale of scale & speed: How the US Navy is enabling software delivery from l...
Cosa hanno in comune un mattoncino Lego e la backdoor XZ?
Cosa hanno in comune un mattoncino Lego e la backdoor XZ?
Let's Integrate MuleSoft RPA, COMPOSER, APM with AWS IDP along with Slack
Let's Integrate MuleSoft RPA, COMPOSER, APM with AWS IDP along with Slack
Encryption in Microsoft 365 - ExpertsLive Netherlands 2024
Encryption in Microsoft 365 - ExpertsLive Netherlands 2024
Presentation of the OECD Artificial Intelligence Review of Germany
Presentation of the OECD Artificial Intelligence Review of Germany
GraphSummit Singapore | Neo4j Product Vision & Roadmap - Q2 2024
GraphSummit Singapore | Neo4j Product Vision & Roadmap - Q2 2024
Unlock the Future of Search with MongoDB Atlas_ Vector Search Unleashed.pdf
Unlock the Future of Search with MongoDB Atlas_ Vector Search Unleashed.pdf
Essentials of Automations: The Art of Triggers and Actions in FME
Essentials of Automations: The Art of Triggers and Actions in FME
UiPath Test Automation using UiPath Test Suite series, part 6
UiPath Test Automation using UiPath Test Suite series, part 6
4.10.08 Graphs Of Polynomials
- 2. Let’s look at a graph. Use your calculator to graph the following, and sketch a copy in your notes for reference: The graph should look something like this:
- 4. Zeros A function has a value of zero at its x -intercept(s). How many zeros does our function have? Can you use your calculator to find them?
- 5. Increasing/decreasing Intervals Polynomial functions tend to zig-zag around a bit. If you imagine you are driving a car from left to right along the graph, the graph is increasing if you are driving uphill, and decreasing if you are driving downhill. Where is our function increasing? Decreasing? How are the concepts of increasing and decreasing related to slope?
- 6. Positive/negative Intervals Positive and negative intervals refer to the value of the function, which means the y -value. Where is our function positive? Negative?