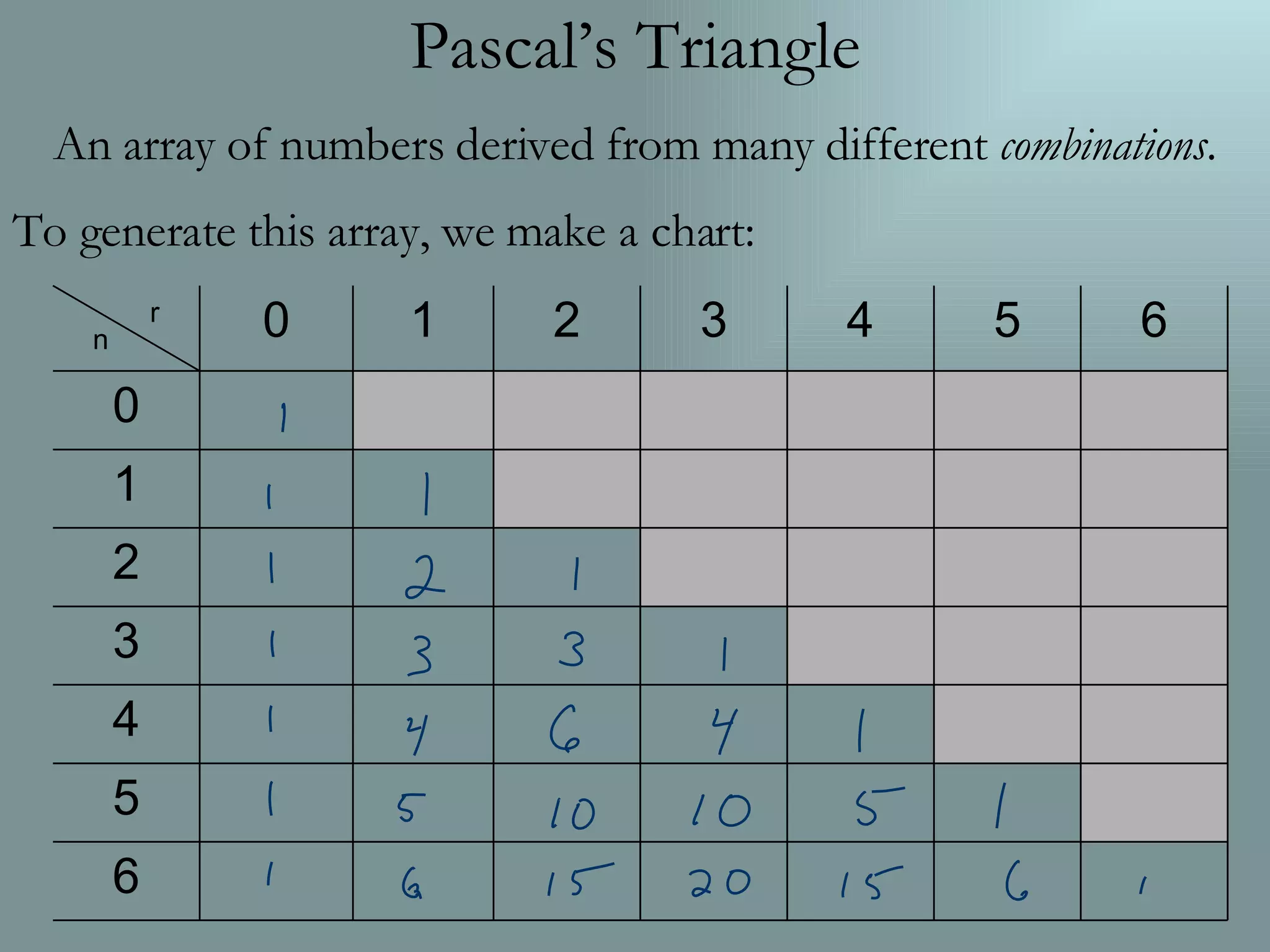
Pascal's Triangle is an array of numbers arranged in triangular form where each number is derived from adding the two numbers directly above it. To generate the triangle, a chart is made where the terms are found by taking the binomial coefficients of n over r, and properties include that each row has one more term than the previous row and the first and last terms of each row are always 1.

1. Pascal’s Triangle An array of numbers derived from many different combinations . To generate this array, we make a chart: 6 5 4 3 2 1 0 6 5 4 3 2 1 0 n r

2. Pascal’s Triangle An array of numbers derived from many different combinations . To generate this array, we make a chart: 6 5 4 3 2 1 0 6 5 4 3 2 1 0 n r

3. Pascal’s Triangle We more commonly see the triangle written in its isosceles form: To find the r th term of the n th row, what would you do? . In other words, gives you the (r +1) st term in the n th row.

4. Some Properties of Pascal’s Triangle 1. 2. 3. 4. 5.

5. Find the first four terms in row 9 of Pascal’s Triangle. Find the last four terms in row 9 of Pascal’s Triangle. Find the remaining two terms in row 9 of Pascal’s Triangle.