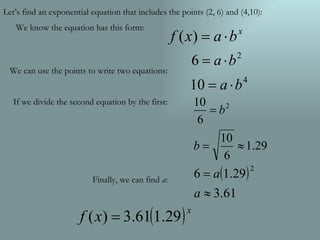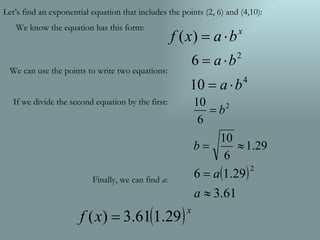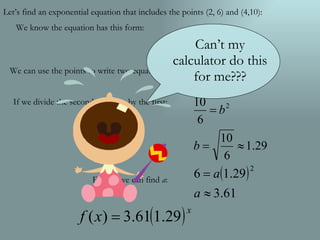The document compares exponential and linear models. Exponential models exhibit constant percentage change determined by the growth factor b, while linear models show constant increase/decrease set by the slope m. Exponential equations can be determined from a single point, unlike linear equations which require two points to find the parameters m and b. The document demonstrates finding the exponential equation for two given points (2,6) and (4,10) by setting up equations and dividing them to isolate the growth factor b.

1. Exponential Models Recall that an exponential function is of the form f ( x ) = ab x , where a ≠ 0, b >0, and b ≠ 1. When using an exponential function as a model for a real-life situation, x often represents time. Since f (0)= a , a is referred to as the initial value of the dependent variable. b , on the other hand, is known as the growth factor . Initial Value Growth Factor

2. How do exponential models compare with linear models? The parameter that controls the “growth” of each type of functions works differently in each case. A linear model exhibits constant increase/decrease , which is determined by m . An exponential model exhibits constant percentage change , which is determined by b . Rate of increase/decrease Growth factor (% change)

3. How do exponential models compare with linear models? To find an equation of a line, we need two points. This is related to the fact that there are two parameters in the equation: m and b . How many points do you think we need to determine an exponential equation?

4. We can use the points to write two equations: If we divide the second equation by the first: Finally, we can find a : Let’s find an exponential equation that includes the points (2, 6) and (4,10): We know the equation has this form:

5. We can use the points to write two equations: If we divide the second equation by the first: Finally, we can find a : Let’s find an exponential equation that includes the points (2, 6) and (4,10): We know the equation has this form:

6. We can use the points to write two equations: If we divide the second equation by the first: Finally, we can find a : Let’s find an exponential equation that includes the points (2, 6) and (4,10): We know the equation has this form: Can’t my calculator do this for me???