The trapezoidal method splits the area under a curve into trapezoids, calculates the area of each trapezoid, and sums the individual areas to approximate the total area under the curve, which represents the definite integral. It uses the formula: Integral = (h/2) * (y0 + 2*y1 + 2*y2 + ... + 2*yn-1 + yn), where h is the width of each interval between the x-values x0, x1, etc., and y0, y1, etc. are the corresponding y-values of the function. Simpson's 1/3 Rule similarly divides the interval into sub-intervals, but approximates each using a quadratic curve

1. Trapizoidal Rule

2. The basic working principle of the trapezoidal method c program is that trapezoidal
method splits the area under the curve into a number of trapeziums. Then, area of
each trapezium is calculated, and all the individual areas are summed up to give the
total area under the curve which is the value of definite integral.
In the figure, area under the curve between the points x0
and xn is to be determined. In order to determine the area,
we divide the total interval (xn– x0) into ‘n’ small interval
each of length ‘h’:
h=(xn– x0)/n
After that, the C source code for trapezoidal method uses
the following formula to calculate the value of definite
integral:

3. Steps
• 1. take n that is number of intervals
• 2. calculate h=(b-a)/n , a is lower limit and b is upper limit
• 3. find x0=a, x1=a+h, x2=a+2.h , …..
• 4. using y=f(x), Find y0,y1,y2….
• 5.

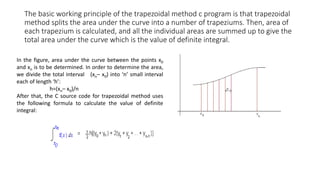
4. Example:
• ⌠1
4 (x2 +2X)dx with n=6
• ANSWER:
• n=6, h=(b-a)/n=3/6=0.5
•
• ⌠1
4 (x2 +2X)dx=h/2[(3+24)+ 2*(5.25+8+11.25+15+19.25)]=36.125
•
X 1 1.5 2 2.5 3 3.5 4
Y 3 5.25 8 11.25 15 19.25 24

5. Simpson’s 1/3rd Rule:
• Simpson’s Rule is a Numerical technique to find the definite
integral of a function within a given interval.
• The function is divided into many sub-intervals and each
interval is approximated by a quadratic curve. And the area is
then calculated to find the integral. The more is the number of
sub-intervals used, the better is the approximation.
•
NOTE: The no. of sub-intervals should be EVEN.

6. Integral = *((y0 + yn ) +4(y1 + y3 + ……….+ yn-1 )
+ 2(y2 + y4 +……….+ yn-2 ))