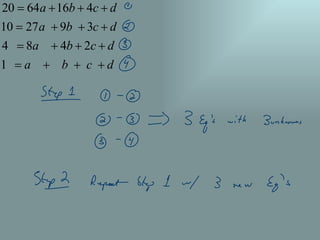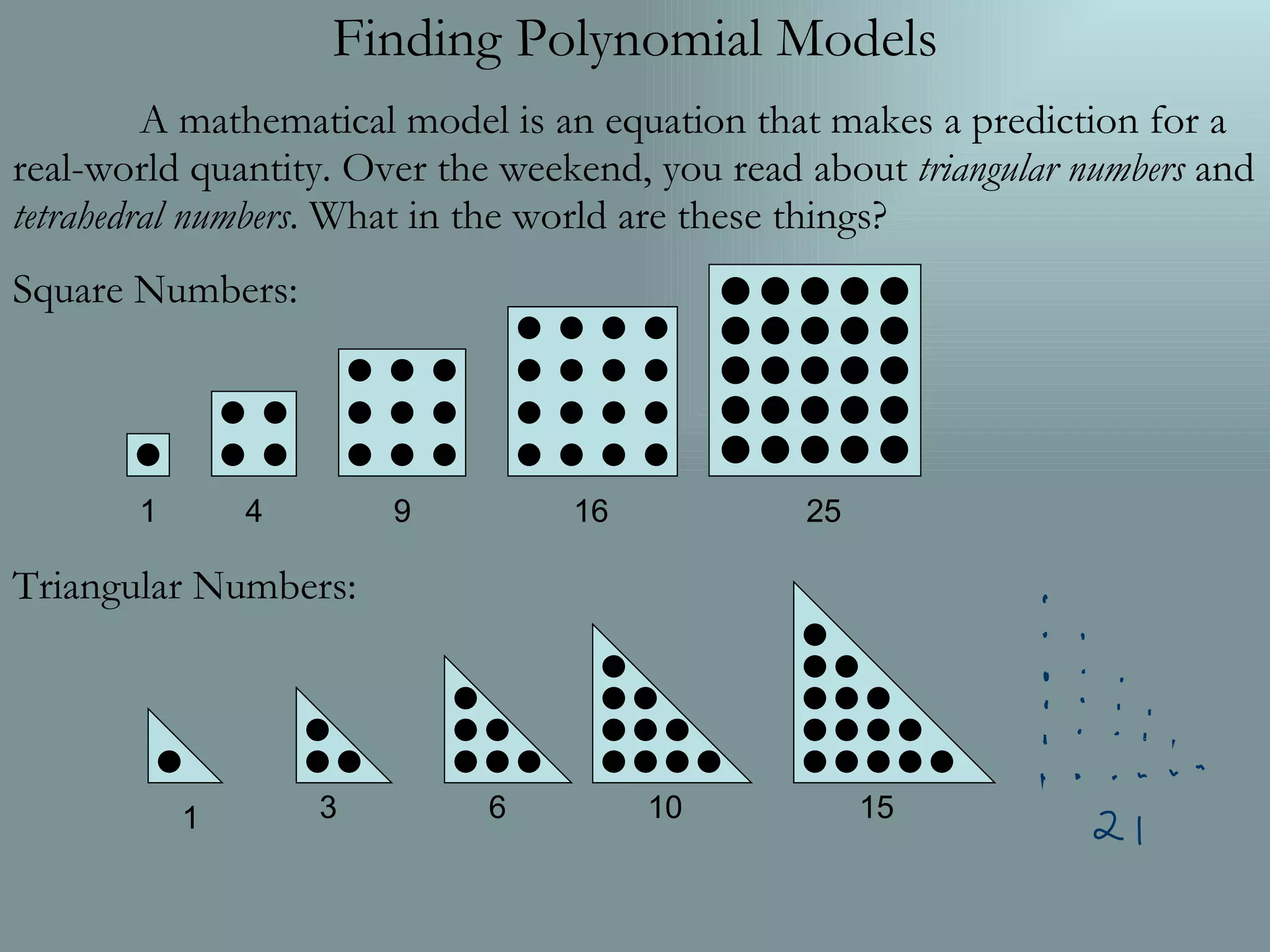
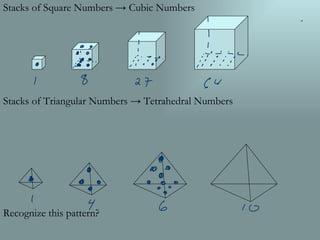
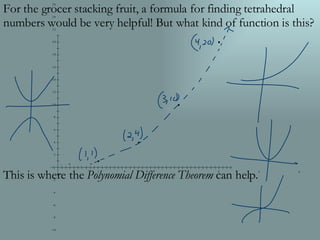
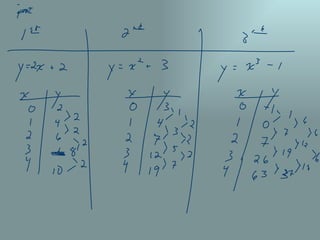
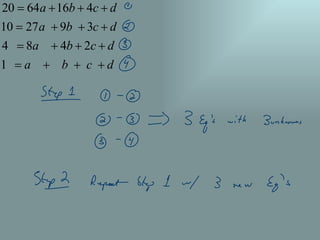
The document discusses finding polynomial models to describe patterns like triangular numbers and tetrahedral numbers. It explains that a polynomial difference theorem can be used to find the polynomial formula for functions where the differences between successive values form a known pattern. Specifically, if the fourth differences are constant, the function is a fourth degree polynomial that can be determined by plugging known points into the general cubic polynomial formula.

1. Finding Polynomial Models A mathematical model is an equation that makes a prediction for a real-world quantity. Over the weekend, you read about triangular numbers and tetrahedral numbers . What in the world are these things? Square Numbers: Triangular Numbers: 1 4 9 25 16 1 3 6 10 15

2. Stacks of Square Numbers -> Cubic Numbers Stacks of Triangular Numbers -> Tetrahedral Numbers Recognize this pattern?

3. For the grocer stacking fruit, a formula for finding tetrahedral numbers would be very helpful! But what kind of function is this? This is where the Polynomial Difference Theorem can help.

4. 4 th Differences 3 rd Differences 2 nd Differences 1 st Differences 56 35 20 10 4 1 f(x) 6 5 4 3 2 1 x

6. If we know our function is a cubic polynomial, then it must be of the form To find a, b, c, and d , we need four equations, which we can get by plugging in four of the points that we know satisfy the function:

9. There exists a polynomial formula of degree 4 for the sum of the cubes of the integers from 1 to n . Find that formula.