Embed presentation
Downloaded 155 times



Thomas Simpson published Simpson's Rule in 1743, which uses parabolas instead of straight lines to better approximate the area under a curve. Simpson's Rule requires an even number of intervals or ordinates and is more accurate than the Trapezium Rule. Two examples are provided where Simpson's Rule is used with either five ordinates or four intervals to estimate the value of integrals.






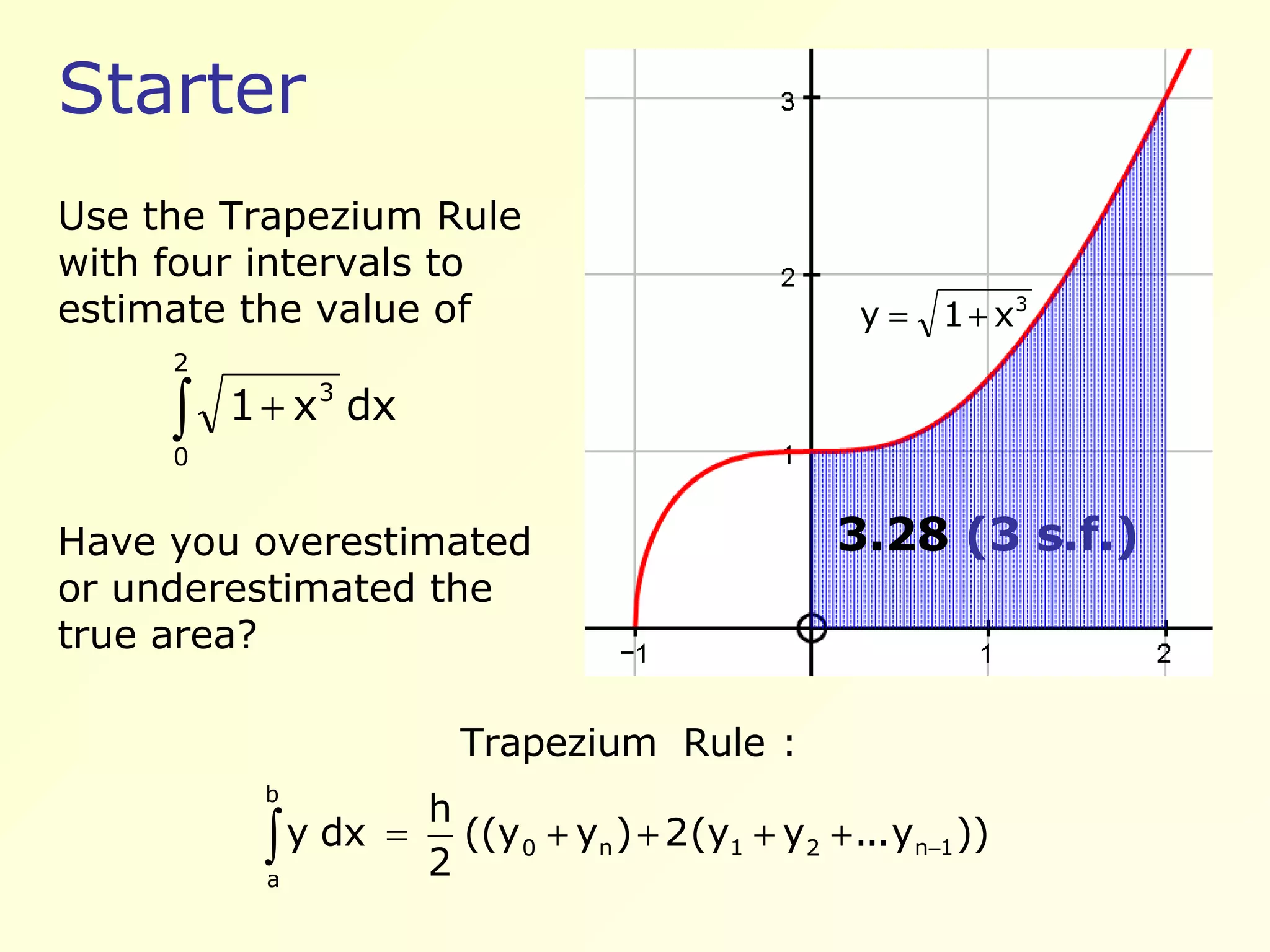
Estimate the area using the Trapezium Rule across four intervals; value approximately 3.28.
Objective to understand Simpson’s Rule, introduced by Thomas Simpson, who lived from 1710 to 1761.
Simpson’s Rule provides more accuracy than the Trapezium Rule by using parabolas; requires even intervals.
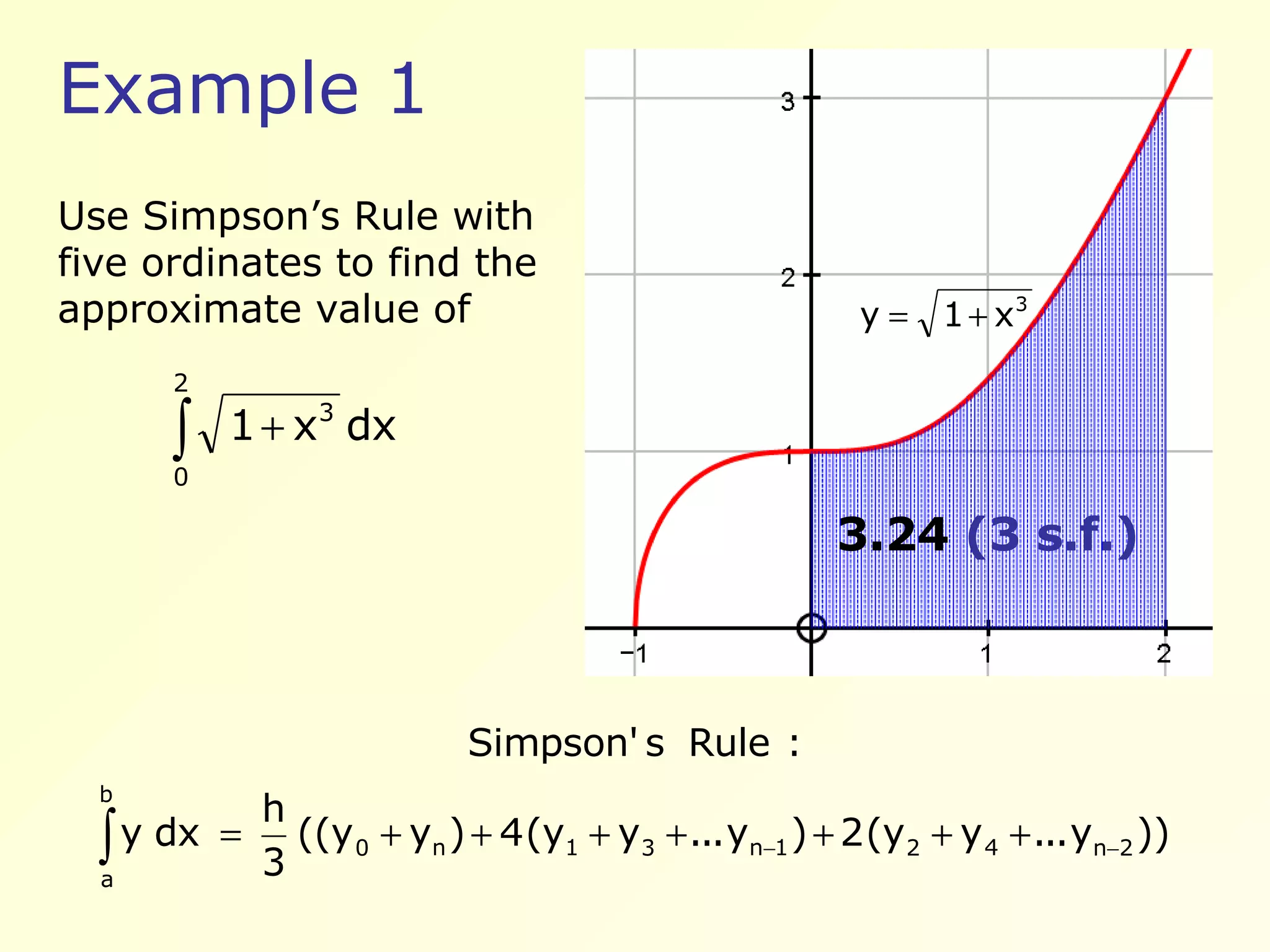
Example using Simpson's Rule with five ordinates results in an approximate value of 3.24.
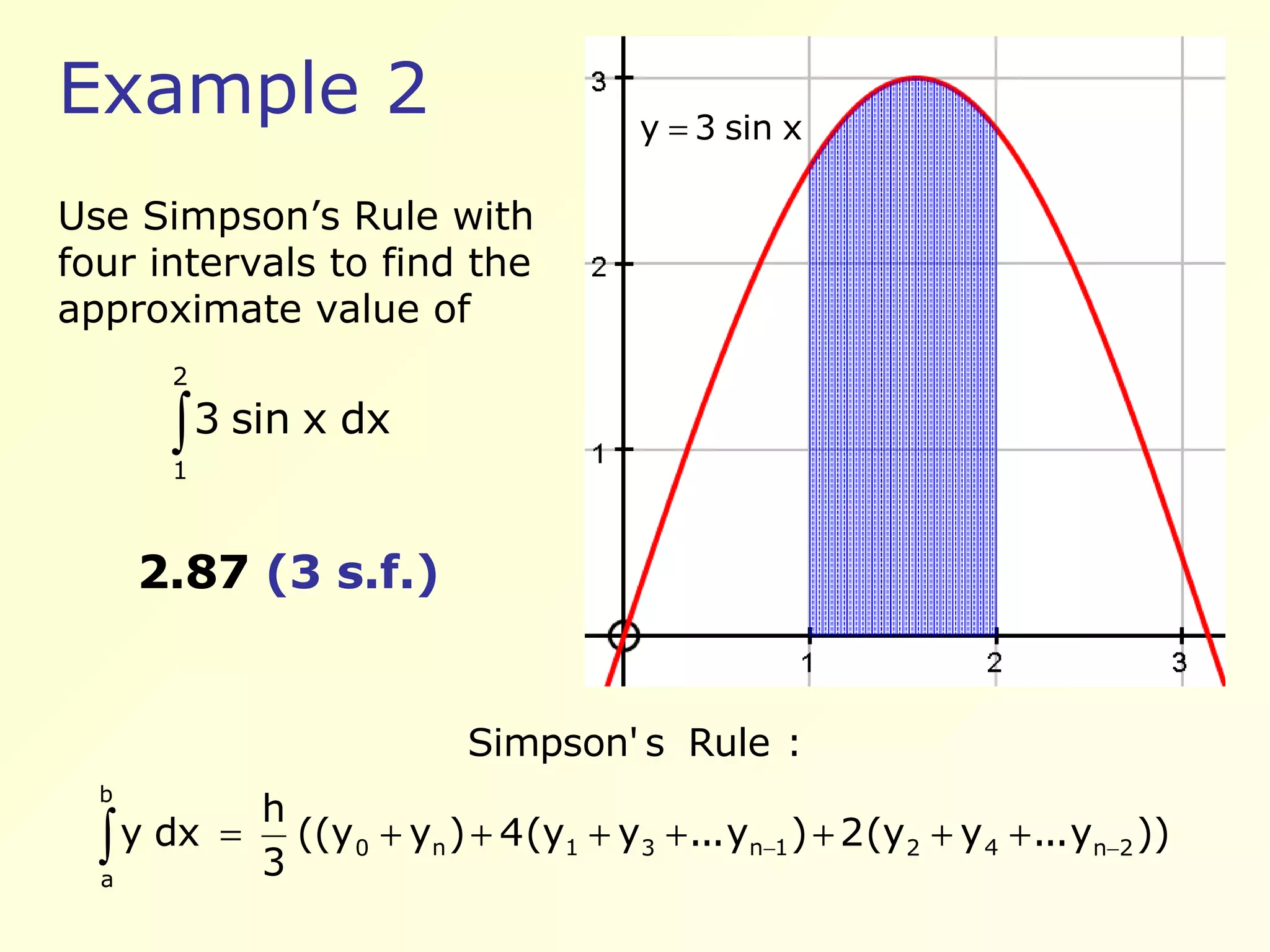
Second example using Simpson's Rule with four intervals yields an approximate value of 2.87.
Reference to Core 3 & 4, Textbook Exercise 12B on Page 188 for further exercises.