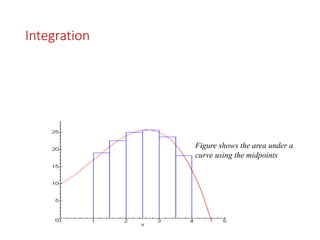
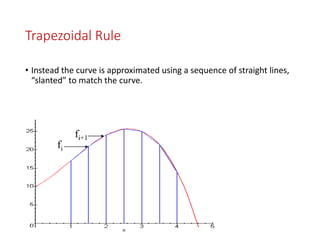
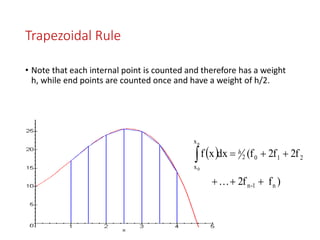
This document discusses numerical integration and its applications. It introduces various numerical integration methods like the trapezoidal rule and Simpson's rule. The trapezoidal rule approximates the curve using straight lines between points to calculate the area under the curve. Simpson's rule further improves upon this by approximating the curve with a quadratic or cubic function between points. The document explains the formulas for the trapezoidal rule, Simpson's 1/3 rule, and Simpson's 3/8 rule.

1. Topic : Numerical Integration & its Application.
Subject: Numerical & Statistical Methods
Name: Hemali Bishnoi (150953131003)
Dhvani Pandya (150953131011)
Shivani Saini (150953131020)
Batch : A3

2. Integration is an important in Physics.
Used to determine the rate of growth in bacteria or to
find the distance given the velocity (s = ∫vdt) as well as
many other uses.
The most familiar practical (probably the 1
st
usage)
use of integration is to calculate the area.
Integration

3. Integration
• Generally we use formulae to determine the integral of a function:
• F(x) can be found if its antiderivative, f(x) is known.
     aFbFdxxf
b
a


4. Integration
• when the antiderivative is unknown we are required to determine
f(x) numerically.
• To determine the definite integral we find the area between the
curve and the x-axis.
• This is the principle of numerical integration.

5. Integration
Figure shows the area under a
curve using the midpoints

6. Integration
• There are various integration methods: Trapezoid, Simpson’s, etc.
• We’ll be looking in detail at the Trapezoid and variants of the
Simpson’s method.

7. Trapezoidal Rule
• is an improvement on the midpoint implementation.
• the midpoints is inaccurate in that there are pieces of the “boxes”
above and below the curve (over and under estimates).

8. Trapezoidal Rule
• Instead the curve is approximated using a sequence of straight lines,
“slanted” to match the curve.
fi
fi+1

9. Trapezoidal Rule
• Clearly the area of one rectangular strip from xi to xi+1 is given by
• Generally is used. h is the width of a strip.
  iiii xxff   11I
)x-(x½h i1i
1...

10. Trapezoidal Rule
• The composite Trapezium rule is obtained by applying the equation
.1 over all the intervals of interest.
• Thus,
,if the interval h is the same for each strip.
 n1-n2102 f2f2f2ffI  h

11. Trapezoidal Rule
• Note that each internal point is counted and therefore has a weight
h, while end points are counted once and have a weight of h/2.
 
)f2f
2f2f(fdxxf
n1-n
2102
x
x
n
0

 h

12. Simpson’s Rule
• The midpoint rule was first improved upon by the trapezium rule.
• A further improvement is the Simpson's rule.
• Instead of approximating the curve by a straight line, we approximate
it by a quadratic or cubic function.

13. Simpson’s Rule
•Diagram showing approximation using Simpson’s
Rule.

14. Simpson’s Rule
• There are two variations of the rule: Simpson’s 1/3 rule
and Simpson’s 3/8 rule.
• The formula for the Simpson’s 1/3,
   n1-n32103
x
x
f4f4f2f4ffdxxf
n
0
 h

15. Simpson’s Rule
• The integration is over pairs of intervals and requires that total
number of intervals be even of the total number of points N be odd.

16. Simpson’s Rule
• The formula for the Simpson’s 3/8,
   n1-n32108
3
x
x
f3f2f3f3ffdxxf
n
0
 h
If the number of strips is divisible by three we can use
the 3/8 rule.

17. Thank You