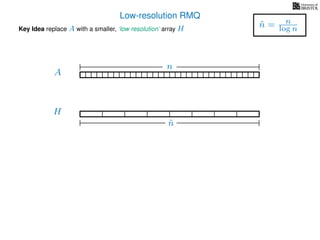
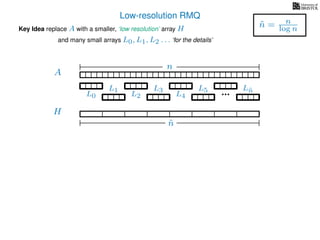
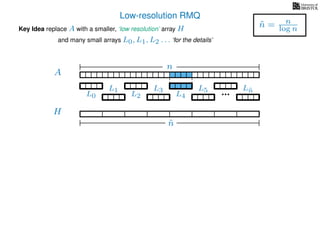
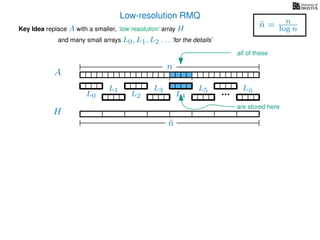
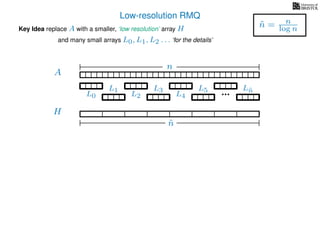
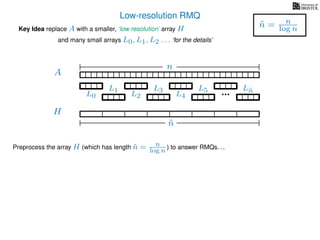
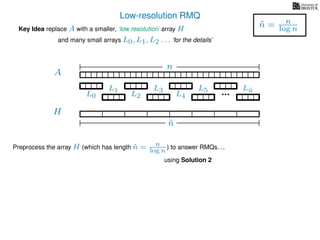
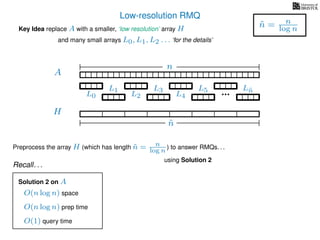
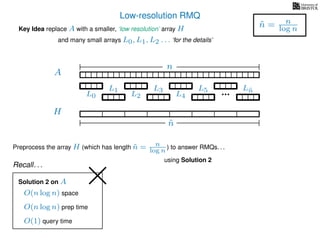
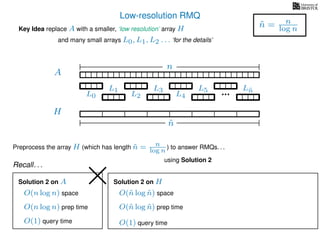
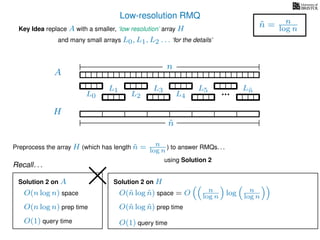
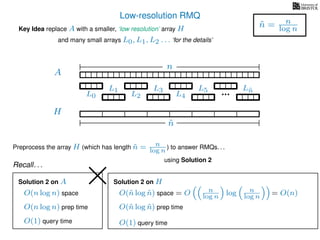
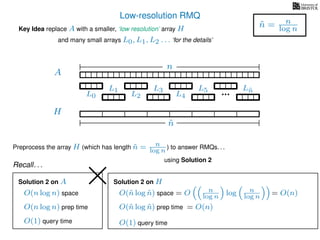
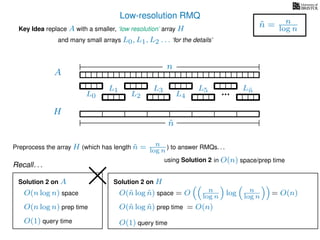
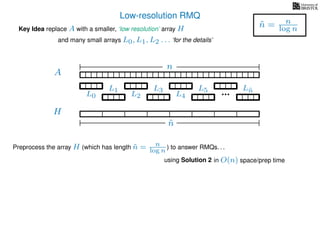
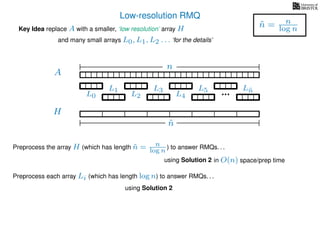
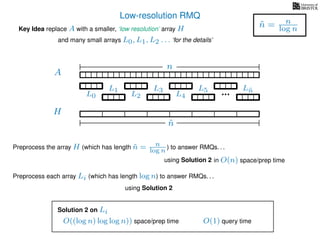
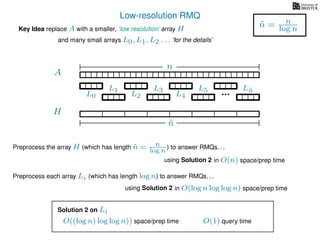
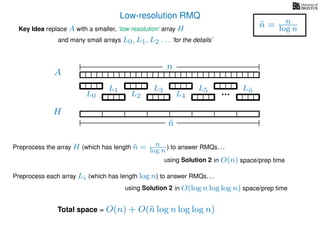
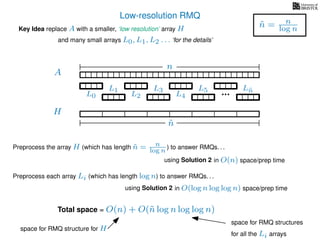
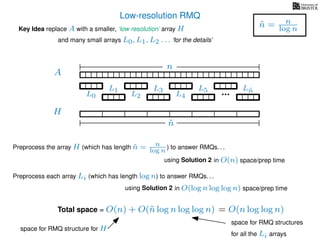
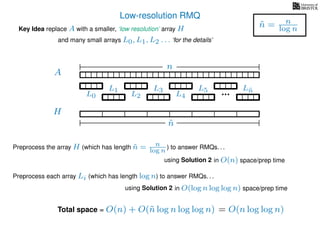
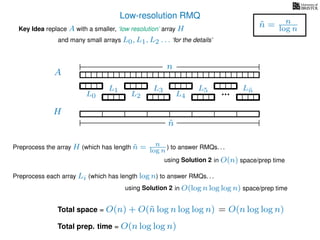
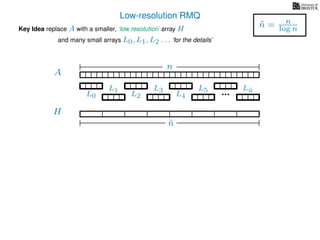
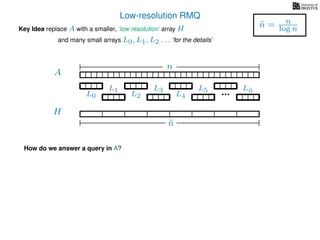
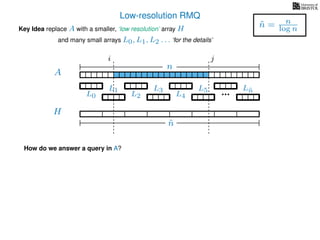
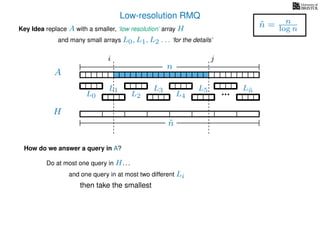
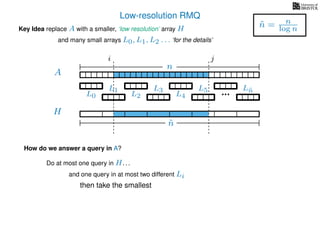
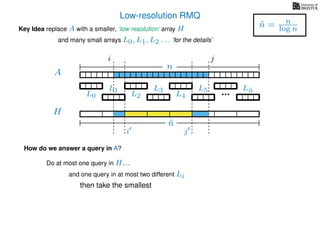
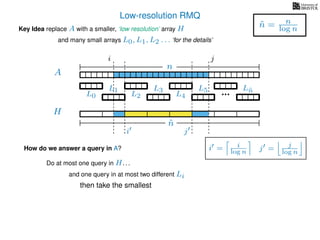
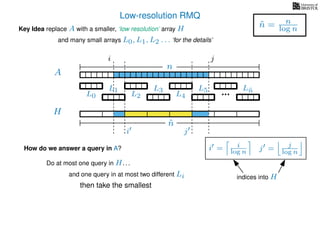
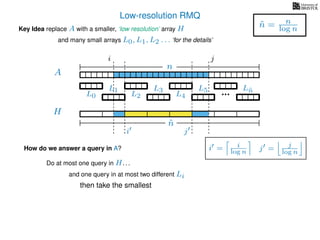
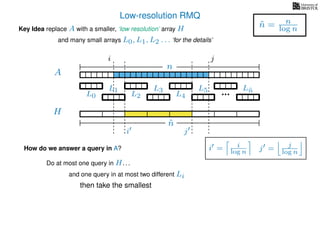
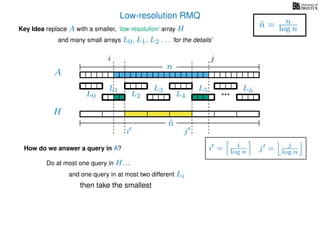
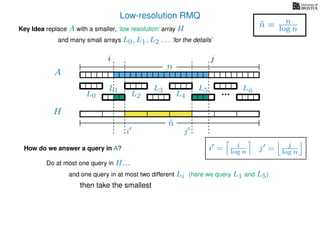
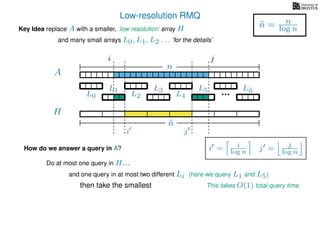
The document discusses algorithms for preprocessing an integer array to efficiently answer range minimum queries (RMQ). It includes methods for determining the location of the smallest element within a specified range after preprocessing and outlines trade-offs involving space, preparation time, and query time. Various techniques such as block decomposition and the use of auxiliary arrays to store minimum values for different blocks are introduced to optimize RMQ performance.

1. Advanced Algorithms – COMS31900
Range Minimum Queries
Benjamin Sach

2. Range minimum query
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

3. Range minimum query
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

4. Range minimum query
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

5. Range minimum query
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

6. Range minimum query
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
19 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

7. Range minimum query
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
RMQ(3, 7) = 6
19 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

8. Range minimum query
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
e.g. RMQ(3, 7) = 6, which is the location of the smallest element in A[3, 7]
i = 3 j = 7
RMQ(3, 7) = 6
19 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

9. Range minimum query
i = 5 j = 11
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
e.g. RMQ(3, 7) = 6, which is the location of the smallest element in A[3, 7]
RMQ(5, 11) = 8
e.g. RMQ(5, 11) = 8, which is the location of the smallest element in A[5, 11]
9 21 545
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

10. Range minimum query
i = 5 j = 11
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
e.g. RMQ(3, 7) = 6, which is the location of the smallest element in A[3, 7]
RMQ(5, 11) = 8
e.g. RMQ(5, 11) = 8, which is the location of the smallest element in A[5, 11]
• We will discuss several algorithms which give trade-offs between
space used, prep. time and query time
9 21 545
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

11. Range minimum query
i = 5 j = 11
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
e.g. RMQ(3, 7) = 6, which is the location of the smallest element in A[3, 7]
RMQ(5, 11) = 8
e.g. RMQ(5, 11) = 8, which is the location of the smallest element in A[5, 11]
• We will discuss several algorithms which give trade-offs between
space used, prep. time and query time
• Ideally we would like O(n) space, O(n) prep. time and O(1) query time
9 21 545
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

12. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
19

13. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
19

14. Block decomposition
smallest from each pair
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
19

15. Block decomposition
smallest from each pair
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
19

16. Block decomposition
smallest from each pair
19A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
19

17. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
19

18. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
19

19. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
smallest from each four
1919

20. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
smallest from each four
1919

21. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
19

22. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
19

23. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
smallest from each eight
19

24. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
smallest from each eight
8 19

25. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
19

26. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
19

27. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
19

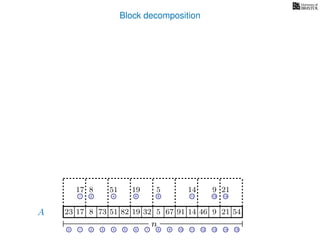
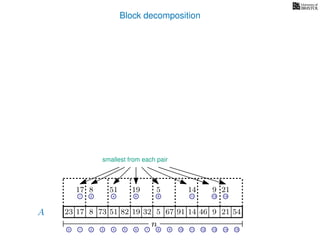
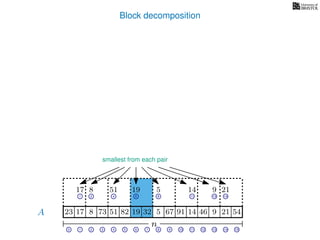
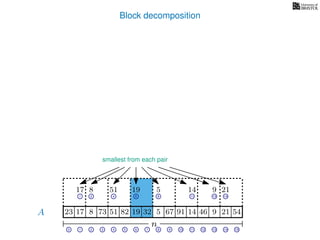
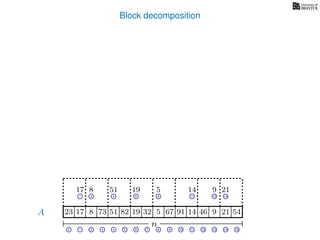
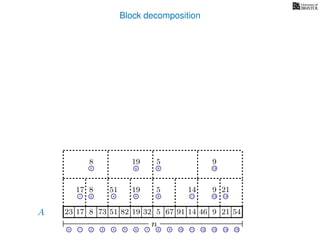
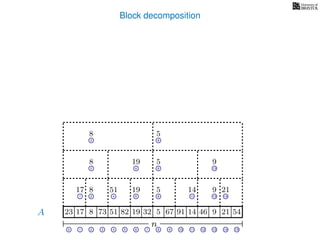
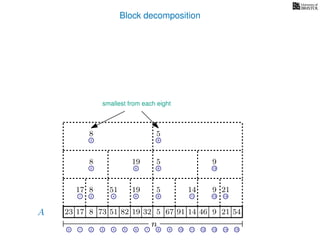
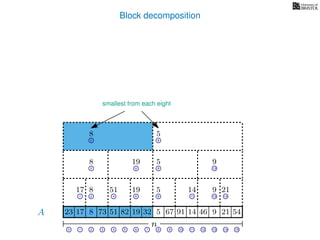
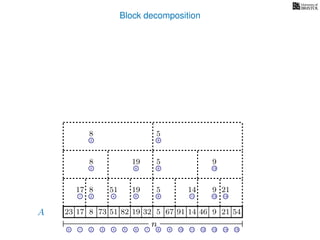
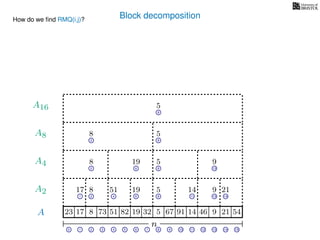
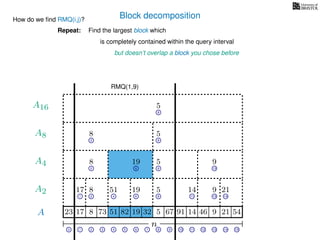
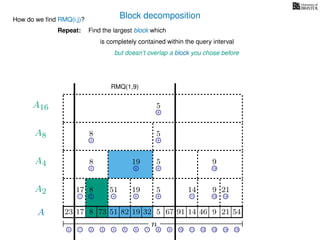
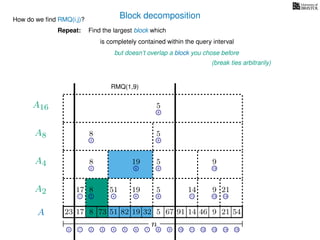
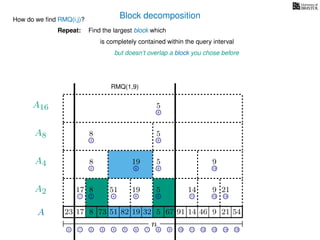
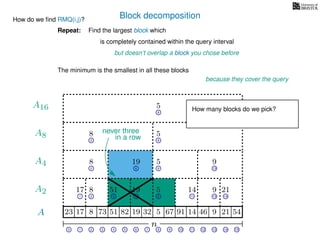
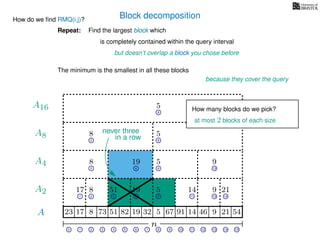
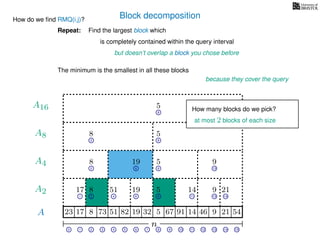
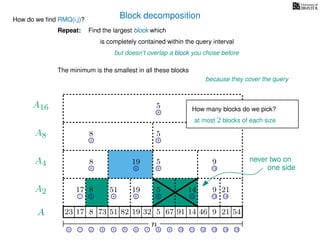
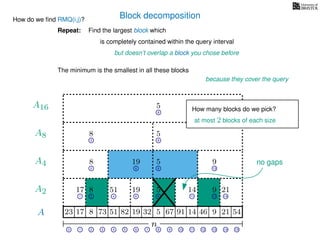
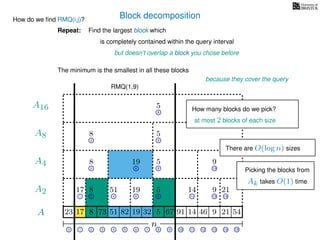
28. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
19

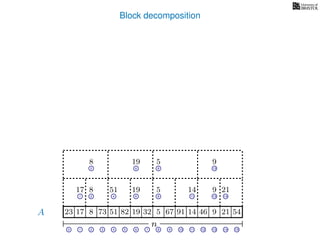
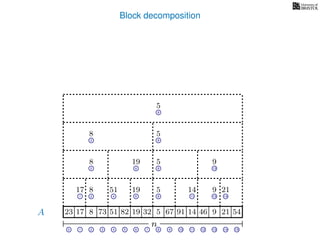
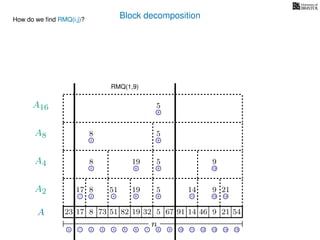
29. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
19

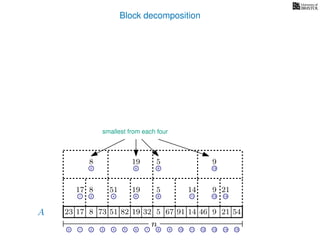
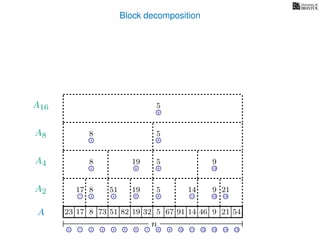
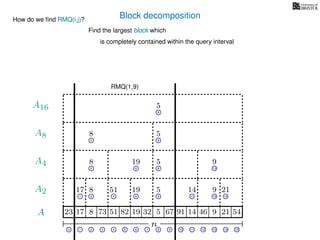
30. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
How much space is this?
19

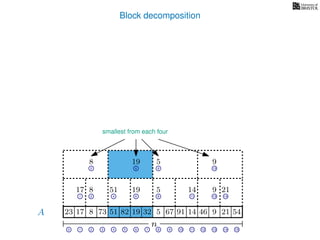
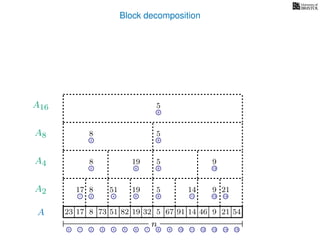
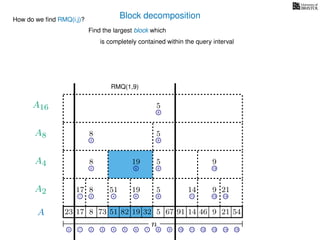
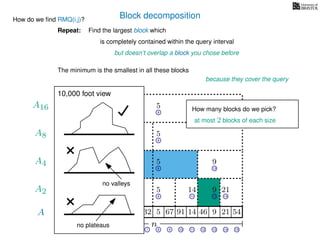
31. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
How much space is this? O(n) in total
19

32. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
How much space is this? O(n) in total
n
2
n
4
n
8
n
16
+
+
+
+
19

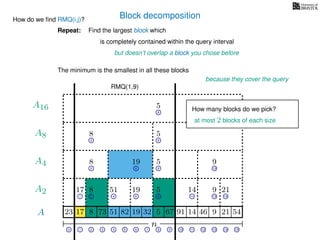
33. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
How much space is this? O(n) in total
n
2
n
4
n
8
n
16
+
+
+
+
O(n)
19

34. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
How much space is this? O(n) in total
19

35. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
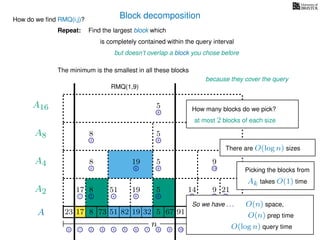
How much space is this? O(n) in total
How quickly can we build them?
19

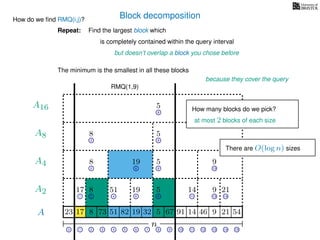
36. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
How much space is this? O(n) in total
How quickly can we build them?
construct the Ak
arrays bottom-up
19

37. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
How much space is this? O(n) in total
How quickly can we build them?
compute this from
these in O(1) time
construct the Ak
arrays bottom-up
19

38. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
How much space is this? O(n) in total
How quickly can we build them? O(n) preprocessing time
compute this from
these in O(1) time
construct the Ak
arrays bottom-up
19

39. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
Ak is an array of length n
k so that for all i: Ak[i] = (x, v)
where v is the minimum in A[ik, (i + 1)k] and x is its location in A.
We store Ak for all k = 1, 2, 4, 8 . . . n
How much space is this? O(n) in total
How quickly can we build them? O(n) preprocessing time
19

40. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
19

41. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
19

42. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
RMQ(1,9)
19

43. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
RMQ(1,9)
19

44. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
RMQ(1,9)
19

45. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
RMQ(1,9)
Repeat:
19

46. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
RMQ(1,9)
Repeat:
19

47. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
RMQ(1,9)
Repeat:
(break ties arbitrarily)
19

48. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
RMQ(1,9)
Repeat:
19

49. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
RMQ(1,9)
Repeat:
19

50. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
RMQ(1,9)
Repeat:
19

51. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
RMQ(1,9)
Repeat:
How many blocks do we pick?
19

52. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
19

53. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
19

54. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
19

55. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
19

56. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
19
never three
in a row

57. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
19
never three
in a row

58. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
19
never three
in a row

59. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
19

60. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
19
never two on
one side

61. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
19
never two on
one side

62. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
19

63. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
19

64. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
19
no gaps

65. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
19
no gaps

66. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
19
10,000 foot view
no valleys
no plateaus

67. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
RMQ(1,9)
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
19

68. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
RMQ(1,9)
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
There are O(log n) sizes
19

69. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
RMQ(1,9)
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
There are O(log n) sizes
Picking the blocks from
Ak takes O(1) time
19

70. Block decomposition
A
n
17 823 73 51 82 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
21 4 6 8 11 13 14
17 8 51 19 5 14 9 21
2 6 8 13
8 19 5 9
2 8
8 5
8
5
A2
A4
A8
A16
How do we find RMQ(i,j)?
Find the largest block which
is completely contained within the query interval
but doesn’t overlap a block you chose before
The minimum is the smallest in all these blocks
because they cover the query
RMQ(1,9)
Repeat:
How many blocks do we pick?
at most 2 blocks of each size
There are O(log n) sizes
Picking the blocks from
Ak takes O(1) time
So we have . . . O(n) space,
O(n) prep time
O(log n) query time
19

71. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A

72. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A

73. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
2
The array R2 stores RMQ(i, i + 1) for all i
A

74. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2

75. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2

76. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2

77. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2

78. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2

79. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2

80. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2

81. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2

82. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2

83. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2

84. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
2
stored in R2

85. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
R4 stores RMQ(i, i + 3) for all i
2
stored in R2

86. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
R4 stores RMQ(i, i + 3) for all i
2
stored in R2
4
stored in R4

87. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
2
stored in R2
4
stored in R4

88. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
2
stored in R2
4
stored in R4
8
stored in R8

89. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
2
stored in R2
4
stored in R4
8
stored in R8

90. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
2
stored in R2
4
stored in R4
8
stored in R8

91. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
2
stored in R2
4
stored in R4
8
stored in R8

92. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
2
stored in R2
4
stored in R4
8
stored in R8

93. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
2
stored in R2
4
stored in R4
8
stored in R8
We build R2 from A in O(n) time

94. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
2
stored in R2
4
stored in R4
8
stored in R8
We build R2 from A in O(n) time
We build R2k from Rk in O(n) time

95. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
2
stored in R2
4
stored in R4
8
stored in R8
We build R2 from A in O(n) time
We build R2k from Rk in O(n) time
how?

96. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
We build R2 from A in O(n) time
We build R2k from Rk in O(n) time
how?

97. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
We build R2 from A in O(n) time
We build R2k from Rk in O(n) time
how?
2k
k k

98. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
We build R2 from A in O(n) time
We build R2k from Rk in O(n) time
how?
2k
k k
the min in here

99. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
We build R2 from A in O(n) time
We build R2k from Rk in O(n) time
how?
2k
k k
the min in here
is the min of these two mins
(which we have in Rk)

100. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
We build R2 from A in O(n) time
We build R2k from Rk in O(n) time
how?

101. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
2
stored in R2
4
stored in R4
8
stored in R8
We build R2 from A in O(n) time
We build R2k from Rk in O(n) time
how?

102. More space, faster queries
Key Idea precompute the answers for every interval of length 2, 4, 8, 16 . . .
The array R2 stores RMQ(i, i + 1) for all i
A
We build Rk for k = 2, 4, 8, 16 . . . n
R4 stores RMQ(i, i + 3) for all i
R8 stores RMQ(i, i + 7) for all i
Rk stores RMQ(i, i + k − 1) for all i
each of the O(log n) arrays uses O(n) space
so O(n log n) total space
2
stored in R2
4
stored in R4
8
stored in R8
We build R2 from A in O(n) time
We build R2k from Rk in O(n) time
how?
This takes O(n log n) prep time

103. More space, faster queries
A
2
stored in R2
4
stored in R4
8
stored in R8
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer

104. More space, faster queries
A
2
stored in R2
4
stored in R4
8
stored in R8
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
8
stored in R8

105. More space, faster queries
A
2
stored in R2
4
stored in R4
8
stored in R8
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
8
stored in R8

106. More space, faster queries
A
2
stored in R2
4
stored in R4
8
stored in R8
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k

107. More space, faster queries
A
2
stored in R2
4
stored in R4
8
stored in R8
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k

108. More space, faster queries
A
2
stored in R2
4
stored in R4
8
stored in R8
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k
Compute the minimum of RMQ(i, i + k − 1) and RMQ(j − k + 1, j)

109. More space, faster queries
A
2
stored in R2
4
stored in R4
8
stored in R8
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k
Compute the minimum of RMQ(i, i + k − 1) and RMQ(j − k + 1, j)
(these two queries take O(1) time)

110. More space, faster queries
A
2
stored in R2
4
stored in R4
8
stored in R8
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k
Compute the minimum of RMQ(i, i + k − 1) and RMQ(j − k + 1, j)
(these two queries take O(1) time)

111. More space, faster queries
A
2
stored in R2
4
stored in R4
8
stored in R8
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k
Compute the minimum of RMQ(i, i + k − 1) and RMQ(j − k + 1, j)
(these two queries take O(1) time)
This takes O(1) time but why does it work?

112. More space, faster queries
A
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k
Compute the minimum of RMQ(i, i + k − 1) and RMQ(j − k + 1, j)
(these two queries take O(1) time)
This takes O(1) time but why does it work?

113. More space, faster queries
A
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k
Compute the minimum of RMQ(i, i + k − 1) and RMQ(j − k + 1, j)
(these two queries take O(1) time)
This takes O(1) time but why does it work?
i j

114. More space, faster queries
A
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k
Compute the minimum of RMQ(i, i + k − 1) and RMQ(j − k + 1, j)
(these two queries take O(1) time)
This takes O(1) time but why does it work?
i j
k
k

115. More space, faster queries
A
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k
Compute the minimum of RMQ(i, i + k − 1) and RMQ(j − k + 1, j)
(these two queries take O(1) time)
This takes O(1) time but why does it work?
i j
k
k
these overlap
because 2k >

116. More space, faster queries
A
we build Rk for k = 2, 4, 8, 16 . . . n
Rk stores RMQ(i, i + k − 1) for all i,
How do we compute RMQ(i, j)?
If the interval length, = (j − i + 1), is a power-of-two - just look up the answer
these queries take O(1) time
Otherwise, find the k = 2, 4, 8, 16 . . . such that k < 2k
Compute the minimum of RMQ(i, i + k − 1) and RMQ(j − k + 1, j)
(these two queries take O(1) time)
This takes O(1) time but why does it work?
i j
k
k
these overlap
because 2k >
the min is either in
here or in here

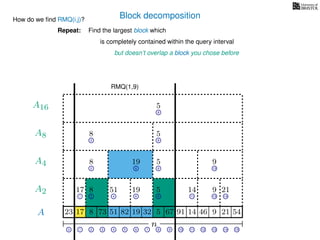
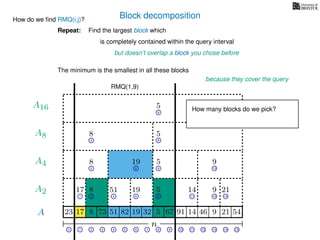
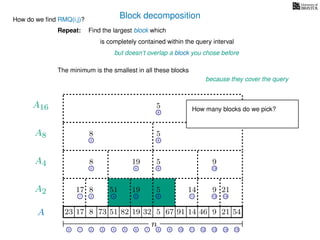
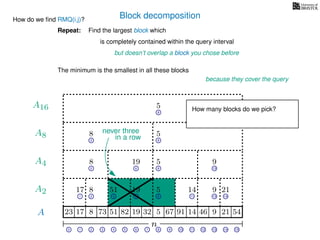
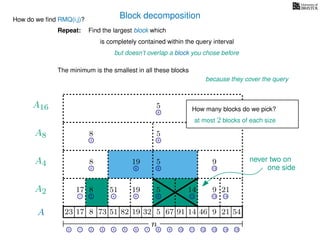
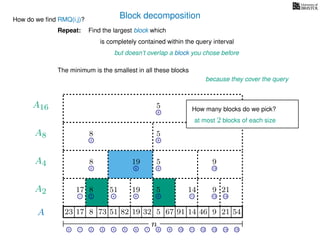
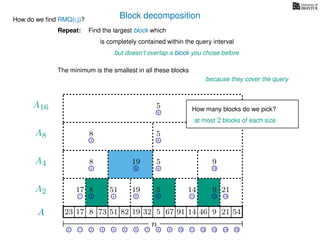
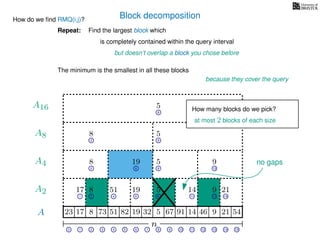
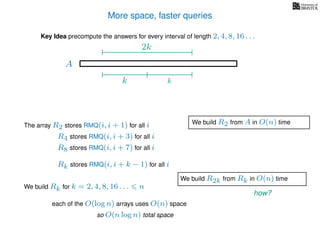
117. Range minimum query (intermediate) summary
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
RMQ(3, 7) = 6
19 9 21 54
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

118. Range minimum query (intermediate) summary
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
RMQ(3, 7) = 6
19 9 21 54
Solution 1
O(n) space
O(n) prep time
O(log n) query time
Solution 2
O(n log n) space
O(n log n) prep time
O(1) query time
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

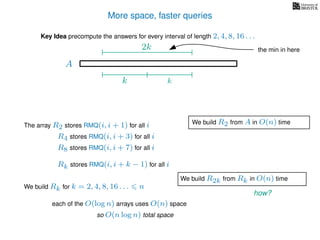
119. Range minimum query (intermediate) summary
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
RMQ(3, 7) = 6
19 9 21 54
Can we do better?
Solution 1
O(n) space
O(n) prep time
O(log n) query time
Solution 2
O(n log n) space
O(n log n) prep time
O(1) query time
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

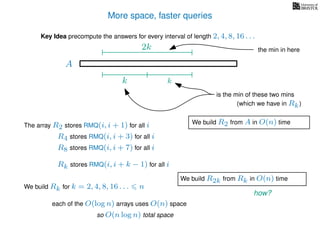
120. Range minimum query (intermediate) summary
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
RMQ(3, 7) = 6
19 9 21 54
Can we do better?
Solution 1
O(n) space
O(n) prep time
O(log n) query time
Solution 2
O(n log n) space
O(n log n) prep time
O(1) query time
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
(yes)

121. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
n

122. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
n

123. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
n
˜n = n
log n

124. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
log n
n
˜n = n
log n

125. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
log n
the smallest of these
is stored here
n
˜n = n
log n

126. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
n
˜n = n
log n

127. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
L0
L1
L2
L3
L4
L5 L˜n

128. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
L0
L1
L2
L3
L4
L5 L˜n

129. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
all of these
are stored here
L0
L1
L2
L3
L4
L5 L˜n

130. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
L0
L1
L2
L3
L4
L5 L˜n

131. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
L0
L1
L2
L3
L4
L5 L˜n

132. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2
L0
L1
L2
L3
L4
L5 L˜n

133. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2
Solution 2 on A
O(n log n) prep time
O(1) query time
O(n log n) space
Recall. . .
L0
L1
L2
L3
L4
L5 L˜n

134. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2
Solution 2 on A
O(n log n) prep time
O(1) query time
O(n log n) space
Recall. . .
L0
L1
L2
L3
L4
L5 L˜n

135. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2
Solution 2 on A
O(n log n) prep time
O(1) query time
O(n log n) space
Recall. . .
Solution 2 on H
O(˜n log ˜n) prep time
O(1) query time
O(˜n log ˜n) space
L0
L1
L2
L3
L4
L5 L˜n

136. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2
Solution 2 on A
O(n log n) prep time
O(1) query time
O(n log n) space
Recall. . .
Solution 2 on H
O(˜n log ˜n) prep time
O(1) query time
O(˜n log ˜n) space = O n
log n log n
log n
L0
L1
L2
L3
L4
L5 L˜n

137. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2
Solution 2 on A
O(n log n) prep time
O(1) query time
O(n log n) space
Recall. . .
Solution 2 on H
O(˜n log ˜n) prep time
O(1) query time
O(˜n log ˜n) space = O n
log n log n
log n = O(n)
L0
L1
L2
L3
L4
L5 L˜n

138. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2
Solution 2 on A
O(n log n) prep time
O(1) query time
O(n log n) space
Recall. . .
Solution 2 on H
O(˜n log ˜n) prep time
O(1) query time
O(˜n log ˜n) space = O n
log n log n
log n = O(n)
= O(n)
L0
L1
L2
L3
L4
L5 L˜n

139. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2
Solution 2 on A
O(n log n) prep time
O(1) query time
O(n log n) space
Recall. . .
Solution 2 on H
O(˜n log ˜n) prep time
O(1) query time
O(˜n log ˜n) space = O n
log n log n
log n = O(n)
= O(n)
in O(n) space/prep time
L0
L1
L2
L3
L4
L5 L˜n

140. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2 in O(n) space/prep time
L0
L1
L2
L3
L4
L5 L˜n

141. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2 in O(n) space/prep time
Preprocess each array Li (which has length log n) to answer RMQs. . .
using Solution 2
L0
L1
L2
L3
L4
L5 L˜n

142. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2 in O(n) space/prep time
Preprocess each array Li (which has length log n) to answer RMQs. . .
using Solution 2
Solution 2 on Li
O(1) query timeO((log n) log log n)) space/prep time
L0
L1
L2
L3
L4
L5 L˜n

143. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2 in O(n) space/prep time
Preprocess each array Li (which has length log n) to answer RMQs. . .
using Solution 2 in O(log n log log n) space/prep time
Solution 2 on Li
O(1) query timeO((log n) log log n)) space/prep time
L0
L1
L2
L3
L4
L5 L˜n

144. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2 in O(n) space/prep time
Preprocess each array Li (which has length log n) to answer RMQs. . .
using Solution 2 in O(log n log log n) space/prep time
Total space = O(n) + O(˜n log n log log n)
L0
L1
L2
L3
L4
L5 L˜n

145. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2 in O(n) space/prep time
Preprocess each array Li (which has length log n) to answer RMQs. . .
using Solution 2 in O(log n log log n) space/prep time
Total space = O(n) + O(˜n log n log log n)
space for RMQ structures
for all the Li arrays
space for RMQ structure for H
L0
L1
L2
L3
L4
L5 L˜n

146. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2 in O(n) space/prep time
Preprocess each array Li (which has length log n) to answer RMQs. . .
using Solution 2 in O(log n log log n) space/prep time
Total space = O(n) + O(˜n log n log log n)
space for RMQ structures
for all the Li arrays
space for RMQ structure for H
= O(n log log n)
L0
L1
L2
L3
L4
L5 L˜n

147. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2 in O(n) space/prep time
Preprocess each array Li (which has length log n) to answer RMQs. . .
using Solution 2 in O(log n log log n) space/prep time
Total space = O(n) + O(˜n log n log log n) = O(n log log n)
L0
L1
L2
L3
L4
L5 L˜n

148. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
Preprocess the array H (which has length ˜n = n
log n ) to answer RMQs. . .
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
using Solution 2 in O(n) space/prep time
Preprocess each array Li (which has length log n) to answer RMQs. . .
using Solution 2 in O(log n log log n) space/prep time
Total space = O(n) + O(˜n log n log log n) = O(n log log n)
Total prep. time = O(n log log n)
L0
L1
L2
L3
L4
L5 L˜n

149. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
L0
L1
L2
L3
L4
L5 L˜n

150. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
L0
L1
L2
L3
L4
L5 L˜n

151. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
L0
L1
L2
L3
L4
L5 L˜n

152. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li
then take the smallest
L0
L1
L2
L3
L4
L5 L˜n

153. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li
then take the smallest
L0
L1
L2
L3
L4
L5 L˜n

154. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li
then take the smallest
i j
L0
L1
L2
L3
L4
L5 L˜n

155. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li
then take the smallest
i = i
log n j = j
log n
i j
L0
L1
L2
L3
L4
L5 L˜n

156. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li
then take the smallest
i = i
log n j = j
log n
i j
indices into H
L0
L1
L2
L3
L4
L5 L˜n

157. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li
then take the smallest
i = i
log n j = j
log n
i j
L0
L1
L2
L3
L4
L5 L˜n

158. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li
then take the smallest
i = i
log n j = j
log n
i j
L0
L1
L2
L3
L4
L5 L˜n

159. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li
then take the smallest
i = i
log n j = j
log n
i j
L0
L1
L2
L3
L4
L5 L˜n

160. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li (here we query L1 and L5)
then take the smallest
i = i
log n j = j
log n
i j
L0
L1
L2
L3
L4
L5 L˜n

161. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li (here we query L1 and L5)
This takes O(1) total query timethen take the smallest
i = i
log n j = j
log n
i j
L0
L1
L2
L3
L4
L5 L˜n

162. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li (here we query L1 and L5)
This takes O(1) total query timethen take the smallest
i = i
log n j = j
log n
i j
L0
L1
L2
L3
L4
L5 L˜n

163. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li (here we query L1 and L5)
This takes O(1) total query timethen take the smallest
i = i
log n j = j
log n
i j
Solution 3
O(n log log n) space O(n log log n) prep time O(1) query time
L0
L1
L2
L3
L4
L5 L˜n

164. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li (here we query L1 and L5)
This takes O(1) total query timethen take the smallest
i = i
log n j = j
log n
i j
Solution 4
O(n log log log n) space O(n log log log n) prep time O(1) query time
L0
L1
L2
L3
L4
L5 L˜n

165. Low-resolution RMQ
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
˜n = n
log n
How do we answer a query in A?
Do at most one query in H. . .
and one query in at most two different Li (here we query L1 and L5)
This takes O(1) total query timethen take the smallest
i = i
log n j = j
log n
i j
Solution 4
O(n log log log n) space O(n log log log n) prep time O(1) query time
how?
L0
L1
L2
L3
L4
L5 L˜n

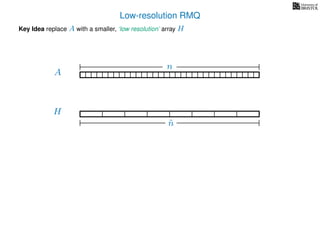
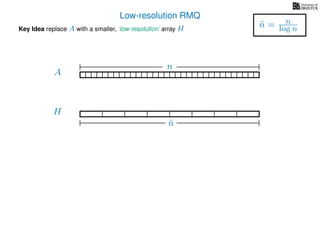
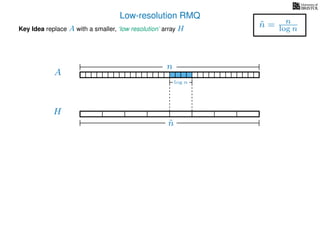
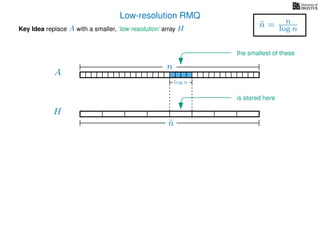
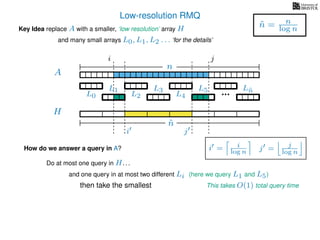
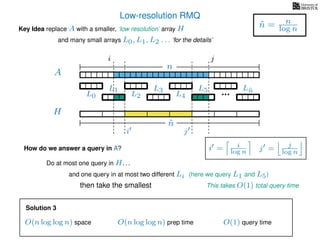
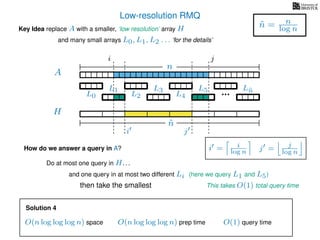
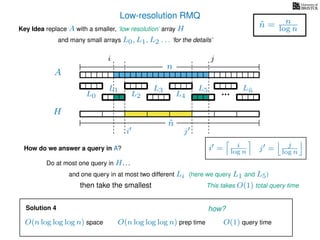
166. Range minimum query summary
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
RMQ(3, 7) = 6
19 9 21 54
Solution 1
O(n) space
O(n) prep time
O(log n) query time
Solution 2
O(n log n) space
O(n log n) prep time
O(1) query time
Solution 3
O(n log log n) space
O(n log log n) prep time
O(1) query time
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

167. Range minimum query summary
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
RMQ(3, 7) = 6
19 9 21 54
Can we do O(n) space and O(1) query time?
Solution 1
O(n) space
O(n) prep time
O(log n) query time
Solution 2
O(n log n) space
O(n log n) prep time
O(1) query time
Solution 3
O(n log log n) space
O(n log log n) prep time
O(1) query time
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

168. Range minimum query summary
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
RMQ(3, 7) = 6
19 9 21 54
Can we do O(n) space and O(1) query time? Yes. . .
Solution 1
O(n) space
O(n) prep time
O(log n) query time
Solution 2
O(n log n) space
O(n log n) prep time
O(1) query time
Solution 3
O(n log log n) space
O(n log log n) prep time
O(1) query time
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

169. Range minimum query summary
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
RMQ(3, 7) = 6
19 9 21 54
Can we do O(n) space and O(1) query time? Yes. . . but not until next lecture
Solution 1
O(n) space
O(n) prep time
O(log n) query time
Solution 2
O(n log n) space
O(n log n) prep time
O(1) query time
Solution 3
O(n log log n) space
O(n log log n) prep time
O(1) query time
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15