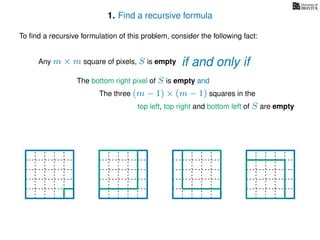
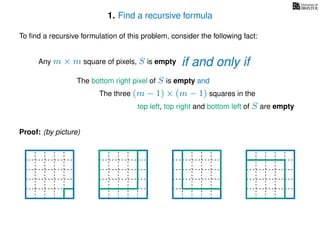
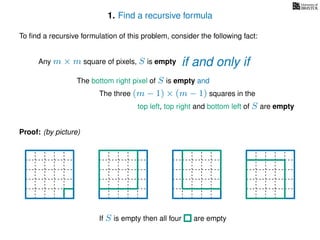
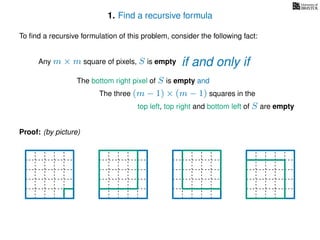
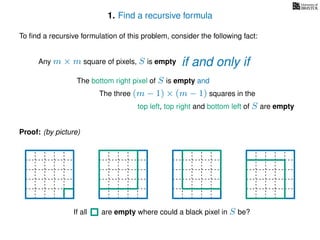
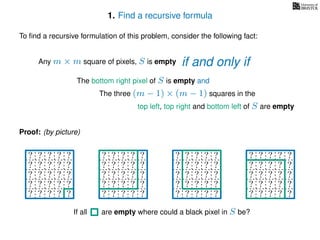
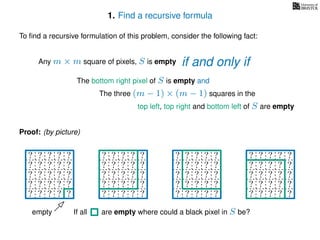
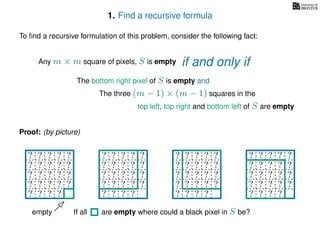
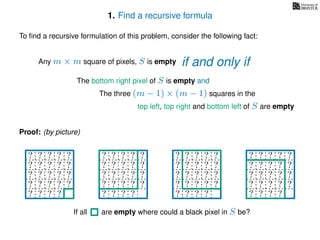
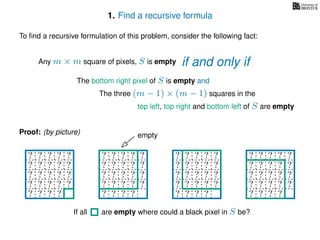
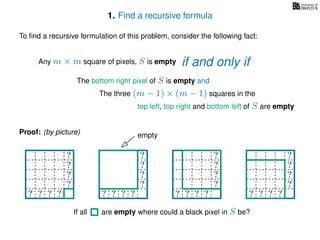
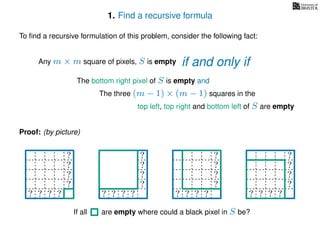
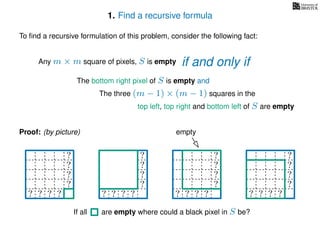
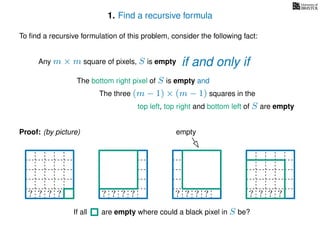
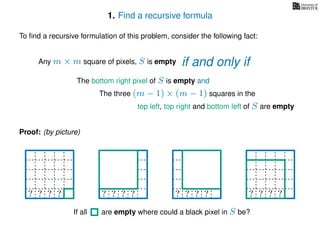
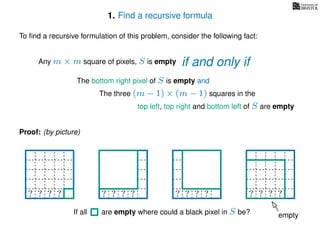
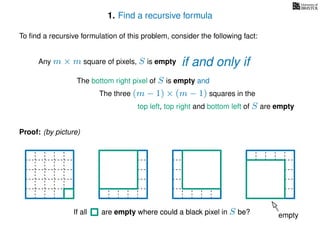
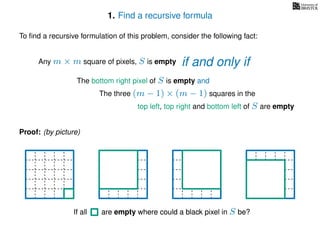
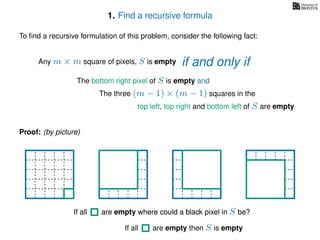
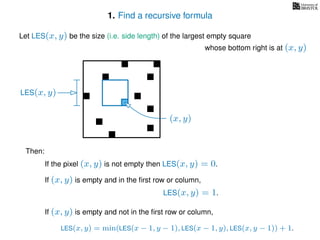
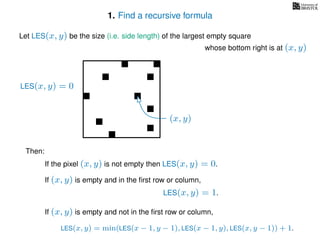
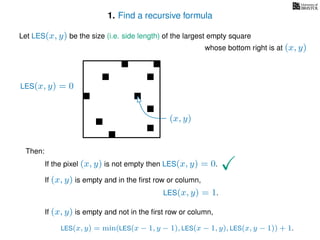
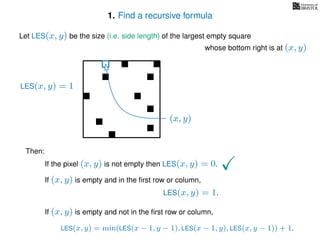
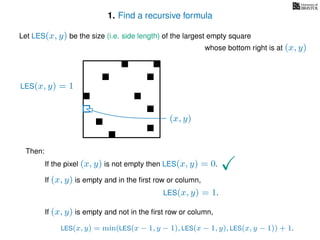
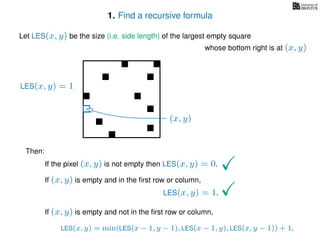
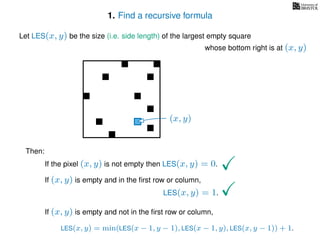
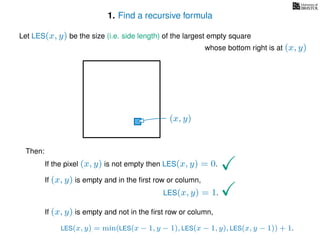
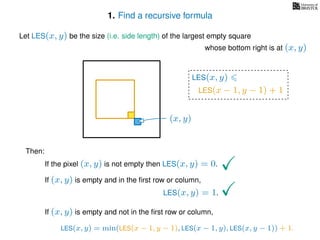
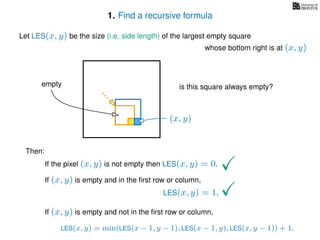
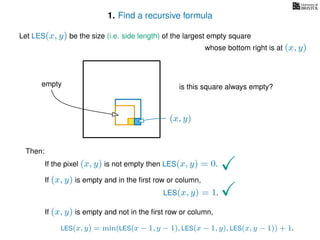
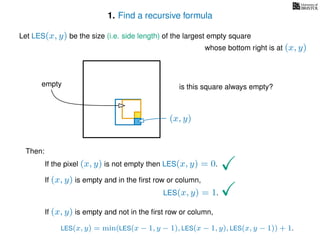
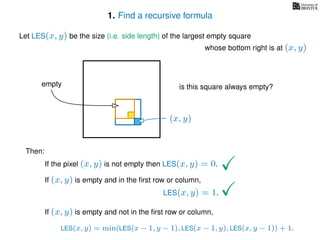
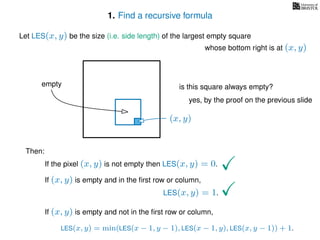
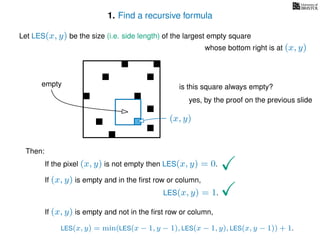
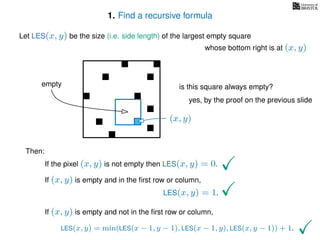
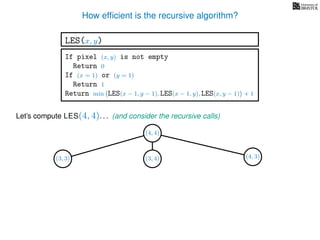
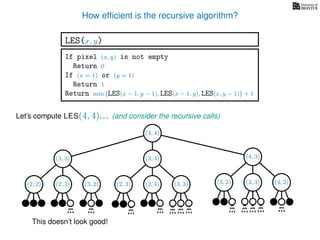
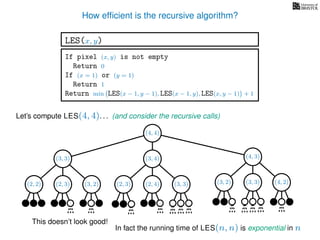
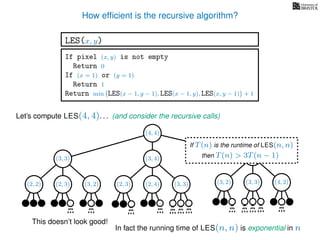
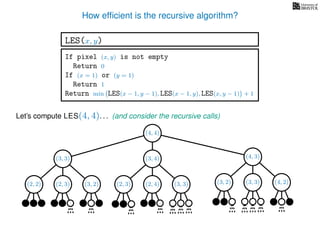
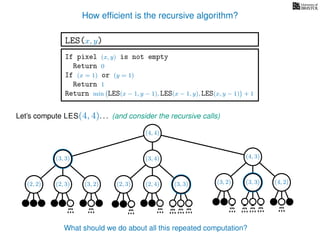
The document discusses dynamic programming, an algorithm design approach invented by Richard Bellman in the 1950s, which solves complex problems by breaking them down into simpler, overlapping subproblems. It introduces applications of dynamic programming, such as finding the largest empty square in a binary image and other problems like the traveling salesman and knapsack problems. The text emphasizes a recursive formula method to achieve efficient algorithmic solutions.

1. Data Structures and Algorithms – COMS21103
Dynamic Programming
Largest Empty Square and Weighted Interval Scheduling
Benjamin Sach

2. The name
Dynamic Programming is an approach to algorithm design. . .
why does it sound like an alternative to Agile Software Development?

3. The name
Dynamic Programming is an approach to algorithm design. . .
why does it sound like an alternative to Agile Software Development?
- Richard Bellman invented Dynamic programming around 1950
a ‘program’ referred to finding an optimal schedule or programme of activities
Serious answer:

4. The name
Dynamic Programming is an approach to algorithm design. . .
why does it sound like an alternative to Agile Software Development?
- Richard Bellman invented Dynamic programming around 1950
“The 1950s were not good years for mathematical research. We had a very interesting
gentleman in Washington named Wilson. He was Secretary of Defense, and he actually had a
pathological fear and hatred of the word, research... His face would suffuse, he would turn red,
and he would get violent if people used the term, research, in his presence. You can imagine
how he felt, then, about the term, mathematical... I thought dynamic programming was a good
name. It was something not even a Congressman could object to.”
a ‘program’ referred to finding an optimal schedule or programme of activities
Serious answer:
Real answer:
- Richard Bellman

5. What problems can Dynamic Programming solve?
• Longest Common Subsequence
• Edit Distance
• Text justification
• Seam Carving
• Solving the Towers of Hanoi
• Predicting cricket scores
• Assembly Line Scheduling
• Matrix Chain Multiplication
• Playing Tetris perfectly
• Dynamic Time Warping
• Finding optimal Binary Search Trees
• The Travelling Salesman Problem
• Knapsack
(used heavily in Bioinformatics for DNA similarity)
(Google this later, it’s really awesome)
(though still slowly)
(when you know the likely frequencies of searches)
(though still slowly)
(used heavily in Bioinformatics for sequence alignment)
(used extensively in computer vision)
and loads of other problems

6. Introduction
Dynamic programming is recursion without repetition
Dynamic programming is a technique for finding efficient algorithms for problems which
can be broken down into simpler, overlapping subproblems.
in other words. . .
The basic idea:
1. Find a recursive formula for the problem
(typically this is the hard bit)
3. Speed it up by storing the solutions to subproblems
(to avoid recomputing the same thing over and over)
4. Derive an iterative algorithm by solving the subproblems in a good order
(iterative algorithms are often better in practice, easier to analyse and prettier)
- in terms of answers to subproblems.
2. Write down a naive recursive algorithm
(typically this algorithm will take exponential time)

7. Part one
Largest Empty Square

8. Largest Empty Square
Problem Given an n × n monochrome image, find the largest empty square.
i.e. without any black pixels
n
n

9. Largest Empty Square
Problem Given an n × n monochrome image, find the largest empty square.
i.e. without any black pixels
n
n

10. Largest Empty Square
Problem Given an n × n monochrome image, find the largest empty square.
i.e. without any black pixels
n
n
an empty square

11. Largest Empty Square
Problem Given an n × n monochrome image, find the largest empty square.
i.e. without any black pixels
n
n

12. Largest Empty Square
Problem Given an n × n monochrome image, find the largest empty square.
i.e. without any black pixels
n
n

13. Largest Empty Square
Problem Given an n × n monochrome image, find the largest empty square.
i.e. without any black pixels
n
n

14. Largest Empty Square
Problem Given an n × n monochrome image, find the largest empty square.
i.e. without any black pixels
n
n
largest empty square

15. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
if and only if

16. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
if and only if

17. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
If S is empty then all four are empty
if and only if

18. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
if and only if

19. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
If all are empty where could a black pixel in S be?
if and only if

20. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
If all are empty where could a black pixel in S be?
if and only if

21. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
empty If all are empty where could a black pixel in S be?
if and only if

22. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
empty If all are empty where could a black pixel in S be?
if and only if

23. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
If all are empty where could a black pixel in S be?
if and only if

24. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
empty
If all are empty where could a black pixel in S be?
if and only if

25. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture) empty
?
?
?
?
? ? ? ?
?
?
?
?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
?
?
?
?
? ? ? ? ?
If all are empty where could a black pixel in S be?
if and only if

26. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
?
?
?
?
? ? ? ?
?
?
?
?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
?
?
?
?
? ? ? ? ?
If all are empty where could a black pixel in S be?
if and only if

27. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
?
?
?
?
? ? ? ?
?
?
?
?
? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ?
?
?
?
?
? ? ? ? ?
empty
If all are empty where could a black pixel in S be?
if and only if

28. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture) empty
? ? ? ?? ? ? ?? ? ? ?? ? ? ? ?
If all are empty where could a black pixel in S be?
if and only if

29. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
? ? ? ?? ? ? ?? ? ? ?? ? ? ? ?
If all are empty where could a black pixel in S be?
if and only if

30. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
? ? ? ?? ? ? ?? ? ? ?? ? ? ? ?
emptyIf all are empty where could a black pixel in S be?
if and only if

31. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
emptyIf all are empty where could a black pixel in S be?If all are empty where could a black pixel in S be?
if and only if

32. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
If all are empty where could a black pixel in S be?If all are empty where could a black pixel in S be?
if and only if

33. 1. Find a recursive formula
To find a recursive formulation of this problem, consider the following fact:
Any m × m square of pixels, S is empty
The bottom right pixel of S is empty and
The three (m − 1) × (m − 1) squares in the
top left, top right and bottom left of S are empty
Proof: (by picture)
If all are empty then S is empty
If all are empty where could a black pixel in S be?If all are empty where could a black pixel in S be?
if and only if

34. 1. Find a recursive formula
(x, y)
LES(x, y)
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.

35. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
LES(x, y) = 0

36. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
LES(x, y) = 0

37. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
LES(x, y) = 1
(x, y)

38. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
LES(x, y) = 1
(x, y)

39. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
LES(x, y) = 1
(x, y)

40. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)

41. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)

42. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y)
(x, y)
LES(x − 1, y − 1) + 1
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.

43. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y)
(x, y)
LES(x − 1, y − 1) + 1
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.

44. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y)
(x, y)
LES(x − 1, y − 1) + 1
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
can’t be bigger
than this
LES(x, y)

45. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y)
(x, y)
LES(x − 1, y − 1) + 1
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
can’t be bigger
than this
LES(x, y)

46. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y)
(x, y)
LES(x − 1, y − 1) + 1
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
can’t be bigger
than this
there is a non-empty
pixel in here
LES(x, y)

47. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
(x, y)
LES(x, y)
LES(x − 1, y) + 1
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
can’t be bigger
than this
LES(x, y)

48. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
(x, y)
LES(x, y)
LES(x, y − 1) + 1
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
can’t be bigger
than this
LES(x, y)

49. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
can’t be bigger
than this
LES(x, y)

50. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?
can’t be bigger
than this
LES(x, y)

51. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?

52. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?empty

53. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?empty

54. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?empty

55. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?empty

56. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?empty

57. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?empty

58. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?empty

59. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?empty

60. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?empty

61. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?empty

62. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?
yes, by the proof on the previous slide
empty

63. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?
yes, by the proof on the previous slide
empty

64. 1. Find a recursive formula
Let LES(x, y) be the size (i.e. side length) of the largest empty square
whose bottom right is at (x, y)
Then:
If the pixel (x, y) is not empty then LES(x, y) = 0.
If (x, y) is empty and in the first row or column,
LES(x, y) = 1.
If (x, y) is empty and not in the first row or column,
LES(x, y) = min(LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1)) + 1.
(x, y)
is this square always empty?
yes, by the proof on the previous slide
empty

65. 2. Write down a recursive algorithm
We can use the recursive formula to get a recursive algorithm. . .
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
LES(x, y) computes the size of the largest empty square
whose bottom right is at (x, y)
Therefore, the maximum of LES(x, y) over all x and y
gives the size of the largest empty square in the whole image

66. 2. Write down a recursive algorithm
We can use the recursive formula to get a recursive algorithm. . .
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
LES(x, y) computes the size of the largest empty square
whose bottom right is at (x, y)
Therefore, the maximum of LES(x, y) over all x and y
gives the size of the largest empty square in the whole image
What is the time complexity of this algorithm?

67. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .

68. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . . (and consider the recursive calls)

69. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)

70. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)(3, 3)

71. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)

72. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4)
(3, 3)
(3, 3) (3, 3) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)

73. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4)
(3, 3)
(3, 3) (3, 3) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)
computed three times :s

74. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)

75. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)

76. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)

77. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)
(2, 2) is computed three times just while computing this (3, 3)

78. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)

79. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)
This doesn’t look good!

80. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)
This doesn’t look good!
In fact the running time of LES(n, n) is exponential in n

81. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)
This doesn’t look good!
In fact the running time of LES(n, n) is exponential in n
If T(n) is the runtime of LES(n, n)
then T(n) > 3T(n − 1)

82. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)

83. How efficient is the recursive algorithm?
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
Return min LES(x − 1, y − 1), LES(x − 1, y), LES(x, y − 1) + 1
LES(x, y)
Let’s compute LES(4, 4). . .
(4, 4)
(and consider the recursive calls)
(4, 3)(3, 4)
(2, 2) (2, 3) (3, 2) (2, 3) (2, 4)
(3, 3)
(3, 3) (3, 3) (4, 2)(3, 3)(3, 2)(3, 3)
(3, 3)
What should we do about all this repeated computation?

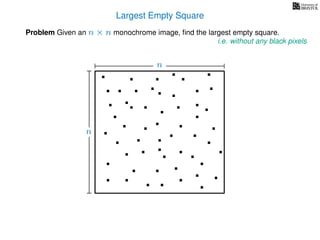
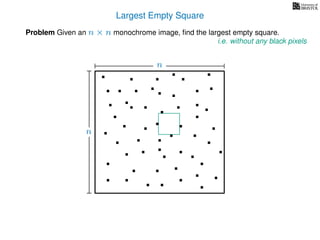
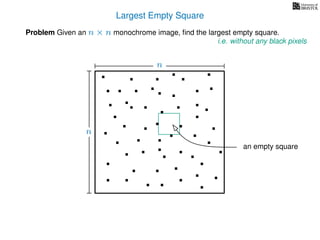
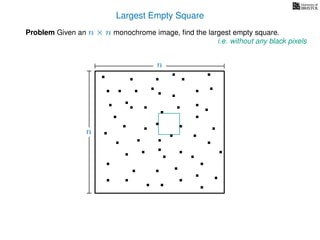
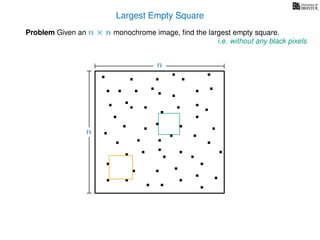
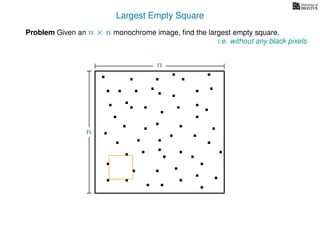
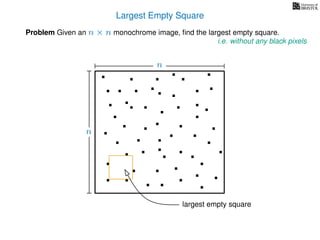
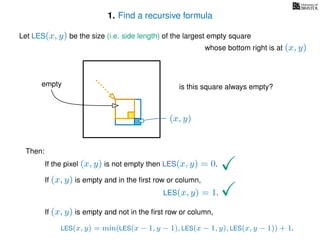
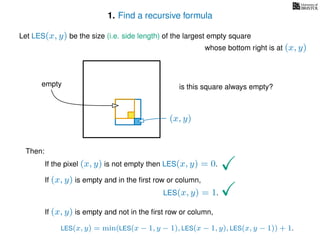
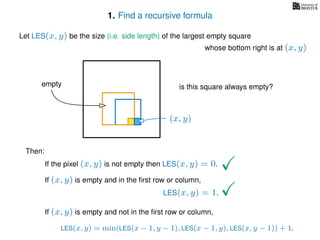
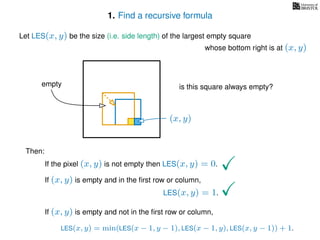
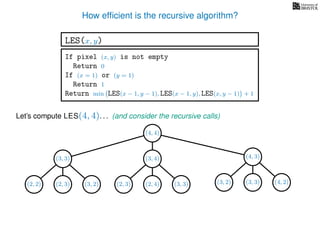
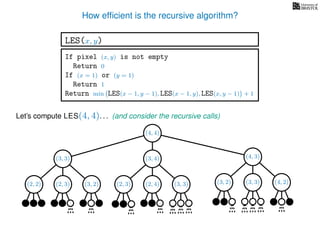
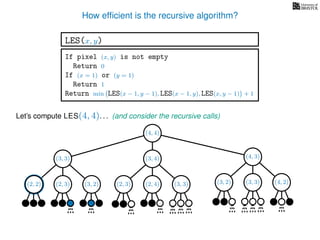
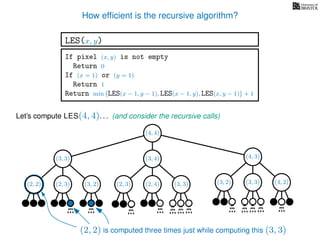
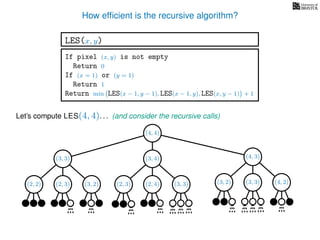
84. 3. Store the solutions to subproblems
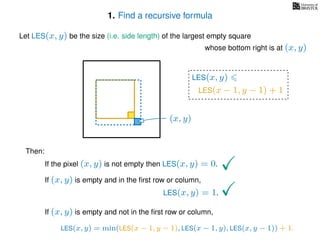
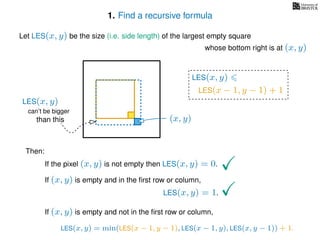
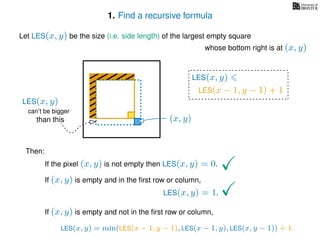
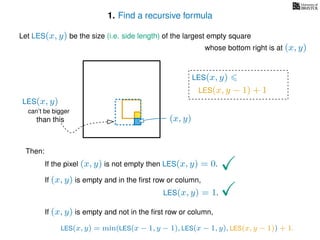
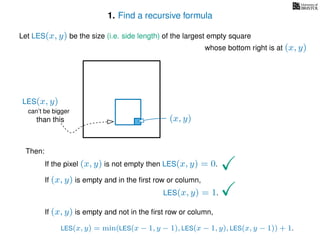
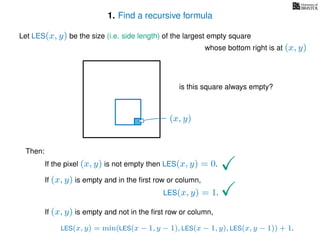
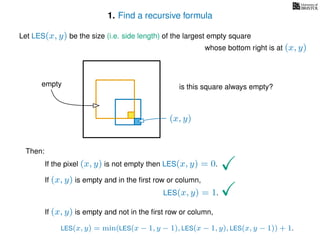
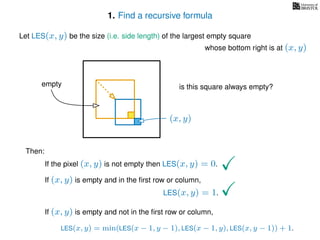
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
If LES[x, y] undefined
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
Return LES[x, y]
MemLES(x, y)
In the MemLES version of the algorithm
we store solutions to previously computed subproblems
in an (n × n) 2D array called LES

85. 3. Store the solutions to subproblems
This is called memoization (not memorization)
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
If LES[x, y] undefined
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
Return LES[x, y]
MemLES(x, y)
In the MemLES version of the algorithm
we store solutions to previously computed subproblems
in an (n × n) 2D array called LES

86. 3. Store the solutions to subproblems
This is called memoization (not memorization)
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
If LES[x, y] undefined
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
Return LES[x, y]
MemLES(x, y)
In the MemLES version of the algorithm
we store solutions to previously computed subproblems
in an (n × n) 2D array called LES
Crucially, now each entry LES[x, y] is only computed once

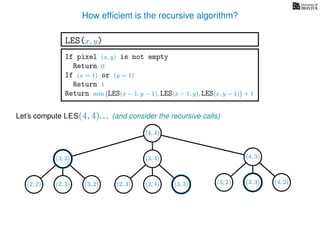
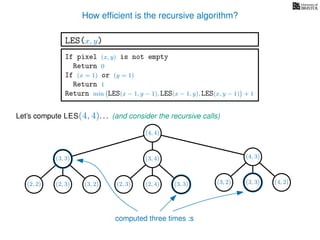
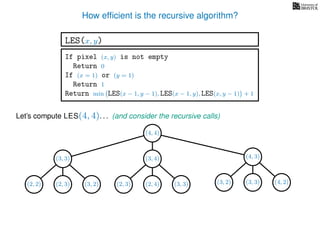
87. 3. Store the solutions to subproblems
This is called memoization (not memorization)
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
If LES[x, y] undefined
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
Return LES[x, y]
MemLES(x, y)
In the MemLES version of the algorithm
we store solutions to previously computed subproblems
in an (n × n) 2D array called LES
Crucially, now each entry LES[x, y] is only computed once
The time complexity of computing MemLES(n, n) is now O(n2)

88. 3. Store the solutions to subproblems
This is called memoization (not memorization)
If pixel (x, y) is not empty
Return 0
If (x = 1) or (y = 1)
Return 1
If LES[x, y] undefined
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
Return LES[x, y]
MemLES(x, y)
In the MemLES version of the algorithm
we store solutions to previously computed subproblems
in an (n × n) 2D array called LES
Crucially, now each entry LES[x, y] is only computed once
The time complexity of computing MemLES(n, n) is now O(n2)
in fact, computing maxx,y MemLES(x, y) takes O(n2) time too

89. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
LES[n, n]
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

90. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
LES[n, n]
What information do we need to compute LES[n, n]?
to compute
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

91. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
LES[n, n]
What information do we need to compute LES[n, n]?
to compute
The 2D array
LES:
we need
(for x, y > 1 and (x, y) non empty)

92. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
LES[n, n]
What information do we need to compute LES[n, n]?
to compute
The 2D array
LES:
we need
LES[n − 1, n − 1]
LES[n − 1, n]
and LES[n, n − 1]
(for x, y > 1 and (x, y) non empty)

93. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
LES[n, n]
What information do we need to compute LES[n, n]?
to compute
The 2D array
LES:
we need
LES[n − 1, n − 1]
LES[n − 1, n]
and LES[n, n − 1]
(for x, y > 1 and (x, y) non empty)

94. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
LES[n, n − 1]
to compute
(for x, y > 1 and (x, y) non empty)

95. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
LES[n, n − 1]
to compute
(for x, y > 1 and (x, y) non empty)

96. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
LES[n, n − 1]
to compute
LES[n − 1, n − 1]
and LES[n, n − 2]
LES[n − 1, n − 2]
(for x, y > 1 and (x, y) non empty)

97. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
LES[n, n − 1]
to compute
LES[n − 1, n − 1]
and LES[n, n − 2]
LES[n − 1, n − 2]
(for x, y > 1 and (x, y) non empty)

98. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
LES[n − 1, n]
to compute
(for x, y > 1 and (x, y) non empty)

99. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
we need
LES[n − 1, n]
to compute
(for x, y > 1 and (x, y) non empty)

100. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
we need
LES[n − 1, n]
to compute
LES[n − 2, n]
and LES[n − 1, n − 1]
LES[n − 2, n − 1]
(for x, y > 1 and (x, y) non empty)

101. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
we need
LES[n − 1, n]
to compute
LES[n − 2, n]
and LES[n − 1, n − 1]
LES[n − 2, n − 1]
(for x, y > 1 and (x, y) non empty)

102. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

103. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

104. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

105. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

106. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

107. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

108. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

109. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

110. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

111. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

112. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

113. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

114. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

115. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

116. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

117. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

118. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

119. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

120. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

121. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES:
(for x, y > 1 and (x, y) non empty)

122. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
(for x, y > 1 and (x, y) non empty)

123. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

124. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

125. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

126. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

127. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

128. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

129. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

130. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

131. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

132. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

133. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

134. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

135. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

136. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

137. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

138. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

139. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

140. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

141. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

142. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

143. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

144. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

145. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

146. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

147. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

148. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

149. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

150. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

151. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

152. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

153. The dependency graph
LES[x, y]= min MemLES(x − 1, y − 1), MemLES(x − 1, y), MemLES(x, y − 1) + 1
What information do we need to compute LES[n, n]?
The 2D array
LES: How can we use this to get an
iterative algorithm?
Fill in the array from
the top-left!
(for x, y > 1 and (x, y) non empty)

154. 4. Derive an iterative algorithm
For y = 1 to n
For x = 1 to n
If pixel (x, y) is not empty
LES[x, y] = 0
Else If (x = 1) or (y = 1)
LES[x, y] = 1
Else
LES[x, y]= min LES[x − 1, y − 1], LES[x − 1, y], LES[x, y − 1] + 1
ItLES(n)
This iterative version of the algorithm
runs in O(n2) time
and avoids making any recursive calls

155. 4. Derive an iterative algorithm
For y = 1 to n
For x = 1 to n
If pixel (x, y) is not empty
LES[x, y] = 0
Else If (x = 1) or (y = 1)
LES[x, y] = 1
Else
LES[x, y]= min LES[x − 1, y − 1], LES[x − 1, y], LES[x, y − 1] + 1
ItLES(n)
This iterative version of the algorithm
runs in O(n2) time
and avoids making any recursive calls
Maximum of LES[x, y] over all x and y
gives the size of the largest empty square in the whole image
this also takes O(n2) time

156. Introduction
Dynamic programming is recursion without repetition
Dynamic programming is a technique for finding efficient algorithms for problems which
can be broken down into simpler, overlapping subproblems.
in other words. . .
The basic idea:
1. Find a recursive formula for the problem
(typically this is the hard bit)
3. Speed it up by storing the solutions to subproblems (memoization)
(to avoid recomputing the same thing over and over)
4. Derive an iterative algorithm by solving the subproblems in a good order
(iterative algorithms are often better in practice, easier to analyse and prettier)
- in terms of answers to subproblems.
2. Write down a naive recursive algorithm
(typically this algorithm will take exponential time)
Summary

157. End of part one

158. Part two
Weighted Interval Scheduling

159. Introduction
Dynamic programming is recursion without repetition
Dynamic programming is a technique for finding efficient algorithms for problems which
can be broken down into simpler, overlapping subproblems.
in other words. . .
The basic idea:
1. Find a recursive formula for the problem
(typically this is the hard bit)
3. Speed it up by storing the solutions to subproblems (memoization)
(to avoid recomputing the same thing over and over)
4. Derive an iterative algorithm by solving the subproblems in a good order
(iterative algorithms are often better in practice, easier to analyse and prettier)
- in terms of answers to subproblems.
2. Write down a naive recursive algorithm
(typically this algorithm will take exponential time)
Summary
Introduction

160. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5

161. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
66

162. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
66
start time

163. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
66
start time
finish time

164. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
66
start time
finish timeweight

165. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
start time
finish timeweight

166. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6

167. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6 4

168. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
compatible intervals don’t overlap
4

169. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
1
incompatible intervals overlap

170. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
1
incompatible intervals overlap
Two intervals are compatible if they don’t overlap

171. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
4
weight
Two intervals are compatible if they don’t overlap

172. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
4
weight
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals

173. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
a schedule
3 2
4

174. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
4
weight
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
a different schedule
2
1 7

175. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
4
weight
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals

176. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
4
weight
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
The weight of a schedule is the sum of
the weight of the intervals it contains

177. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
The weight of a schedule is the sum of
the weight of the intervals it contains
a schedule
3 2
with total weight 15
4

178. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
The weight of a schedule is the sum of
the weight of the intervals it contains
a different schedule
2
1 7
with total weight 10

179. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
The weight of a schedule is the sum of
the weight of the intervals it contains
a schedule
3 2
with total weight 15
4

180. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
The weight of a schedule is the sum of
the weight of the intervals it contains
a schedule
3 2
with total weight 15
is this the best possible?
4

181. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
The weight of a schedule is the sum of
the weight of the intervals it contains
is this the best possible?
5
6
with total weight 17a schedule
2
4

182. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
The weight of a schedule is the sum of
the weight of the intervals it contains
is this the best possible?
5
6
with total weight 17a schedule
2
4

183. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
The weight of a schedule is the sum of
the weight of the intervals it contains
with total weight 18
7
a schedule
is this the best possible?
5

184. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
The weight of a schedule is the sum of
the weight of the intervals it contains
with total weight 18
7
a schedule
is this the best possible?
5

185. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
time
2
1
3 5 2
4
75
6
4
weight
6
Two intervals are compatible if they don’t overlap
A schedule is a set of compatible intervals
The weight of a schedule is the sum of
the weight of the intervals it contains
with total weight 18
7
a schedule
is this the best possible?
5
yes

186. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
4
weight

187. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
4
weight
How is the input provided?

188. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
4
weight
How is the input provided?
The intervals are given in an array A of length n

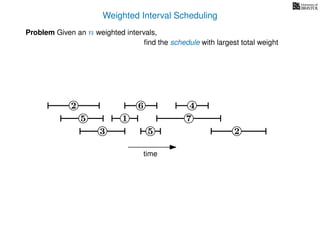
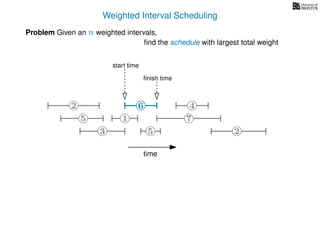
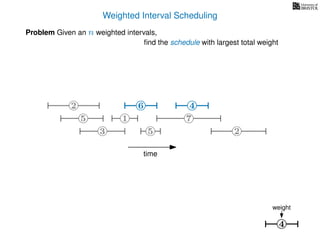
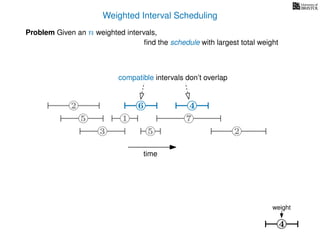
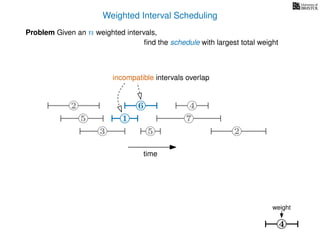
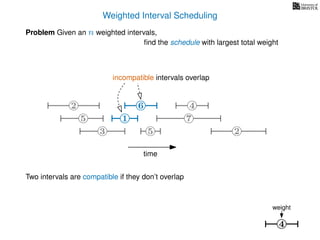
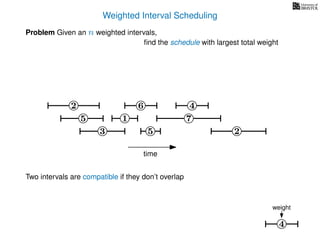
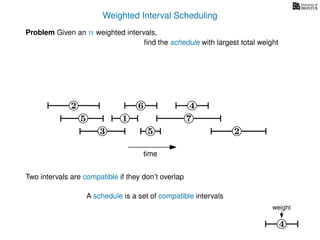
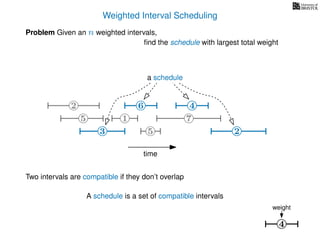
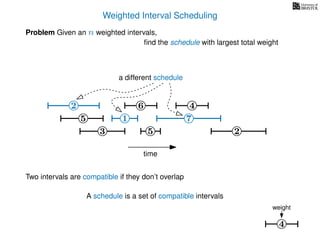
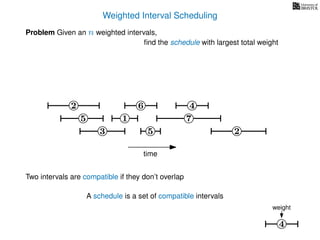
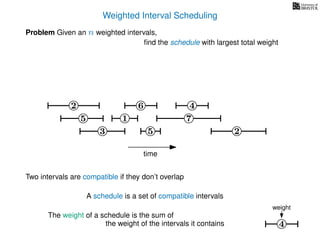
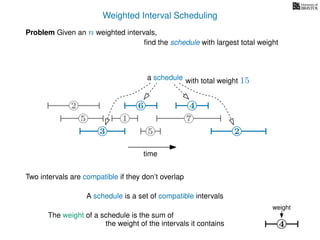
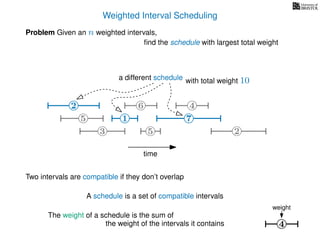
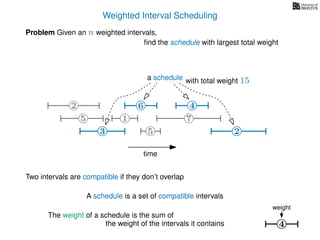
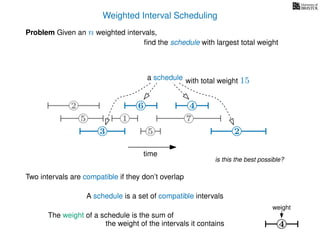
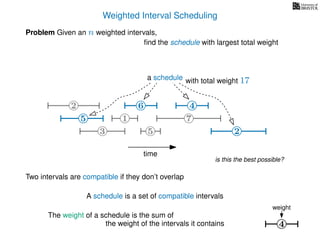
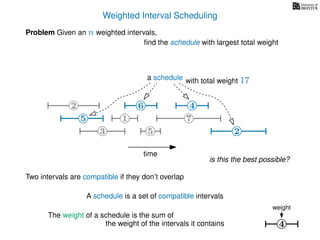
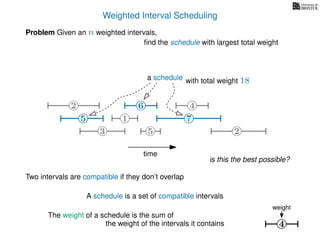
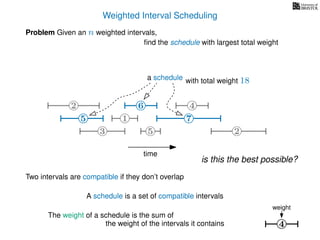
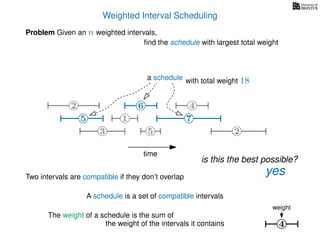
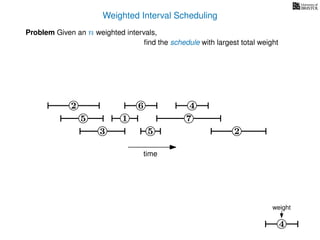
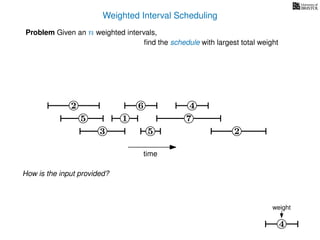
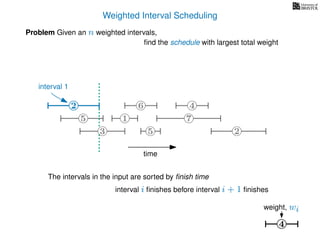
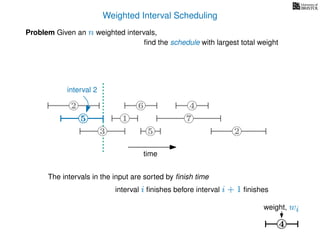
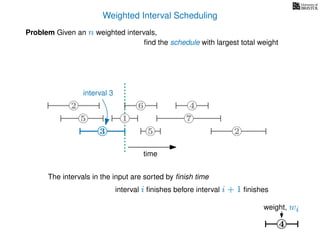
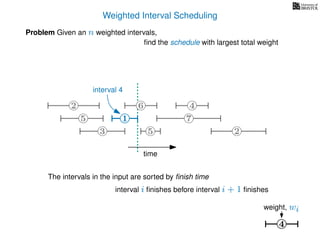
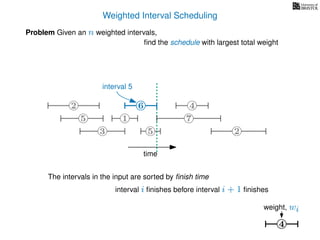
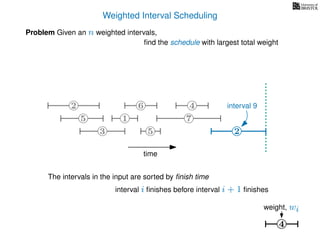
189. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
4
weight
How is the input provided?
The intervals are given in an array A of length n
A[i] stores a triple (si, fi, wi) which defines the i-th interval

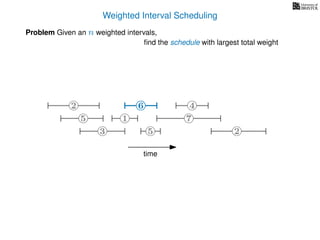
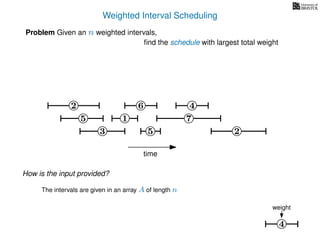
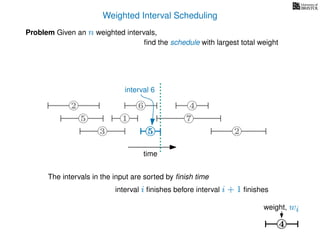
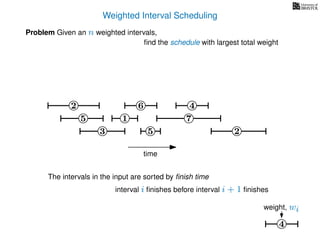
190. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
start time, si
4
weight
How is the input provided?
The intervals are given in an array A of length n
A[i] stores a triple (si, fi, wi) which defines the i-th interval

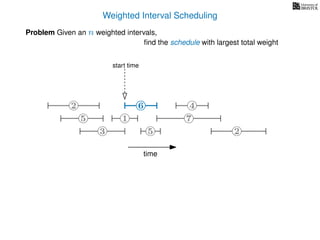
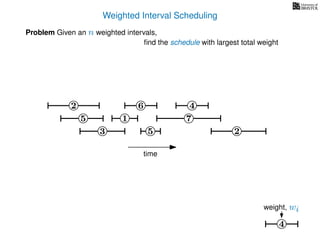
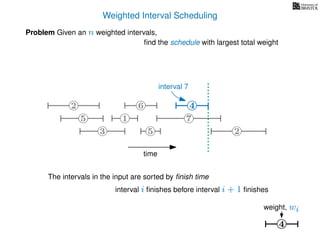
191. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
start time, si
finish time, fi
4
weight
How is the input provided?
The intervals are given in an array A of length n
A[i] stores a triple (si, fi, wi) which defines the i-th interval

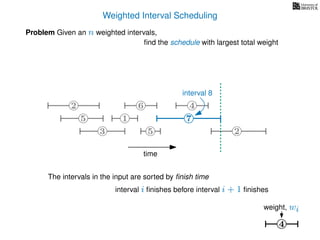
192. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
start time, si
finish time, fiweight, wi
4
weight
How is the input provided?
The intervals are given in an array A of length n
A[i] stores a triple (si, fi, wi) which defines the i-th interval

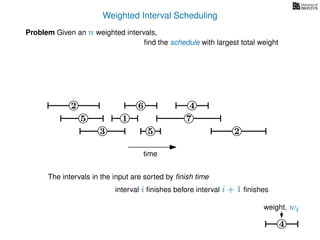
193. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
start time, si
finish time, fiweight, wi
How is the input provided?
The intervals are given in an array A of length n
A[i] stores a triple (si, fi, wi) which defines the i-th interval
4
weight, wi

194. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
7
time
5
start time, si
finish time, fiweight, wi
How is the input provided?
The intervals are given in an array A of length n
A[i] stores a triple (si, fi, wi) which defines the i-th interval
The intervals are sorted by finish time i.e. fi fi+1 4
weight, wi

195. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
75
4
weight, wi
time

196. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
75
4
weight, wi
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

197. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
4
weight, wi
2
1
3 5 2
4
75
62
interval 1
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

198. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
4
weight, wi
2
1
3 5 2
4
75
6
5
interval 2
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

199. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
4
weight, wi
2
1
3 5 2
4
75
6
3
interval 3
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

200. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
4
weight, wi
2
1
3 5 2
4
75
6
1
interval 4
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

201. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
4
weight, wi
2
1
3 5 2
4
75
66
interval 5
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

202. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
4
weight, wi
2
1
3 5 2
4
75
6
5
interval 6
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

203. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
4
weight, wi
2
1
3 5 2
4
75
6 4
interval 7
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

204. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
4
weight, wi
2
1
3 5 2
4
75
6
7
interval 8
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

205. Weighted Interval Scheduling
Problem Given an n weighted intervals,
find the schedule with largest total weight
4
weight, wi
2
1
3 5 2
4
75
6
2
interval 9
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

206. Weighted Interval Scheduling
6
Problem Given an n weighted intervals,
find the schedule with largest total weight
2
1
3 5 2
4
75
4
weight, wi
The intervals in the input are sorted by finish time
interval i finishes before interval i + 1 finishes
time

207. Compatible Intervals
interval p(7)
interval 7

208. Compatible Intervals
Let p(i) be the rightmost interval (in order of finish time)
which finishes before the i-th interval but doesn’t overlap it
interval p(7)
interval 7
For all i,

209. Compatible Intervals
Let p(i) be the rightmost interval (in order of finish time)
which finishes before the i-th interval but doesn’t overlap it
For all i,
interval p(4)
interval 4

210. Compatible Intervals
Let p(i) be the rightmost interval (in order of finish time)
which finishes before the i-th interval but doesn’t overlap it
For all i,
interval 2

211. Compatible Intervals
Let p(i) be the rightmost interval (in order of finish time)
which finishes before the i-th interval but doesn’t overlap it
For all i,
interval 2
What is p(2)?

212. Compatible Intervals
Let p(i) be the rightmost interval (in order of finish time)
which finishes before the i-th interval but doesn’t overlap it
For all i,
interval 2
What is p(2)?
if no such interval exists, p(i) = 0

213. Compatible Intervals
Let p(i) be the rightmost interval (in order of finish time)
which finishes before the i-th interval but doesn’t overlap it
interval p(7)
interval 7
For all i,
if no such interval exists, p(i) = 0

214. Compatible Intervals
Let p(i) be the rightmost interval (in order of finish time)
which finishes before the i-th interval but doesn’t overlap it
Claim: We can precompute all p(i) in O(n log n) time
interval p(7)
interval 7
For all i,
if no such interval exists, p(i) = 0

215. Compatible Intervals
Let p(i) be the rightmost interval (in order of finish time)
which finishes before the i-th interval but doesn’t overlap it
Claim: We can precompute all p(i) in O(n log n) time
interval p(7)
interval 7
For all i,
if no such interval exists, p(i) = 0
(and we’ll assume we did this already)

216. Compatible Intervals
Let p(i) be the rightmost interval (in order of finish time)
which finishes before the i-th interval but doesn’t overlap it
Claim: We can precompute all p(i) in O(n log n) time
interval p(7)
interval 7
For all i,
if no such interval exists, p(i) = 0
- we’ll come back to this at the end
(and we’ll assume we did this already)

217. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown

218. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
In particular, consider the n-th interval . . .
more intervals not shown

219. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
In particular, consider the n-th interval . . .
more intervals not shown
n-th interval

220. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval

221. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
Either the n-th interval is in schedule O. . . or it isn’t
more intervals not shown
n-th interval

222. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
Either the n-th interval is in schedule O. . . or it isn’t
this gives us two cases to consider:
more intervals not shown
n-th interval

223. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
Either the n-th interval is in schedule O. . . or it isn’t
this gives us two cases to consider:
more intervals not shown
n-th interval
Case 2: The n-th interval is in O
Case 1: The n-th interval is not in O

224. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Case 1: The n-th interval is not in O

225. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Case 1: The n-th interval is not in O
is not in O

226. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Case 1: The n-th interval is not in O
- schedule O is also an optimal schedule for the problem
with the input consisting of intervals {1, 2, 3 . . . , n − 1}
is not in O

227. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
n-th interval
Case 1: The n-th interval is not in O
- schedule O is also an optimal schedule for the problem
with the input consisting of intervals {1, 2, 3 . . . , n − 1}
is not in O
more intervals not shown

228. 1. Find a recursive formula
so, in this case we have that OPT = OPT(n − 1)
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
n-th interval
Case 1: The n-th interval is not in O
- schedule O is also an optimal schedule for the problem
with the input consisting of intervals {1, 2, 3 . . . , n − 1}
is not in O
more intervals not shown

229. 1. Find a recursive formula
so, in this case we have that OPT = OPT(n − 1)
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
n-th interval
Case 1: The n-th interval is not in O
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
- schedule O is also an optimal schedule for the problem
with the input consisting of intervals {1, 2, 3 . . . , n − 1}
is not in O
more intervals not shown

230. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
Case 2: The n-th interval is in O
is in O

231. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
Case 2: The n-th interval is in O
is in O
The only other intervals which could be in O are {1, 2, 3, . . . p(n)}

232. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
Case 2: The n-th interval is in O
is in O
The only other intervals which could be in O are {1, 2, 3, . . . p(n)}
not in O (they overlap)

233. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
Case 2: The n-th interval is in O
is in O
The only other intervals which could be in O are {1, 2, 3, . . . p(n)}
not in O (they overlap)
more intervals not shown

234. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
Case 2: The n-th interval is in O
is in O
The only other intervals which could be in O are {1, 2, 3, . . . p(n)}
not in O (they overlap)
more intervals not shown
interval p(n)

235. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
Case 2: The n-th interval is in O
is in O
The only other intervals which could be in O are {1, 2, 3, . . . p(n)}
not in O (they overlap)
(the ones which don’t overlap the n-th interval)
more intervals not shown
interval p(n)

236. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
Case 2: The n-th interval is in O
is in O
The only other intervals which could be in O are {1, 2, 3, . . . p(n)}
not in O (they overlap)
(the ones which don’t overlap the n-th interval)
more intervals not shown
for the intervals {1, 2, 3 . . . , p(n)}
Schedule O with interval n removed gives an optimal schedule
interval p(n)

237. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
Case 2: The n-th interval is in O
is in O
The only other intervals which could be in O are {1, 2, 3, . . . p(n)}
not in O (they overlap)
(the ones which don’t overlap the n-th interval)
more intervals not shown
for the intervals {1, 2, 3 . . . , p(n)}
Schedule O with interval n removed gives an optimal schedule
interval p(n)
(wn is the weight of interval n)

238. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
Case 2: The n-th interval is in O
is in O
The only other intervals which could be in O are {1, 2, 3, . . . p(n)}
not in O (they overlap)
(the ones which don’t overlap the n-th interval)
more intervals not shown
for the intervals {1, 2, 3 . . . , p(n)}
Schedule O with interval n removed gives an optimal schedule
interval p(n)
(wn is the weight of interval n)
so we have that OPT = OPT(p(n)) + wn

239. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
(wn is the weight of interval n)
Case 2: The n-th interval is in OCase 1: The n-th interval is not in O
OPT = OPT(n − 1) OPT = OPT(p(n)) + wn

240. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
(wn is the weight of interval n)
Case 2: The n-th interval is in OCase 1: The n-th interval is not in O
OPT = OPT(n − 1) OPT = OPT(p(n)) + wn
Well, which is it?

241. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
(wn is the weight of interval n)
Case 2: The n-th interval is in OCase 1: The n-th interval is not in O
OPT = OPT(n − 1) OPT = OPT(p(n)) + wn
Well, which is it? It’s the bigger one

242. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
(wn is the weight of interval n)
Case 2: The n-th interval is in OCase 1: The n-th interval is not in O
OPT = OPT(n − 1) OPT = OPT(p(n)) + wn
Well, which is it? It’s the bigger one
OPT = max(OPT(n − 1), OPT(p(n)) + wn)

243. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , n} with weight OPT. . .
more intervals not shown
n-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
(wn is the weight of interval n)
Case 2: The n-th interval is in OCase 1: The n-th interval is not in O
OPT = OPT(n − 1) OPT = OPT(p(n)) + wn
Well, which is it? It’s the bigger one
OPT = max(OPT(n − 1), OPT(p(n)) + wn)
(they both always give viable schedules)

244. 1. Find a recursive formula
Consider some optimal schedule O for intervals {1, 2, 3 . . . , i} with weight OPT(i). . .
more intervals not shown
i-th interval
Notation: OPT(i) is the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}
Case 2: The i-th interval is in OCase 1: The i-th interval is not in O
OPT(i) = OPT(i − 1) OPT(i) = OPT(p(i)) + wi
Well, which is it? It’s the bigger one
OPT(i) = max(OPT(i − 1), OPT(p(i)) + wi)
(they both always give viable schedules)
(wi is the weight of interval i)

245. 2. Write down a recursive algorithm
Once again, we can use the recursive formula to get a recursive algorithm. . .
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
Therefore, WIS(n) gives the weight of the optimal schedule
(for the full problem)
WIS(i) computes the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}

246. 2. Write down a recursive algorithm
Once again, we can use the recursive formula to get a recursive algorithm. . .
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
Therefore, WIS(n) gives the weight of the optimal schedule
(for the full problem)
What is the time complexity of this algorithm?
WIS(i) computes the weight of an optimal schedule for intervals {1, 2, 3, . . . , i}

247. How efficient is the recursive algorithm?
consider this simple input with n = 6
1
1
1
1
1
1
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)

248. How efficient is the recursive algorithm?
consider this simple input with n = 6
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
1
1
1
1
1
1
(the best schedule has weight 3)

249. How efficient is the recursive algorithm?
consider this simple input with n = 6
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
1
1
1
1
1
1
(the best schedule has weight 3)
further, for all i, p(i) = i − 2

250. How efficient is the recursive algorithm?
consider this simple input with n = 6
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
1
1
1
1
1
1
(the best schedule has weight 3)
further, for all i, p(i) = i − 2
so WIS(i) makes recursive calls to WIS(i − 1) and WIS(i − 2)

251. How efficient is the recursive algorithm?
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
so WIS(i) makes recursive calls to WIS(i − 1) and WIS(i − 2)

252. How efficient is the recursive algorithm?
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
so WIS(i) makes recursive calls to WIS(i − 1) and WIS(i − 2)
6
WIS(6)

253. How efficient is the recursive algorithm?
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
so WIS(i) makes recursive calls to WIS(i − 1) and WIS(i − 2)
6
WIS(6)
5 4

254. How efficient is the recursive algorithm?
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
so WIS(i) makes recursive calls to WIS(i − 1) and WIS(i − 2)
6
WIS(6)
5 4
3 23
334

255. How efficient is the recursive algorithm?
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
so WIS(i) makes recursive calls to WIS(i − 1) and WIS(i − 2)
6
WIS(6)
5 4
3 2
02 1 1
3
3
2 1
34
3 23

256. How efficient is the recursive algorithm?
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
so WIS(i) makes recursive calls to WIS(i − 1) and WIS(i − 2)
6
WIS(6)
5 4
3 2
02
1 0
1
0 0
1
0 0
3
3
2
1 0
1
0 0
34
3 2
02 1 1
3

257. How efficient is the recursive algorithm?
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
so WIS(i) makes recursive calls to WIS(i − 1) and WIS(i − 2)
6
WIS(6)
5 4
3 2
02
1 0
0 0
1
0 0
1
0 0
3
3
2
1 0
0 0
1
0 0
34
3 2
02
1 0
1
0 0
1
0 0
3

258. How efficient is the recursive algorithm?
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
so WIS(i) makes recursive calls to WIS(i − 1) and WIS(i − 2)
6
WIS(6)
5 4
3 2
02
1 0
0 0
1
0 0
1
0 0
3
3
2
1 0
0 0
1
0 0
34
3 2
02
1 0
0 0
1
0 0
1
0 0
3

259. How efficient is the recursive algorithm?
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
so WIS(i) makes recursive calls to WIS(i − 1) and WIS(i − 2)
6
WIS(6)
5 4
3 2
02
1 0
0 0
1
0 0
1
0 0
3
3
2
1 0
0 0
1
0 0
34
3 2
02
1 0
0 0
1
0 0
1
0 0
3
This doesn’t look good (but it does look familiar)

260. How efficient is the recursive algorithm?
1
1
1
1
1
1
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
if we extend this input in the same way. . .

261. How efficient is the recursive algorithm?
1
1
1
1
1
1
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
if we extend this input in the same way. . .
1

262. How efficient is the recursive algorithm?
1
1
1
1
1
1
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
if we extend this input in the same way. . .
1
1

263. How efficient is the recursive algorithm?
1
1
1
1
1
1
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
if we extend this input in the same way. . .
1
1
1

264. How efficient is the recursive algorithm?
1
1
1
1
1
1
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
if we extend this input in the same way. . .
1
1
1

265. How efficient is the recursive algorithm?
1
1
1
1
1
1
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
if we extend this input in the same way. . .
1
1
1
Given n intervals set out in this manner,

266. How efficient is the recursive algorithm?
1
1
1
1
1
1
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
if we extend this input in the same way. . .
1
1
1
Given n intervals set out in this manner,
WIS(n) runs in exponential time

267. How efficient is the recursive algorithm?
1
1
1
1
1
1
If (i = 0)
Return 0
Return max WIS(i − 1), WIS(p(i)) + wi
WIS(i)
if we extend this input in the same way. . .
1
1
1
Given n intervals set out in this manner,
WIS(n) runs in exponential time
If T(n) is the run time of WIS(n) using these intervals
then T(n) > 2T(n − 2)

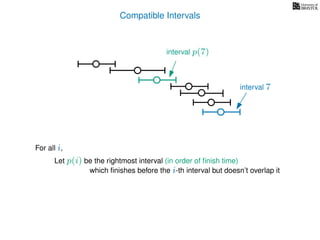
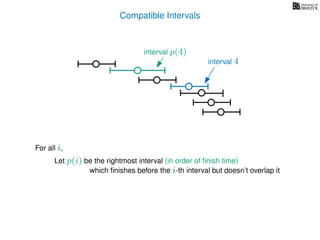
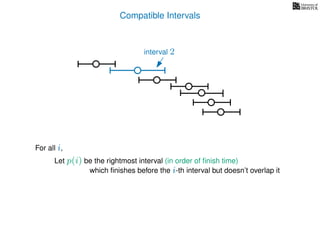
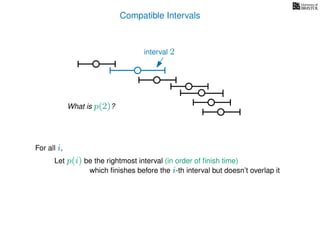
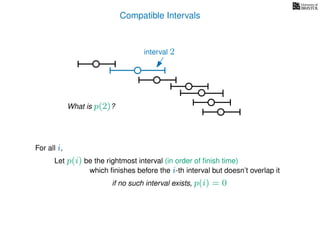
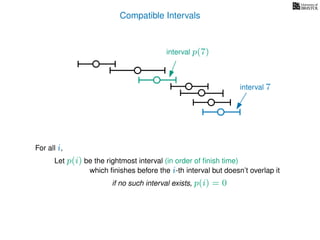
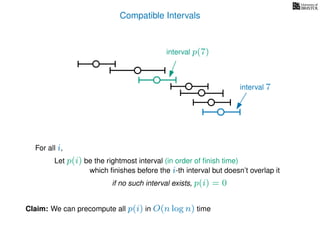
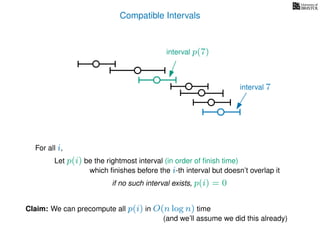
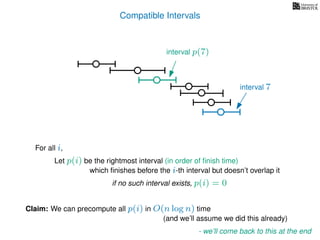
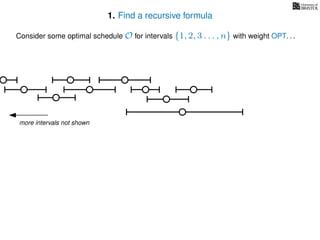
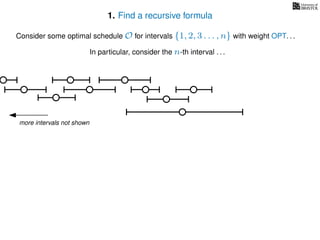
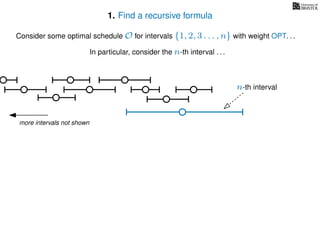
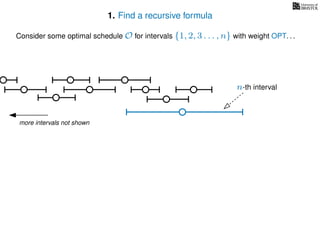
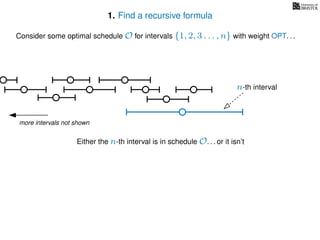
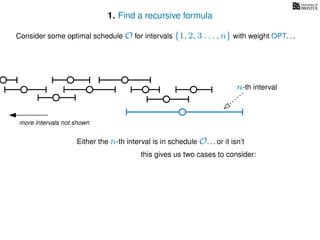
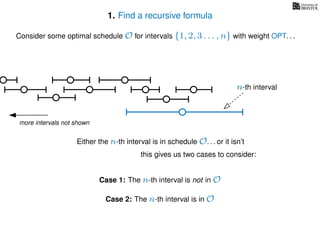
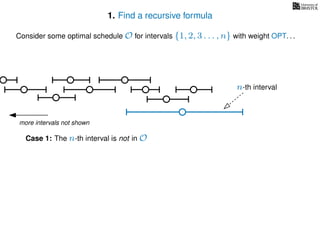
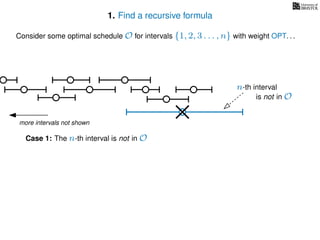
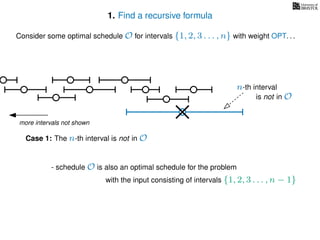
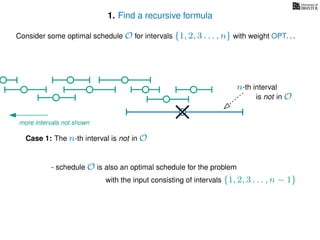
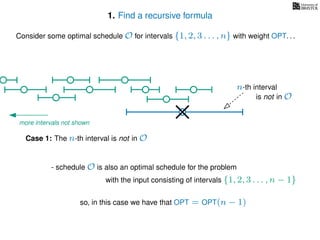
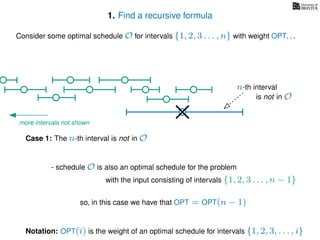
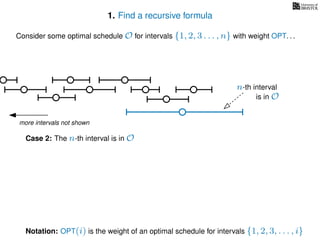
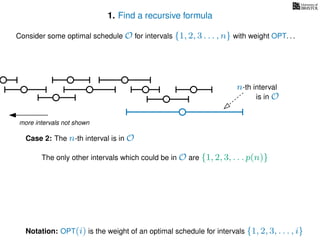
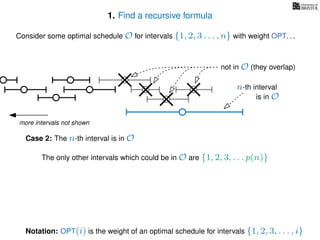
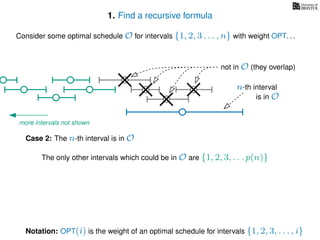
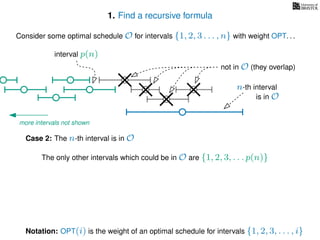
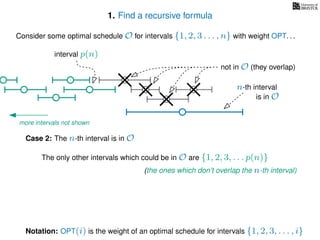
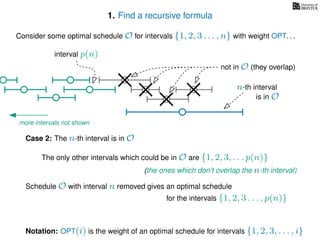
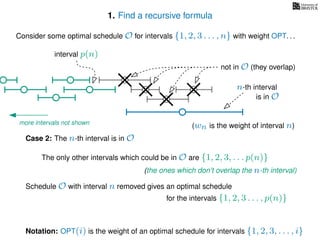
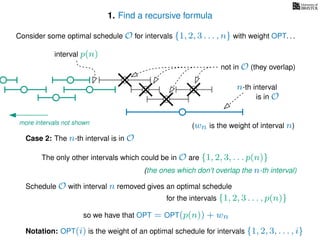
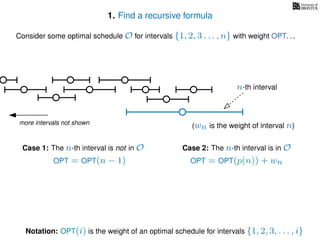
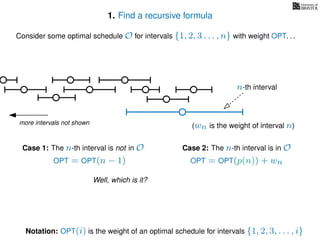
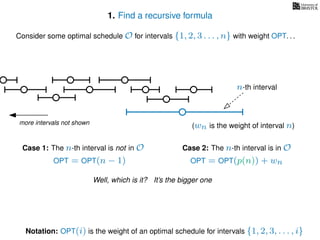
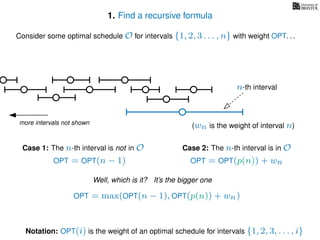
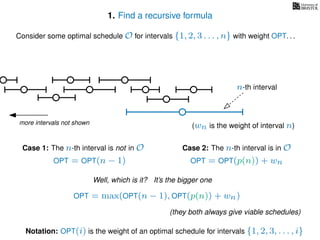
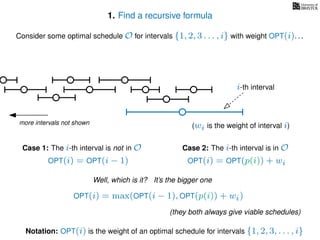
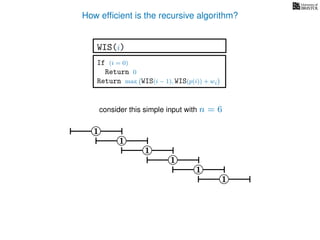
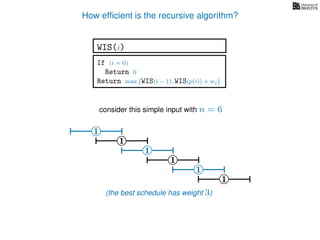
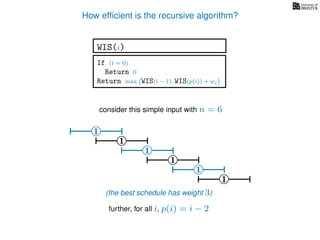
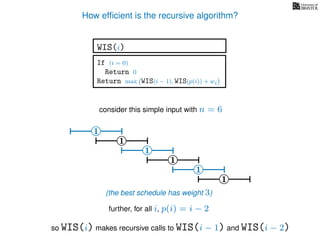
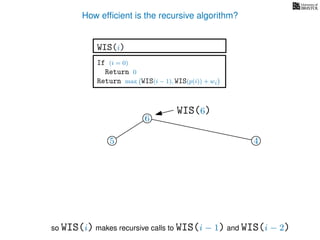
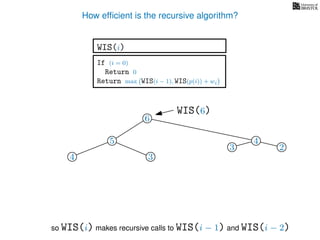
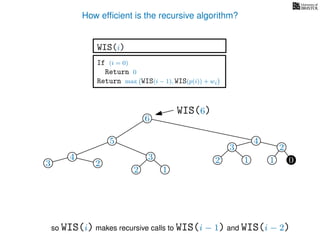
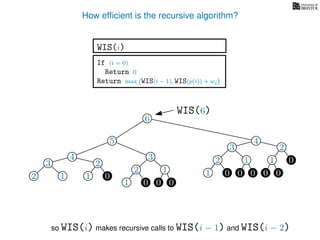
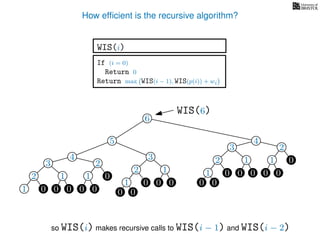
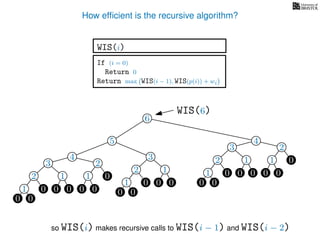
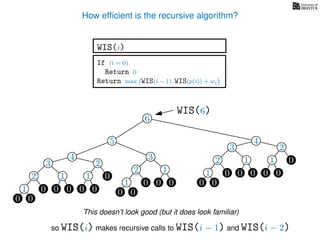
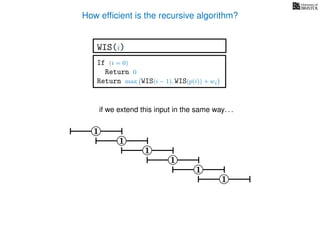
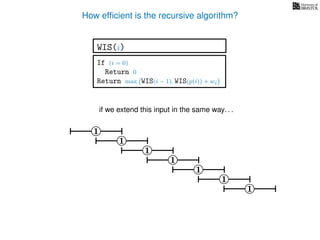
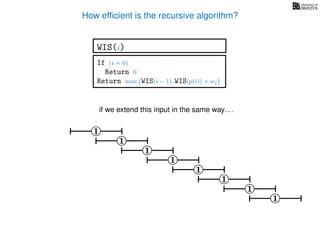
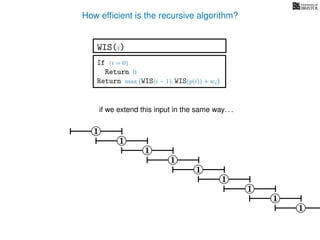
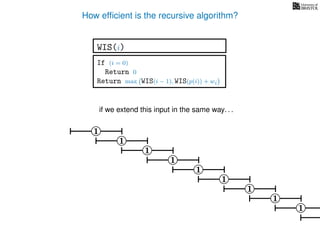
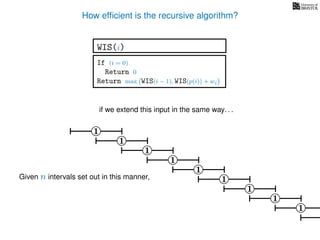
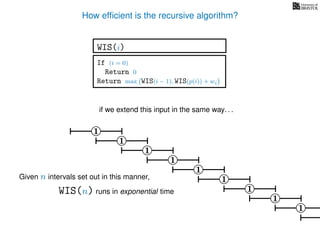
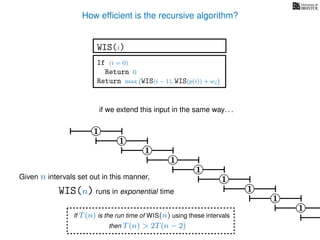
268. 3. Store the solutions to subproblems
If (i = 0)
Return 0
If WIS[i] undefined
WIS[i]= max MemWIS(i − 1), MemWIS(p(i)) + wi
Return WIS[i]
MemWIS(i)

269. 3. Store the solutions to subproblems
In the MemWIS version of the algorithm
we store solutions to previously computed subproblems
in an n length array called WIS
If (i = 0)
Return 0
If WIS[i] undefined
WIS[i]= max MemWIS(i − 1), MemWIS(p(i)) + wi
Return WIS[i]
MemWIS(i)

270. 3. Store the solutions to subproblems
(we have memoized the algorithm)
In the MemWIS version of the algorithm
we store solutions to previously computed subproblems
in an n length array called WIS
If (i = 0)
Return 0
If WIS[i] undefined
WIS[i]= max MemWIS(i − 1), MemWIS(p(i)) + wi
Return WIS[i]
MemWIS(i)

271. 3. Store the solutions to subproblems
(we have memoized the algorithm)
In the MemWIS version of the algorithm
we store solutions to previously computed subproblems
in an n length array called WIS
Each entry WIS[i] is only computed once
If (i = 0)
Return 0
If WIS[i] undefined
WIS[i]= max MemWIS(i − 1), MemWIS(p(i)) + wi
Return WIS[i]
MemWIS(i)

272. 3. Store the solutions to subproblems
(we have memoized the algorithm)
In the MemWIS version of the algorithm
we store solutions to previously computed subproblems
in an n length array called WIS
Each entry WIS[i] is only computed once
The time complexity of computing MemWIS(n) is now O(n)
If (i = 0)
Return 0
If WIS[i] undefined
WIS[i]= max MemWIS(i − 1), MemWIS(p(i)) + wi
Return WIS[i]
MemWIS(i)

273. 3. Store the solutions to subproblems
(we have memoized the algorithm)
In the MemWIS version of the algorithm
we store solutions to previously computed subproblems
in an n length array called WIS
Each entry WIS[i] is only computed once
The time complexity of computing MemWIS(n) is now O(n)
If (i = 0)
Return 0
If WIS[i] undefined
WIS[i]= max MemWIS(i − 1), MemWIS(p(i)) + wi
Return WIS[i]
MemWIS(i)
because every recursion causes an unfilled entry to be filled in the array

274. The dependency graph
What information do we need to compute WIS[i]?
The array
WIS:

275. The dependency graph
What information do we need to compute WIS[i]?
The array
WIS:
WIS[i]

276. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need

277. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]

278. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]

279. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]

280. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)

281. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)

282. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .

283. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm

284. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm
Fill in the array from
the left again

285. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm
Fill in the array from
the left again

286. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm
Fill in the array from
the left again

287. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm
Fill in the array from
the left again

288. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm
Fill in the array from
the left again

289. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm
Fill in the array from
the left again

290. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm
Fill in the array from
the left again

291. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm
Fill in the array from
the left again

292. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm
Fill in the array from
the left again

293. The dependency graph
What information do we need to compute WIS[i]?
to compute
The array
WIS:
WIS[i − 1] and WIS[p(i)]
WIS[i]
WIS[i] we need
WIS[i − 1]
WIS[p(i)]
both of which are to the left of WIS[i]
(somewhere)
all of the dependencies go left. . .
This suggests another
iterative algorithm
Fill in the array from
the left again

294. 4. Derive an iterative algorithm
This is an iterative dynamic programming algorithm
it runs in O(n) time
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]
for Weighted Interval Scheduling

295. 4. Derive an iterative algorithm
This is an iterative dynamic programming algorithm
it runs in O(n) time
. . . but it requires than you precomputed all the p(i) values
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]
for Weighted Interval Scheduling

296. How do you find all those p(i) values?
Revised Claim: We can precompute any p(i) in O(log n) time
interval p(7)
interval 7

297. How do you find all those p(i) values?
Revised Claim: We can precompute any p(i) in O(log n) time
interval p(7)
interval 7
Recall that si is the start time of interval i
and fi is the finish time of interval i

298. How do you find all those p(i) values?
Revised Claim: We can precompute any p(i) in O(log n) time
interval p(7)
interval 7
Recall that si is the start time of interval i
We want to find the unique value j = p(i) such that
and fi is the finish time of interval i
fj < si < fj+1.

299. How do you find all those p(i) values?
Revised Claim: We can precompute any p(i) in O(log n) time
interval p(7)
interval 7
Recall that si is the start time of interval i
We want to find the unique value j = p(i) such that
and fi is the finish time of interval i
fj < si < fj+1.
si
f1 f2 f3 f4 f5f6 f7

300. How do you find all those p(i) values?
Revised Claim: We can precompute any p(i) in O(log n) time
interval p(7)
interval 7
Recall that si is the start time of interval i
We want to find the unique value j = p(i) such that
and fi is the finish time of interval i
fj < si < fj+1.
As the input is sorted by finish times, we can find j by binary search in O(log n) time
si
f1 f2 f3 f4 f5f6 f7

301. How do you find all those p(i) values?
Revised Claim: We can precompute any p(i) in O(log n) time
interval p(7)
interval 7

302. How do you find all those p(i) values?
Revised Claim: We can precompute any p(i) in O(log n) time
interval p(7)
interval 7
Original Claim: We can precompute all p(i) in O(n log n) time

303. How do you find all those p(i) values?
Revised Claim: We can precompute any p(i) in O(log n) time
interval p(7)
interval 7
Original Claim: We can precompute all p(i) in O(n log n) time
(by using the revised claim n times)

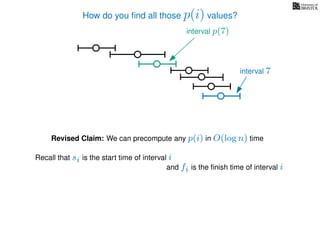
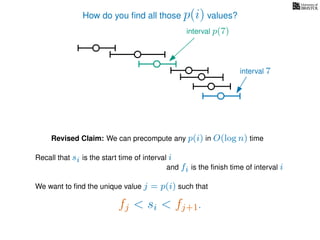
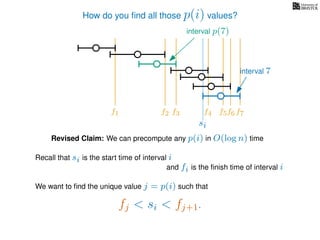
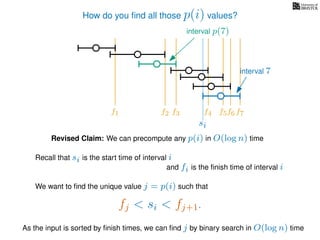
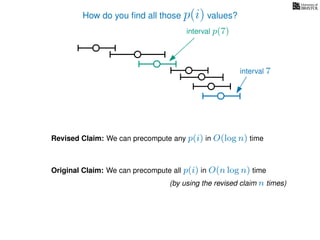
304. Wait, did you want the actual schedule?
but doesn’t find the actual schedule
ItWIS(n) finds the weight of the optimal schedule
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]

305. Wait, did you want the actual schedule?
but doesn’t find the actual schedule
There is an optimal schedule for {1, 2, . . . , i} containing
interval i if and only if
WIS[i − 1] WIS[p(i)]+wi
ItWIS(n) finds the weight of the optimal schedule
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]

306. Wait, did you want the actual schedule?
but doesn’t find the actual schedule
There is an optimal schedule for {1, 2, . . . , i} containing
interval i if and only if
WIS[i − 1] WIS[p(i)]+wi
(by the argument we saw earlier)
ItWIS(n) finds the weight of the optimal schedule
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]

307. Wait, did you want the actual schedule?
There is an optimal schedule for {1, 2, . . . , i} containing
interval i if and only if
WIS[i − 1] WIS[p(i)]+wi
(by the argument we saw earlier)
ItWIS(n) finds the weight of the optimal schedule
and FINDWIS(n) finds the actual schedule
FindWIS(i)
If (i = 0)
Return nothing
If WIS[i − 1] WIS[p(i)]+wi
Return FindWIS(p(i)) then i
Return FindWIS(i − 1)
This is called backtracking and works for lots of Dynamic Programming algorithms
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]

308. Wait, did you want the actual schedule?
There is an optimal schedule for {1, 2, . . . , i} containing
interval i if and only if
WIS[i − 1] WIS[p(i)]+wi
(by the argument we saw earlier)
ItWIS(n) finds the weight of the optimal schedule
and FINDWIS(n) finds the actual schedule
FindWIS(i)
If (i = 0)
Return nothing
If WIS[i − 1] WIS[p(i)]+wi
Return FindWIS(p(i)) then i
Return FindWIS(i − 1)
This is called backtracking and works for lots of Dynamic Programming algorithms
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]

309. The final algorithm
ItWIS(n) finds the weight of the optimal schedule
and FINDWIS(n) finds the actual schedule
The final algorithm:
Step 1: Find all the p(i) values
Step 2: Run ItWIS(n) to find the optimal weight
Step 3: Run FindWIS(n) to find the schedule
FindWIS(i)
If (i = 0)
Return nothing
If WIS[i − 1] WIS[p(i)]+wi
Return FindWIS(p(i)) then i
Return FindWIS(i − 1)
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]

310. The final algorithm
ItWIS(n) finds the weight of the optimal schedule
and FINDWIS(n) finds the actual schedule
The final algorithm:
Step 1: Find all the p(i) values
Step 2: Run ItWIS(n) to find the optimal weight
Step 3: Run FindWIS(n) to find the schedule
O(n log n) time
FindWIS(i)
If (i = 0)
Return nothing
If WIS[i − 1] WIS[p(i)]+wi
Return FindWIS(p(i)) then i
Return FindWIS(i − 1)
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]

311. The final algorithm
ItWIS(n) finds the weight of the optimal schedule
and FINDWIS(n) finds the actual schedule
The final algorithm:
Step 1: Find all the p(i) values
Step 2: Run ItWIS(n) to find the optimal weight
Step 3: Run FindWIS(n) to find the schedule
O(n log n) time
O(n) time
FindWIS(i)
If (i = 0)
Return nothing
If WIS[i − 1] WIS[p(i)]+wi
Return FindWIS(p(i)) then i
Return FindWIS(i − 1)
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]

312. The final algorithm
ItWIS(n) finds the weight of the optimal schedule
and FINDWIS(n) finds the actual schedule
The final algorithm:
Step 1: Find all the p(i) values
Step 2: Run ItWIS(n) to find the optimal weight
Step 3: Run FindWIS(n) to find the schedule
O(n log n) time
O(n) time
O(n) time
FindWIS(i)
If (i = 0)
Return nothing
If WIS[i − 1] WIS[p(i)]+wi
Return FindWIS(p(i)) then i
Return FindWIS(i − 1)
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]

313. The final algorithm
ItWIS(n) finds the weight of the optimal schedule
and FINDWIS(n) finds the actual schedule
The final algorithm:
Step 1: Find all the p(i) values
Step 2: Run ItWIS(n) to find the optimal weight
Step 3: Run FindWIS(n) to find the schedule
O(n log n) time
O(n) time
O(n) time
Overall this takes O(n log n) time
FindWIS(i)
If (i = 0)
Return nothing
If WIS[i − 1] WIS[p(i)]+wi
Return FindWIS(p(i)) then i
Return FindWIS(i − 1)
ItWIS(n)
If (i = 0)
Return 0
For i = 1 to n
WIS[i]= max WIS[i − 1],WIS[p(i)]+wi
Return WIS[i]

314. Introduction
Dynamic programming is recursion without repetition
Dynamic programming is a technique for finding efficient algorithms for problems which
can be broken down into simpler, overlapping subproblems.
in other words. . .
The basic idea:
1. Find a recursive formula for the problem
(typically this is the hard bit)
3. Speed it up by storing the solutions to subproblems (memoization)
(to avoid recomputing the same thing over and over)
4. Derive an iterative algorithm by solving the subproblems in a good order
(iterative algorithms are often better in practice, easier to analyse and prettier)
- in terms of answers to subproblems.
2. Write down a naive recursive algorithm
(typically this algorithm will take exponential time)
Summary
Introduction
Summary