The document discusses various algorithms and principles related to randomized algorithms, specifically focusing on the Lovász local lemma and modern Erdős magic, which deals with the existence of satisfying assignments in k-SAT problems. It explores Moser's fix-it algorithm, which offers a method for finding satisfactory assignments through a series of random assignments and adjustments. Additionally, the document touches on conjectures and theorems regarding the identification of outliers within sets, emphasizing the limits of polynomial time solutions.

1. Finding Needles in Exponential Haystacks
Joel Spencer
June 6, 2014
Yandex - Moscow

2. Erd˝os Magic:
If a random object has a positive probability of being
good than a good object MUST exist

3. Modern Erd˝os Magic:
If a randomized algorithm has a positive probability of
producing a good object than a good object MUST exist

4. Working with Paul Erd˝os was like taking a walk in the hills. Every
time when I thought that we had achieved our goal and deserved a
rest, Paul pointed to the top of another hill and off we would go.
– Fan Chung

5. PART I
The Lov´asz Local Lemma

6. k-SAT
Boolean x1, . . . , xn. ys is xs or xs
Clause C = yi1 ∨ . . . ∨ yik
k-SAT instance: ∧α∈I Cα
Cα, Cβ overlap if common xj .
Assume: Each Cα overlaps ≤ d Cβ
Assume: ed2−k ≤ 1
LLL: Then satisfiable.

7. k-SAT
Fix d, k (e.g.: k = 5, d = 10) but let n → ∞
Where is the satisfying assignment?
Original Proof: Can’t Find it

8. k-SAT
Fix d, k (e.g.: k = 5, d = 10) but let n → ∞
Where is the satisfying assignment?
Original Proof: Can’t Find it
MOSER: I can find it!

9. FIX-IT!
Moser’s FIX-IT Algorithm
FIX-IT I Randomly assign xj ← {t, f }

10. FIX-IT!
Moser’s FIX-IT Algorithm
FIX-IT I Randomly assign xj ← {t, f }
FIX-IT II WHILE some clause Cα ← f

11. FIX-IT!
Moser’s FIX-IT Algorithm
FIX-IT I Randomly assign xj ← {t, f }
FIX-IT II WHILE some clause Cα ← f
FIX-IT IIIa Select one bad clause Cα

12. FIX-IT!
Moser’s FIX-IT Algorithm
FIX-IT I Randomly assign xj ← {t, f }
FIX-IT II WHILE some clause Cα ← f
FIX-IT IIIa Select one bad clause Cα
FIX-IT IIIb Randomly Reassign xj ← {t, f } for all xj in Cα

13. FIX-IT!
Moser’s FIX-IT Algorithm
FIX-IT I Randomly assign xj ← {t, f }
FIX-IT II WHILE some clause Cα ← f
FIX-IT IIIa Select one bad clause Cα
FIX-IT IIIb Randomly Reassign xj ← {t, f } for all xj in Cα
FIX-IT IV

14. FIX-IT!
Moser’s FIX-IT Algorithm
FIX-IT I Randomly assign xj ← {t, f }
FIX-IT II WHILE some clause Cα ← f
FIX-IT IIIa Select one bad clause Cα
FIX-IT IIIb Randomly Reassign xj ← {t, f } for all xj in Cα
FIX-IT IV There is no IV!

15. The LOG
LOG - Clauses reassigned in order FIX-IT IIIb applies
TLOG = length of LOG. (= ∞ if no stop)
Modern Erd˝os Magic: E[TLOG] < ∞ implies satisfiable and a
good 1 algorithm
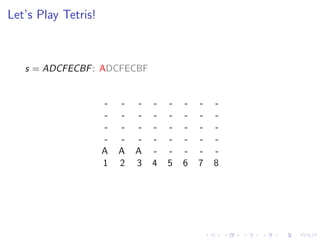
Example: Variables 12345678. Clauses A : 123, B : 234, C : 345,
D : 456, E : 567, F : 678. LOG = ADCFECBF
1
with E[TLOG] reasonable

16. Let’s Play Tetris!
s = ADCFECBF: ADCFECBF
- - - - - - - -
- - - - - - - -
- - - - - - - -
- - - - - - - -
A A A - - - - -
1 2 3 4 5 6 7 8

17. Let’s Play Tetris!
s = ADCFECBF: ADCFECBF
- - - - - - - -
- - - - - - - -
- - - - - - - -
- - - - - - - -
A A A D D D - -
1 2 3 4 5 6 7 8

18. Let’s Play Tetris!
s = ADCFECBF: ADCFECBF
- - - - - - - -
- - - - - - - -
- - - - - - - -
- - C C C - - -
A A A D D D - -
1 2 3 4 5 6 7 8

19. Let’s Play Tetris!
s = ADCFECBF: ADCFECBF
- - - - - - - -
- - - - - - - -
- - - - - - - -
- - C C C F F F
A A A D D D - -
1 2 3 4 5 6 7 8

20. Let’s Play Tetris!
s = ADCFECBF: ADCFECBF
- - - - - - - -
- - - - - - - -
- - - - E E E -
- - C C C F F F
A A A D D D - -
1 2 3 4 5 6 7 8

21. Let’s Play Tetris!
s = ADCFECBF: ADCFECBF
- - - - - - - -
- - C C C - - -
- - - - E E E -
- - C C C F F F
A A A D D D - -
1 2 3 4 5 6 7 8

22. Let’s Play Tetris!
s = ADCFECBF: ADCFECBF
- B B B - - - -
- - C C C - - -
- - - - E E E -
- - C C C F F F
A A A D D D - -
1 2 3 4 5 6 7 8

23. Let’s Play Tetris!
s = ADCFECBF: ADCFECBF
- B B B - - - -
- - C C C F F F
- - - - E E E -
- - C C C F F F
A A A D D D - -
1 2 3 4 5 6 7 8

24. Let’s Play Tetris!
s = ADCFECBF
- B B B - - - -
- - C C C F F F
- - - - E E E -
- - C C C F F F
A A A D D D - -
1 2 3 4 5 6 7 8
The Pyramid Pyr(s) = ADCFEF is support of last:
- - - - - F F F
- - - - E E E -
- - C C C F F F
A A A D D D - -
1 2 3 4 5 6 7 8

25. Analysis
Pyramids of prefixes of LOG distinct.
ADCFECBF: A; D; ADC;
DF;ADCFE;ADCFEC;ADCFECB;ADCFEF
E[TLOG] = s Pr[s pyramid of prefix ]

26. Preprocess Randomness
Each xj chooses countably many assignments.
Probability X1 · · · Xt is pyramid of prefix is ≤ (2−k )t
- - C C C - - -
A A A - - - - -
1 2 3 4 5 6 7 8
A, C false with different coinflips!

27. An Interesting Algebra
X, Y commute if no overlap.
Tetris same if and only if equal in algebra
ADC = DAC
- - C C C - - -
A A A D D D - -
1 2 3 4 5 6 7 8
ADC, DAC use same coinflips.

28. Algebraic Combinatorics
Property KNUTH: s(2−k )length(s) < ∞
(sum over pyramids s in algebra)
E[TLOG] ≤ s(2−k )length(s)
Modern Erd˝os Magic: [KNUTH] implies satisfiability and FIX-IT
takes “time” at most sum.
Algebraic Combinatorics: When does [KNUTH] hold?
Partial Answer: if ed2−k ≤ 1

29. A Prescient Adversary
FIX-IT I Randomly assign xj ← {t, f }
FIX-IT II WHILE some clause Cα ← f
FIX-IT IIIa Select one bad clause Cα
FIX-IT IIIb Randomly Reassign xj ← {t, f } for all xj in Cα
Each xj selects countably many t, f .
Adversary knows coinflips in advance
Still can’t stop FIX-IT from halting!

30. PART II
Eliminating Outliers

31. Six Standard Deviations Suffice
S1, . . . , Sn ⊆ {1, . . . , n}
χ : {1, . . . , n} → {−1 + 1} = {red, blue}
χ(S) := j∈S χ(j), disc(S) = |χ(S)| = |red − blue|
Theorem (JS/1985): There exists χ
disc(Si) ≤ 6
√
n for all 1 ≤ i ≤ n

32. Six Standard Deviations Suffice
S1, . . . , Sn ⊆ {1, . . . , n}
χ : {1, . . . , n} → {−1 + 1} = {red, blue}
χ(S) := j∈S χ(j), disc(S) = |χ(S)| = |red − blue|
Theorem (JS/1985): There exists χ
disc(Si) ≤ 6
√
n for all 1 ≤ i ≤ n
Conjecture (JS/1986-2009) You can’t find χ in polynomial time.

33. Six Standard Deviations Suffice
S1, . . . , Sn ⊆ {1, . . . , n}
χ : {1, . . . , n} → {−1 + 1} = {red, blue}
χ(S) := j∈S χ(j), disc(S) = |χ(S)| = |red − blue|
Theorem (JS/1985): There exists χ
disc(Si) ≤ 6
√
n for all 1 ≤ i ≤ n
Conjecture (JS/1986-2009) You can’t find χ in polynomial time.
Theorem (Bansal/2010): Yes I can!

34. Six Standard Deviations Suffice
S1, . . . , Sn ⊆ {1, . . . , n}
χ : {1, . . . , n} → {−1 + 1} = {red, blue}
χ(S) := j∈S χ(j), disc(S) = |χ(S)| = |red − blue|
Theorem (JS/1985): There exists χ
disc(Si) ≤ 6
√
n for all 1 ≤ i ≤ n
Conjecture (JS/1986-2009) You can’t find χ in polynomial time.
Theorem (Bansal/2010): Yes I can!
Theorem (Lovett, Meka/2012): We can too!

35. A Vector Formulation
ri ∈ Rn, 1 ≤ i ≤ n, |ri |∞ ≤ 1
Initial z ∈ [−1, +1]n (e.g.: z = 0.)
Theorem: There exists x ∈ {−1, +1}n with
|ri · (x − z)| ≤ K
√
n
for all 1 ≤ i ≤ n.

36. A Vector Formulation
ri ∈ Rn, 1 ≤ i ≤ n, |ri |∞ ≤ 1
Initial z ∈ [−1, +1]n (e.g.: z = 0.)
Theorem: There exists x ∈ {−1, +1}n with
|ri · (x − z)| ≤ K
√
n
for all 1 ≤ i ≤ n.
z = 0, x random. Problem: OUTLIERS!

37. Phase I
Find x ∈ [−1, +1]n with all least n
2 at ±1.
Idea: Start x ← z. Move x in a Controlled Brownian Motion.

38. Phase I
Find x ∈ [−1, +1]n with all least n
2 at ±1.
Idea: Start x ← z. Move x in a Controlled Brownian Motion.
Technical: i frozen if |xi | ≥ 1 − ǫ. Each step of distance δ

39. Phase I
Find x ∈ [−1, +1]n with all least n
2 at ±1.
Idea: Start x ← z. Move x in a Controlled Brownian Motion.
Technical: i frozen if |xi | ≥ 1 − ǫ. Each step of distance δ
Set Lj = [n−1/2rj ] · [x − z]
WANT: ALL |Lj | ≤ K

40. Space V of allowable moves y = (y1, . . . , yn)

41. Space V of allowable moves y = (y1, . . . , yn)
i frozen ⇒ yi = 0.

42. Space V of allowable moves y = (y1, . . . , yn)
i frozen ⇒ yi = 0.
y orthogonal to current x

43. Space V of allowable moves y = (y1, . . . , yn)
i frozen ⇒ yi = 0.
y orthogonal to current x
KEY: y orthogonal to rj for j with top n
4 |Lj |

44. The Random Move
d = dim(V ) ≥ n
4 − 1 ∼ n
4 .
Gaussian g = d−1/2[n1b1 + . . . + nd bd ], orthonormal bs
Move x ← x + δg

45. The Random Move
d = dim(V ) ≥ n
4 − 1 ∼ n
4 .
Gaussian g = d−1/2[n1b1 + . . . + nd bd ], orthonormal bs
Move x ← x + δg
Lj ← Lj + δ[n−1/2rj ] · g
Gaussian Nondirectional
Lj ← Lj + N(0, τ2) with τ2 ≤ 1
d δ2 ≤ 4
n δ2

46. Gaussian Casino
Martingale 0 = X0, X1, . . . , XT .
∆t = Xt − Xt−1 ∼ N(0, τ2) with τ2 ≤ σ2
t
σ2 := σ2
1 + . . . + σ2
T
Theorem: Pr[XT ≥ λσ] ≤ exp[−λ2/2]
Theorem: Pr[max0≤t≤T Xt ≥ λσ] ≤ exp[−λ2/2]

47. |x|2 ← |x|2 + δ2. Set T = 4nδ−2 (fictitious continuation).
Fix j. Xt value of Lj after step t.
Martingale!
σ2 = T · 4
n δ2 = 16
Pr[|Lj | ≥ K] ≤ 2e−K2/32 ≤ 0.1
Pr[|Lj | ≥ K at any time ] ≤ 0.1.
SUCCESS: Fewer than n
5 j with |Lj | ≥ K.
Positive Probability of SUCCESS

48. |x|2 ← |x|2 + δ2. Set T = 4nδ−2 (fictitious continuation).
Fix j. Xt value of Lj after step t.
Martingale!
σ2 = T · 4
n δ2 = 16
Pr[|Lj | ≥ K] ≤ 2e−K2/32 ≤ 0.1
Pr[|Lj | ≥ K at any time ] ≤ 0.1.
SUCCESS: Fewer than n
5 j with |Lj | ≥ K.
Positive Probability of SUCCESS
SUCCESS implies that ALL |Lj | ≤ K

49. Phase s
m = 21−s n. Start z with ≤ m coordinates frozen. End x with ≤ m
2
coordinates frozen.
Effectively |rj | ≤
√
m
Would get K
√
m but still have n = m2s−1 vectors.
Actually get: K
√
m
√
s = K
√
n
√
s2(1−s)/2
Converges!

50. Thank You!
It is six in the morning.
The house is asleep.
Nice music is playing.
I prove and conjecture.
– Paul Erd˝os, in letter to Vera S´os