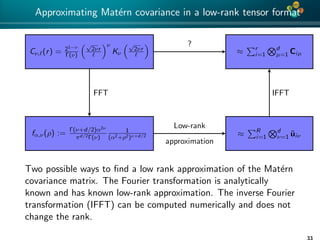
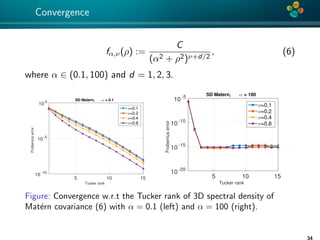
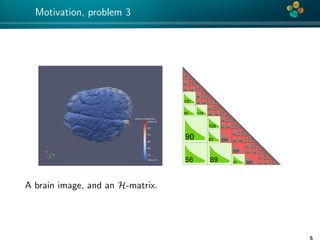
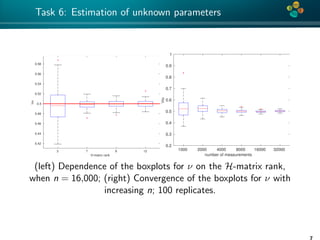
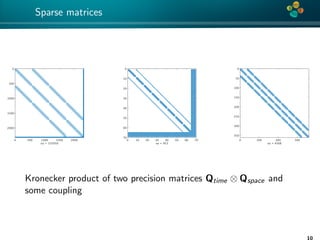
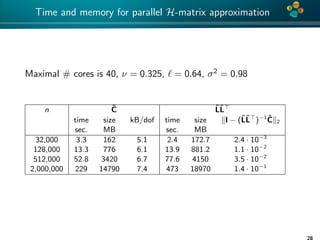
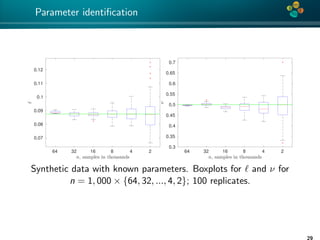
The document presents an overview of low-rank and sparse techniques in spatial statistics and parameter identification, highlighting their applications in predicting environmental variables. It addresses key problems such as predicting temperature and salinity, improving statistical models for moisture, and estimating covariance parameters. The document also outlines various statistical tasks and the techniques available, including sparse matrices and low-rank methods.

1. Overview of Low-rank and Sparse Techniques in
Spatial Statistics and Parameter Identification
Alexander Litvinenko
Bayesian Computational Statistics & Modeling, KAUST
https://bayescomp.kaust.edu.sa/
KAUST Biostatistics Group Seminar,
October 3, 2018

2. 4*
The structure of the talk
We collect a lot of data, it is easy and cheap nowdays.
Major Goal: Develop new statistical tools to address new problems.
1. Low-rank matrices
2. Sparse matrices
3. Hierarchical matrices
4. Approximation of Mat´ern covariance functions and joint
Gaussian likelihoods
5. Identification of unknown parameters via maximizing Gaussian
log-likelihood
6. Low-rank tensor methods
2

3. 4*
Motivation, problem 1
Task: to predict temperature, velocity, salinity, estimate parameters of
covariance
Grid: 50Mi locations on 50 levels, 4*(X*Y*Z) + X*Y= 4*500*500*50 +
500*500 = 50Mi.
High-resolution time-dependent data about Red Sea: zonal velocity and
temperature
3

4. 4*
Motivation, problem 2
Tasks: 1) to improve statistical model, which predicts moisture; 2) use
this improved model to forecast missing values.
Given: n ≈ 2.5Mi observations of moisture data
−120 −110 −100 −90 −80 −70
253035404550
Soil moisture
longitude
latitude
0.15
0.20
0.25
0.30
0.35
0.40
0.45
0.50
High-resolution daily soil moisture data at the top layer of the Mississippi
basin, U.S.A., 01.01.2014 (Chaney et al., in review).
Important for agriculture, defense, ...
4

5. 4*
Motivation, problem 3
3
2
4 2
9
2
4 2
17
2
2
4 2
7 3 2
18 17
10 10
2
5 2
8
2
4 2
10 3 3 2
32
14 10
18 10
36 28
3
6
2
4 2
14
2
4 2
5 2
4 2
14 18
14 18
2
4 2
8
2
5 3
19
2
4 2
6 3
6 3
65
32
19 21
18 18
29 29
61 61
2
5 3
7 3 2
5 2
18
3
6 3
6 3
17 17
12 12
3 2
7
2
4 2
2
12 3
2
4 2
32
17 12
12 12
29 29
2
5
3 2
7
2
4 2
12
2
5 3
10 10
19 12
3 3 2
10
2
5 2
5 2
4 2
119
65
32
10 15
10 19
27 27
54 54
118 118
2
5
3
4 2
15
2
5 3
11
3
6 3
15 17
10 10
2
4 2
8
2
4 2
10
3 2
3
21
14 10
7 7
33 27
2
4 3 3 2
7 3
8 7
14 7
2
3
8
2
4 2
7 3 2
10
2
5 2
59
21
8 18
8 12
21 29
59 54
3
6 3 2
5 2
12
2
5 3 2
18 12
11 11
3 2
7
3
5 2
11
2
5 3
25
9 9
16 11
30 29
3
3
9
3
4 2
6 3
9 16
9 16
3 2
4 2
7 3 2
16
3 2
7
2
4 2
121
119
59
25
18 16
10 10
25 34
59 59
119 118
80 119
2
4
2
4 2
9
2
4 2
10
3
4 2
19 10
15 10
2
5
3 2
7 3 2
15
3
4 2
5 2
31
15 15
16 15
32 34
3 2
4 2
4 2
15
2
4 3 2
5 2
15 16
15 16
2
5 3 2
12
3
6 3
20
3 2
7 3 2
6 3
58
27
18 18
9 9
31 31
66 67
2
5
3 2
6 3
9
2
4 2
12 9
18 9
3
6 3
12
3
4 2
9
2
4 2
27
12 16
12 19
27 31
3 2
3
6 3
16
2
5
2
4 2
6 3
16 20
8 8
2
4 2
7 3 2
7 3 2
8
2
3
115
58
30
15 8
15 8
28 28
57 57
119 119
2
5
2
4 2
2
15
2
4 2
6 3
9 9
15 15
3 3
9
2
5
3 2
7 3 2
27
9 16
9 11
30 28
3
5 2
5 2
11
2
5 2
16 11
13 11
3 3 2
7 3 2
13
2
5
2
4 2
48
25
5 5
17 13
23 23
58 57
2
5
2
4 2
5 2
6 3
5 8
5 15
2 3
8
3 2
2
6 3
25
8 15
8 9
25 23
2
5 3
6 3
7 3 2
9
2
4 2
15 9
23 9
3
3
6 3
15
2
4 2
5 2
10
2
5 2
90
122
115
48
32
15 15
15 17
33 33
48 60
115 119
81 234
56 89
3 2
7
2
4 2
15
3
4 2
7 3 2
15 17
6 6
2
5
2
5 3
11
2
5 3
6 3
30
11 6
19 6
30 30
3
5 2
11
3 2
7 3 2
5 2
11 13
11 17
2
4 2
5 2
13
3
5 2
6 3
65
30
13 17
13 17
30 30
61 60
2
4
3
6 3
5 2
21
2
4
2
4 2
12
3
6 3
20 20
14 14
2
4 2
8
2
4 2
3
14
2
5 2
4 2
32
17 14
15 14
29 29
2
4 2
8
2
4 2
15
2
5
2
5 2
10 10
17 15
2
5 2
10
3
6
2
4 2
5 2
125
75
32
10 18
10 19
32 29
69 61
125 134
2
5
3 2
6 3
18
3 2
6 3
8
2
4 2
17 17
18 19
2
4 2
8
2
4 2
17
3
6 3 2
6 3
39
17 19
17 18
25 25
3 2
7
2
4 2
11
2
4 3 2
18
3
6
3
6 3
10 10
15 15
3 2
3
10
2
4 3
5 2
65
30
10 15
10 12
35 25
69 69
2
4 2
9
2
4 2
12 2
2
5 2
18 12
14 12
2
5 2
10
2
4 3 2
14
3
6
2
4 2
30
15 14
16 14
30 35
2
4 2
6 3
15
3 2
4 2
5 2
15 15
15 16
2
4 2
5 2
2
15
3
6 3
8
2
4 2
3
227
111
61
31
15 21
15 16
24 24
50 50
116 116
81 224
3
6 3
9
2
4 2
16
2
5 2
6 2
19 16
5 5
2
5 3
8
2
4 2
5 2
23
16 5
7 5
27 24
3
6
2
5 2
7
2
3
10 7
16 7
3
4 2
10
3
6
3
5 2
54
23
10 17
10 11
23 25
61 50
2
2
7
2
5 3
11
2
5 2
13 11
12 11
3
2
5 2
12
2
4
2
4 2
29
13 12
13 12
27 25
2
5
2
5 2
15
2
5
3 2
7
2
4 2
15 18
9 9
2
5 2
5 2
3
9
2
4 2
111
54
33
18 9
12 9
22 22
54 59
110 110
3 2
7
2
4 2
6 3
12
2
5 3 2
9 9
13 12
2
4 2
9
3 2
6 3
33
9 13
9 13
22 22
3 2
6 3
9
2
4 2
15
2
4 2
6 3
12 12
10 10
2
2
6 3
10
2
4 2
49
23
7 7
12 10
26 22
55 59
3
7
3
2
4 2
4 2
7 8
7 16
3 2
8
3
6 3
6 3
23
8 15
8 11
23 26
3
2
7 3 2
11
2
4 2
3
12 11
15 11
3 2
5 2
12
2
4 2
6 3
8
2
4 2
A brain image, and an H-matrix.
5

6. 4*
Five tasks in statistics to solve
Task 1. Approximate a Mat´ern covariance function in a low-rank
format.
Task 2. Computing Cholesky C = LLT or C1/2
Task 3. Kriging estimate ˆs = Csy C−1
yy y.
Task 4. Geostatistical design
φA = N−1
trace Css|y , and φC = zT
(Css|y )z,
where Css|y := Css − Csy C−1
yy Cys
Task 5. Computing the joint Gaussian log-likelihood function
L(θ) = −
N
2
log(2π) −
1
2
log det{C(θ)} −
1
2
(zT
· C(θ)−1
z).
6

7. 4*
Task 6: Estimation of unknown parameters
H-matrix rank
3 7 9 12
nu
0.42
0.44
0.46
0.48
0.5
0.52
0.54
0.56
0.58
number of measurements
1000 2000 4000 8000 16000 32000
nu
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
(left) Dependence of the boxplots for ν on the H-matrix rank,
when n = 16,000; (right) Convergence of the boxplots for ν with
increasing n; 100 replicates.
7

8. 4*
Which low-rank/sparse techniques are available ?
Sparse, low-rank, H-matrices, low-rank tensors, combination,...
8

9. 4*
Overview
1. sparse: storage O(n), many data formats, not easy
algorithms, 5-6 existing packages, limited applicability
2. low-rank: storage O(n), based on SVD, easy algorithms, a lot
of packages, limited applicability
3. H-matrices: O(knlogn), not trivial implementation, very wide
applicability
4. low-rank tensors: for d-dimensional problems (d > 3), many
formats, O(dnk), based on SVD/QR
5. combination of above:
9

10. 4*
Sparse matrices
Kronecker product of two precision matrices Qtime ⊗ Qspace and
some coupling
10

11. 4*
Low-rank (rank-k) matrices
M ∈ Rn×m, U ≈ U ∈ Rn×k, V ≈ V ∈ Rm×k, k min(n, m).
The storage M = UΣV T is k(n + m) instead of n · m for M
represented in the full matrix format.
VU Σ
T=M
U
VΣ∼
∼ ∼ T
=M
∼
Figure: Reduced SVD, only k biggest singular values are taken.
11

12. 4*
H-matrix approximations of C, L and C−1
43
13
28
14 34
10 5
9 15
44
13
29
13 35
14 7
5 14
50
14 62
15 6
6 15
60
15
31
17 44
13
14 6
7 14
3 13 6
5
16
12 8
7 15
3 15
34
11 31
16 59
13 6
7 12
58
15 51
16 7
6 16
31
15 39
12
36
14 40
15 6
6 17
32
14 40
10 7
7 10
41
16 35
5
13 8
6
9
10 7
7 9
3 10
1 5 6
6
6
8
8 7
8 8
3 9 7
7
9
8 6
7 7
3 9
1 6
47
12 51
15 7
7 15
38
17 34
17
34
15 32
13 7
7
10
9 7
6 9
3 10
56
14 46
14 7
8 12
64
15 57
9 6
6 8
16 8
7 14
3
9 5
5 9
9
7
15
16 6
5 14
2
9 6
6 8
54
16 30
10 5
7 8
32
15 33
14 5
8 16
34
14 35
9 6
7 9
34
15 31
17 6
7 15
60
15
34
14 28
15 6
7 13
29
13 35
16 54
2 1
1 2
14
12 6
9 12
2 12 6
9
8 6
6 8
16 9
6 13
3 16
1 1
1
2 1
1 2
1 6
1 1
1 6
1
1
2 1
1 3
7 6
6 9
15 6
7 14
2
9 6
6 8
8
5
8 5
7 9
14 6
8 15
2 14
1 1
1 1
3 1
1 2
56
16
31
12 32
12 6
10 14
55
16
35
14 43
15 8
7
9
5 8
4 9
3 10
41
16 28
15
30
16 38
14 7
6 17
36
11 38
8 8
6 9
40
17 36
13
13 7
7 15
3 14 8
6
12
16 6
6 13
2 16
60
17
29
14 35
11 6
6 17
54
15 67
14 6
6 16
36
14 39
18 59
14 6
7 17
52
14 58
6
9
9 8
6 8
3 10 7
8 17
1 5 5
7
6
15 7
9 13
1 5
61
13 59
13 6
6 13
37
16 38
15 58
13 5
4 16
31
13 33
18 59
12 6
7 12
74
15 63
15
15 7
7 17
3
9 6
6 9
7
7
9 6
6 8
15 7
7 14
1 14
51
15
42
13 37
13 7
6 14
59
16 54
14 8
6 16
36
14 37
19 57
14 7
6 10
52
13 65
43
13
28
13 34
10 5
9 15
44
13
29
13 35
14 7
5 14
50
14 62
14 6
6 14
60
15
31
16 44
13
14 8
7 14
3 13 5
5
17
11 7
7 15
2 15
34
11 31
16 59
13 6
7 12
58
15 51
16 7
6 16
31
15 39
12
36
14 40
15 5
6 17
32
14 40
10 7
7 10
41
17 35
5
13 8
6
9
10 7
7 9
3 10
1 5 5
6
5
9
8 7
8 8
3 9 7
7
10
8 5
7 7
4 9
1 5
47
12 51
15 7
7 15
38
16 34
16
34
15 32
13 8
7
12
8 6
6 9
3 10
56
14 46
14 8
8 12
64
15 57
11 6
6 8
15 9
7 14
3
10 5
5 9
7
7
16
16 7
5 15
2
9 6
6 9
54
15 30
10 5
7 8
32
14 33
13 5
8 16
34
14 35
9 6
7 9
34
15 31
17 5
7 15
60
15
34
13 28
14 5
7 13
29
13 35
15 54
1 1
1 2
14
12 6
9 11
2 12 5
9
9 5
6 8
16 10
6 13
3 16
1 2 1
1 2
1 6
1
1 6
1
1
2 1
1 2
8 5
6 9
15 8
7 14
3
9 6
6 8
8
5
9 5
7 9
14 7
8 15
2 14
1 1
1
2 1
1 1
56
15
31
12 32
12 6
10 13
55
16
35
14 43
15 8
7
10
5 9
4 9
3 10
41
16 28
9 4
8 7
30
16 38
14 7
6 17
36
11 38
8 8
6 9
40
17 36
13
13 6
7 15
3 14 8
6
13
16 6
6 13
1 16
60
16
29
14 35
11 8
6 17
54
15 67
13 5
6 16
36
14 39
17 59
14 6
7 17
52
14 58
6
10
9 8
6 8
3 10 7
8 16
1 4 5
7
5
15 6
9 13
1 5
61
13 59
12 6
6 13
37
16 38
15 58
13 5
4 16
31
12 33
18 59
12 5
7 12
74
14 63
14
15 8
7 18
2
10 6
6 8
5
7
11 6
6 8
15 6
7 14
2 14
51
15
42
13 37
12 8
6 14
59
15 54
13 8
6 15
36
13 37
19 57
15 6
6 10
52
13 65
H-matrix approximations of the exponential covariance matrix
(left), its hierarchical Cholesky factor ˜L (middle), and the zoomed
upper-left corner of the matrix (right), n = 4000, = 0.09,
ν = 0.5, σ2 = 1.
The adaptive-rank arithmetic is used, the relative accuracy in each sub-block is 1e − 5. Green blocks indicate
low-rank matrices, the number inside of each block indicates the maximal rank in this block. Very small dark-red
blocks are dense blocks, in this example they are located only on the diagonal. The “stairs” inside blocks indicate
decay of singular values in log-scale.
12

13. 4*
H-matrices (Hackbusch ’99), main steps
1. Build cluster tree TI and block cluster tree TI×I .
I
I
I I
I
I
I I I I1
1
2
2
11 12 21 22
I11
I12
I21
I22
13

14. 4*
Admissible condition
2. For each (t × s) ∈ TI×I , t, s ∈ TI , check
admissibility condition
min{diam(Qt), diam(Qs)} ≤ η · dist(Qt, Qs).
if(adm=true) then M|t×s is a rank-k matrix
block
if(adm=false) then divide M|t×s further or de-
fine as a dense matrix block, if small enough.
Q
Qt
S
dist
H=
t
s
All steps: Grid → cluster tree (TI ) + admissibility condition →
block cluster tree (TI×I ) → H-matrix → H-matrix arithmetics.
14

15. 4*
Mat´ern covariance functions
Mat´ern covariance functions
C(θ) =
2σ2
Γ(ν)
r
2
ν
Kν
r
, θ = (σ2
, ν, ).
Cν=3/2(r) = 1 +
√
3r
exp −
√
3r
(1)
Cν=5/2(r) = 1 +
√
5r
+
5r2
3 2
exp −
√
5r
(2)
ν = 1/2 exponential covariance function Cν=1/2(r) = exp(−r),
ν → ∞ Gaussian covariance function Cν=∞(r) = exp(−r2).
15

16. 4*
Identifying unknown parameters
Identifying unknown parameters
16

17. 4*
Identifying unknown parameters
Given: Z = {Z(s1), . . . , Z(sn)} , where Z(s) is a Gaussian
random field indexed by a spatial location s ∈ Rd , d ≥ 1.
Assumption: Z has mean zero and stationary parametric
covariance function, e.g. Mat´ern:
C(θ) =
2σ2
Γ(ν)
r
2
ν
Kν
r
, θ = (σ2
, ν, ).
To identify: unknown parameters θ := (σ2, ν, ).
17

18. 4*
Identifying unknown parameters
Statistical inference about θ is then based on the Gaussian
log-likelihood function:
L(θ) = −
n
2
log(2π) −
1
2
log|C(θ)| −
1
2
Z C(θ)−1
Z, (3)
where the covariance matrix C(θ) has entries C(si − sj ; θ),
i, j = 1, . . . , n. The maximum likelihood estimator of θ is the value
θ that maximizes (3).
18

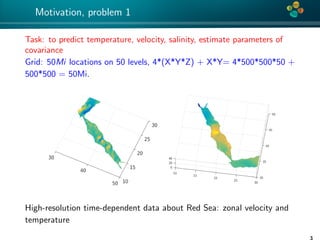
19. 4*
Details of the identification
To maximize the log-likelihood function we use the Brent’s method
[Brent’73] (combining bisection method, secant method and
inverse quadratic interpolation).
1. H-matrix: C(θ) ≈ C(θ, k) or ≈ C(θ, ε).
2. H-Cholesky: C(θ, k) = L(θ, k)L(θ, k)T
3. ZT C−1Z = ZT (LLT )−1Z = vT · v, where v is a solution of
L(θ, k)v(θ) := Z.
log det{C} = log det{LLT
} = log det{
n
i=1
λ2
i } = 2
n
i=1
logλi ,
L(θ, k) = −
N
2
log(2π) −
N
i=1
log{Lii (θ, k)} −
1
2
(v(θ)T
· v(θ)). (4)
19

20. Dependence of log-likelihood and its ingredients on parameters,
n = 4225. k = 8 in the first row and k = 16 in the second.
First column: = 0.2337 fixed; Second column: ν = 0.5 fixed.
20

21. 4*
Remark: stabilization with nugget
To avoid instability in computing Cholesky, we add: Cm = C + δ2I.
Let λi be eigenvalues of C, then eigenvalues of Cm will be λi + δ2,
log det(Cm) = log n
i=1(λi + δ2) = n
i=1 log(λi + δ2).
(left) Dependence of the negative log-likelihood on parameter
with nuggets {0.01, 0.005, 0.001} for the Gaussian covariance.
(right) Zoom of the left figure near minimum; n = 2000 random
points from moisture example, rank k = 14, σ2 = 1, ν = 0.5.
21

22. 4*
Error analysis
Theorem (1)
Let C be an H-matrix approximation of matrix C ∈ Rn×n such that
ρ(C−1
C − I) ≤ ε < 1.
Then
|log|C| − log|C|| ≤ −nlog(1 − ε), (5)
Proof: See [Ballani, Kressner 14] and [Ipsen 05].
Remark: factor n is pessimistic and is not really observed
numerically.
22

23. 4*
Error in the log-likelihood
Theorem (2)
Let C ≈ C ∈ Rn×n and Z be a vector, Z ≤ c0 and C−1 ≤ c1.
Let ρ(C−1C − I) ≤ ε < 1. Then it holds
|L(θ) − L(θ)| =
1
2
(log|C| − log|C|) +
1
2
|ZT
C−1
− C−1
Z|
≤ −
1
2
· nlog(1 − ε) +
1
2
|ZT
C−1
C − C−1
C C−1
Z|
≤ −
1
2
· nlog(1 − ε) +
1
2
c2
0 · c1 · ε.
23

24. 2 4 6 8 10
0.55
0.6
0.65
0.7
0.75
0.8
0.85
2 4 6 8 10
0.55
0.6
0.65
0.7
0.75
0.8
0.85
2 4 6 8 10
0.55
0.6
0.65
0.7
0.75
0.8
0.85
Functional boxplots of the estimated parameters as a function of
the accuracy ε, based on 50 replicates with
n = {4000, 8000, 32000} observations (left to right columns). True
parameters θ∗
= ( , ν, σ2) = (0.7, 0.9, 1.0) represented by the
green dotted lines.
24

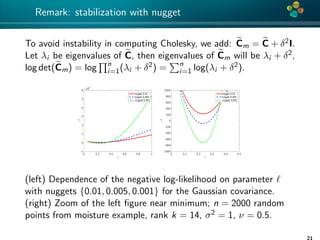
25. 4*
How much memory is needed?
0 0.5 1 1.5 2 2.5
ℓ, ν = 0.325, σ2
= 0.98
5
5.5
6
6.5
size,inbytes
×10 6
1e-4
1e-6
0.2 0.4 0.6 0.8 1 1.2 1.4
ν, ℓ = 0.58, σ2
= 0.98
5.2
5.4
5.6
5.8
6
6.2
6.4
6.6
size,inbytes
×10 6
1e-4
1e-6
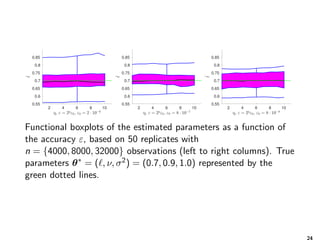
(left) Dependence of the matrix size on the covariance length ,
and (right) the smoothness ν for two different accuracies in the
H-matrix sub-blocks ε = {10−4, 10−6}, for n = 2, 000 locations in
the domain [32.4, 43.4] × [−84.8, −72.9].
25

26. 4*
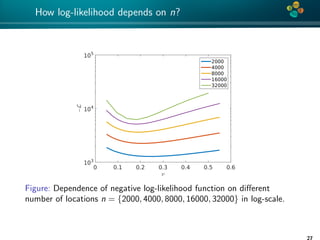
Error convergence
0 10 20 30 40 50 60 70 80 90 100
−25
−20
−15
−10
−5
0
rank k
log(rel.error)
Spectral norm, L=0.1, nu=1
Frob. norm, L=0.1
Spectral norm, L=0.2
Frob. norm, L=0.2
Spectral norm, L=0.5
Frob. norm, L=0.5
0 10 20 30 40 50 60 70 80 90 100
−16
−14
−12
−10
−8
−6
−4
−2
0
rank k
log(rel.error)
Spectral norm, L=0.1, nu=0.5
Frob. norm, L=0.1
Spectral norm, L=0.2
Frob. norm, L=0.2
Spectral norm, L=0.5
Frob. norm, L=0.5
Convergence of the H-matrix approximation errors for covariance
lengths {0.1, 0.2, 0.5}; (left) ν = 1 and (right) ν = 0.5,
computational domain [0, 1]2.
26

27. 4*
How log-likelihood depends on n?
Figure: Dependence of negative log-likelihood function on different
number of locations n = {2000, 4000, 8000, 16000, 32000} in log-scale.
27

28. 4*
Time and memory for parallel H-matrix approximation
Maximal # cores is 40, ν = 0.325, = 0.64, σ2 = 0.98
n ˜C ˜L˜L
time size kB/dof time size I − (˜L˜L )−1 ˜C 2
sec. MB sec. MB
32,000 3.3 162 5.1 2.4 172.7 2.4 · 10−3
128,000 13.3 776 6.1 13.9 881.2 1.1 · 10−2
512,000 52.8 3420 6.7 77.6 4150 3.5 · 10−2
2,000,000 229 14790 7.4 473 18970 1.4 · 10−1
28

29. 4*
Parameter identification
64 32 16 8 4 2
n, samples in thousands
0.07
0.08
0.09
0.1
0.11
0.12
ℓ
64 32 16 8 4 2
n, samples in thousands
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.7
ν
Synthetic data with known parameters. Boxplots for and ν for
n = 1, 000 × {64, 32, ..., 4, 2}; 100 replicates.
29

30. 4*
Parameter estimation vs H-matrix accuracy
10 -7
10 -6
10 -5
10 -4
0.55
0.6
0.65
0.7
0.75
0.8
32000
truth
10 -7
10 -6
10 -5
10 -4
0.88
0.89
0.9
0.91
0.92
32000
truth
10 -7
10 -6
10 -5
10 -4
0.8
1
1.2
32000
truth
Estimated parameters as a function of the accuracy ε, based on 30
replicates (black solid curves) with n = 32,000 observations. True
parameters θ = ( , ν, σ2) = (0.7, 0.9.1.0) represented by the green
doted lines. Replicates on (a) identify ˆ; on (b) identify ˆν; and on
(c) identify ˆσ2.
30

31. 4*
Canonical (left) and Tucker (right) decompositions of 3D tensors.
Canonical (left) and Tucker (right) decompositions
of tensors.
31

32. 4*
Canonical (left) and Tucker (right) decompositions of 3D tensors.
R
(3)
1
(2)
2
(1)
1
(3)
R
(2)
R
(1)
R
.
.
b
c1
u
u
u u
u
u
c+ . . . +
A
n3
n1
n2
r3
3
2
r
1
r
r
r1
B
1
3
2
r
2
A
V
(1)
V
(2)
V
(3)
n
n
n
n
1
n
3
n
2
I
I
I
2
3
1
I3
A
I2
A(1)I
1
[A. Litvinenko, D. Keyes, V. Khoromskaia, B. N. Khoromskij, H. G. Matthies, Tucker Tensor Analysis of Mat´ern
Functions in Spatial Statistics, 2018]
32

33. 4*
Approximating Mat´ern covariance in a low-rank tensor format
≈ r
i=1
d
µ=1 Ciµ
≈ R
i=1
d
ν=1 ˜uiν
Cν, (r) = 21−ν
Γ(ν)
√
2νr
ν
Kν
√
2νr
fα,ν(ρ) := Γ(ν+d/2)α2ν
πd/2Γ(ν)
1
(α2+ρ2)ν+d/2
?
IFFT
Low-rank
approximation
FFT
Two possible ways to find a low rank approximation of the Mat´ern
covariance matrix. The Fourier transformation is analytically
known and has known low-rank approximation. The inverse Fourier
transformation (IFFT) can be computed numerically and does not
change the rank.
33

34. 4*
Convergence
fα,ν(ρ) :=
C
(α2 + ρ2)ν+d/2
, (6)
where α ∈ (0.1, 100) and d = 1, 2, 3.
Tucker rank
5 10 15
Frobeniuserror
10 -10
10 -5
10 0 SD Matern, α = 0.1
ν=0.1
ν=0.2
ν=0.4
ν=0.8
Tucker rank
5 10 15
Frobeniuserror
10 -20
10 -15
10 -10
10 -5 SD Matern, α = 100
ν=0.1
ν=0.2
ν=0.4
ν=0.8
Figure: Convergence w.r.t the Tucker rank of 3D spectral density of
Mat´ern covariance (6) with α = 0.1 (left) and α = 100 (right).
34

35. 4*
Example of a very large problem
n = 100 n = 500 n = 1000
d = 1000 3.7 67 491
Table: Computing time (in sec.) to set up and to compute the trace of
˜C =
R
j=1
d
ν=1 Cjν, R = 10. Matrix ˜C is of size N × N, where N = nd
,
d = 1000 and n = {100, 500, 1000}. A linux cluster with 40 processors
and 128 GB RAM was used.
Example 2: Cholesky decomposition of the Gaussian covariance
matrix in 3D. A numerical experiment contains a grid with 60003
mesh points. The algorithm requires 15 seconds (11 seconds for
matrix setup and 4 seconds for Cholesky).
35

36. 4*
Properties
Let cov(x, y) = exp−|x−y|2
, where
x = (x1, .., xd ), y = (y1, ..., yd ) ∈ D ∈ R3.
cov(x, y) = exp−|x1−y1|2
⊗ exp−|x2−y2|2
⊗ exp−|x3−y3|2
.
C = C1 ⊗ ... ⊗ Cd .
If d Cholesky decompositions exist, i.e, Ci = Li · LT
i , i = 1..d.
Then
C1⊗...⊗Cd = (L1LT
1 )⊗...⊗(Ld LT
d ) = (L1⊗...⊗Ld )·(LT
1 ⊗...⊗LT
d ) =: L·LT
where L := L1 ⊗ ... ⊗ Ld , LT := LT
1 ⊗ ... ⊗ LT
d are also low- and
upper-triangular matrices.
(C1 ⊗ ... ⊗ Cd )−1
= C−1
1 ⊗ ... ⊗ C−1
d .
Reduced from O(NlogN), N = nd , to O(dnlogn).

37. 4*
Properties
Let C ≈ ˜C = r
i=1
d
µ=1 Ciµ, then
diag(˜C) = diag


r
i=1
d
µ=1
Ciµ

 =
r
i=1
d
µ=1
diag (Ciµ) , (7)
trace(˜C) = trace


r
i=1
d
µ=1
Ciµ

 =
r
i=1
d
µ=1
trace(Ciµ). (8)
det(C1 ⊗ C2) = det(C1)n2
· det(C2)n1
log det(C1⊗C2) = log(det(C1)n2
·det(C2)n1
) = n2log det C1+n1log det C2.
log det(C1⊗C2⊗C3) = n2n3log det C1+n1n3log det C2+n1n2log det C3.
37

38. 4*
Log-Likelihood in tensor format
L = −
n1n2n3
2
log(2π)−n2n3log det C1−n1n3log det C2−n1n2log det C3
−
r
i=1
r
j=1
(uT
i uj )(wT
i wj ).
38

39. 4*
Conclusion
Sparse, low-rank, hierarchical (pros and cons)
Approximated Mat´ern covariance
Provided error estimate of L − L .
Researched influence of H-matrix approximation error on the
estimated parameters (boxplots).
With application of H-matrices
we extend the class of covariance functions to work with,
we allow non-regular discretization of the covariance function
on large spatial grids.
tensor rank is not equal to the matrix rank
matrix rank splits x from y and tensor rank splits (xi − yi )
from (xj − yj ), i, j > 1, i = j.

40. 4*
Literature
1. A. Litvinenko, HLIBCov: Parallel Hierarchical Matrix Approximation of Large Covariance Matrices and
Likelihoods with Applications in Parameter Identification, preprint arXiv:1709.08625, 2017
2. A. Litvinenko, Y. Sun, M.G. Genton, D. Keyes, Likelihood Approximation With Hierarchical Matrices For Large
Spatial Datasets, preprint arXiv:1709.04419, 2017
3. B.N. Khoromskij, A. Litvinenko, H.G. Matthies, Application of hierarchical matrices for computing the
Karhunen-Lo´eve expansion, Computing 84 (1-2), 49-67, 31, 2009
4. H.G. Matthies, A. Litvinenko, O. Pajonk, B.V. Rosi´c, E. Zander, Parametric and uncertainty computations with
tensor product representations, Uncertainty Quantification in Scientific Computing, 139-150, 2012
5. W. Nowak, A. Litvinenko, Kriging and spatial design accelerated by orders of magnitude: Combining low-rank
covariance approximations with FFT-techniques, Mathematical Geosciences 45 (4), 411-435, 2013
6. P. Waehnert, W.Hackbusch, M. Espig, A. Litvinenko, H. Matthies: Efficient low-rank approximation of the
stochastic Galerkin matrix in the tensor format, Computers & Mathematics with Applications, 67 (4), 818-829,
2014
7. M. Espig, W. Hackbusch, A. Litvinenko, H.G. Matthies, E. Zander, Efficient analysis of high dimensional data in
tensor formats, Sparse Grids and Applications, 31-56, Springer, Berlin, 2013
8. A. Litvinenko, D. Keyes, V. Khoromskaia, B. N. Khoromskij, H. G. Matthies, Tucker Tensor Analysis of Mat´ern
Functions in Spatial Statistics, DOI: https://doi.org/10.1515/cmam-2018-0022, Computational Methods in
Applied Mathematics , 2018
40

41. 4*
Literature
9. S. Dolgov, B.N. Khoromskij, A. Litvinenko, H.G. Matthies, Computation of the Response Surface in the
Tensor Train data format arXiv preprint arXiv:1406.2816, 2014
10. S. Dolgov, B.N. Khoromskij, A. Litvinenko, H.G. Matthies, Polynomial Chaos Expansion of Random
Coefficients and the Solution of Stochastic Partial Differential Equations in the Tensor Train Format,
IAM/ASA J. Uncertainty Quantification 3 (1), 1109-1135, 2015
11. A. Litvinenko, Application of Hierarchical matrices for solving multiscale problems, PhD Thesis, Leipzig
University, Germany, https://www.wire.tu-bs.de/mitarbeiter/litvinen/diss.pdf, 2006
12. B.N. Khoromskij, A. Litvinenko, Domain decomposition based H-matrix preconditioners for the skin
problem, Domain Decomposition Methods in Science and Engineering XVII, pp 175-182, 2006
41

42. 4*
Used Literature and Slides
Book of W. Hackbusch 2012,
Dissertations of I. Oseledets and M. Espig
Articles of Tyrtyshnikov et al., De Lathauwer et al., L.
Grasedyck, B. Khoromskij, M. Espig
Lecture courses and presentations of Boris and Venera
Khoromskij
Software T. Kolda et al.; M. Espig et al.; D. Kressner, K.
Tobler; I. Oseledets et al.
42

43. 4*
Tensor Software
Ivan Oseledets et al., Tensor Train toolbox (Matlab),
http://spring.inm.ras.ru/osel
D.Kressner, C. Tobler, Hierarchical Tucker Toolbox (Matlab),
http://www.sam.math.ethz.ch/NLAgroup/htucker toolbox.html
M. Espig, et al
Tensor Calculus library (C): http://gitorious.org/tensorcalculus
43

44. 4*
Acknowledgement
1. Ronald Kriemann (MPI Leipzig) for www.hlibpro.com
2. KAUST Research Computing group, KAUST Supercomputing
Lab (KSL)
44