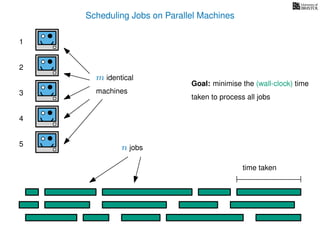
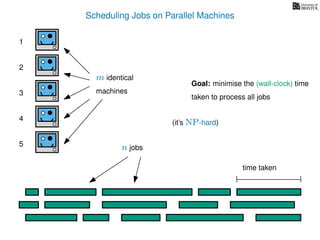
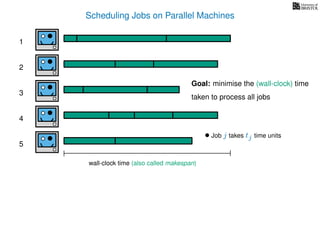
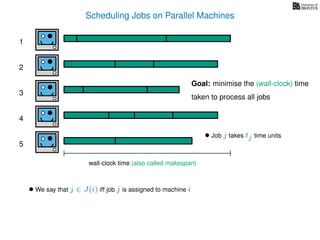
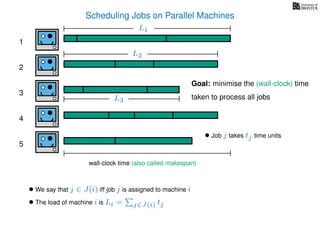
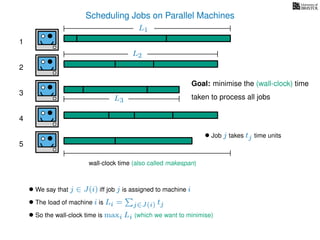
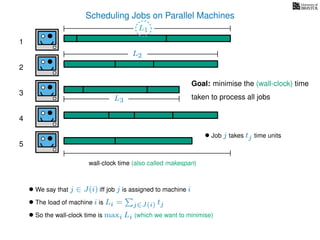
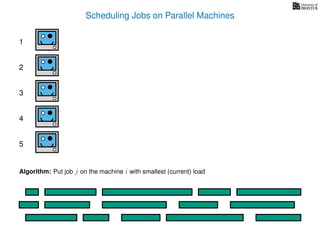
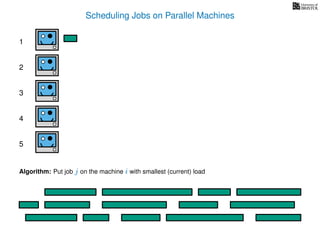
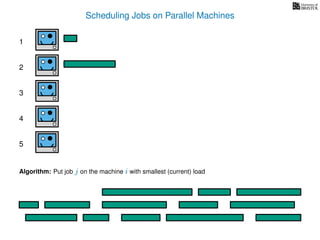
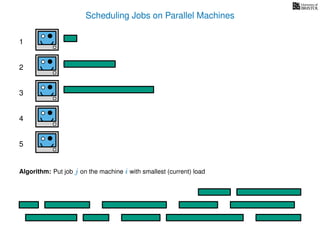
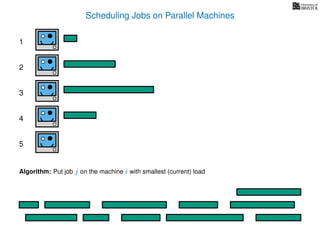
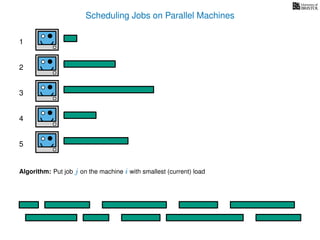
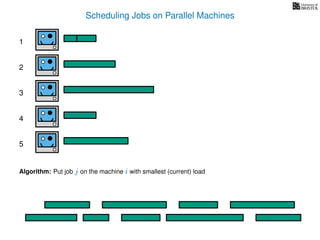
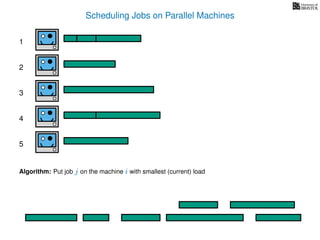
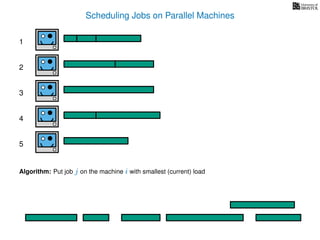
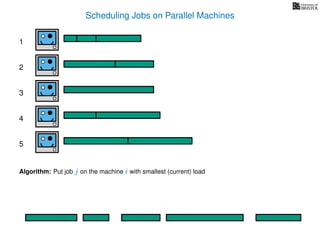
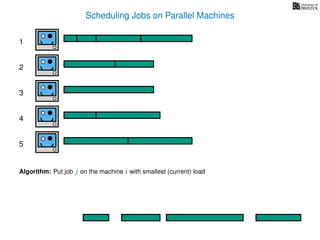
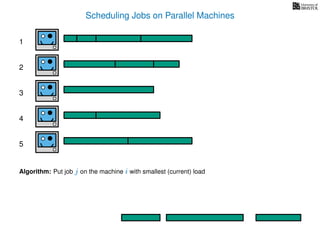
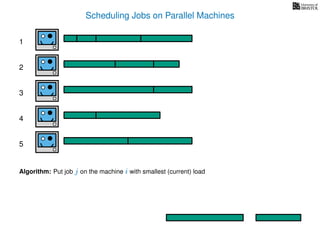
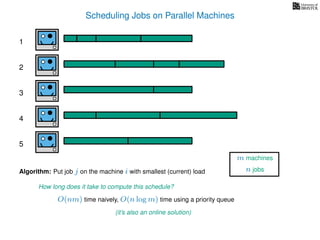
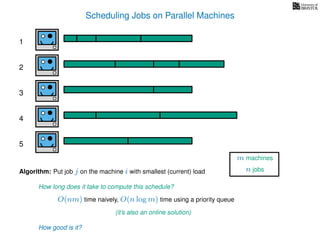
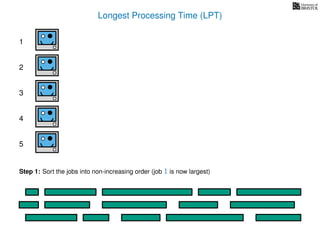
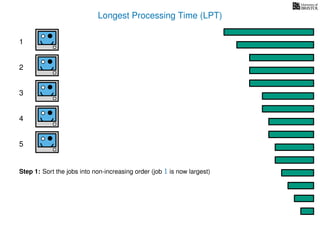
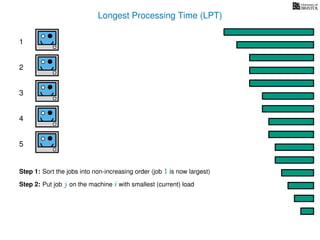
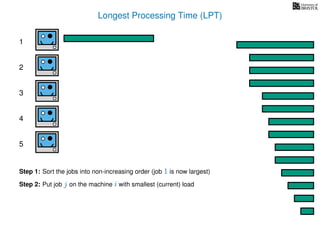
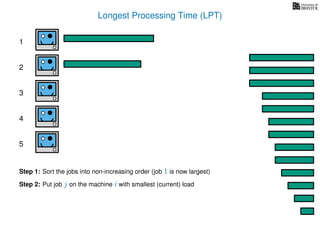
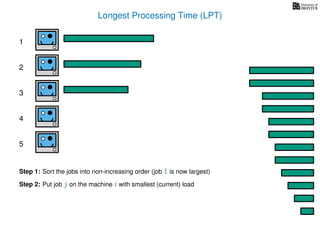
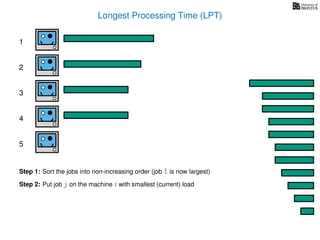
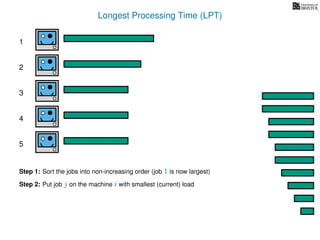
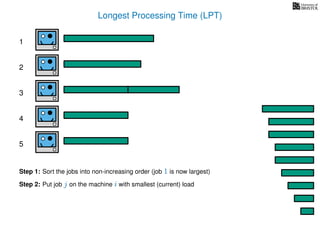
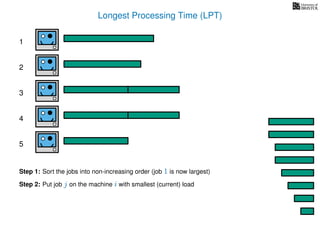
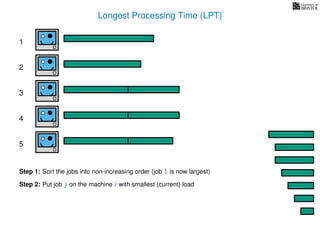
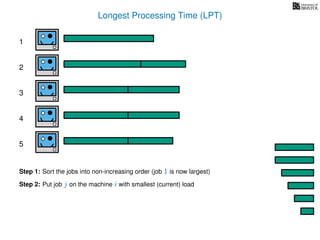
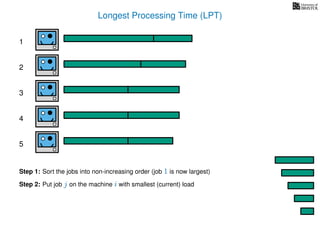
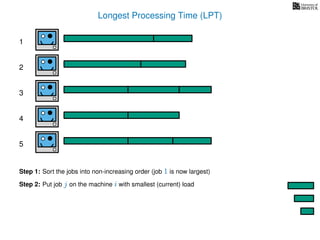
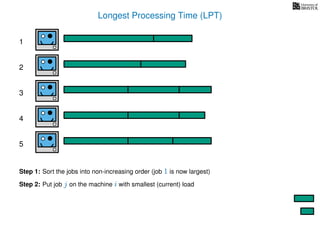
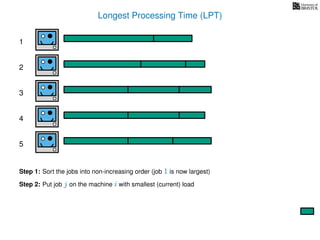
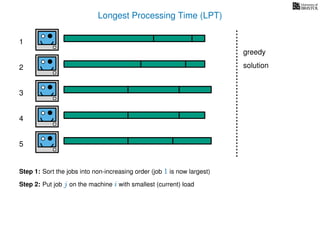
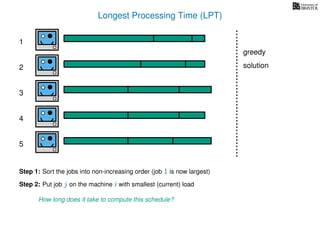
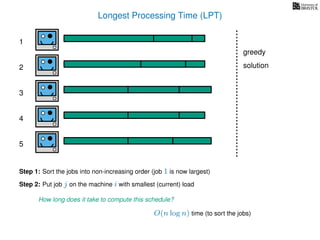
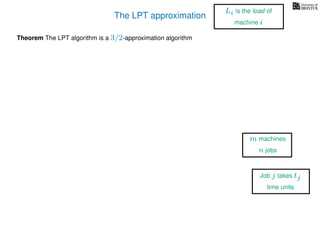
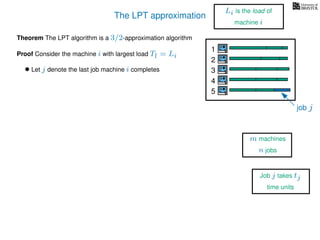
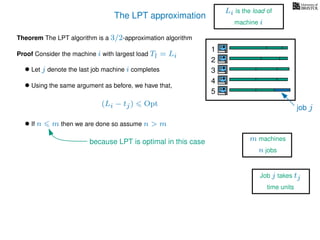
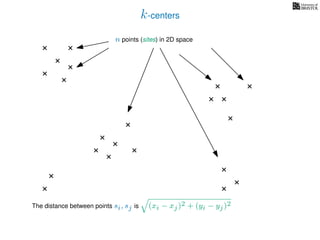
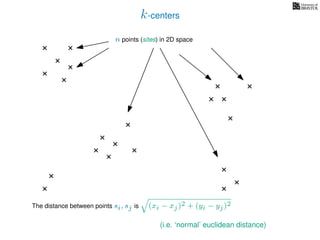
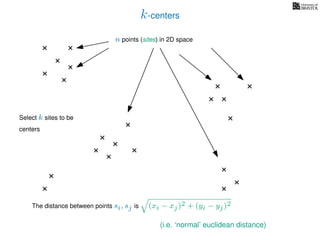
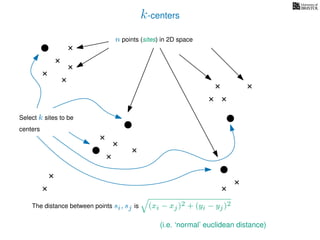
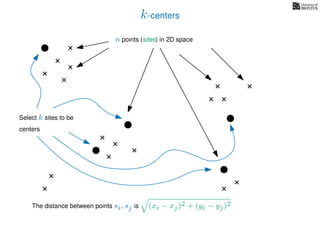
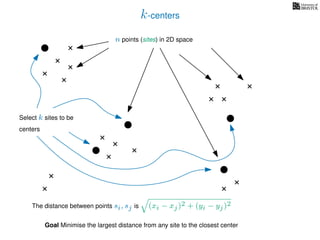
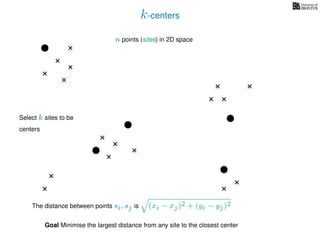
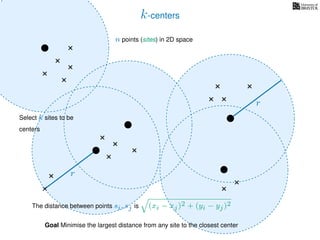
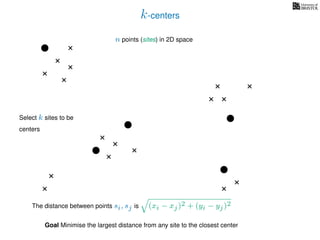
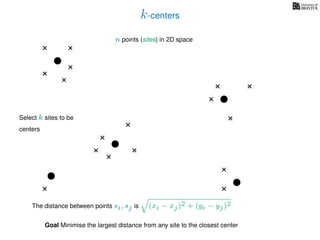
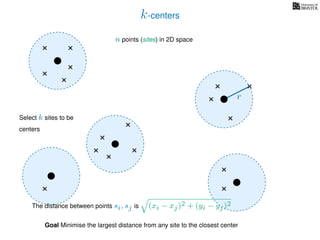
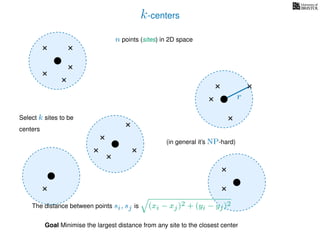
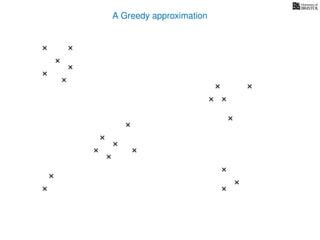
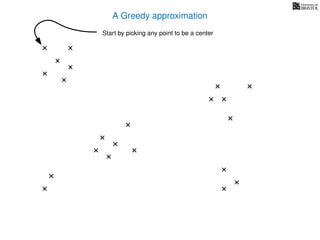
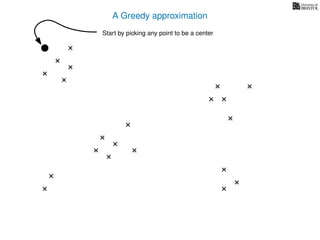
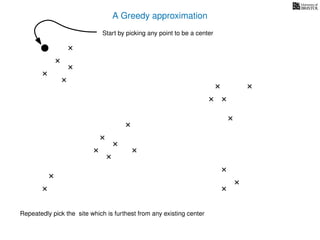
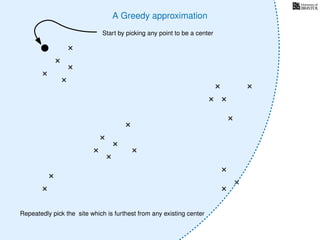
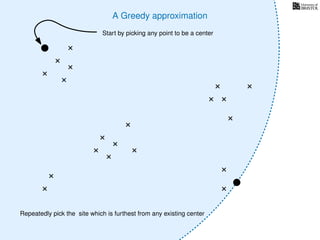
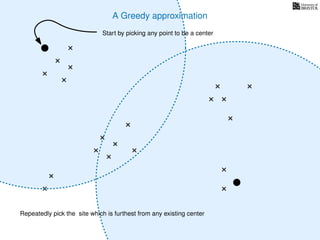
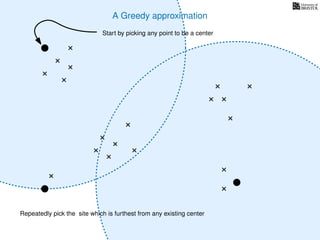
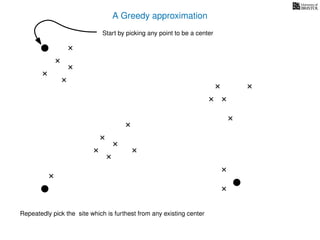
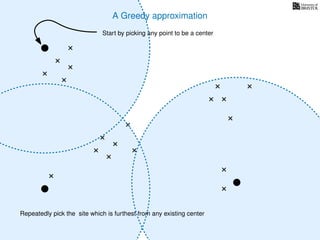
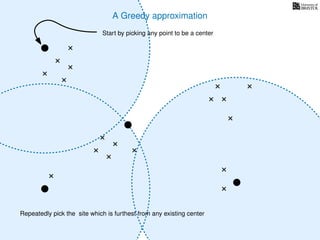
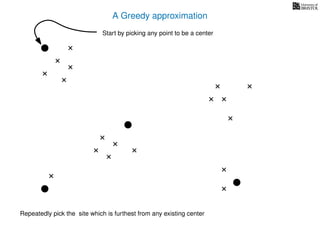
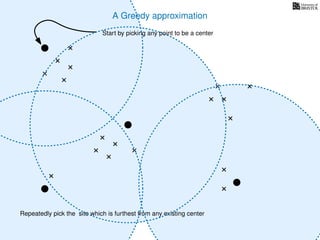
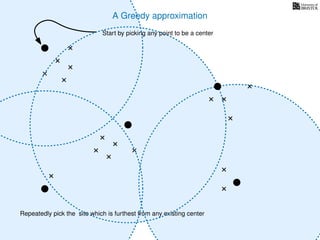
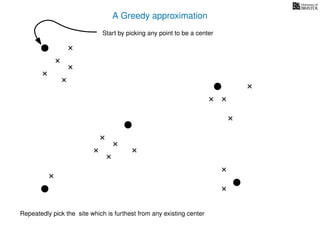
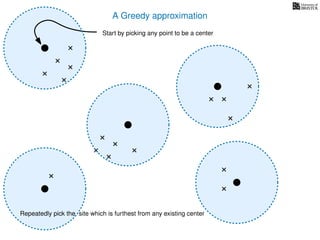
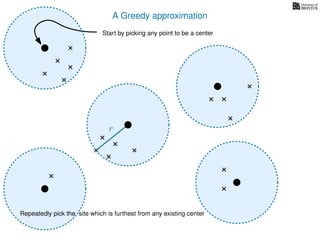
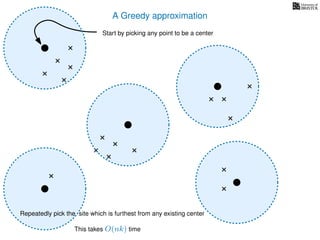
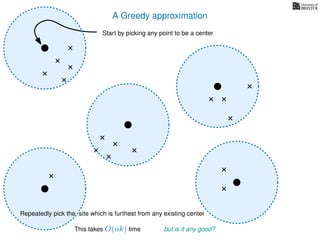
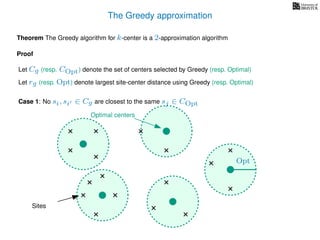
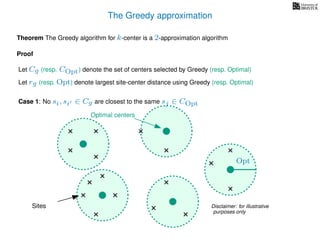
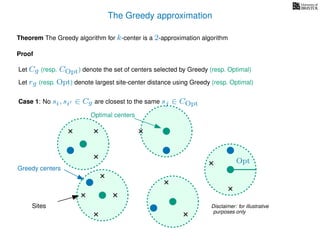
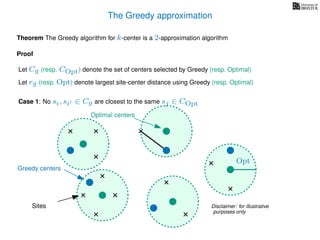
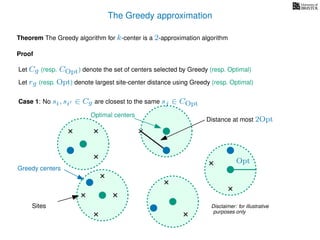
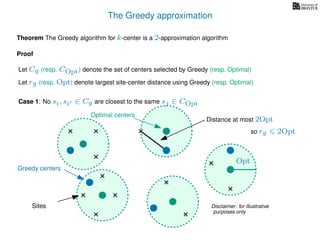
The document discusses approximation algorithms, particularly focusing on scheduling jobs on parallel machines to minimize wall-clock time, also known as makespan. It introduces a greedy algorithm that serves as a 2-approximation method for job scheduling, detailing how jobs can be assigned to machines with the smallest current load. The document outlines the computational efficiency of this approach, comparing naive and optimized methods for scheduling.

1. Advanced Algorithms – COMS31900
Approximation algorithms part two
more constant factor approximations
Benjamin Sach

2. Approximation Algorithms Recap
An algorithm A is an α-approximation algorithm for problem P if,
◦ A runs in polynomial time
◦ A always outputs a solution with value s
Here P is an optimisation problem with optimal solution of value Opt
• If P is a maximisation problem,
Opt
α s Opt
within an α factor of Opt
• If P is a minimisation problem, Opt s α · Opt
We have seen
a 3/2-approximation algorithm for Bin Packing
(and a faster 2-approximation)

3. Scheduling Jobs on Parallel Machines
1
2
3
4
5
m identical
machines
n jobs
time taken
Goal: minimise the (wall-clock) time
taken to process all jobs

4. Scheduling Jobs on Parallel Machines
1
2
3
4
5
m identical
machines
n jobs
time taken
Goal: minimise the (wall-clock) time
taken to process all jobs
(it’s NP-hard)

5. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Goal: minimise the (wall-clock) time
taken to process all jobs
wall-clock time (also called makespan)

6. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Goal: minimise the (wall-clock) time
taken to process all jobs
wall-clock time (also called makespan)
• Job j takes tj time units

7. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Goal: minimise the (wall-clock) time
taken to process all jobs
wall-clock time (also called makespan)
• We say that j ∈ J(i) iff job j is assigned to machine i
• Job j takes tj time units

8. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Goal: minimise the (wall-clock) time
taken to process all jobs
wall-clock time (also called makespan)
• We say that j ∈ J(i) iff job j is assigned to machine i
• The load of machine i is Li = j∈J(i) tj
• Job j takes tj time units

9. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Goal: minimise the (wall-clock) time
taken to process all jobs
wall-clock time (also called makespan)
• We say that j ∈ J(i) iff job j is assigned to machine i
• The load of machine i is Li = j∈J(i) tj
• Job j takes tj time units
L2
L3
L1

10. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Goal: minimise the (wall-clock) time
taken to process all jobs
wall-clock time (also called makespan)
• We say that j ∈ J(i) iff job j is assigned to machine i
• The load of machine i is Li = j∈J(i) tj
• Job j takes tj time units
• So the wall-clock time is maxi Li (which we want to minimise)
L2
L3
L1

11. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Goal: minimise the (wall-clock) time
taken to process all jobs
wall-clock time (also called makespan)
• We say that j ∈ J(i) iff job j is assigned to machine i
• The load of machine i is Li = j∈J(i) tj
• Job j takes tj time units
• So the wall-clock time is maxi Li (which we want to minimise)
L2
L3
L1L1

12. Scheduling Jobs on Parallel Machines
1
2
3
4
5

13. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

14. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

15. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

16. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

17. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

18. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

19. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

20. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

21. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

22. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

23. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

24. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

25. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

26. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

27. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

28. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load

29. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load
How long does it take to compute this schedule?

30. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load
How long does it take to compute this schedule?
m machines
n jobs

31. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load
How long does it take to compute this schedule?
O(nm) time naively, O(n log m) time using a priority queue
m machines
n jobs

32. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load
How long does it take to compute this schedule?
O(nm) time naively, O(n log m) time using a priority queue
(it’s also an online solution)
m machines
n jobs

33. Scheduling Jobs on Parallel Machines
1
2
3
4
5
Algorithm: Put job j on the machine i with smallest (current) load
How long does it take to compute this schedule?
O(nm) time naively, O(n log m) time using a priority queue
How good is it?
(it’s also an online solution)
m machines
n jobs

34. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Job j takes tj
time units
Li is the load of
machine i
m machines
n jobs

35. The greedy approximation
• Before we prove this, we prove two useful facts,
Theorem The greedy algorithm given is a 2-approximation algorithm
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Job j takes tj
time units
Li is the load of
machine i
m machines
n jobs

36. The greedy approximation
• Before we prove this, we prove two useful facts,
Fact Opt maxj tj
Theorem The greedy algorithm given is a 2-approximation algorithm
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Job j takes tj
time units
Li is the load of
machine i
m machines
n jobs

37. The greedy approximation
• Before we prove this, we prove two useful facts,
Fact Opt maxj tj
◦ Some machine must process the largest job
Theorem The greedy algorithm given is a 2-approximation algorithm
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Job j takes tj
time units
Li is the load of
machine i
m machines
n jobs

38. The greedy approximation
• Before we prove this, we prove two useful facts,
Fact Opt maxj tj
Fact Opt j tj
m
◦ Some machine must process the largest job
Theorem The greedy algorithm given is a 2-approximation algorithm
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Job j takes tj
time units
Li is the load of
machine i
m machines
n jobs

39. The greedy approximation
• Before we prove this, we prove two useful facts,
Fact Opt maxj tj
Fact Opt j tj
m
◦ Some machine must process the largest job
◦ There is a total of j tj time units of work to be done
Theorem The greedy algorithm given is a 2-approximation algorithm
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Job j takes tj
time units
Li is the load of
machine i
m machines
n jobs

40. The greedy approximation
• Before we prove this, we prove two useful facts,
Fact Opt maxj tj
Fact Opt j tj
m
◦ Some machine must process the largest job
◦ There is a total of j tj time units of work to be done
◦ Some machine i must have load Li at least
j tj
m
Theorem The greedy algorithm given is a 2-approximation algorithm
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Job j takes tj
time units
Li is the load of
machine i
m machines
n jobs

41. The greedy approximation
• Before we prove this, we prove two useful facts,
Fact Opt maxj tj
Fact Opt j tj
m
◦ Some machine must process the largest job
◦ There is a total of j tj time units of work to be done
◦ Some machine i must have load Li at least
j tj
m
(the m machines can’t all have below average load)
Theorem The greedy algorithm given is a 2-approximation algorithm
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Job j takes tj
time units
Li is the load of
machine i
m machines
n jobs

42. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
m machines
n jobs

43. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
Proof Consider the machine i with largest load Tg = Li
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
m machines
n jobs

44. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
Proof Consider the machine i with largest load Tg = Li
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs

45. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs

46. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

47. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

48. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs

49. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

50. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
So. . .
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

51. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Li − tj Lk for all 1 k m,
So. . .
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

52. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Li − tj Lk for all 1 k m,
So. . .
• If we then sum over all k,
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

53. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Li − tj Lk for all 1 k m,
So. . .
• If we then sum over all k,
m(Li − tj)
m
k=1
Lk
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

54. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Li − tj Lk for all 1 k m,
So. . .
• If we then sum over all k,
m(Li − tj)
m
k=1
Lk
so (Li − tj)
m
k=1 Lk
m Opt (by the second fact)
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

55. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Li − tj Lk for all 1 k m,
So. . .
• If we then sum over all k,
m(Li − tj)
m
k=1
Lk
so (Li − tj)
m
k=1 Lk
m Opt (by the second fact)
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j
Fact Opt j tj
m

56. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Li − tj Lk for all 1 k m,
So. . .
• If we then sum over all k,
m(Li − tj)
m
k=1
Lk
so (Li − tj)
m
k=1 Lk
m Opt (by the second fact)
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

57. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Li − tj Lk for all 1 k m,
So. . .
• If we then sum over all k,
m(Li − tj)
m
k=1
Lk
so (Li − tj)
m
k=1 Lk
m Opt (by the second fact)
also tj Opt (by the first fact)
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

58. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Li − tj Lk for all 1 k m,
So. . .
• If we then sum over all k,
m(Li − tj)
m
k=1
Lk
so (Li − tj)
m
k=1 Lk
m Opt (by the second fact)
also tj Opt (by the first fact)
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j
Fact Opt maxj tj

59. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Li − tj Lk for all 1 k m,
So. . .
• If we then sum over all k,
m(Li − tj)
m
k=1
Lk
so (Li − tj)
m
k=1 Lk
m Opt (by the second fact)
also tj Opt (by the first fact)
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

60. The greedy approximation
Theorem The greedy algorithm given is a 2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tg = Li
• When job j was assigned, machine i had the smallest load, Li − tj
Li − tj Lk for all 1 k m,
So. . .
• If we then sum over all k,
m(Li − tj)
m
k=1
Lk
so (Li − tj)
m
k=1 Lk
m Opt (by the second fact)
also tj Opt (by the first fact)
Therefore, Tg = Li = (Li − tj) + tj Opt + Opt = 2Opt
Let Opt denote the time taken by the optimal scheduling of jobs
Let Tg denote the time taken by the greedy schedule
Li is the load of
machine i
Job j takes tj
time units
1
2
3
4
5
Li = Tg
m machines
n jobs
job j

61. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)

62. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)

63. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

64. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

65. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

66. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

67. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

68. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

69. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

70. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

71. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

72. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

73. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

74. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

75. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

76. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

77. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

78. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load

79. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load
greedy
solution

80. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load
greedy
solution
How long does it take to compute this schedule?

81. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load
greedy
solution
How long does it take to compute this schedule?
O(n log n) time (to sort the jobs)

82. Longest Processing Time (LPT)
1
2
3
4
5
Step 1: Sort the jobs into non-increasing order (job 1 is now largest)
Step 2: Put job j on the machine i with smallest (current) load
greedy
solution
How long does it take to compute this schedule?
O(n log n) time (to sort the jobs)
How good is it?

83. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let Tl denote the time taken by the LPT schedule
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units

84. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Before we prove this, we prove another useful fact and a Lemma
• Let Tl denote the time taken by the LPT schedule
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units

85. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Before we prove this, we prove another useful fact and a Lemma
Fact If there are at most m jobs (n m) then LPT is optimal
• Let Tl denote the time taken by the LPT schedule
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units

86. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Before we prove this, we prove another useful fact and a Lemma
Fact If there are at most m jobs (n m) then LPT is optimal
LPT gives each job its own machine so maxi Li maxj tj Opt
• Let Tl denote the time taken by the LPT schedule
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
If there are at most m jobs then

87. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Before we prove this, we prove another useful fact and a Lemma
Fact If there are at most m jobs (n m) then LPT is optimal
Lemma If n > m then Opt 2t(m+1) (after sorting)
LPT gives each job its own machine so maxi Li maxj tj Opt
• Let Tl denote the time taken by the LPT schedule
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
If there are at most m jobs then

88. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Before we prove this, we prove another useful fact and a Lemma
Fact If there are at most m jobs (n m) then LPT is optimal
Lemma If n > m then Opt 2t(m+1) (after sorting)
LPT gives each job its own machine so maxi Li maxj tj Opt
• Let Tl denote the time taken by the LPT schedule
Proof
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
If there are at most m jobs then

89. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Before we prove this, we prove another useful fact and a Lemma
Fact If there are at most m jobs (n m) then LPT is optimal
Lemma If n > m then Opt 2t(m+1) (after sorting)
LPT gives each job its own machine so maxi Li maxj tj Opt
◦ Note that t1 t2 t3 . . . tm t(m+1)
• Let Tl denote the time taken by the LPT schedule
Proof
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
If there are at most m jobs then

90. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Before we prove this, we prove another useful fact and a Lemma
Fact If there are at most m jobs (n m) then LPT is optimal
Lemma If n > m then Opt 2t(m+1) (after sorting)
LPT gives each job its own machine so maxi Li maxj tj Opt
◦ Note that t1 t2 t3 . . . tm t(m+1)
◦ One of the m machines must be assigned
• Let Tl denote the time taken by the LPT schedule
Proof
(at least) two of these m + 1 jobs under any schedule
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
If there are at most m jobs then

91. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Before we prove this, we prove another useful fact and a Lemma
Fact If there are at most m jobs (n m) then LPT is optimal
Lemma If n > m then Opt 2t(m+1) (after sorting)
LPT gives each job its own machine so maxi Li maxj tj Opt
◦ Note that t1 t2 t3 . . . tm t(m+1)
◦ One of the m machines must be assigned
• Let Tl denote the time taken by the LPT schedule
Proof
(at least) two of these m + 1 jobs under any schedule
◦ So we have that any schedule takes at least 2t(m+1) time
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
If there are at most m jobs then

92. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Before we prove this, we prove another useful fact and a Lemma
Fact If there are at most m jobs (n m) then LPT is optimal
Lemma If n > m then Opt 2t(m+1) (after sorting)
LPT gives each job its own machine so maxi Li maxj tj Opt
◦ Note that t1 t2 t3 . . . tm t(m+1)
◦ One of the m machines must be assigned
• Let Tl denote the time taken by the LPT schedule
Proof
(at least) two of these m + 1 jobs under any schedule
◦ So we have that any schedule takes at least 2t(m+1) time
Li is the load of
machine i
m machines
n jobs
in particular Opt 2t(m+1)
Job j takes tj
time units
If there are at most m jobs then

93. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units

94. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
Proof Consider the machine i with largest load Tl = Li
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units

95. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units

96. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

97. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

98. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

99. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

100. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5
because LPT is optimal in this case

101. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

102. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

103. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5
Fact Opt maxj tj

104. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

105. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
so assume that (Li − tj) > 0
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

106. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
so assume that (Li − tj) > 0
• Therefore machine i was assigned at least two jobs
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

107. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
so assume that (Li − tj) > 0
• Therefore machine i was assigned at least two jobs
By the algorithm description, we have that j m + 1
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

108. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
so assume that (Li − tj) > 0
• Therefore machine i was assigned at least two jobs
By the algorithm description, we have that j m + 1
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5
it doesn’t assign a second job to any machine until
every machine has at least one job

109. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
so assume that (Li − tj) > 0
• Therefore machine i was assigned at least two jobs
By the algorithm description, we have that j m + 1
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

110. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
so assume that (Li − tj) > 0
• Therefore machine i was assigned at least two jobs
By the algorithm description, we have that j m + 1
tj tm+1 Opt/2 (by the Lemma)
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

111. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
so assume that (Li − tj) > 0
• Therefore machine i was assigned at least two jobs
By the algorithm description, we have that j m + 1
tj tm+1 Opt/2 (by the Lemma)
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5
Lemma If n > m then Opt 2t(m+1) (after sorting)

112. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
so assume that (Li − tj) > 0
• Therefore machine i was assigned at least two jobs
By the algorithm description, we have that j m + 1
tj tm+1 Opt/2 (by the Lemma)
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

113. The LPT approximation
Theorem The LPT algorithm is a 3/2-approximation algorithm
• Let j denote the last job machine i completes
Proof Consider the machine i with largest load Tl = Li
• Using the same argument as before, we have that,
(Li − tj) Opt
Therefore, Tl = Li = (Li − tj) + tj Opt + Opt/2 = (3/2) · Opt
• If n m then we are done so assume n > m
• Further if (Li − tj) = 0 then Tl = Li = tj Opt
so assume that (Li − tj) > 0
• Therefore machine i was assigned at least two jobs
By the algorithm description, we have that j m + 1
tj tm+1 Opt/2 (by the Lemma)
Li is the load of
machine i
m machines
n jobs
Job j takes tj
time units
job j
1
2
3
4
5

114. Scheduling conclusions
Theorem The LPT algorithm is a 3/2-approximation algorithm
which runs in O(n log n) time
Theorem The greedy algorithm is a 2-approximation algorithm
which runs in O(n log m) time and it’s online
In fact, LPT is a 4/3-approximation algorithm (using better analysis)
m machines
n jobs

115. k-centers

116. k-centers

117. k-centers
n points (sites) in 2D space

118. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2

119. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
(i.e. ‘normal’ euclidean distance)

120. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
Select k sites to be
centers
(i.e. ‘normal’ euclidean distance)

121. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
Select k sites to be
centers
(i.e. ‘normal’ euclidean distance)

122. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
Select k sites to be
centers

123. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
Goal Minimise the largest distance from any site to the closest center
Select k sites to be
centers

124. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
Goal Minimise the largest distance from any site to the closest center
Select k sites to be
centers

125. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
Goal Minimise the largest distance from any site to the closest center
Select k sites to be
centers
r
r

126. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
Goal Minimise the largest distance from any site to the closest center
Select k sites to be
centers

127. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
Goal Minimise the largest distance from any site to the closest center
Select k sites to be
centers

128. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
Goal Minimise the largest distance from any site to the closest center
Select k sites to be
centers
r

129. k-centers
n points (sites) in 2D space
The distance between points si, sj is (xi − xj)2 + (yi − yj)2
Goal Minimise the largest distance from any site to the closest center
(in general it’s NP-hard)
Select k sites to be
centers
r

130. A Greedy approximation

131. Start by picking any point to be a center
A Greedy approximation

132. Start by picking any point to be a center
A Greedy approximation

133. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

134. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

135. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

136. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

137. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

138. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

139. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

140. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

141. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

142. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

143. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

144. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

145. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

146. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation

147. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
A Greedy approximation
r

148. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
This takes O(nk) time
A Greedy approximation

149. Start by picking any point to be a center
Repeatedly pick the site which is furthest from any existing center
This takes O(nk) time
A Greedy approximation
but is it any good?

150. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)

151. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 1: No si, si ∈ Cg are closest to the same sj ∈ COpt

152. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 1: No si, si ∈ Cg are closest to the same sj ∈ COpt
Optimal centers

153. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 1: No si, si ∈ Cg are closest to the same sj ∈ COpt
Optimal centers
Opt

154. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 1: No si, si ∈ Cg are closest to the same sj ∈ COpt
Optimal centers
Opt
Sites

155. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 1: No si, si ∈ Cg are closest to the same sj ∈ COpt
Optimal centers
Opt
Sites
purposes only
Disclaimer: for illustrative

156. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 1: No si, si ∈ Cg are closest to the same sj ∈ COpt
Optimal centers
Opt
Sites
purposes only
Disclaimer: for illustrative
Greedy centers

157. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 1: No si, si ∈ Cg are closest to the same sj ∈ COpt
Optimal centers
Opt
Sites
purposes only
Disclaimer: for illustrative
Greedy centers

158. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 1: No si, si ∈ Cg are closest to the same sj ∈ COpt
Optimal centers
Opt
Sites
purposes only
Disclaimer: for illustrative
Greedy centers
Distance at most 2Opt

159. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 1: No si, si ∈ Cg are closest to the same sj ∈ COpt
Optimal centers
Opt
Sites
purposes only
Disclaimer: for illustrative
Greedy centers
Distance at most 2Opt
so rg 2Opt

160. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 2: Some si, si ∈ Cg are closest to the same sj ∈ COpt

161. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 2: Some si, si ∈ Cg are closest to the same sj ∈ COpt
si
si

162. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 2: Some si, si ∈ Cg are closest to the same sj ∈ COpt
Assume wlog. that Greedy made si a center after si
si
si

163. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 2: Some si, si ∈ Cg are closest to the same sj ∈ COpt
Assume wlog. that Greedy made si a center after si
si
si
si was added as a center because it was

164. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 2: Some si, si ∈ Cg are closest to the same sj ∈ COpt
Assume wlog. that Greedy made si a center after si
si
si
si was added as a center because it was
the furthest from any existing Greedy center

165. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 2: Some si, si ∈ Cg are closest to the same sj ∈ COpt
Assume wlog. that Greedy made si a center after si
si
si
si was added as a center because it was
the furthest from any existing Greedy center
However, si is at most 2Opt away from si

166. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 2: Some si, si ∈ Cg are closest to the same sj ∈ COpt
Assume wlog. that Greedy made si a center after si
si
si
si was added as a center because it was
the furthest from any existing Greedy center
However, si is at most 2Opt away from si

167. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 2: Some si, si ∈ Cg are closest to the same sj ∈ COpt
Assume wlog. that Greedy made si a center after si
si
si
si was added as a center because it was
the furthest from any existing Greedy center
However, si is at most 2Opt away from si
So even before adding si as a center, all sites
were 2Opt away from a Greedy center

168. The Greedy approximation
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
Let Cg (resp. COpt) denote the set of centers selected by Greedy (resp. Optimal)
Proof
Let rg (resp. Opt) denote largest site-center distance using Greedy (resp. Optimal)
Case 2: Some si, si ∈ Cg are closest to the same sj ∈ COpt
Assume wlog. that Greedy made si a center after si
si
si
si was added as a center because it was
the furthest from any existing Greedy center
However, si is at most 2Opt away from si
So even before adding si as a center, all sites
were 2Opt away from a Greedy center
Therefore, rg 2Opt

169. k-center Conclusions
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
which runs in O(nk) time

170. k-center Conclusions
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
which runs in O(nk) time
• The approximation works for any (metric) distance function,

171. k-center Conclusions
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
which runs in O(nk) time
• The approximation works for any (metric) distance function,
d(si, sj) = L1 or L∞ for example

172. k-center Conclusions
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
which runs in O(nk) time
• The approximation works for any (metric) distance function,
d(si, sj) = L1 or L∞ for example
d(x, y) = d(y, x), d(x, y) 0
• Distance function d is a metric iff
(d(x, y) = 0 iff x = y) and d(x, z) d(x, y) + d(y, z)

173. k-center Conclusions
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
which runs in O(nk) time
• The approximation works for any (metric) distance function,
d(si, sj) = L1 or L∞ for example
• For a general (metric) d, the problem is not α-approximable with α < 2
d(x, y) = d(y, x), d(x, y) 0
• Distance function d is a metric iff
(d(x, y) = 0 iff x = y) and d(x, z) d(x, y) + d(y, z)

174. k-center Conclusions
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
which runs in O(nk) time
• The approximation works for any (metric) distance function,
d(si, sj) = L1 or L∞ for example
• For a general (metric) d, the problem is not α-approximable with α < 2
d(x, y) = d(y, x), d(x, y) 0
• For d = L2 , the problem is not α-approximable with α <
√
3 ≈ 1.73
• Distance function d is a metric iff
(d(x, y) = 0 iff x = y) and d(x, z) d(x, y) + d(y, z)

175. k-center Conclusions
Theorem The Greedy algorithm for k-center is a 2-approximation algorithm
which runs in O(nk) time
• The approximation works for any (metric) distance function,
d(si, sj) = L1 or L∞ for example
• For a general (metric) d, the problem is not α-approximable with α < 2
d(x, y) = d(y, x), d(x, y) 0
• For d = L2 , the problem is not α-approximable with α <
√
3 ≈ 1.73
• For d = L1 or d = L∞ , the problem is not α-approximable with α < 2
• Distance function d is a metric iff
(d(x, y) = 0 iff x = y) and d(x, z) d(x, y) + d(y, z)