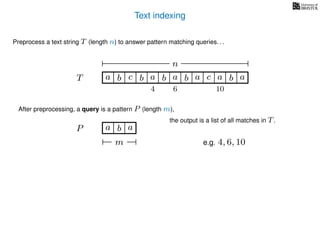
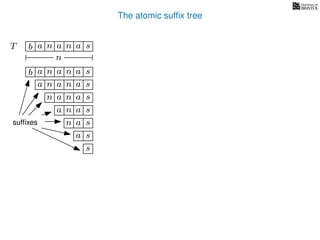
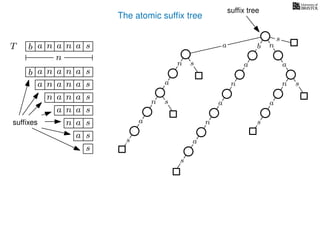
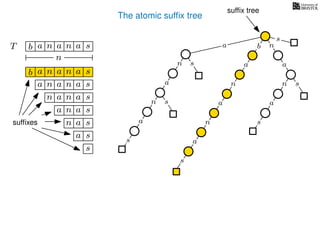
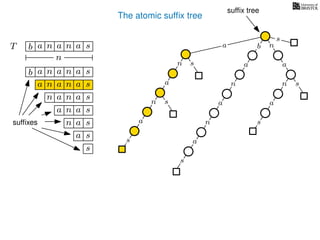
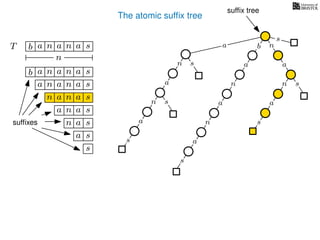
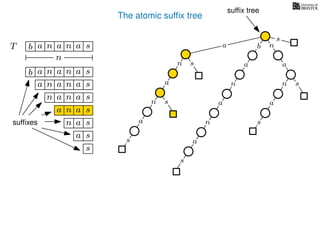
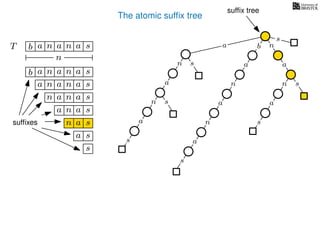
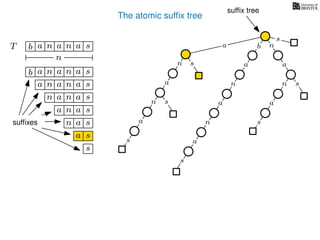
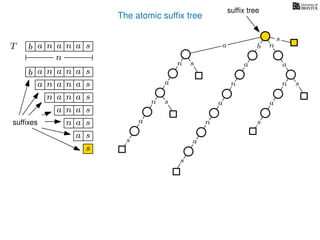
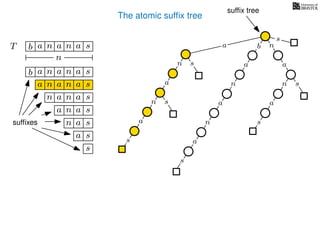
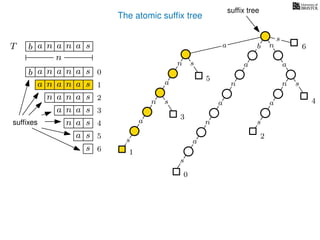
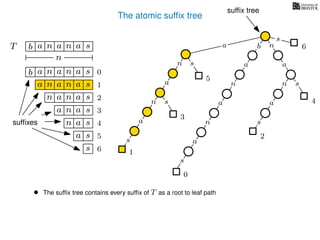
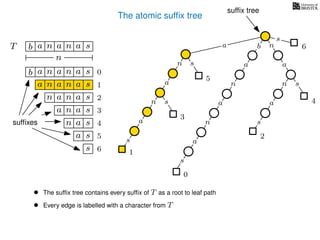
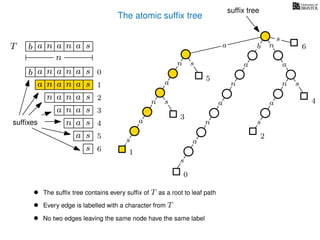
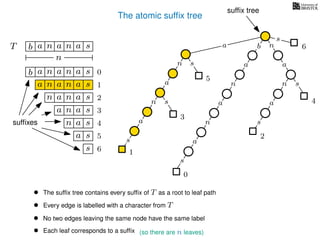
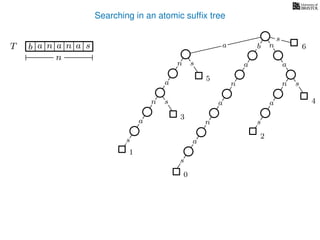
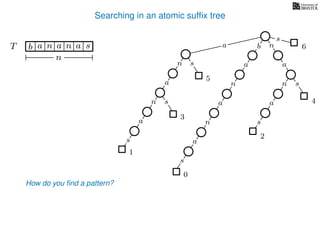
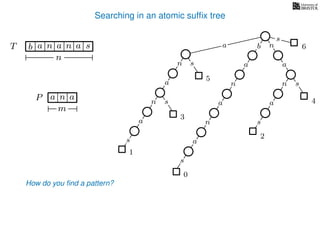
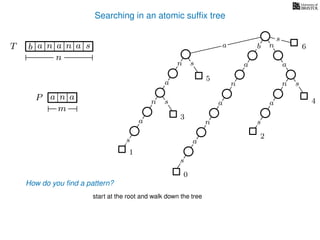
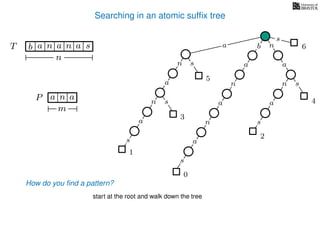
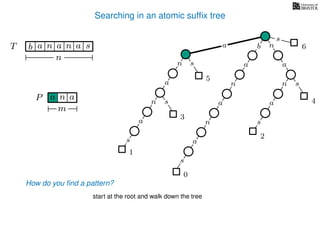
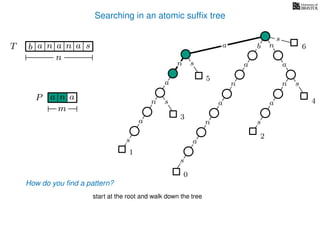
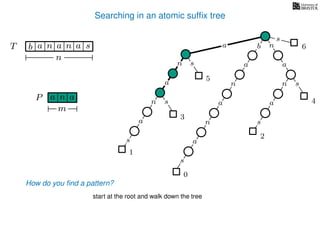
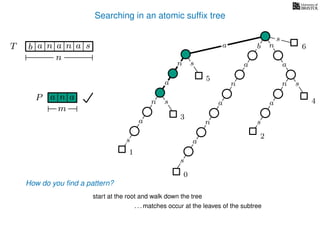
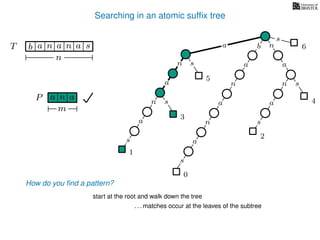
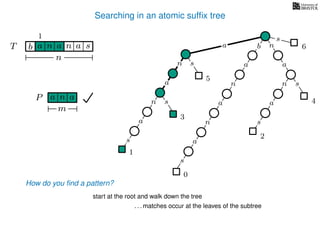
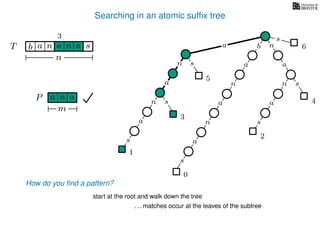
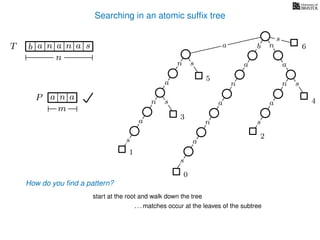
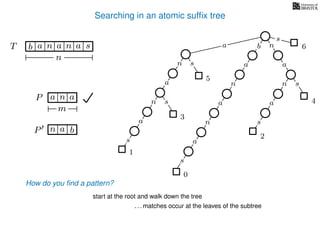
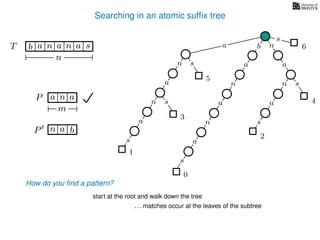
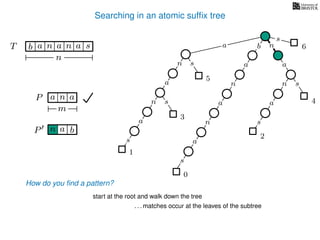
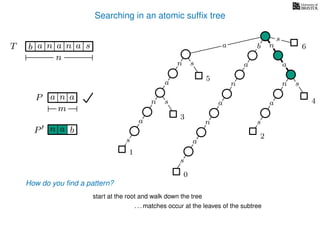
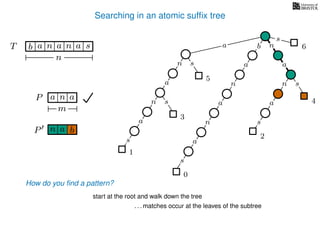
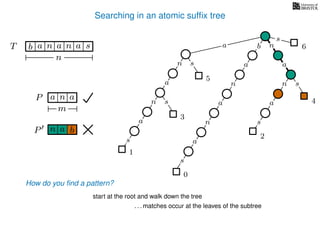
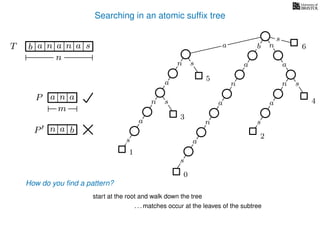
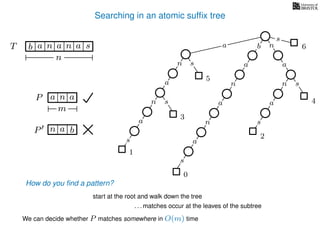
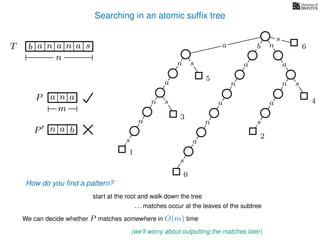
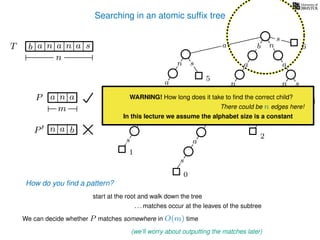
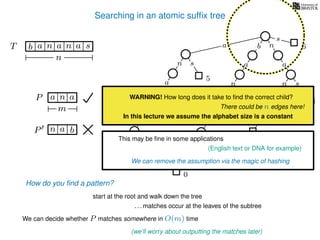
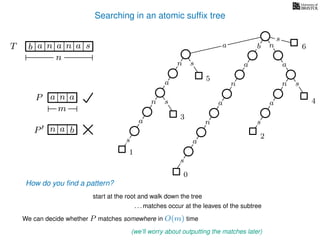
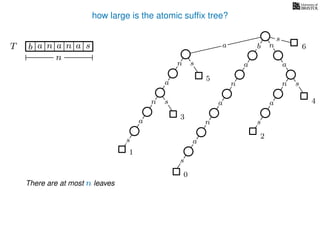
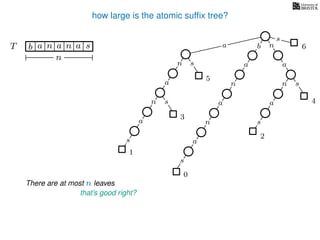
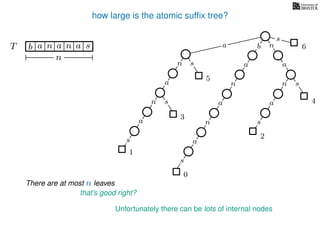
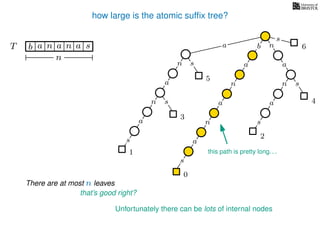
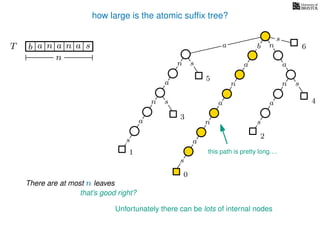
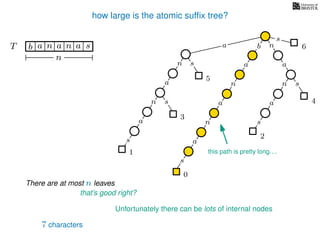
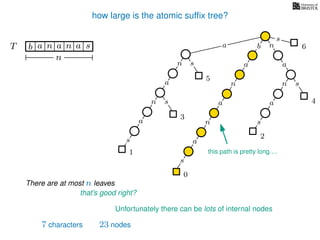
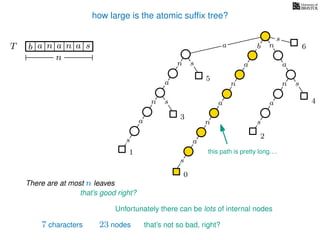
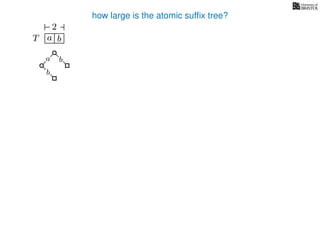
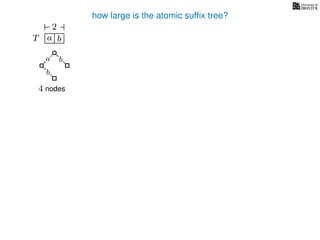
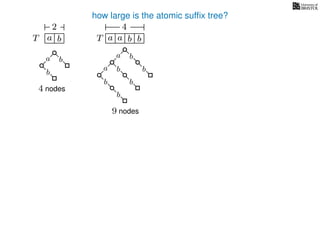
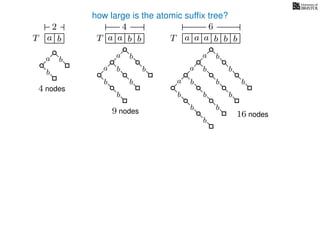
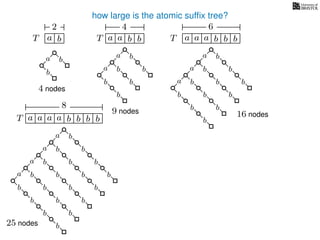
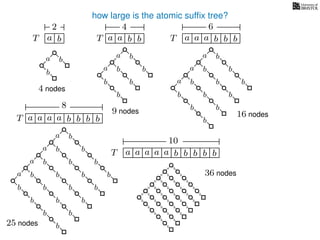
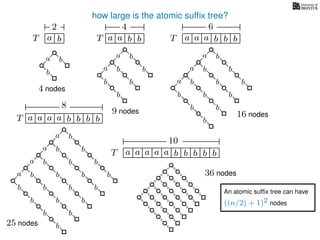
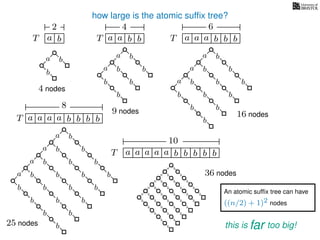
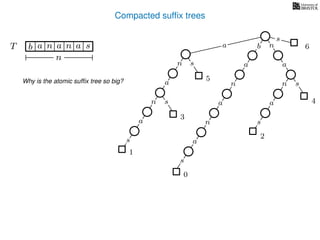
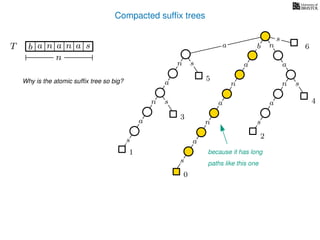
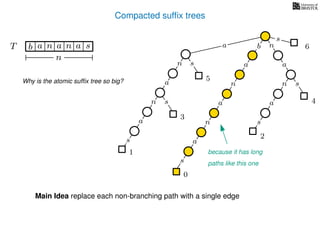
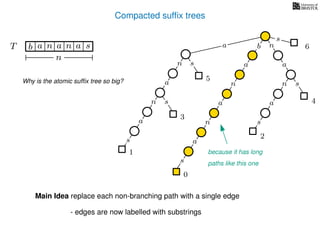
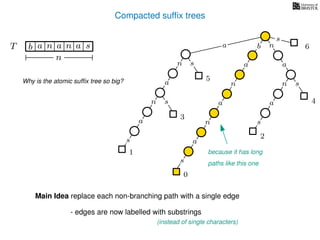
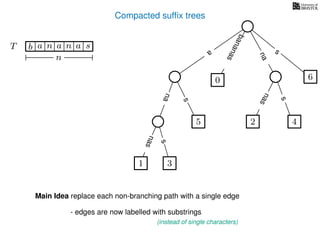
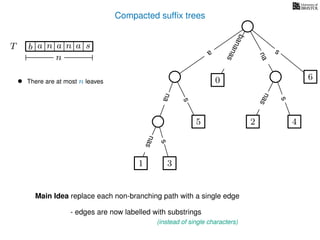
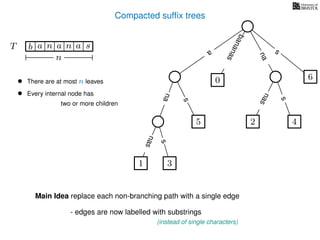
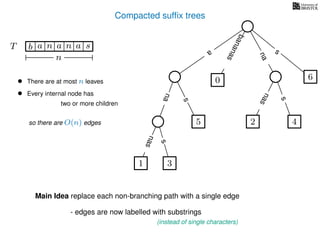
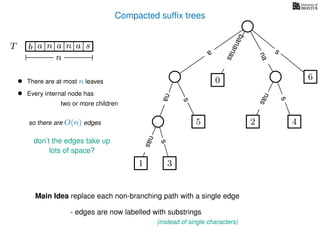
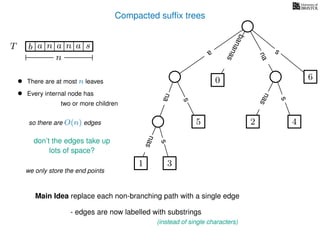
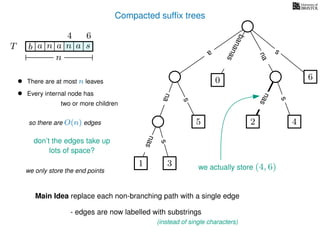
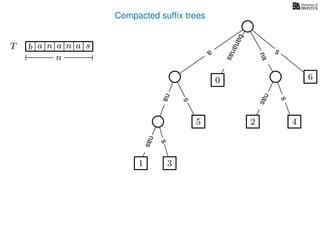
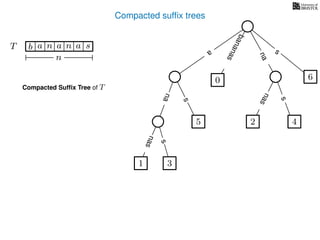
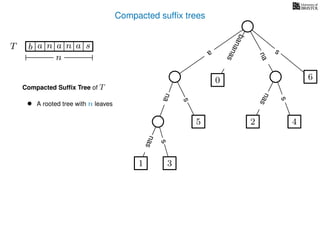
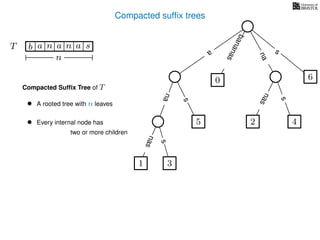
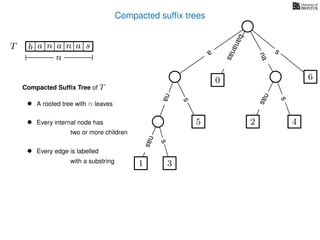
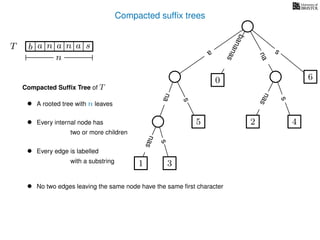
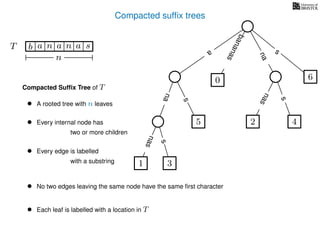
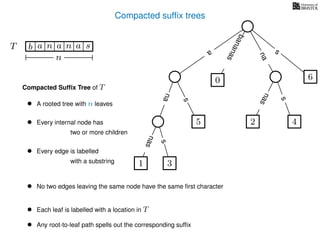
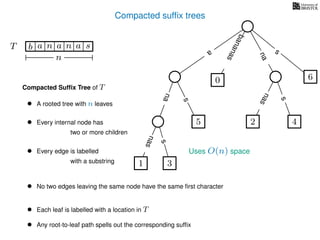
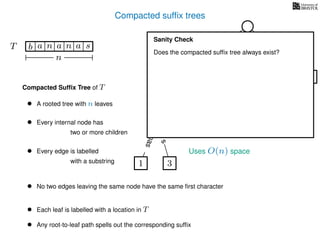
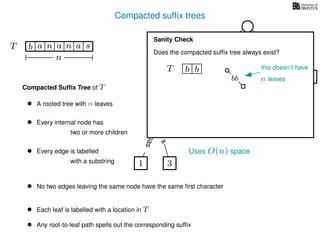
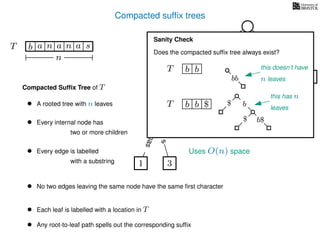
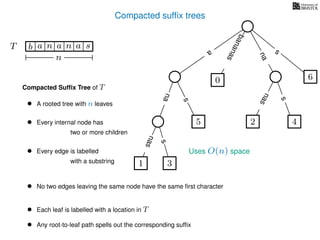
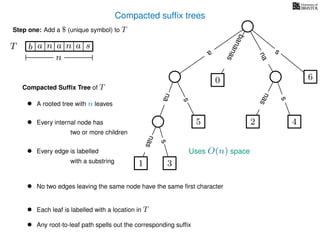
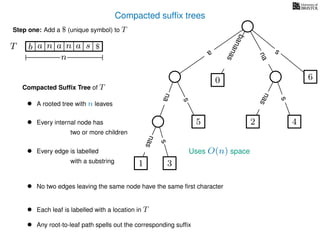
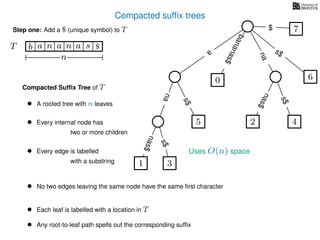
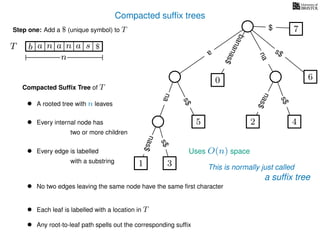
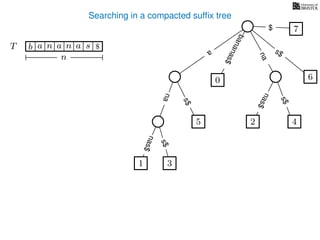
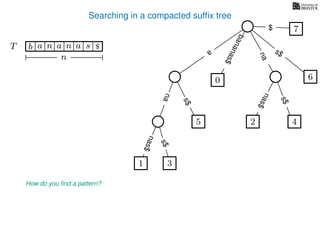
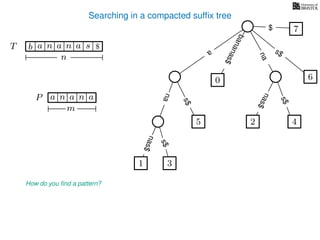
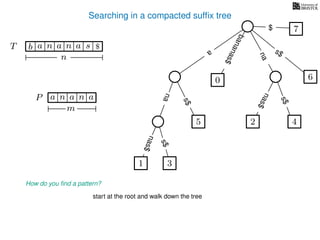
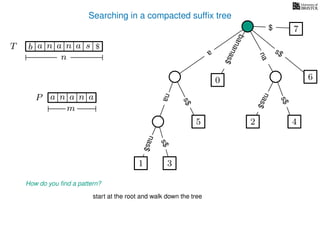
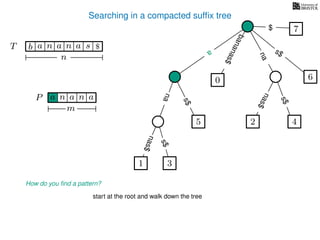
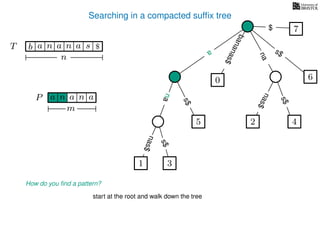
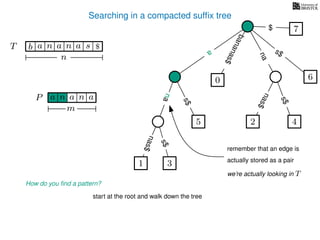
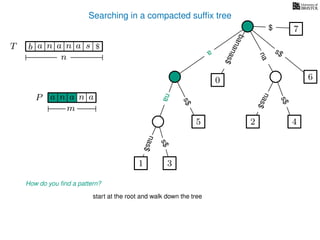
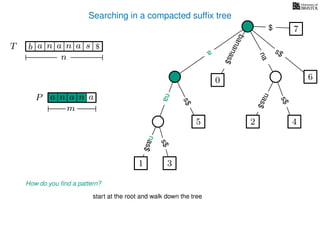
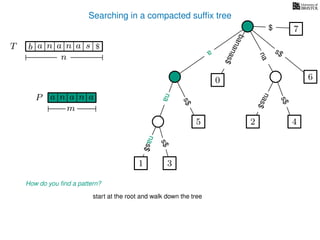
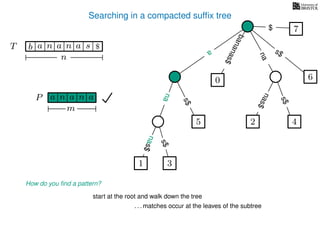
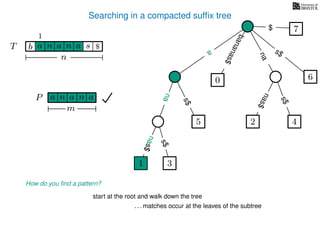
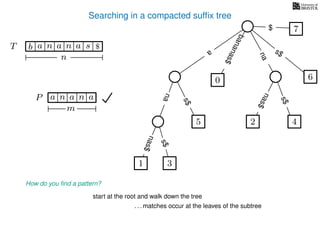
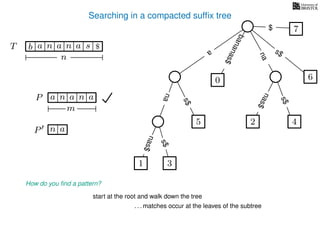
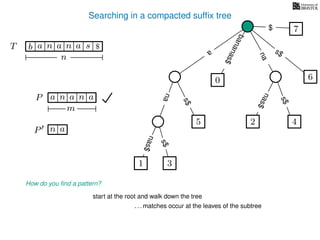
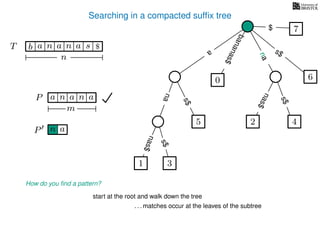
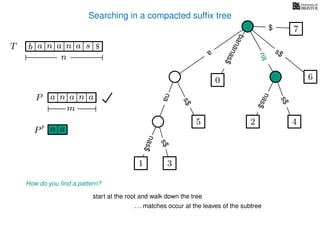
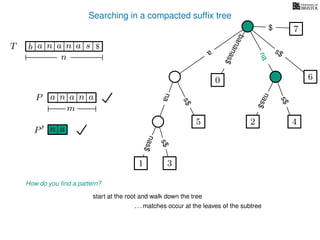
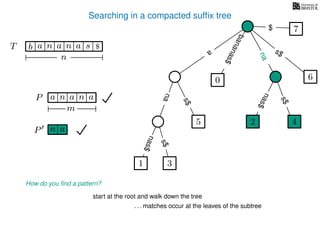
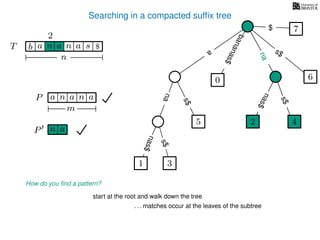
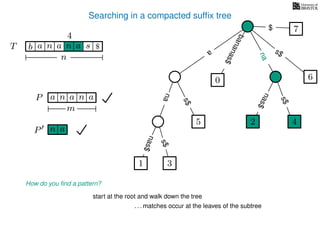
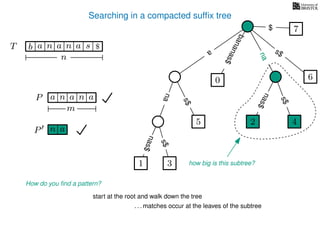
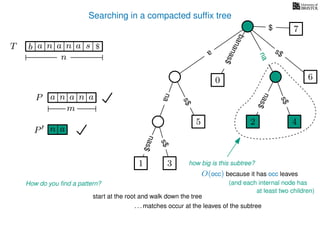
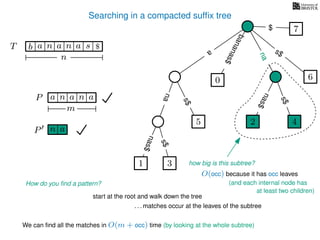
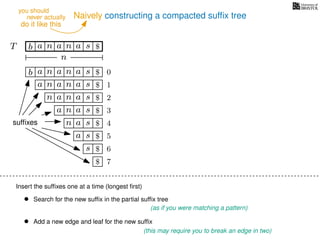
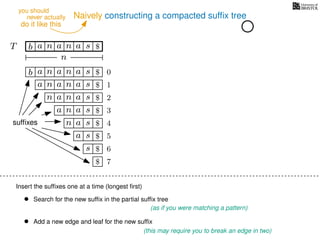
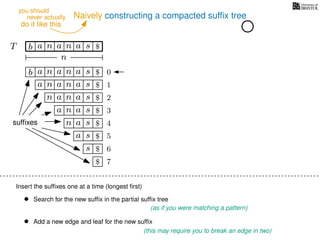
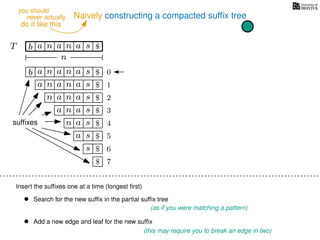
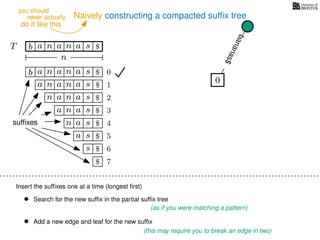
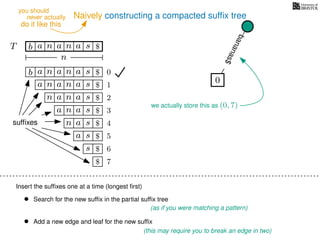
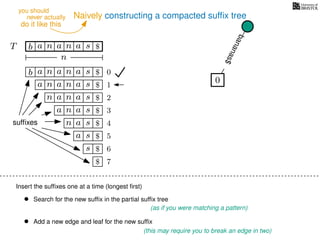
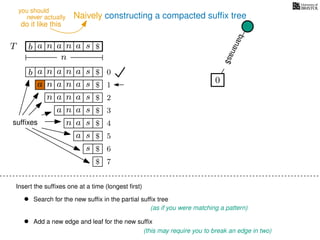
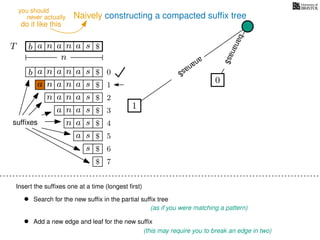
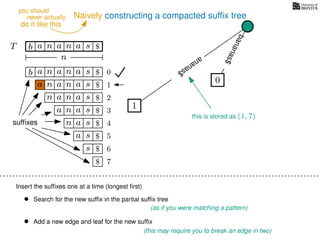
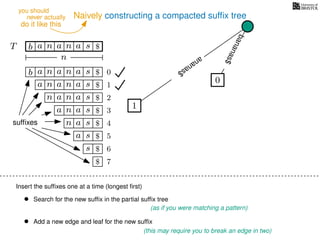
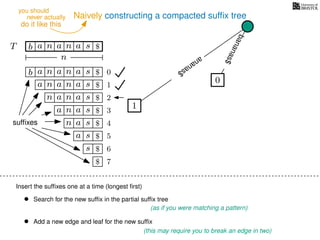
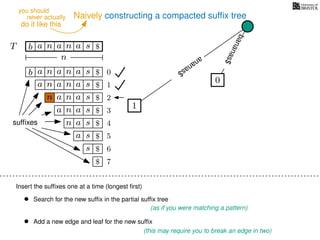
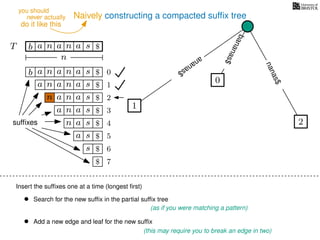
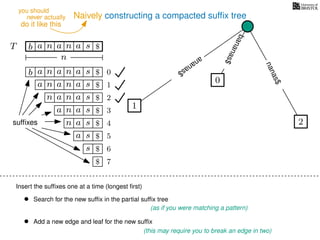
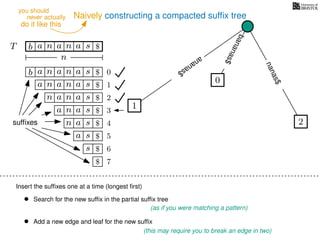
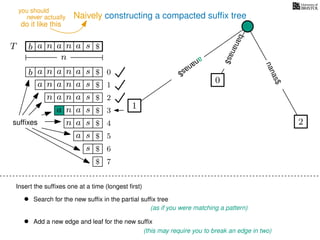
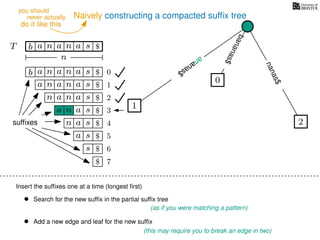
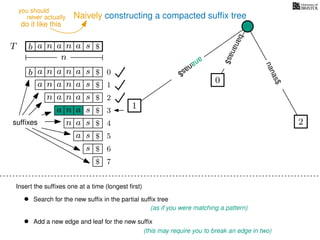
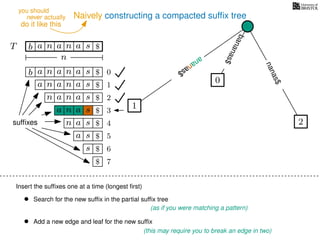
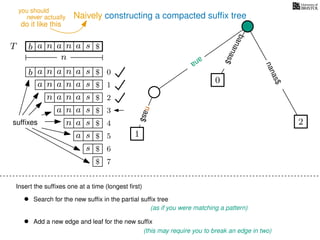
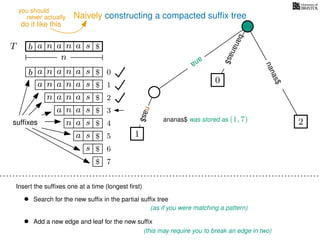
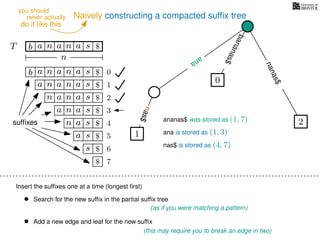
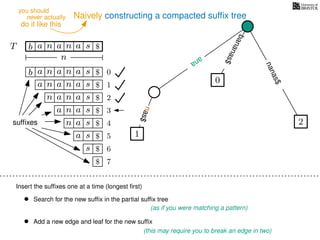
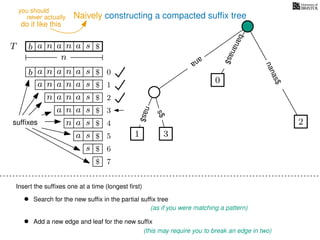
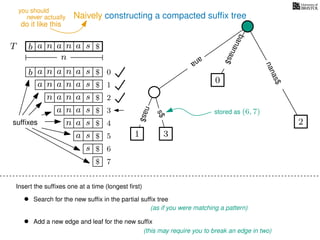
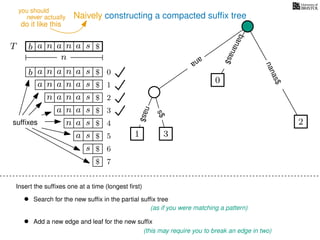
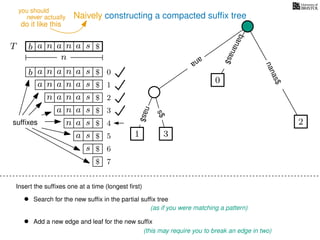
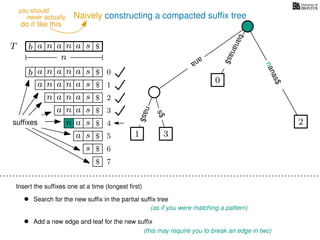
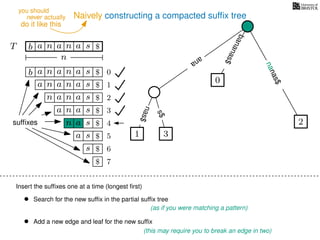
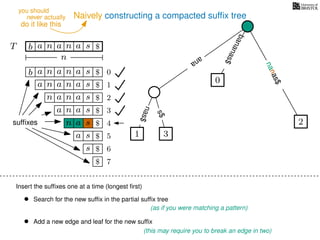
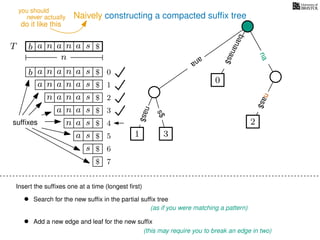
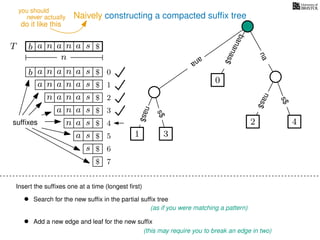
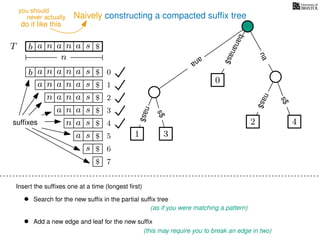
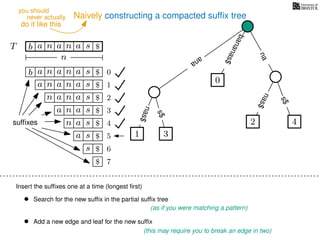
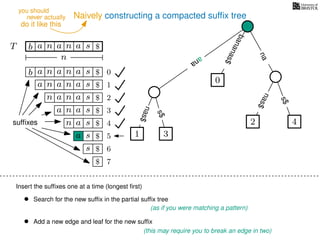
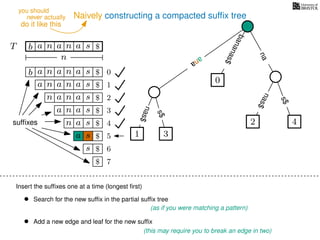
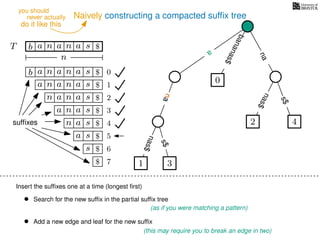
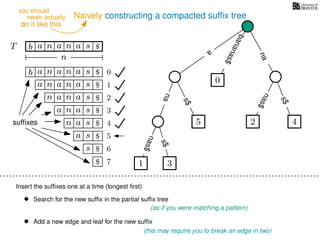
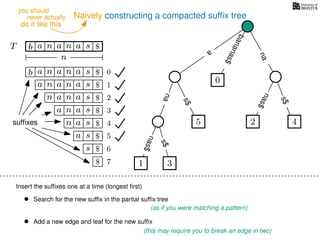
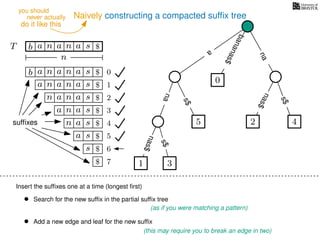
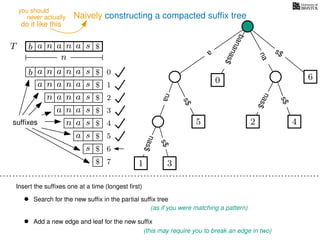
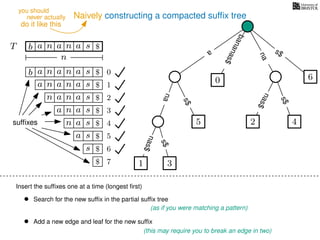
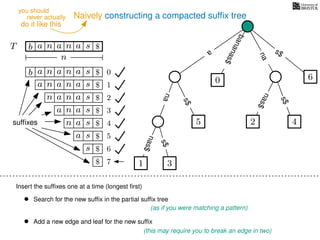
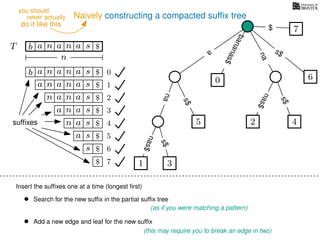
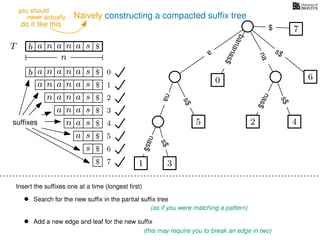
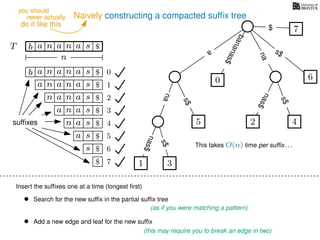
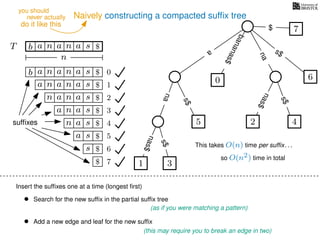
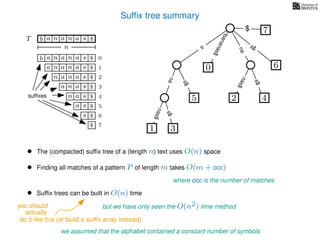
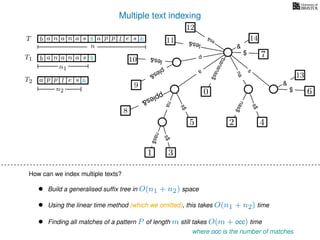
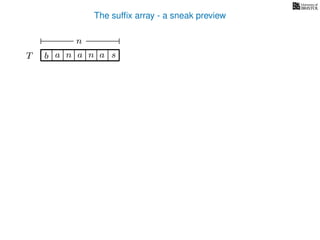
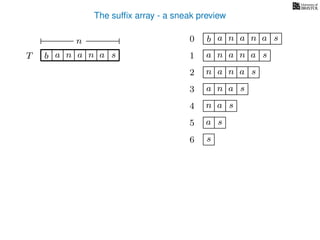
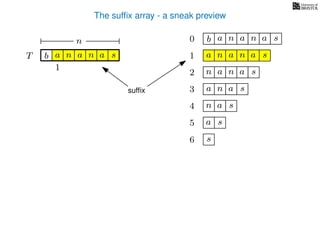
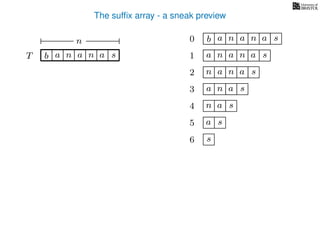
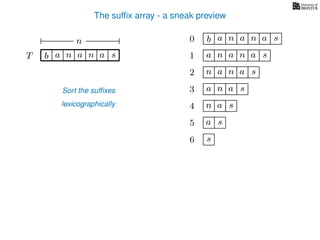
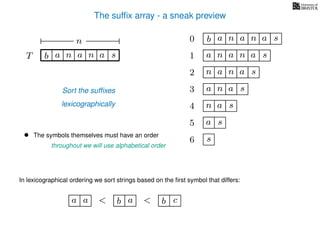
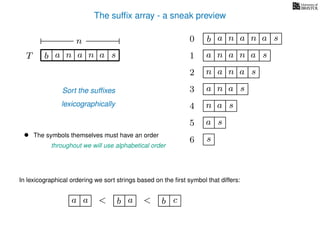
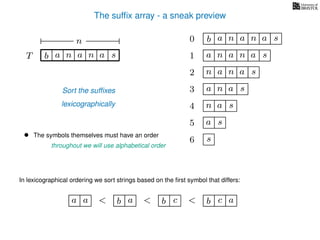
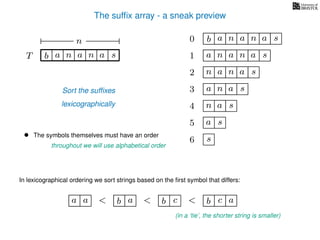
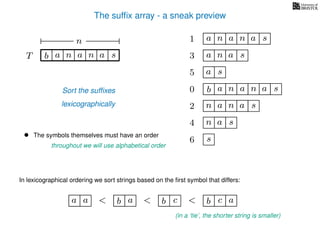
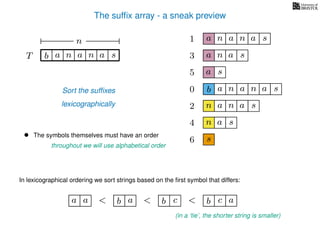
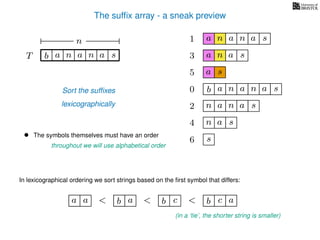
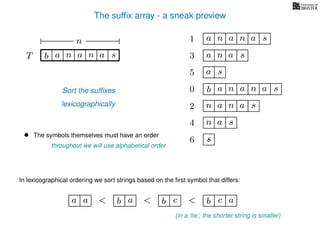
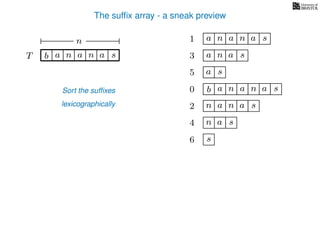
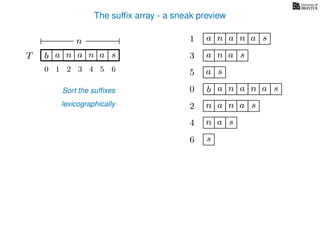
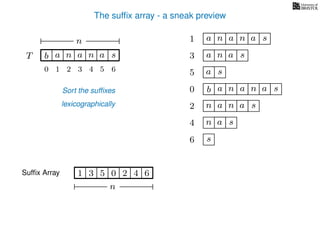
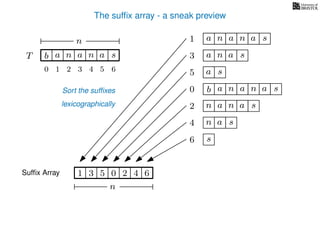
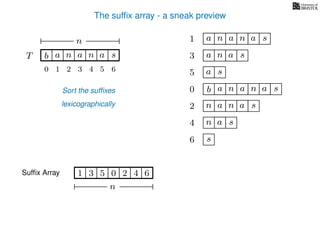
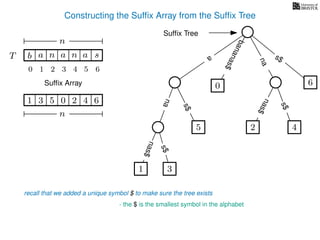
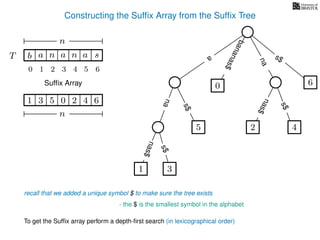
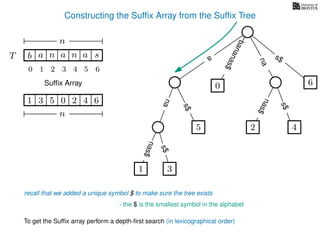
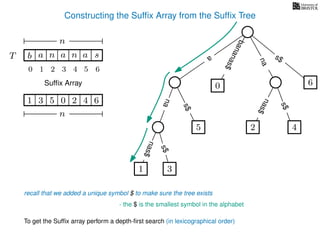
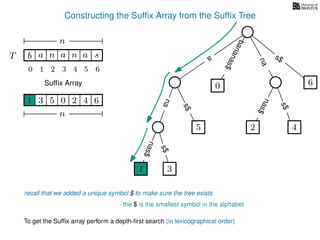
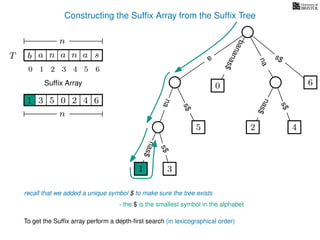
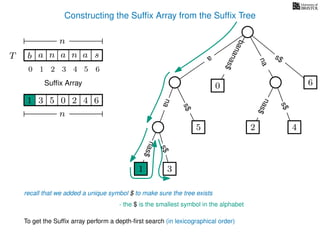
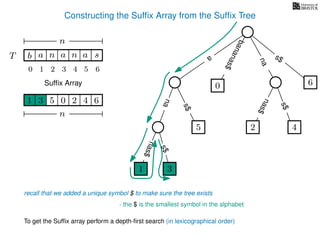
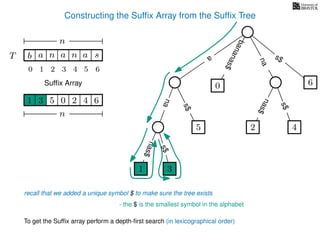
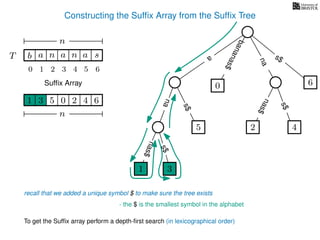
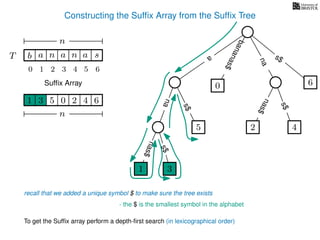
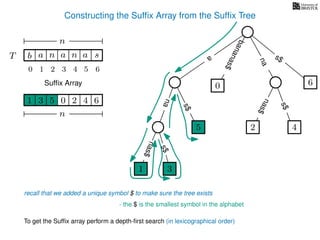
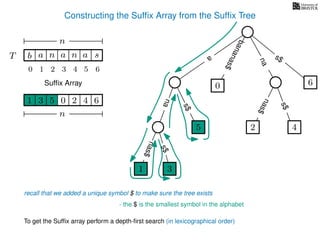
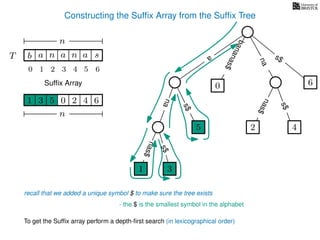
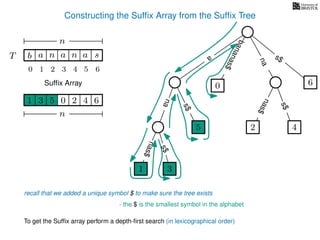
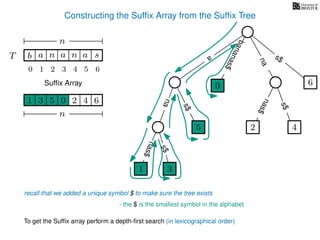
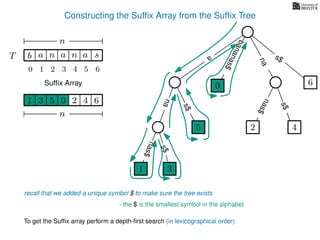
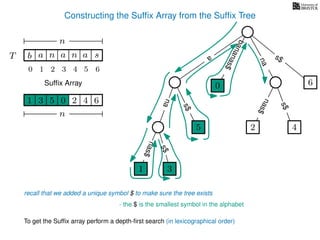
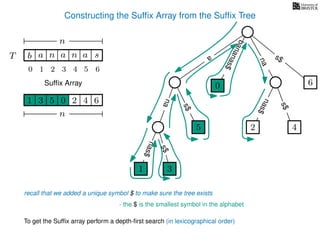
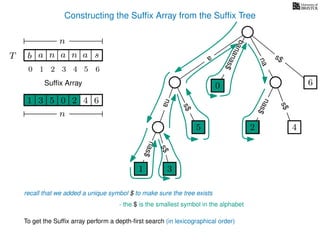
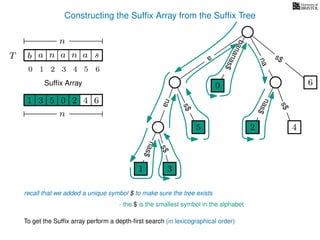
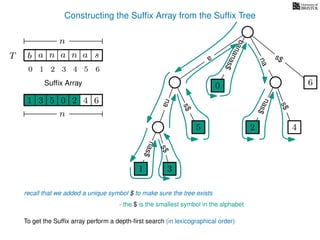
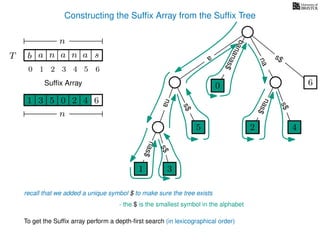
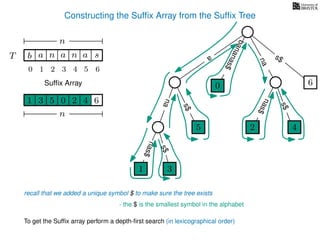
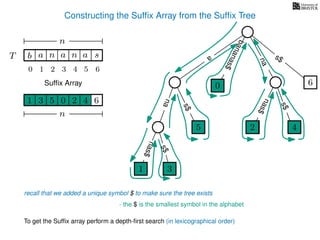
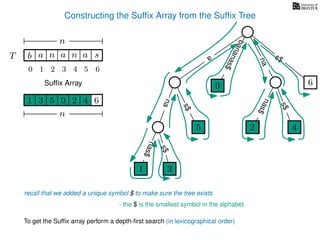
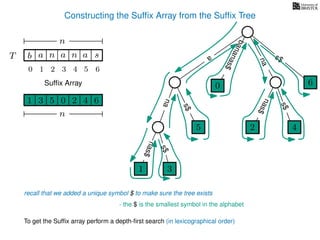
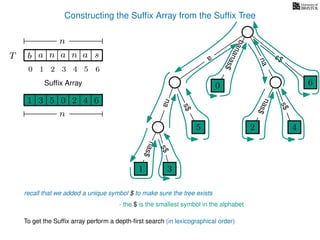
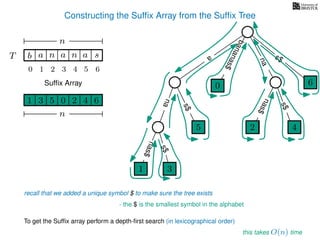
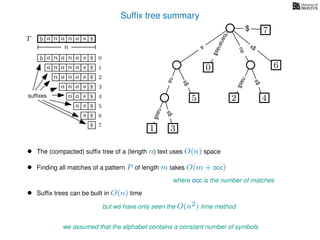
The document discusses exact pattern matching in strings using algorithms for finding matches between a pattern and a text string, highlighting the naive algorithm's O(nm) time complexity and introducing more efficient O(n) algorithms like KMP. It explains the concept of text indexing, where a text is preprocessed to facilitate quick pattern matching queries, and presents the structure and properties of suffix trees for efficient searching. Suffix trees allow for the representation of all suffixes of a string in a way that supports fast pattern searching, with each edge labeled by a character from the string.

![Exact pattern matching
T
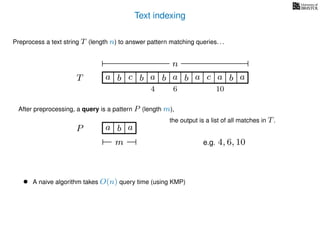
Input A text string T (length n) and a pattern string P (length m)
P
ba b c
a b a
a b a cb a
Goal: Find all the locations where P matches in T
P matches at location i iff
a b a
n
m
for all 0 j m we have that P[j] = T[i + j]
(our strings are zero-indexed)](https://image.slidesharecdn.com/aa-05-160916143737/85/Pattern-Matching-Part-One-Suffix-Trees-2-320.jpg)
![Exact pattern matching
T
Input A text string T (length n) and a pattern string P (length m)
P
ba b c
a b a
a b a cb a
Goal: Find all the locations where P matches in T
P matches at location i iff
a b a
n
m
4
for all 0 j m we have that P[j] = T[i + j]
(our strings are zero-indexed)](https://image.slidesharecdn.com/aa-05-160916143737/85/Pattern-Matching-Part-One-Suffix-Trees-3-320.jpg)
![Exact pattern matching
T
Input A text string T (length n) and a pattern string P (length m)
P
ba b c a b a cb a
Goal: Find all the locations where P matches in T
P matches at location i iff
a b a
n
a b a
m
6
for all 0 j m we have that P[j] = T[i + j]
(our strings are zero-indexed)](https://image.slidesharecdn.com/aa-05-160916143737/85/Pattern-Matching-Part-One-Suffix-Trees-4-320.jpg)
![Exact pattern matching
T
Input A text string T (length n) and a pattern string P (length m)
P
ba b c a b a cb a
Goal: Find all the locations where P matches in T
P matches at location i iff
a b a
n
a b a
m
10
for all 0 j m we have that P[j] = T[i + j]
(our strings are zero-indexed)](https://image.slidesharecdn.com/aa-05-160916143737/85/Pattern-Matching-Part-One-Suffix-Trees-5-320.jpg)
![Exact pattern matching
T
Input A text string T (length n) and a pattern string P (length m)
P
ba b c a b a cb a
Goal: Find all the locations where P matches in T
P matches at location i iff
a b a
n
a b a
m
6
for all 0 j m we have that P[j] = T[i + j]
(our strings are zero-indexed)](https://image.slidesharecdn.com/aa-05-160916143737/85/Pattern-Matching-Part-One-Suffix-Trees-6-320.jpg)
![Exact pattern matching
T
Input A text string T (length n) and a pattern string P (length m)
P
ba b c a b a cb a
Goal: Find all the locations where P matches in T
P matches at location i iff
a b a
n
a b a
m
6
for all 0 j m we have that P[j] = T[i + j]
(our strings are zero-indexed)
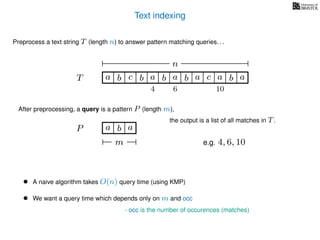
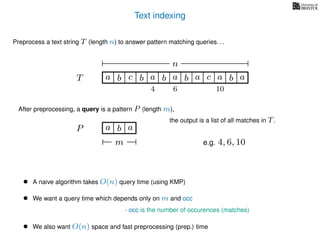
• A naive algorithm takes O(nm) time](https://image.slidesharecdn.com/aa-05-160916143737/85/Pattern-Matching-Part-One-Suffix-Trees-7-320.jpg)
![Exact pattern matching
T
Input A text string T (length n) and a pattern string P (length m)
P
ba b c a b a cb a
Goal: Find all the locations where P matches in T
P matches at location i iff
a b a
n
a b a
m
6
for all 0 j m we have that P[j] = T[i + j]
(our strings are zero-indexed)
• A naive algorithm takes O(nm) time
• Many O(n) time algorithms are known (for example KMP)](https://image.slidesharecdn.com/aa-05-160916143737/85/Pattern-Matching-Part-One-Suffix-Trees-8-320.jpg)