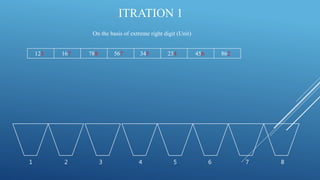
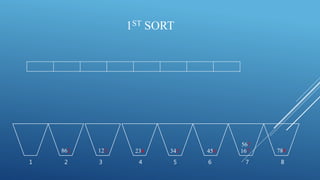
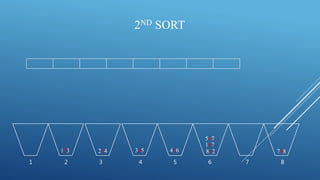
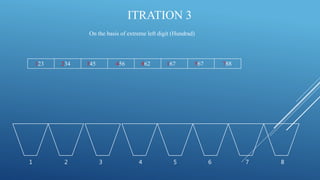
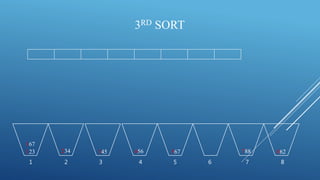
This document summarizes the radix sort algorithm in 3 steps: 1) It sorts the array by the rightmost digit (units place) then by the next digit to the left (tens place) and finally by the leftmost digit (hundreds place). 2) It provides an example of sorting the array [123, 167, 788, 567, 345, 234, 456, 862] in this way over 3 iterations. 3) After 3 iterations/sorts, the array is fully sorted from lowest to highest number.

1. DESIGN & ANALYSIS OF
ALGORITHMS
Radix sort
By: Zeeshan Ali
Roll No. : 9
BS(CS)

2. INTRODUCTION
 Very efficient for sorting a small array of integers
 Its time complexity is O (n)
 First we sort by digit in unit place
 Second we sort by digit in ten place
 Third we sort by digit in hundred place . . .

3. DRY RUN

4. STATEMENT
Lets take an array of integers: 123,167,788,567,345,234,456,862
i.e
123 167 788 567 345 234 456 862

5. ITRATION 1
123 167 788 567 345 234 456 862
1 2 3 4 5 6 7 8
On the basis of extreme right digit (Unit)

6. 1ST SORT
123 167 788
567
345234 456862
1 2 3 4 5 6 7 8

7. ITRATION 2
123 788567345234 456862
1 2 3 4 5 6 7 8
167
On the basis of middle digit (Ten)

8. 2ND SORT
123 788
567
345234 456 862
1 2 3 4 5 6 7 8
167

9. ITRATION 3
123 788567345234 456 862
1 2 3 4 5 6 7 8
167
On the basis of extreme left digit (Hundrad)

10. 3RD SORT
123 788567345234 456 862
1 2 3 4 5 6 7 8
167

11. SORTED ARRAY
123 167 234 345 456 567 788 862

12. THE END