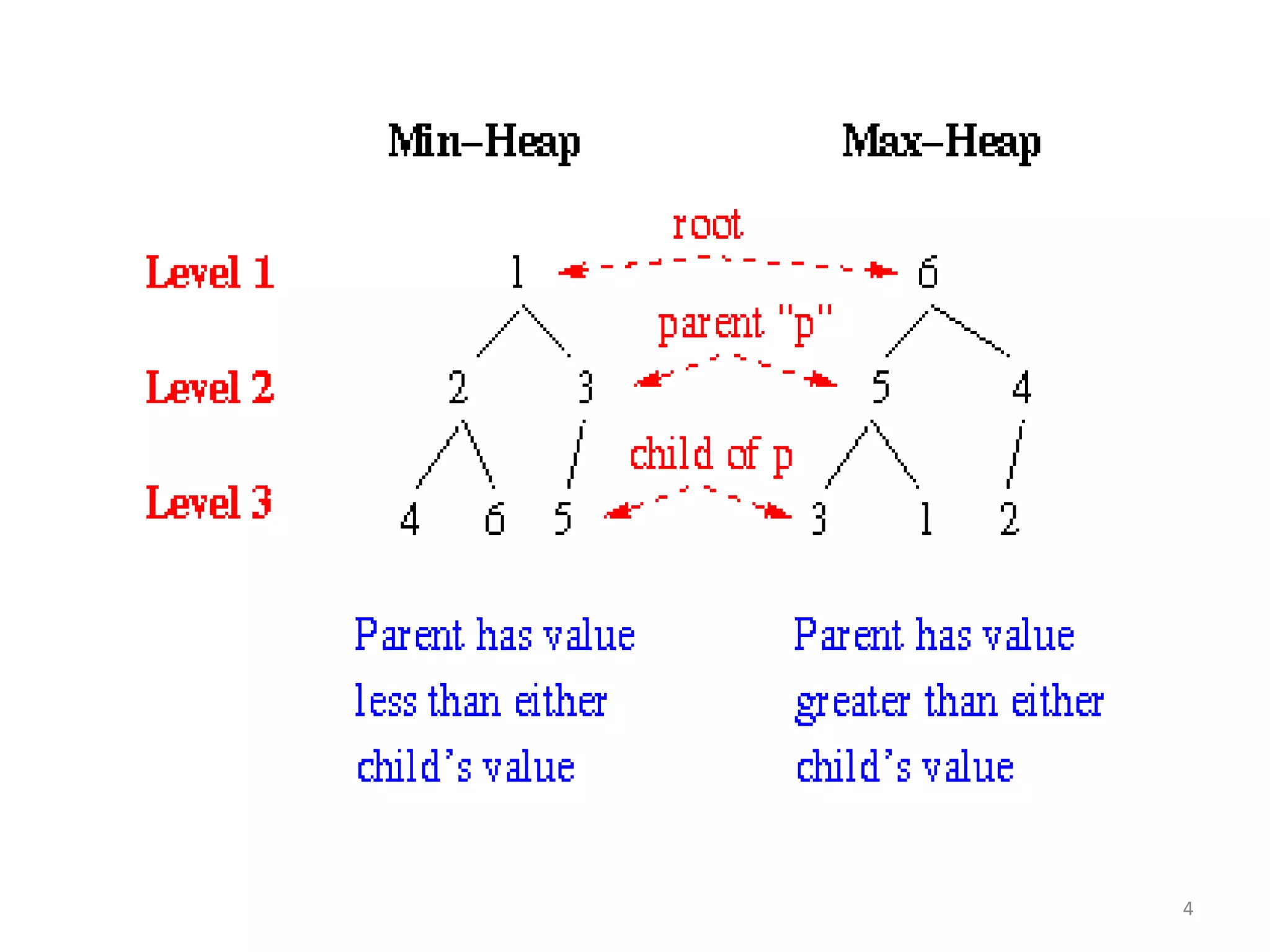
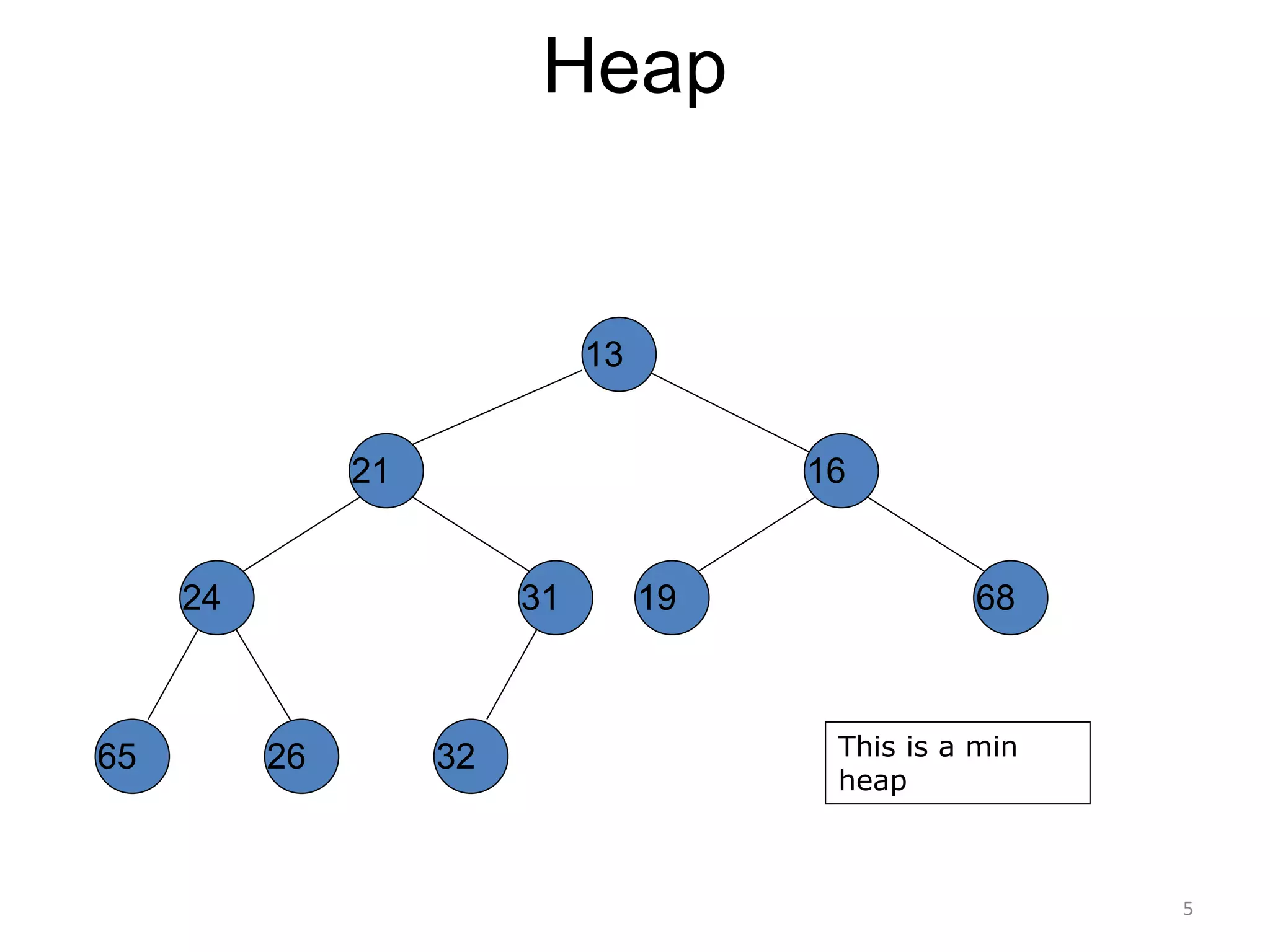
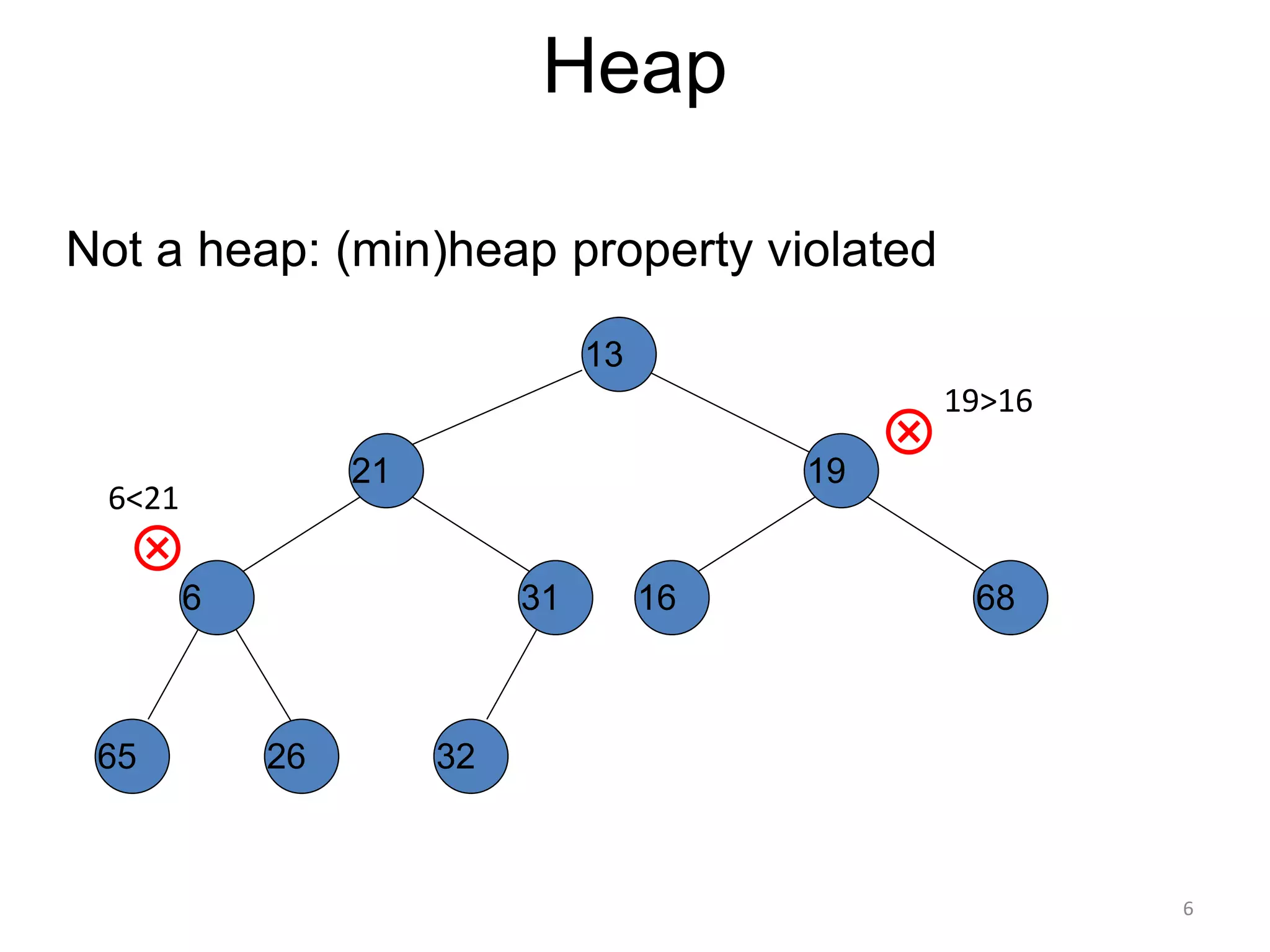
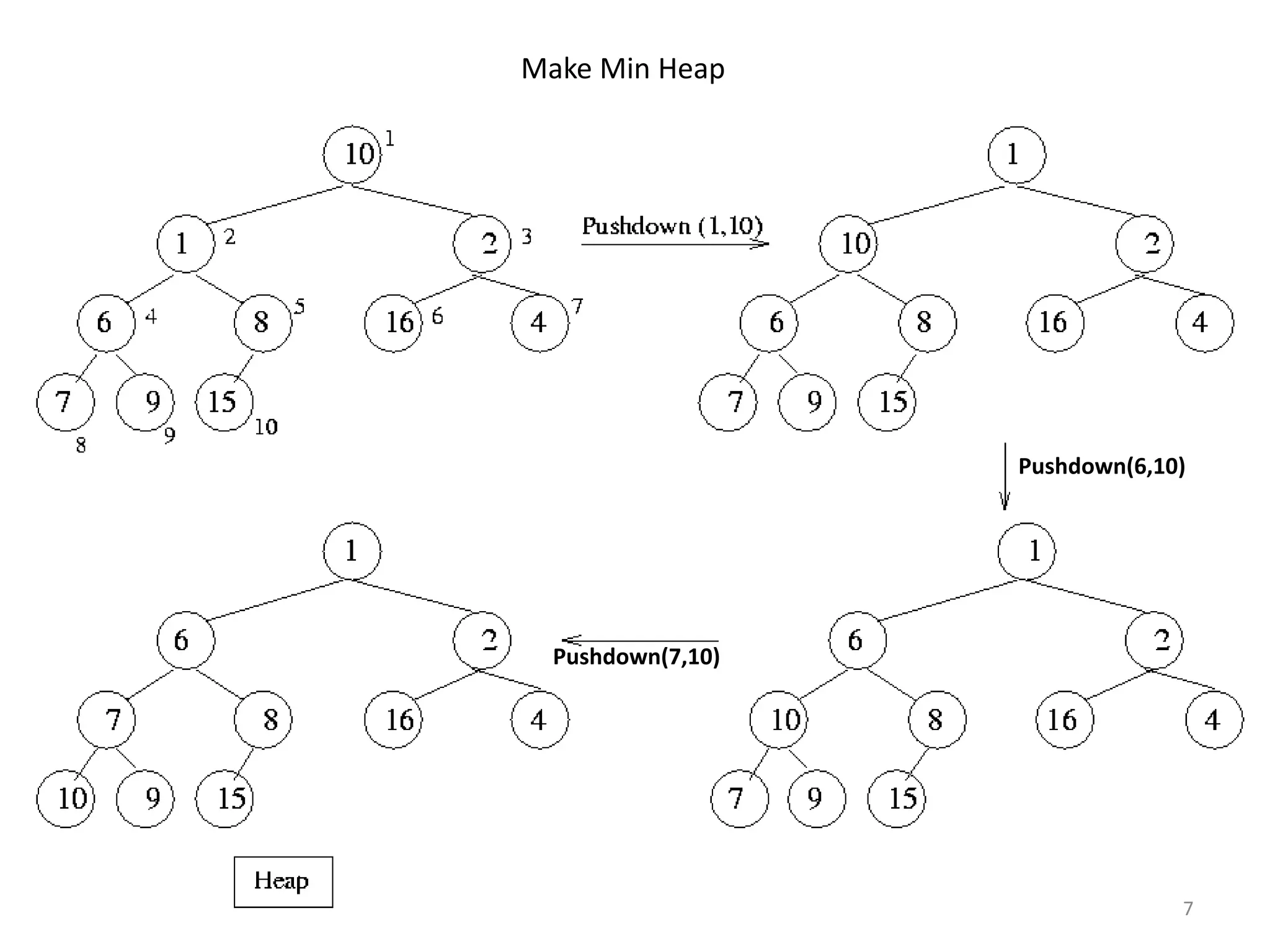
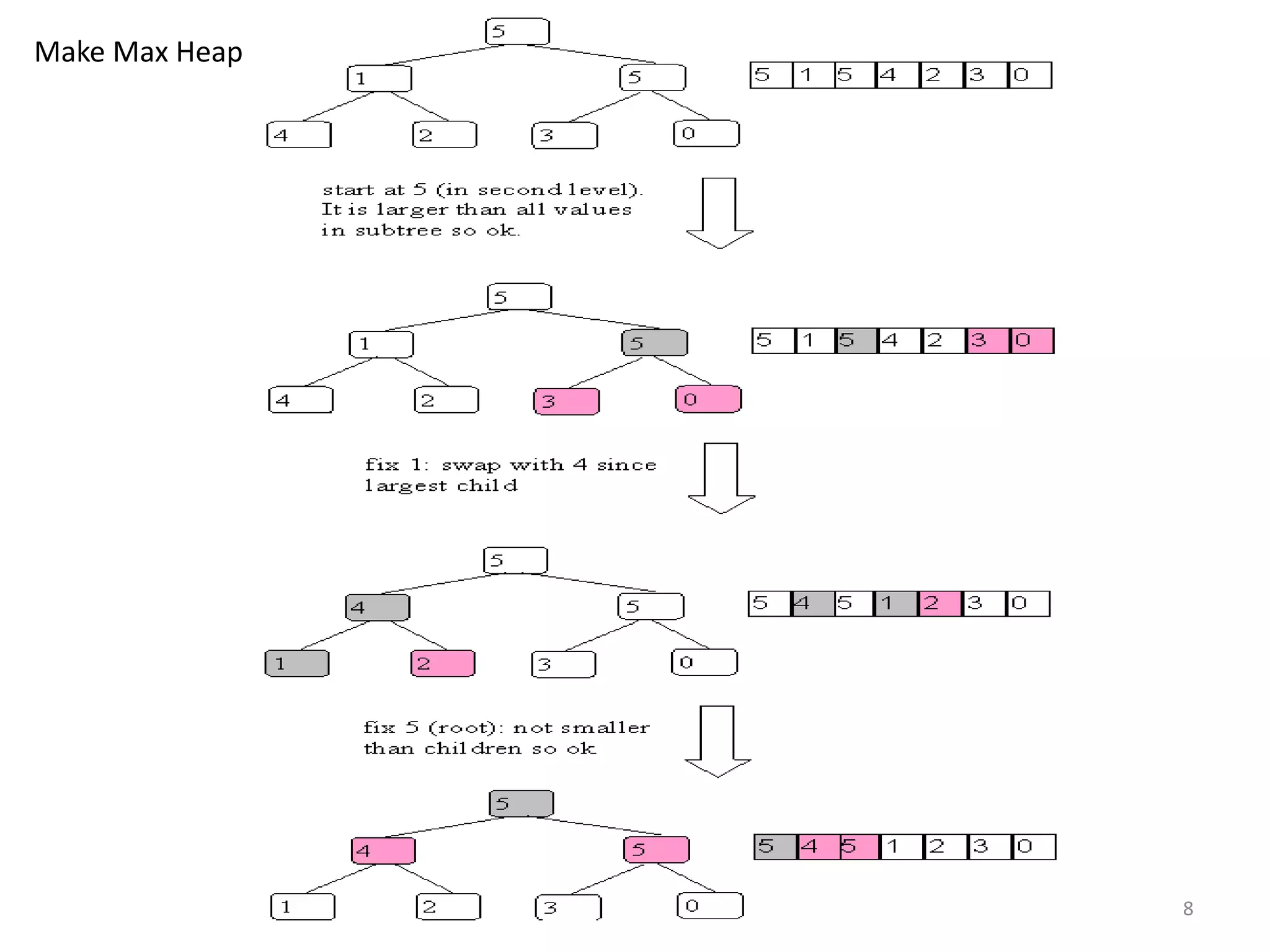
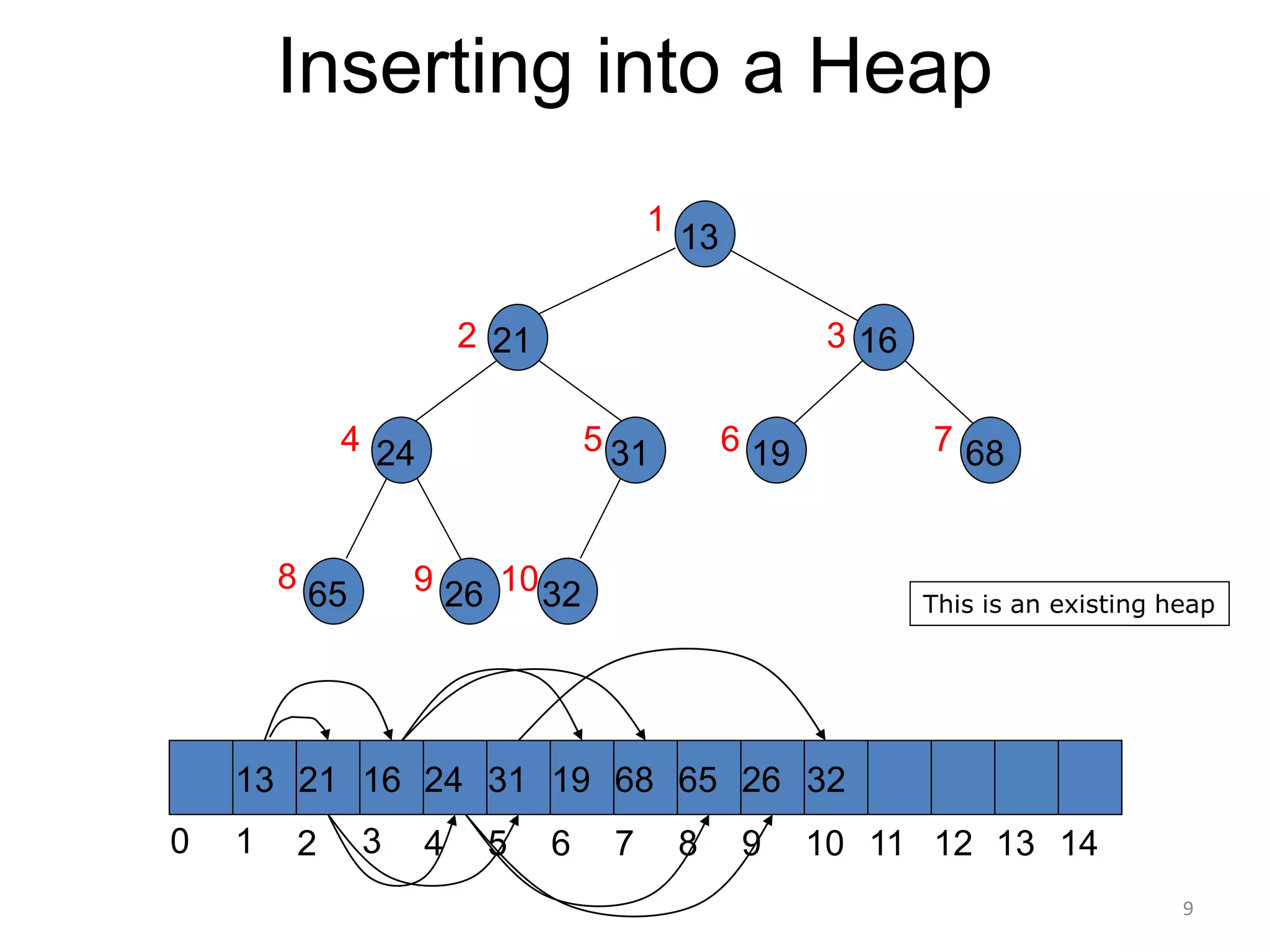
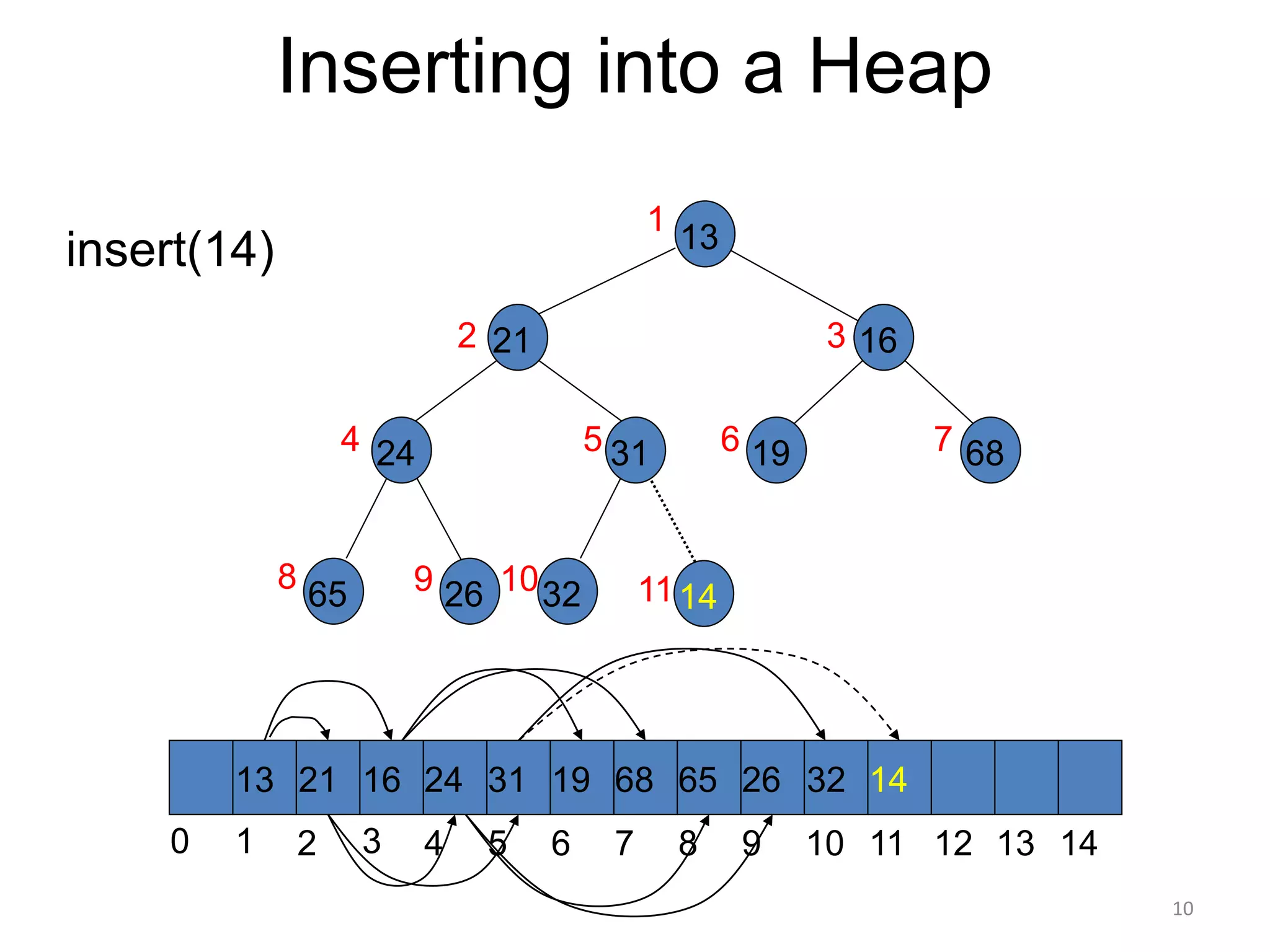
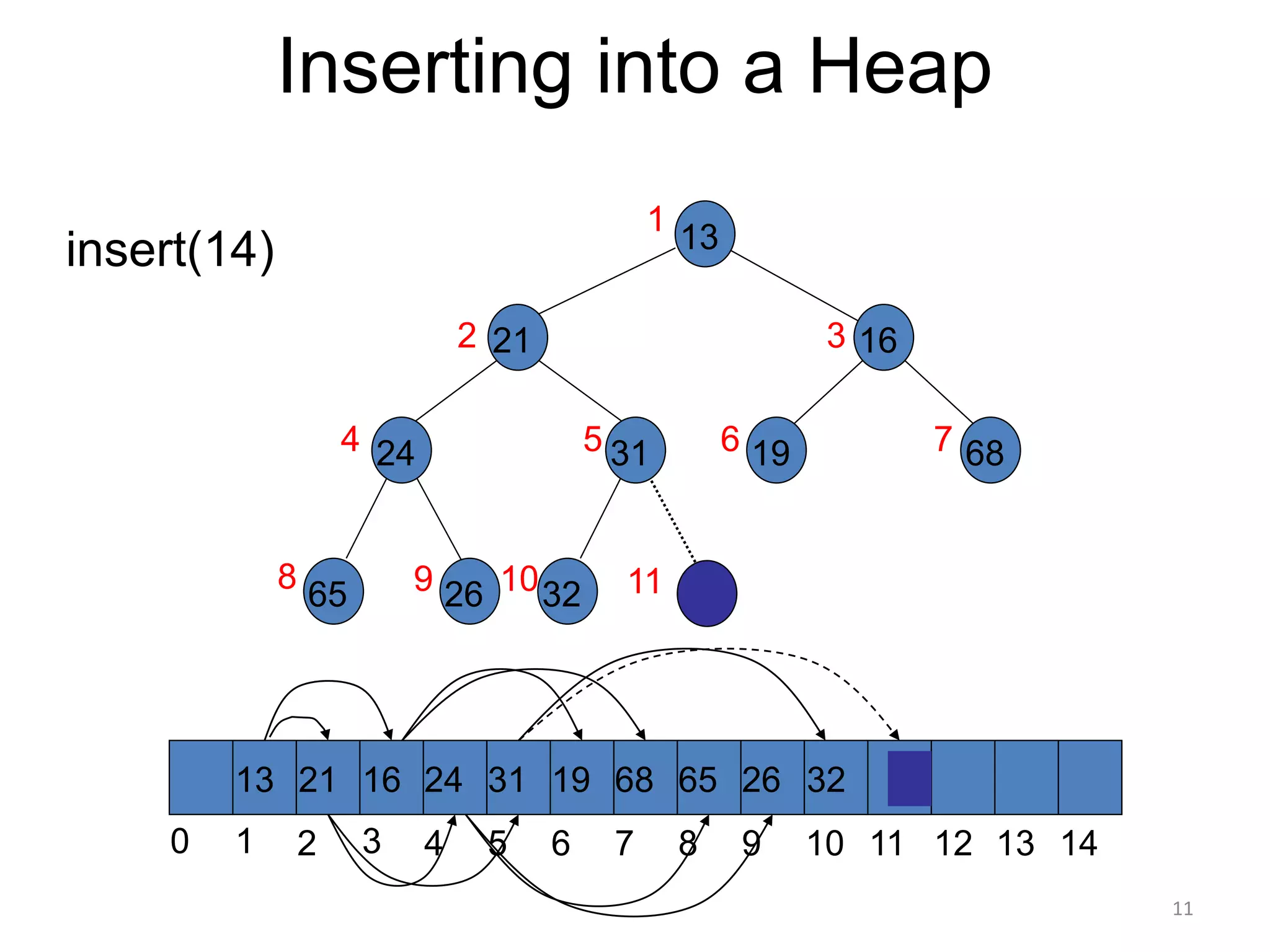
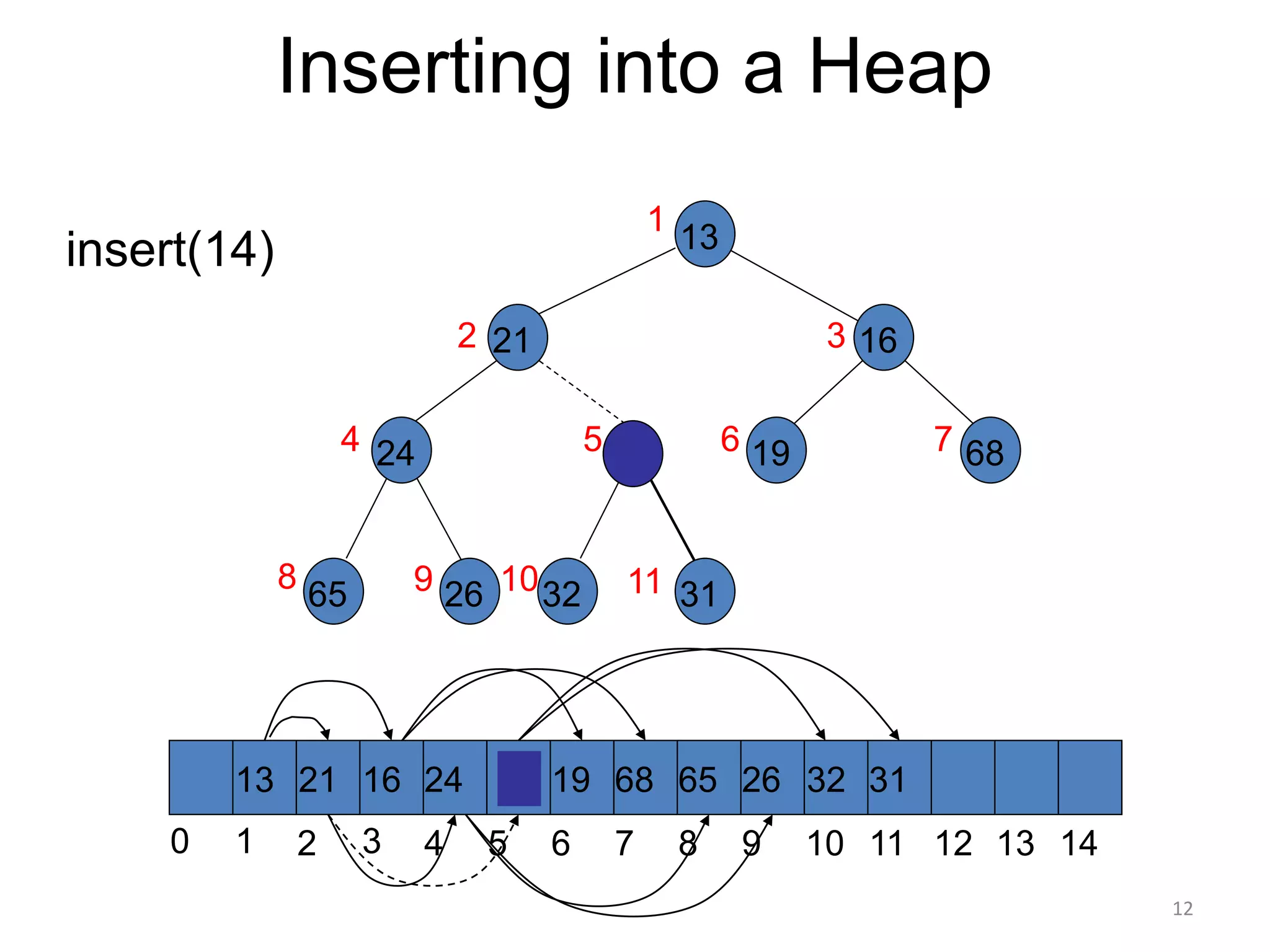
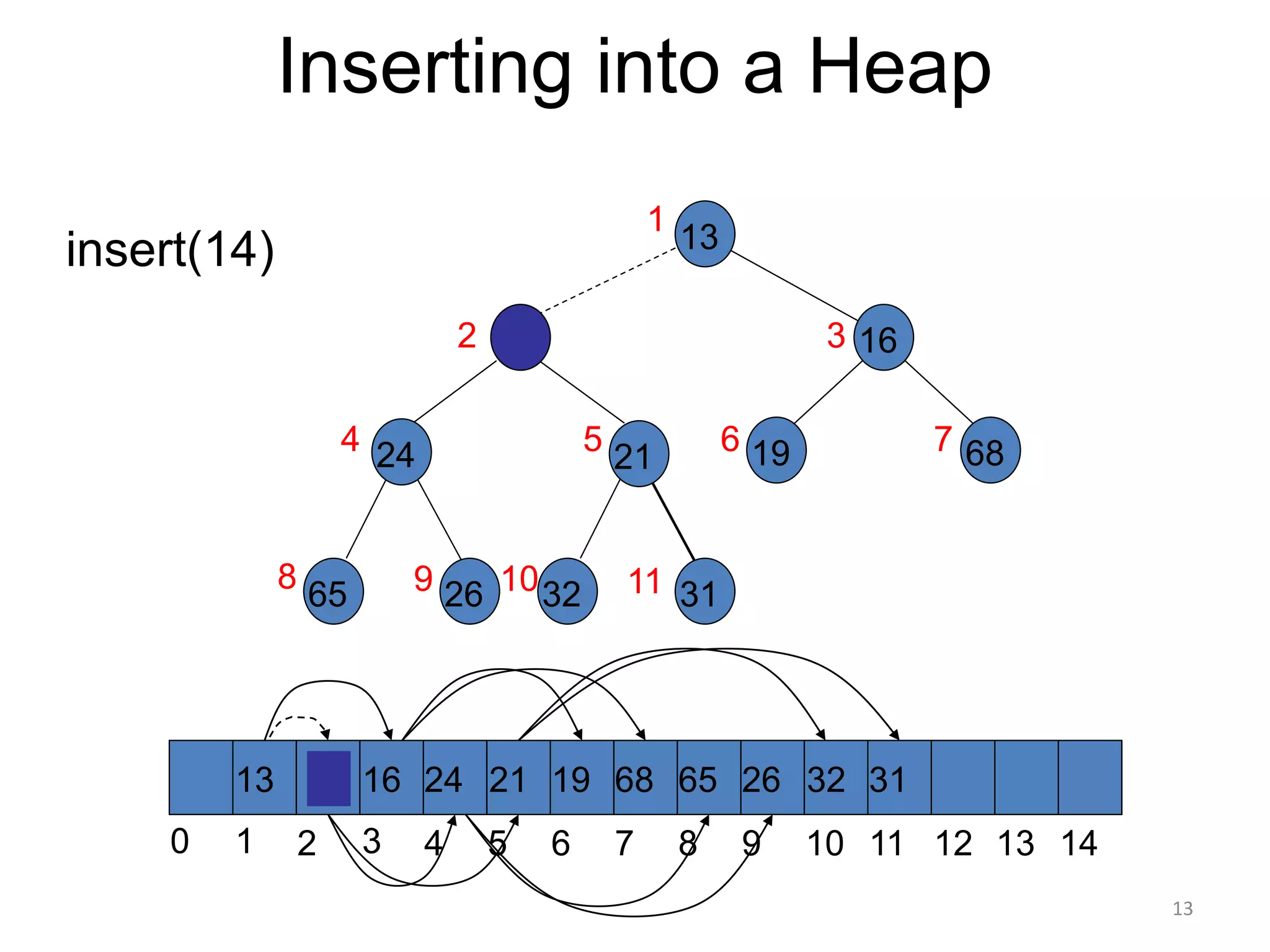
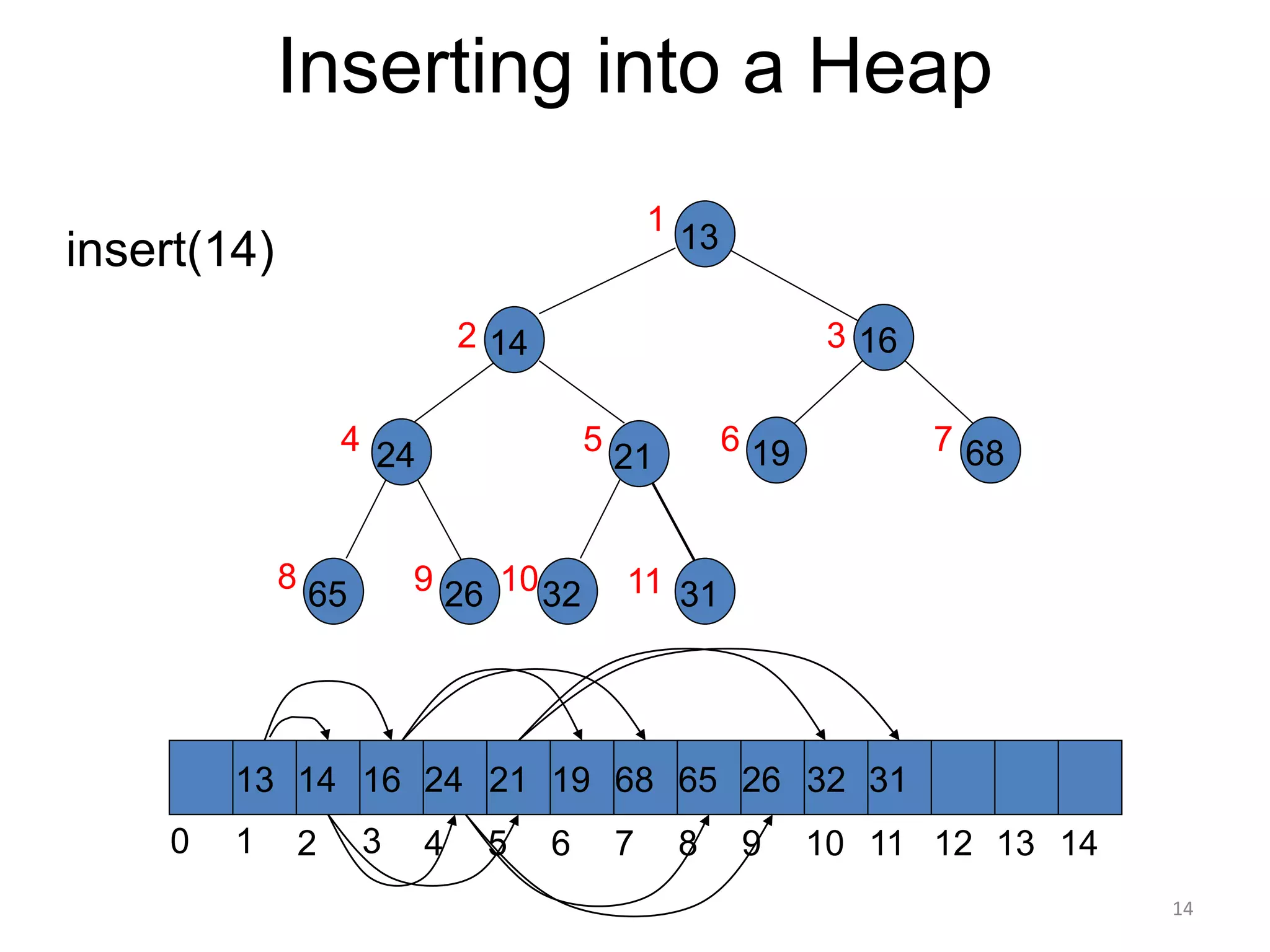
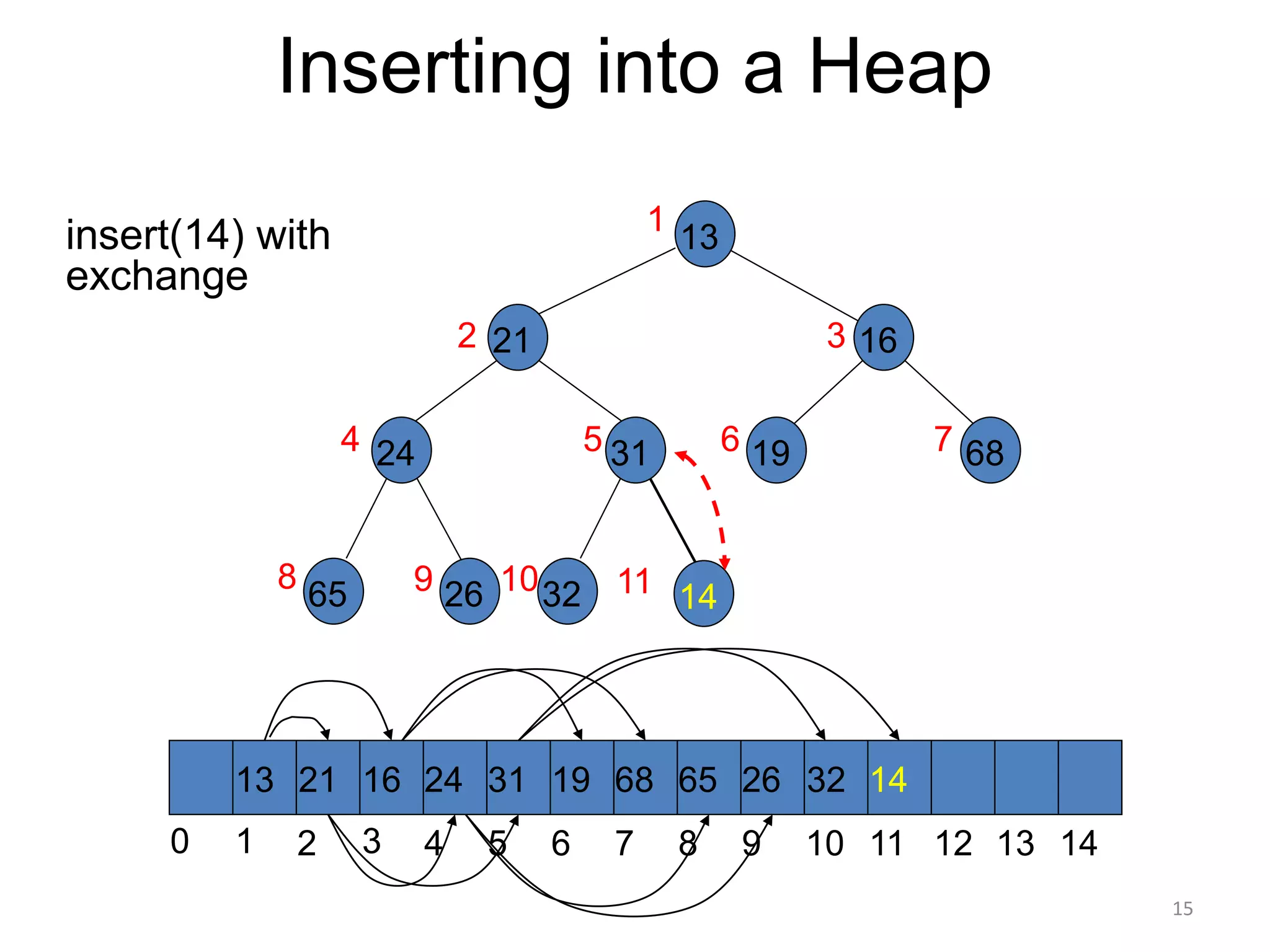
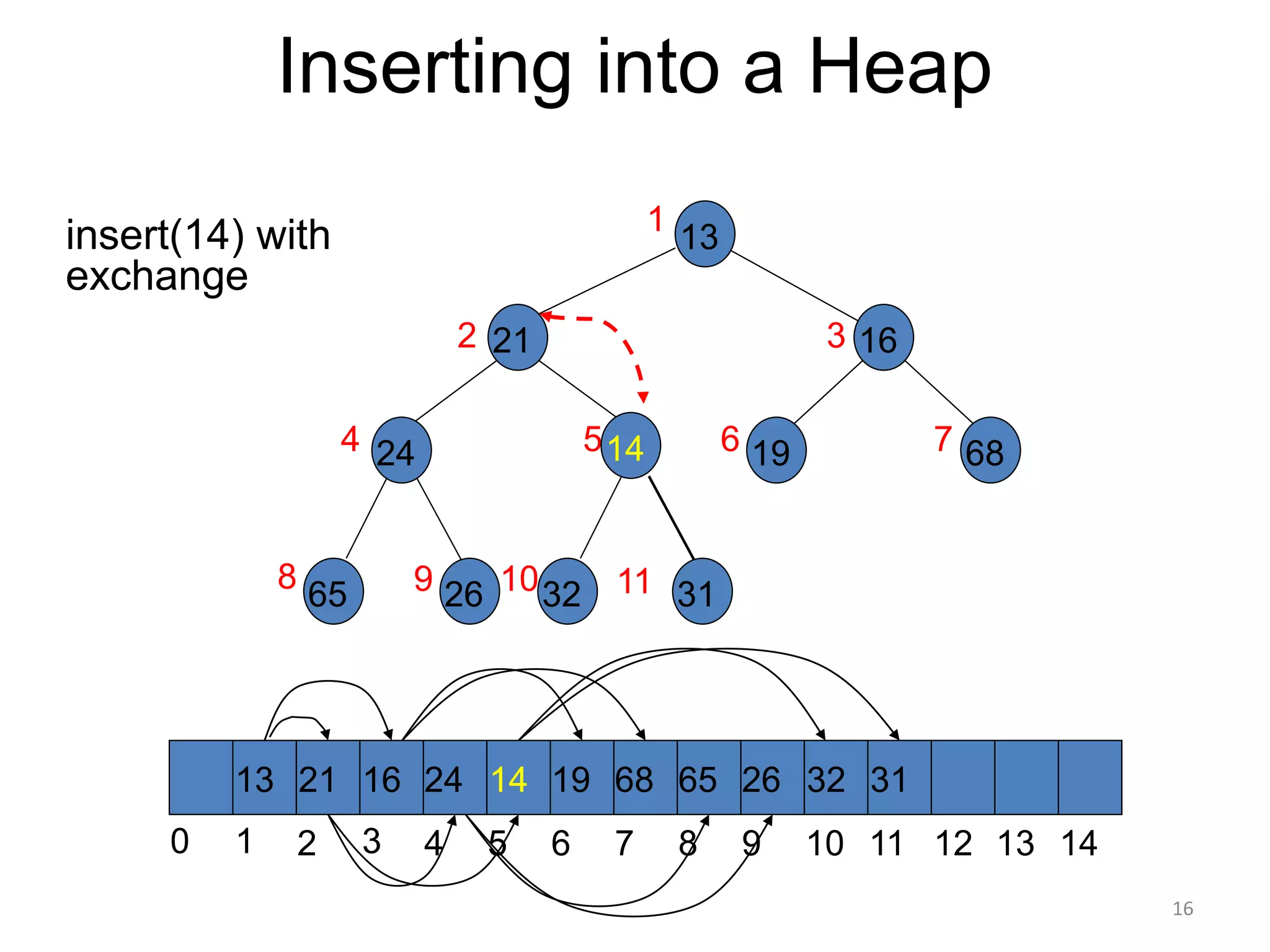
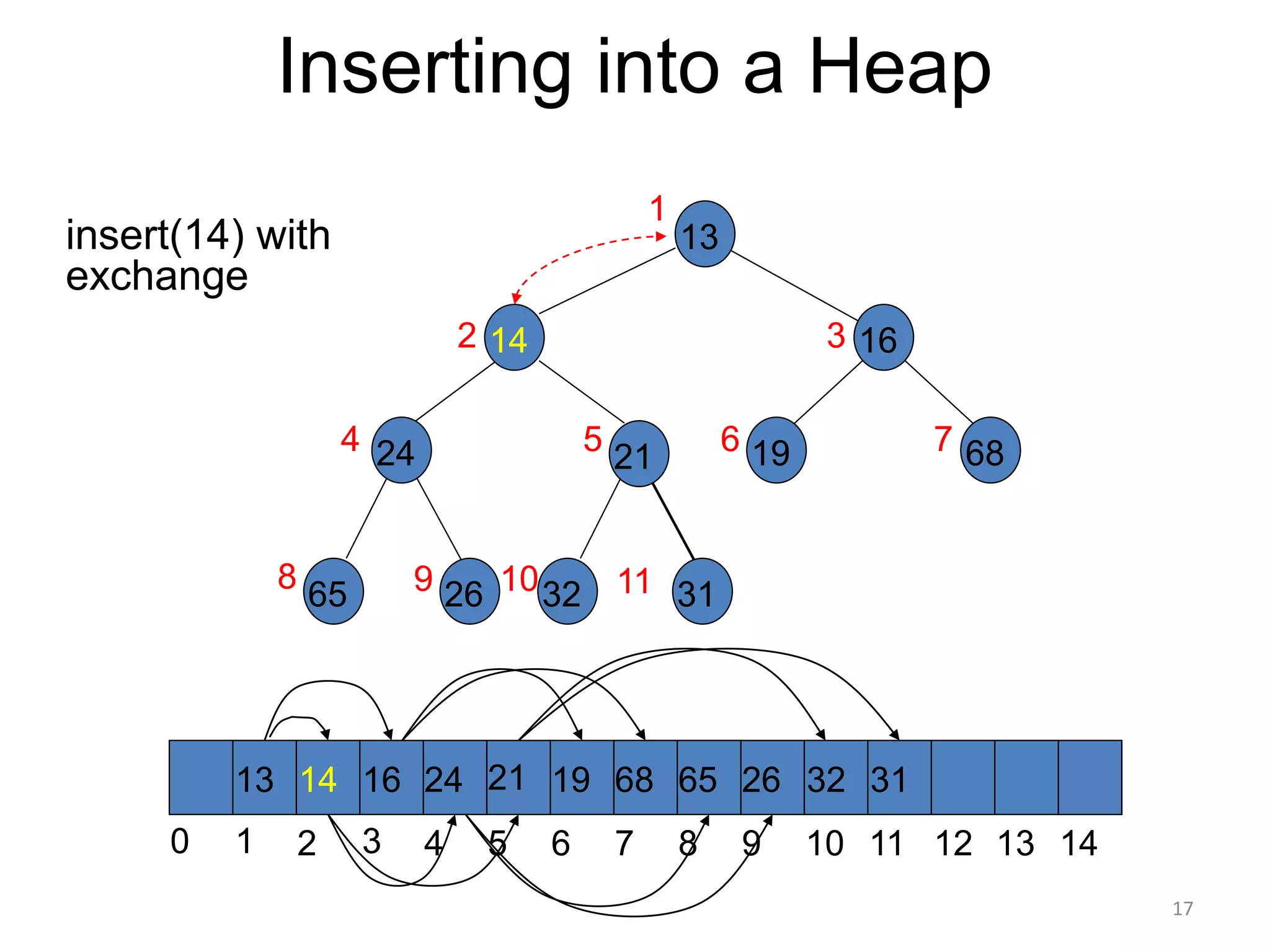
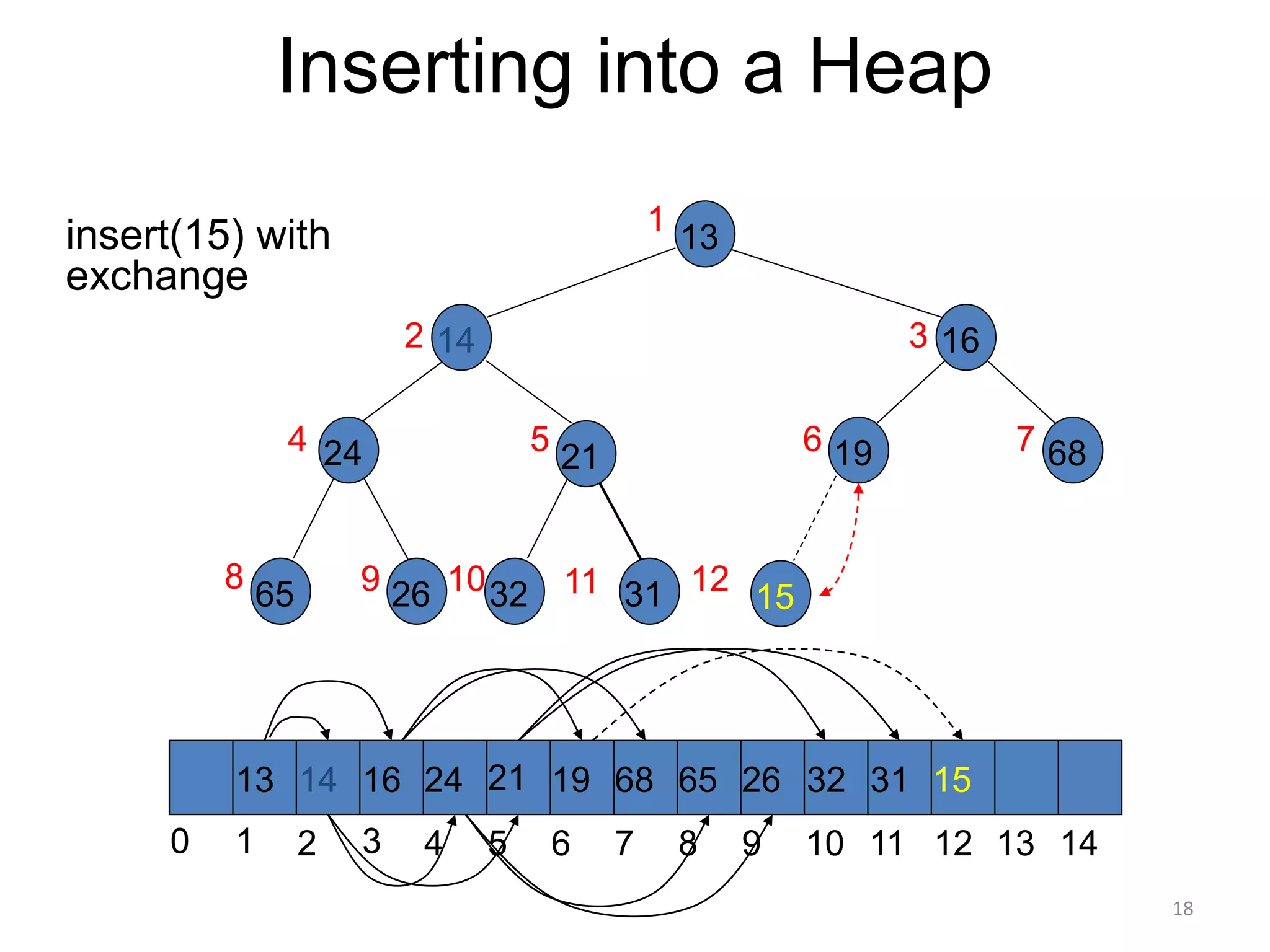
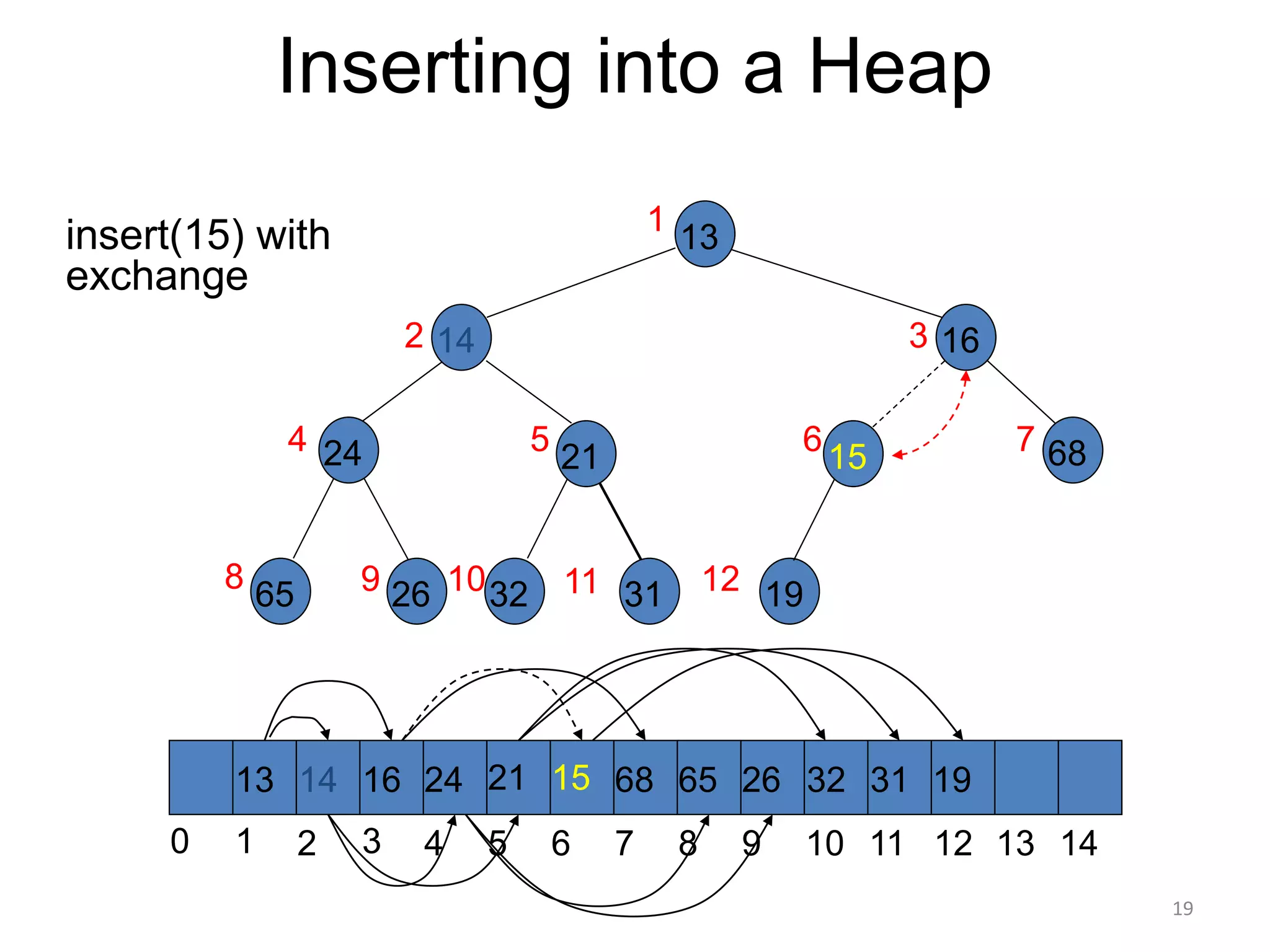
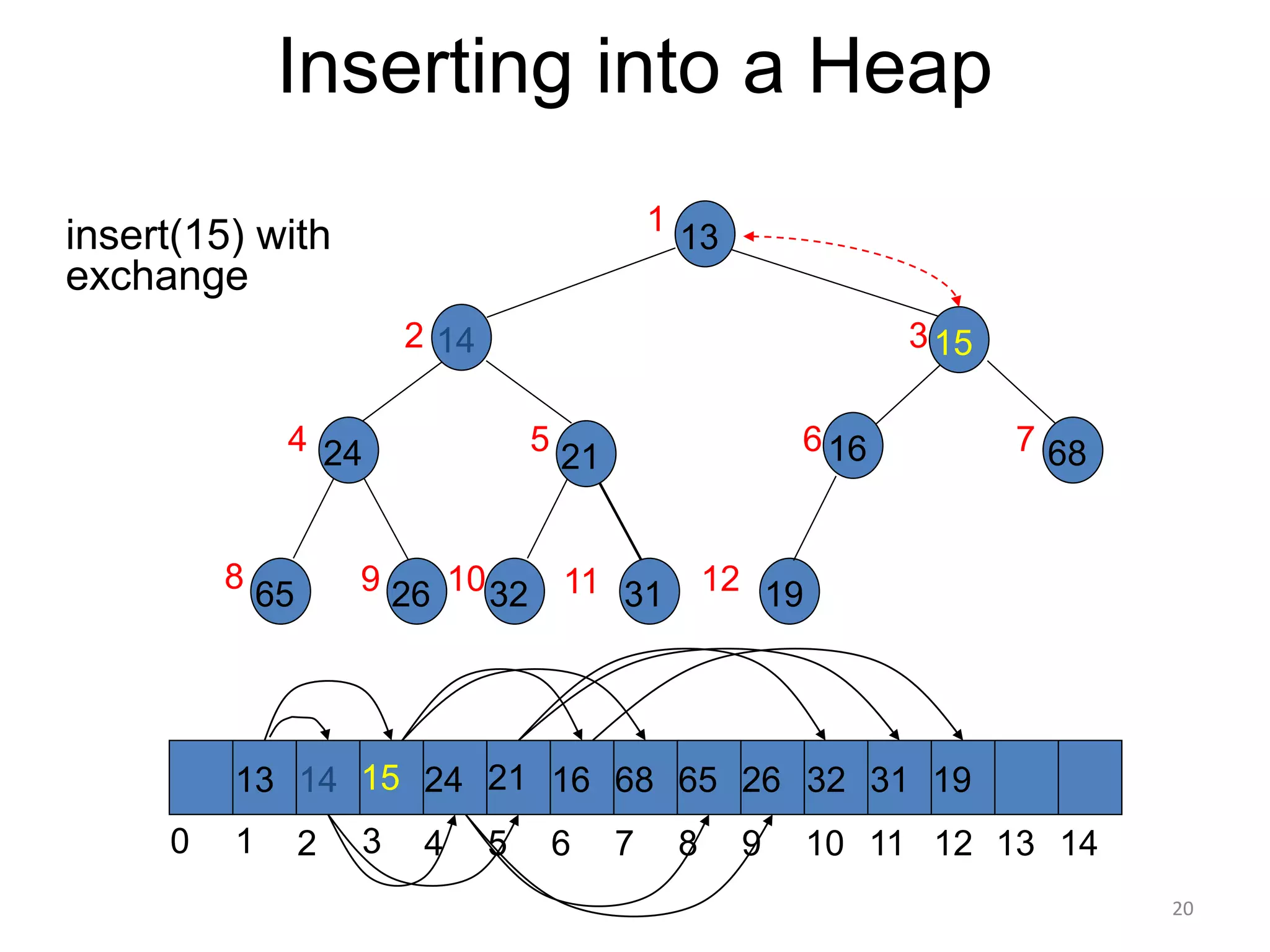
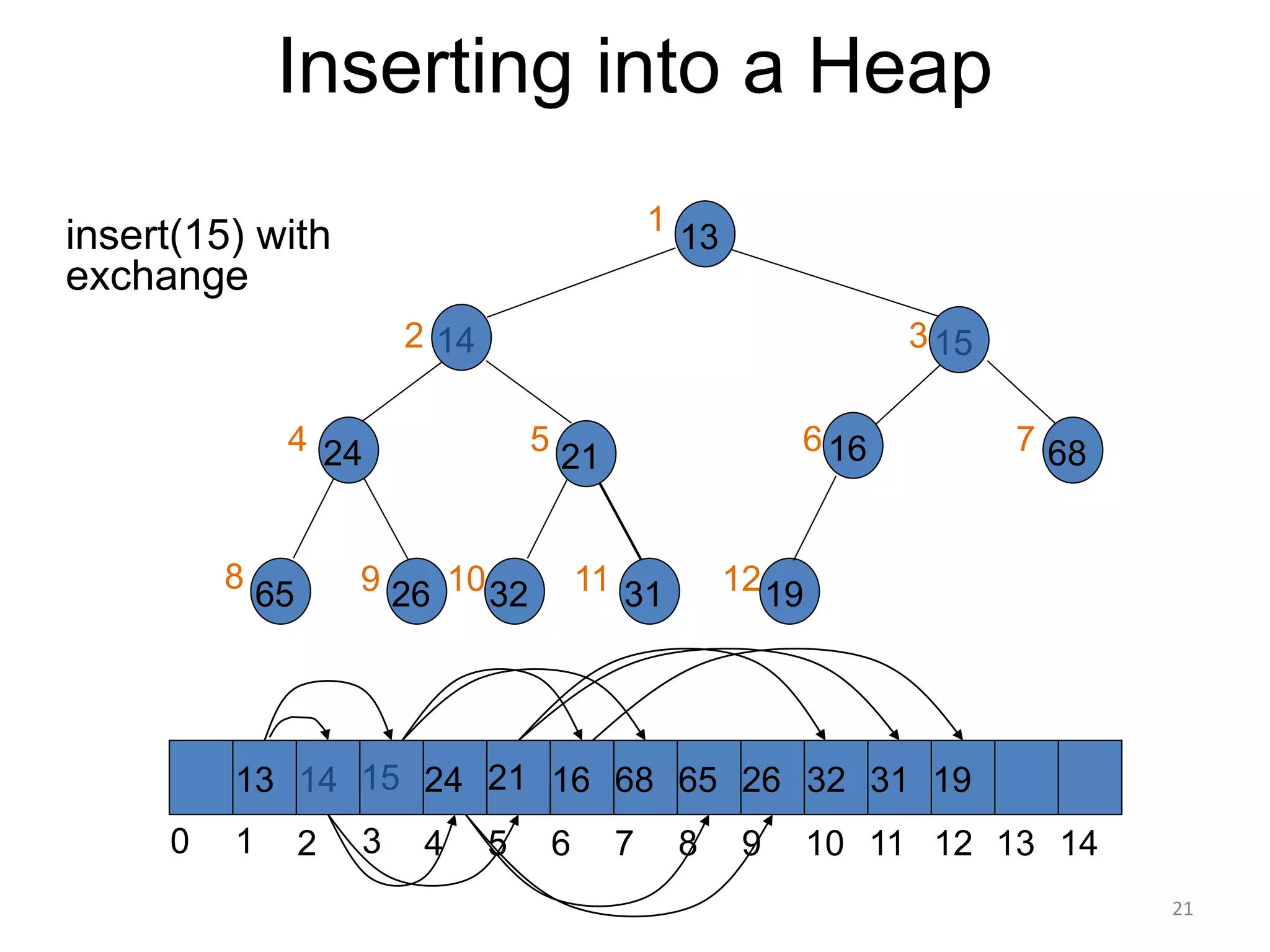
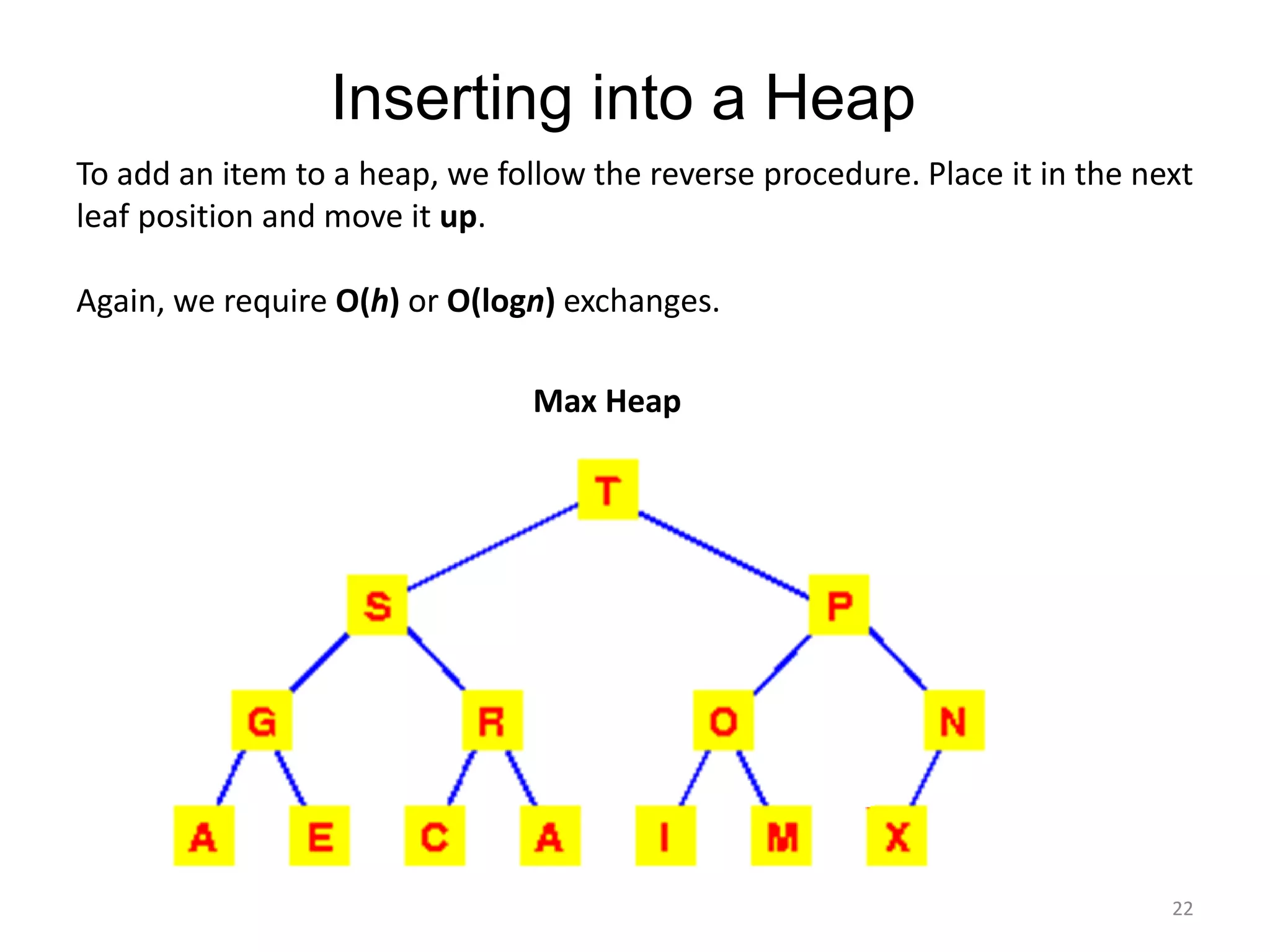
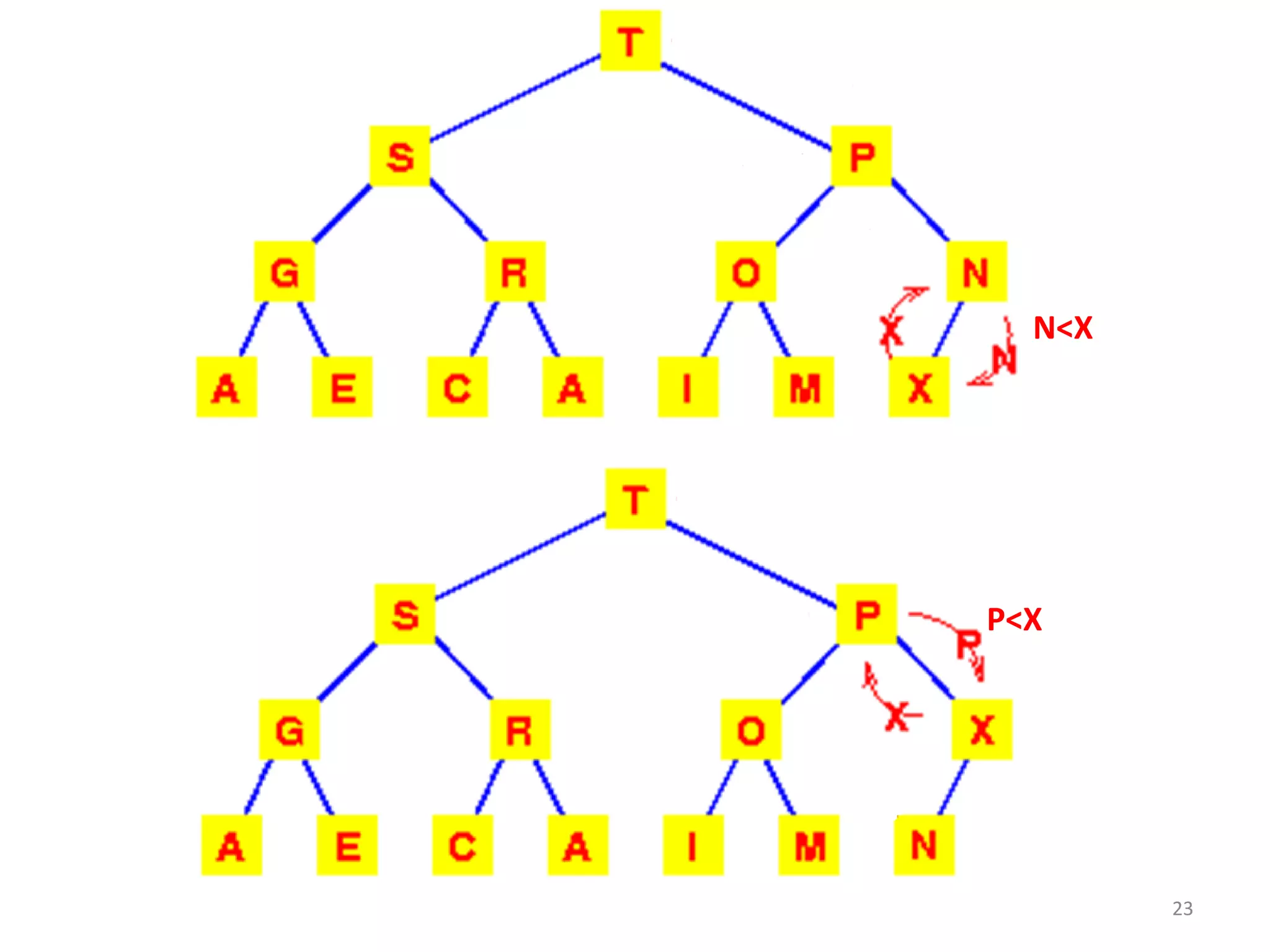
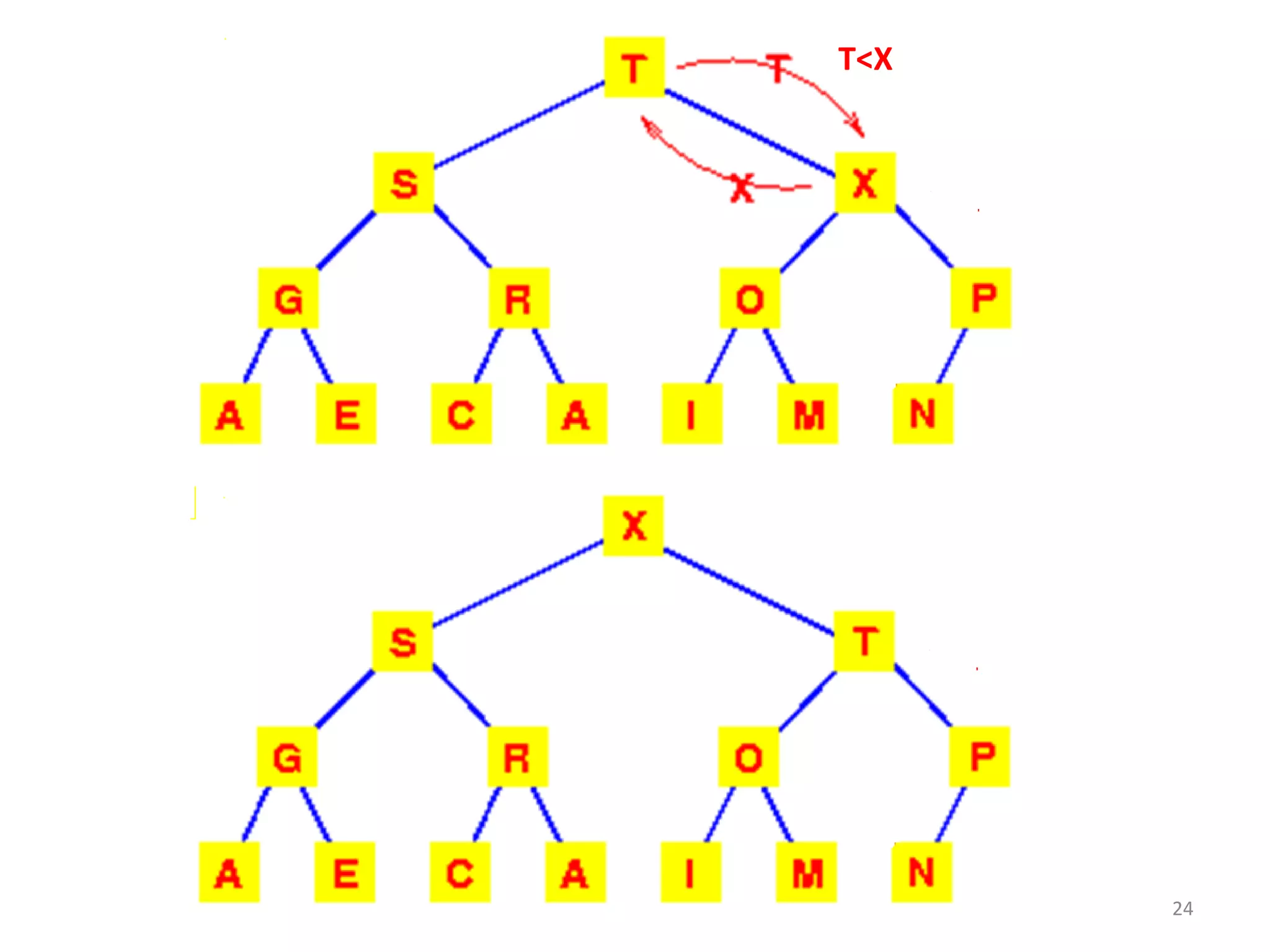
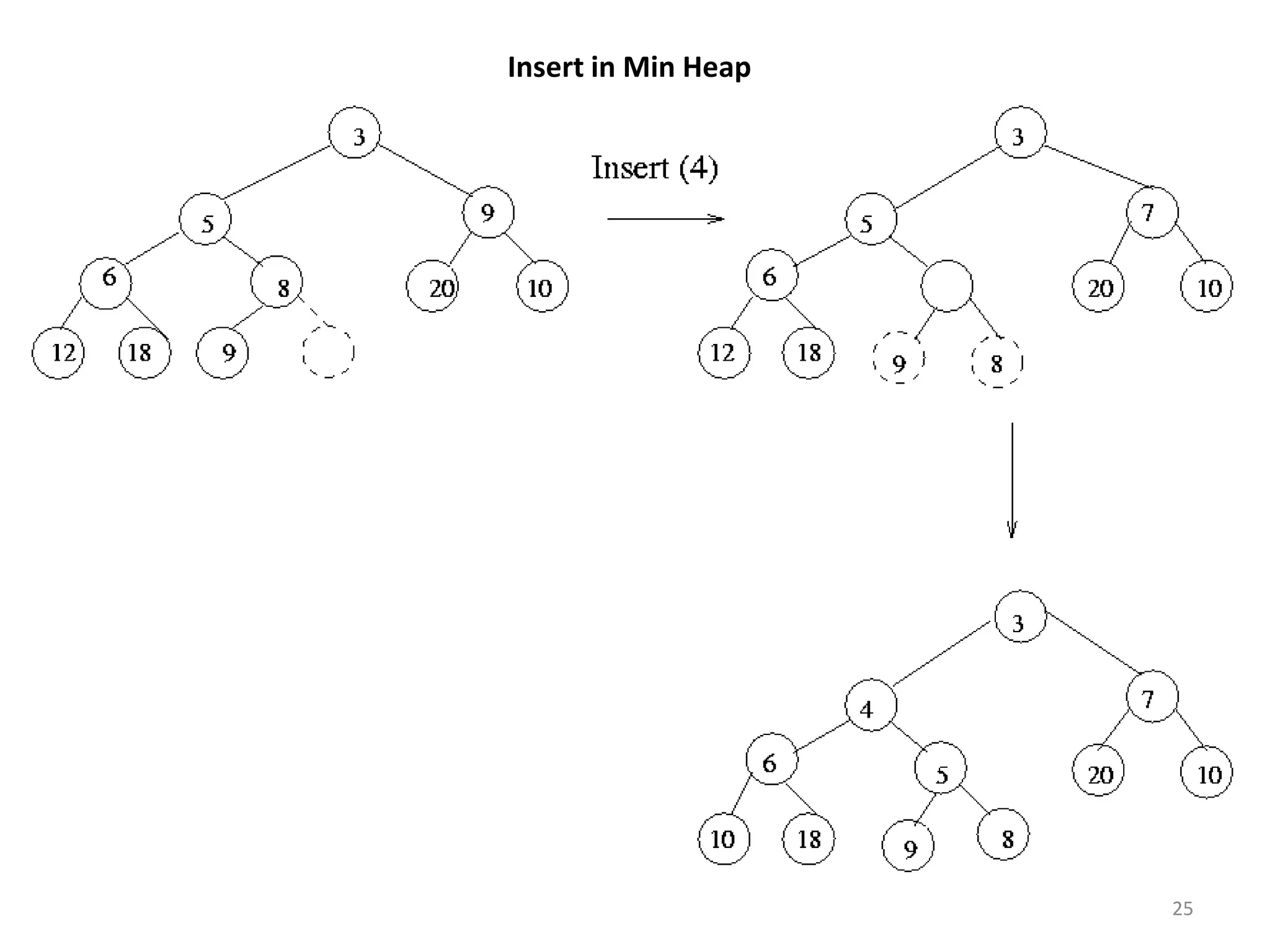
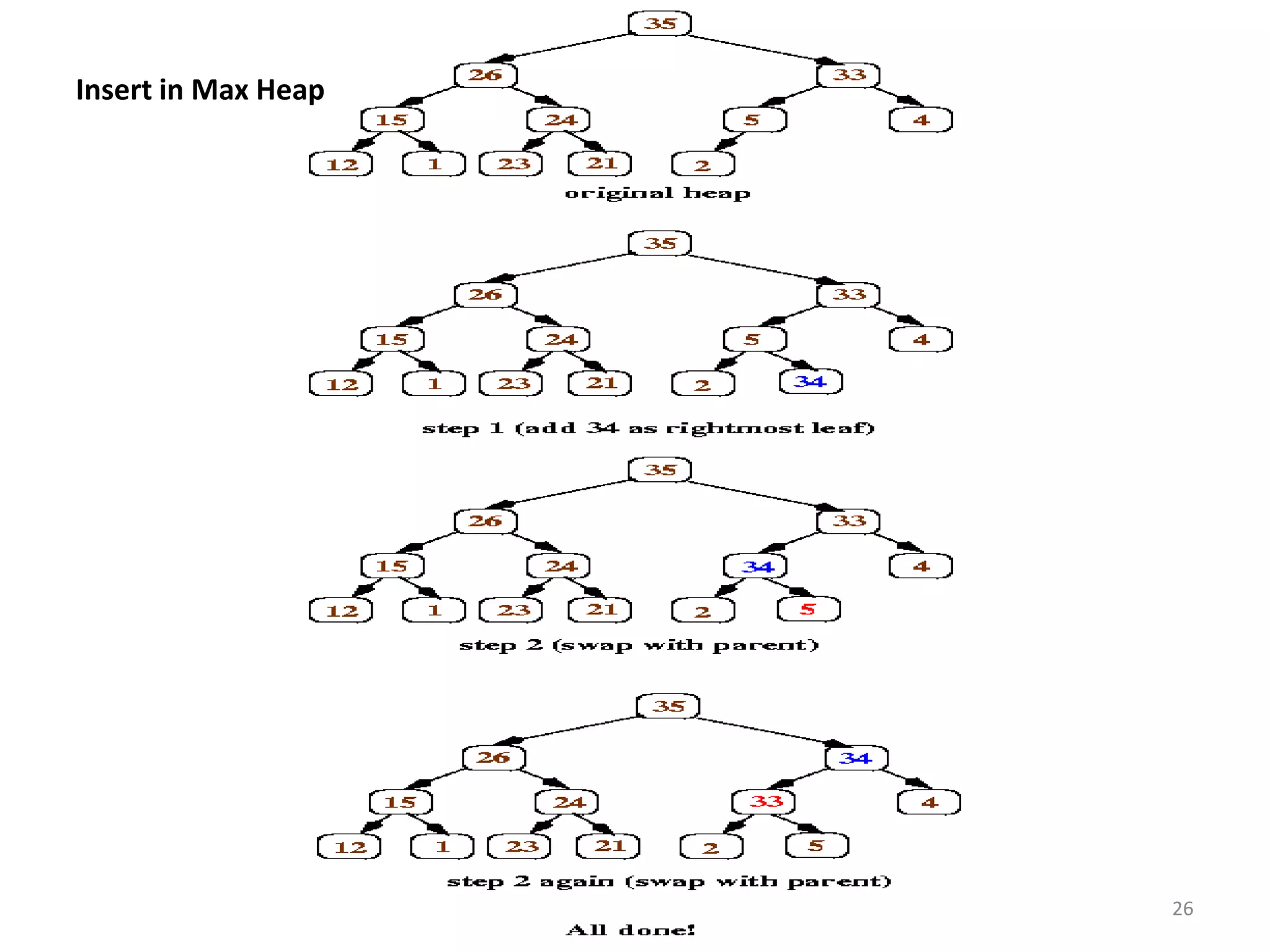
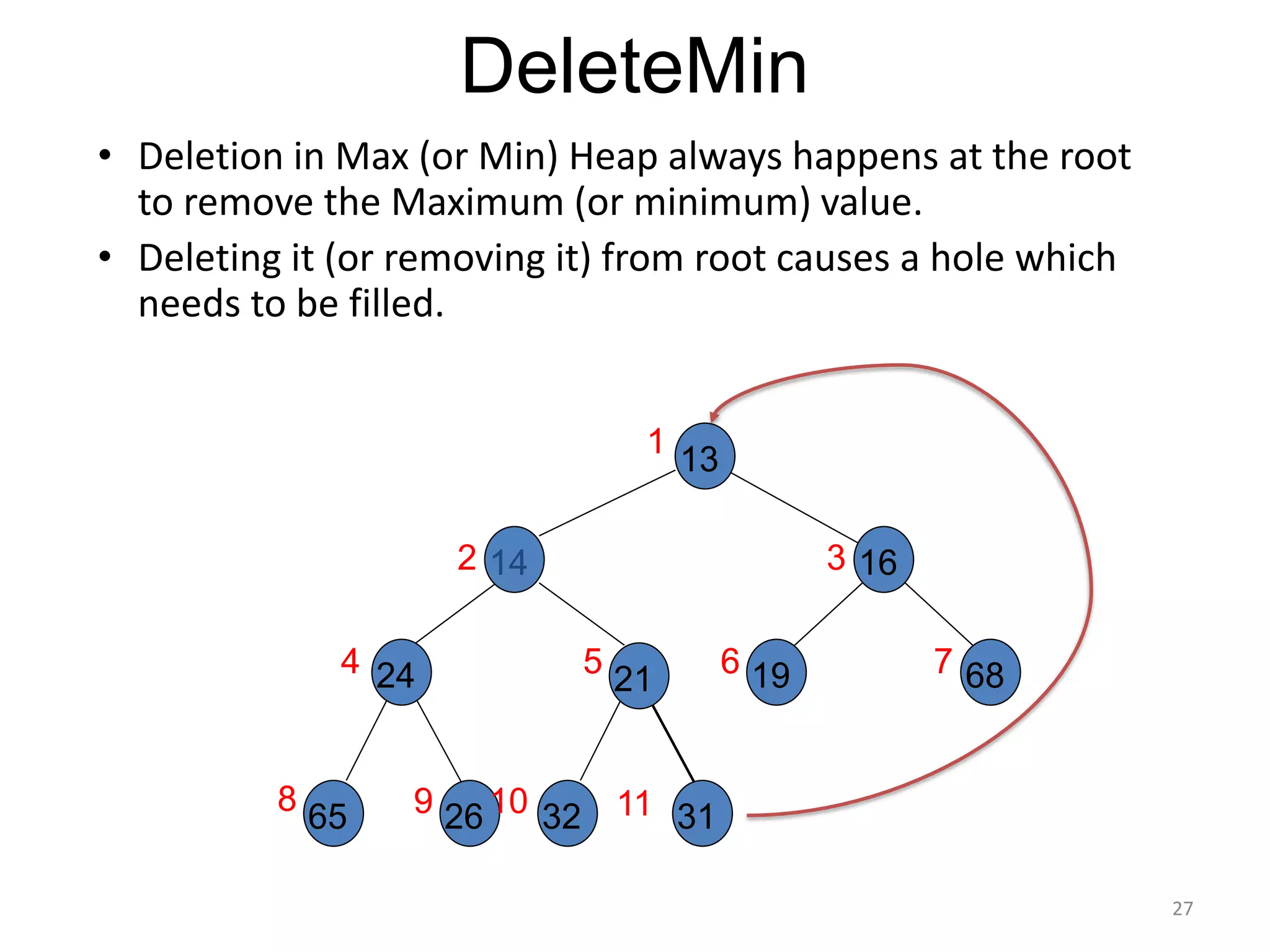
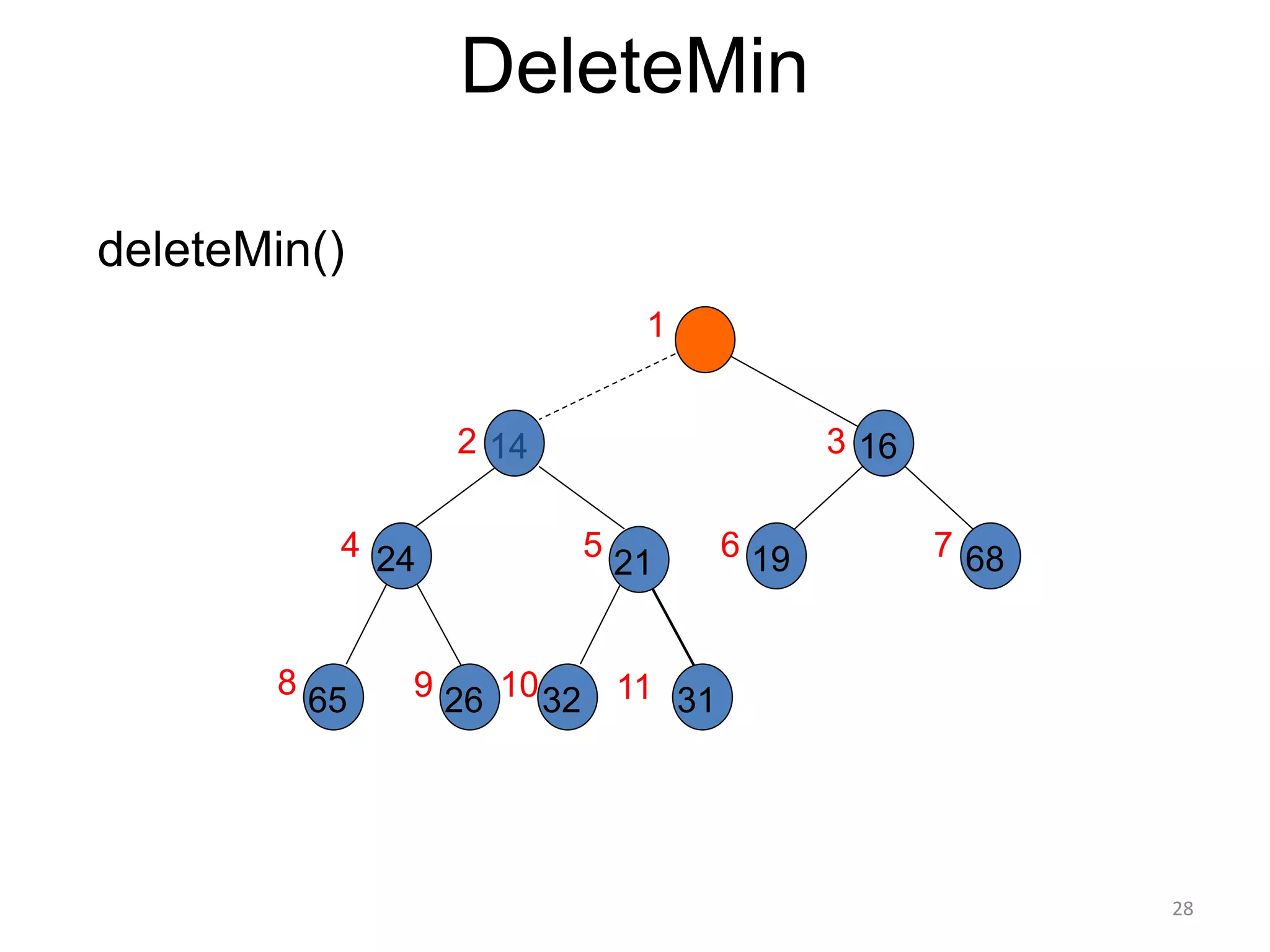
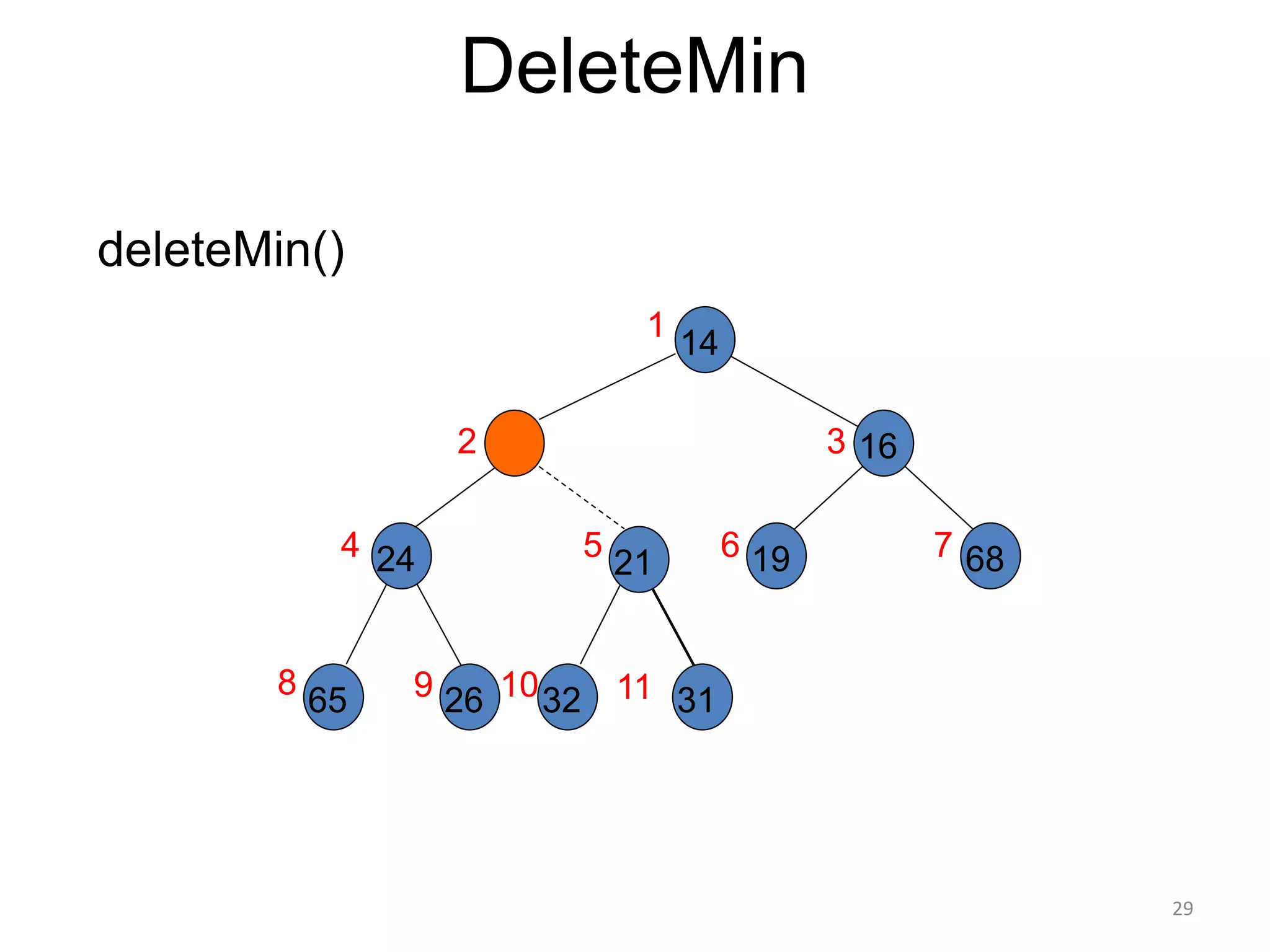
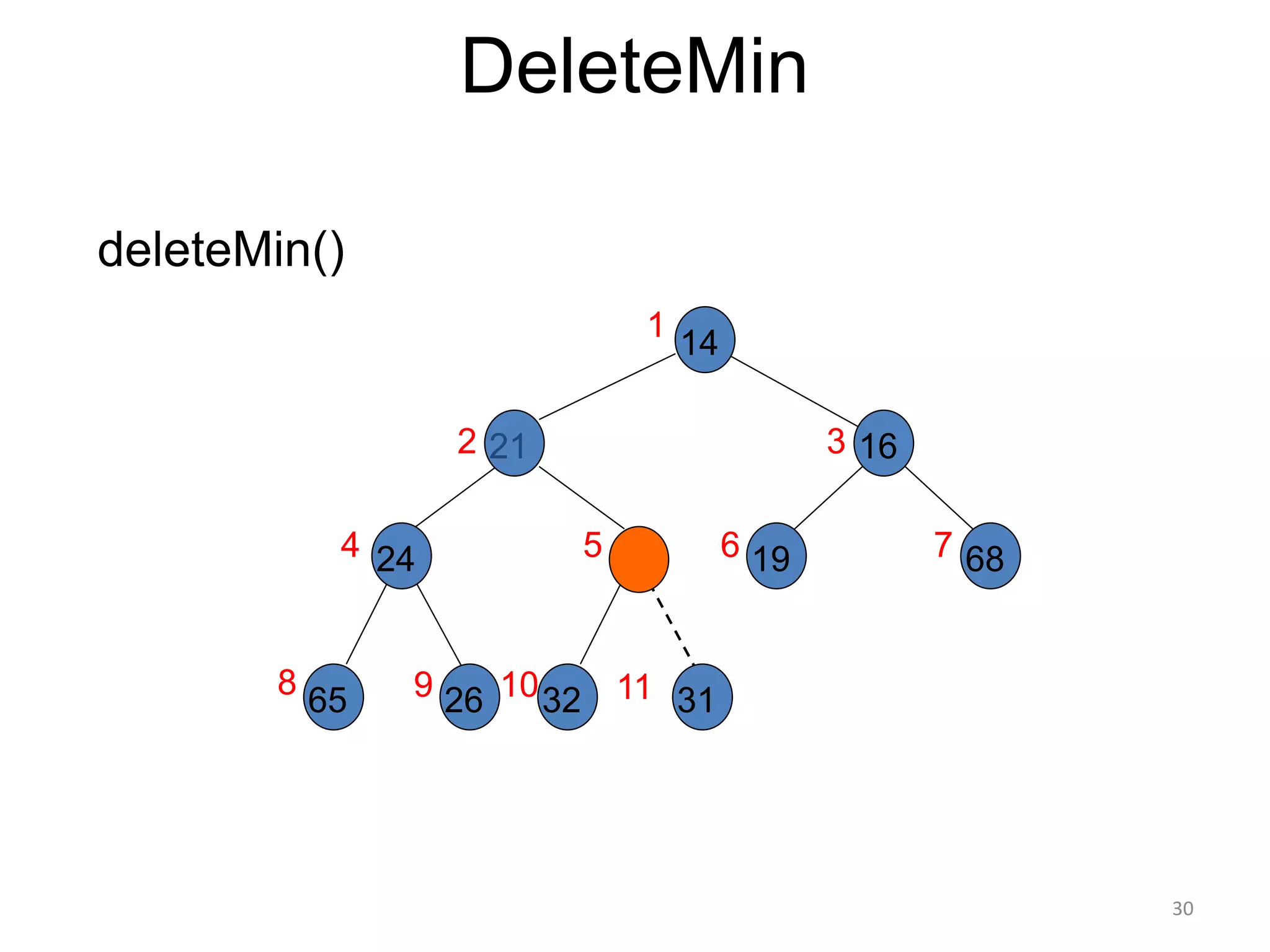
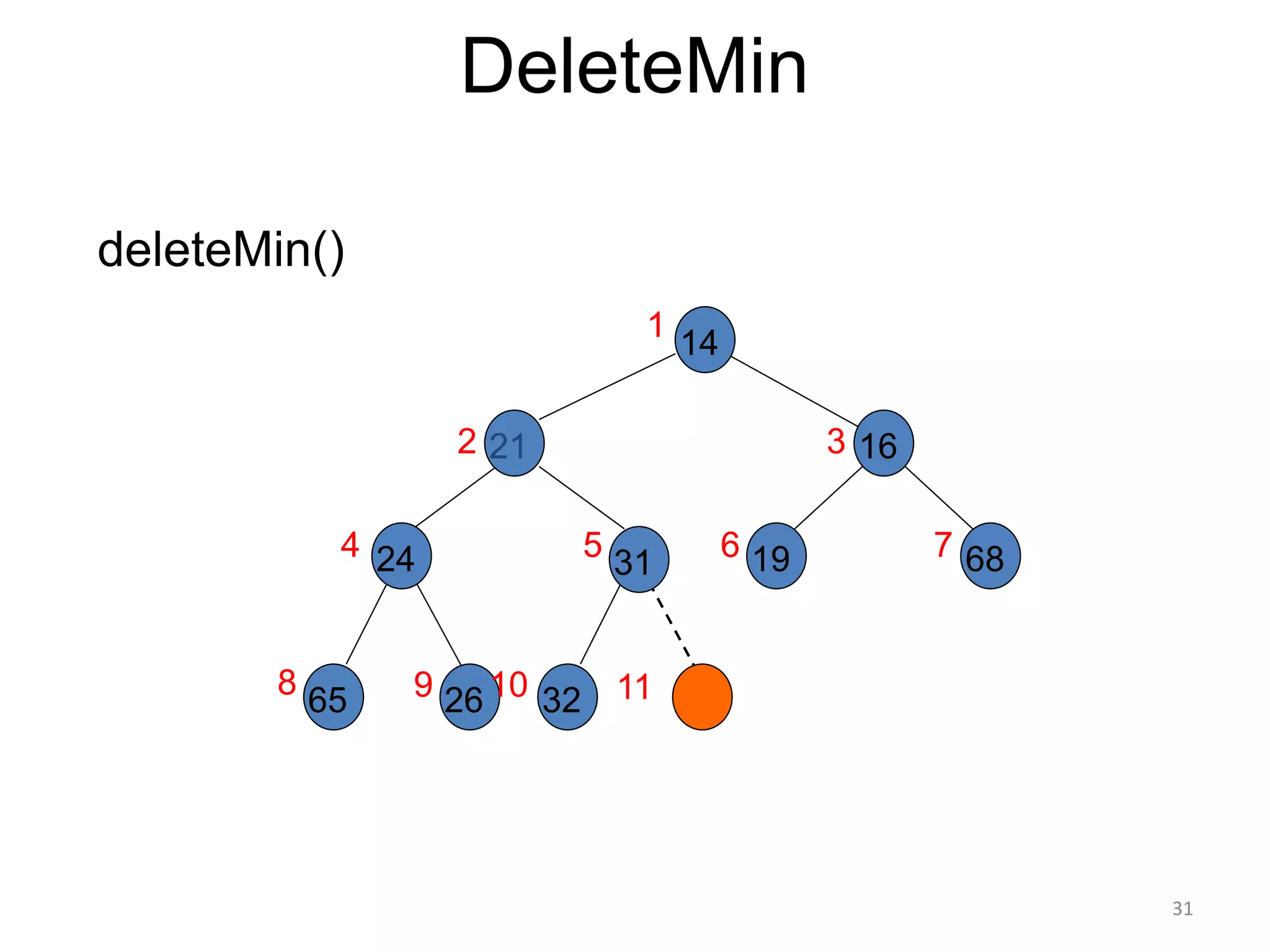
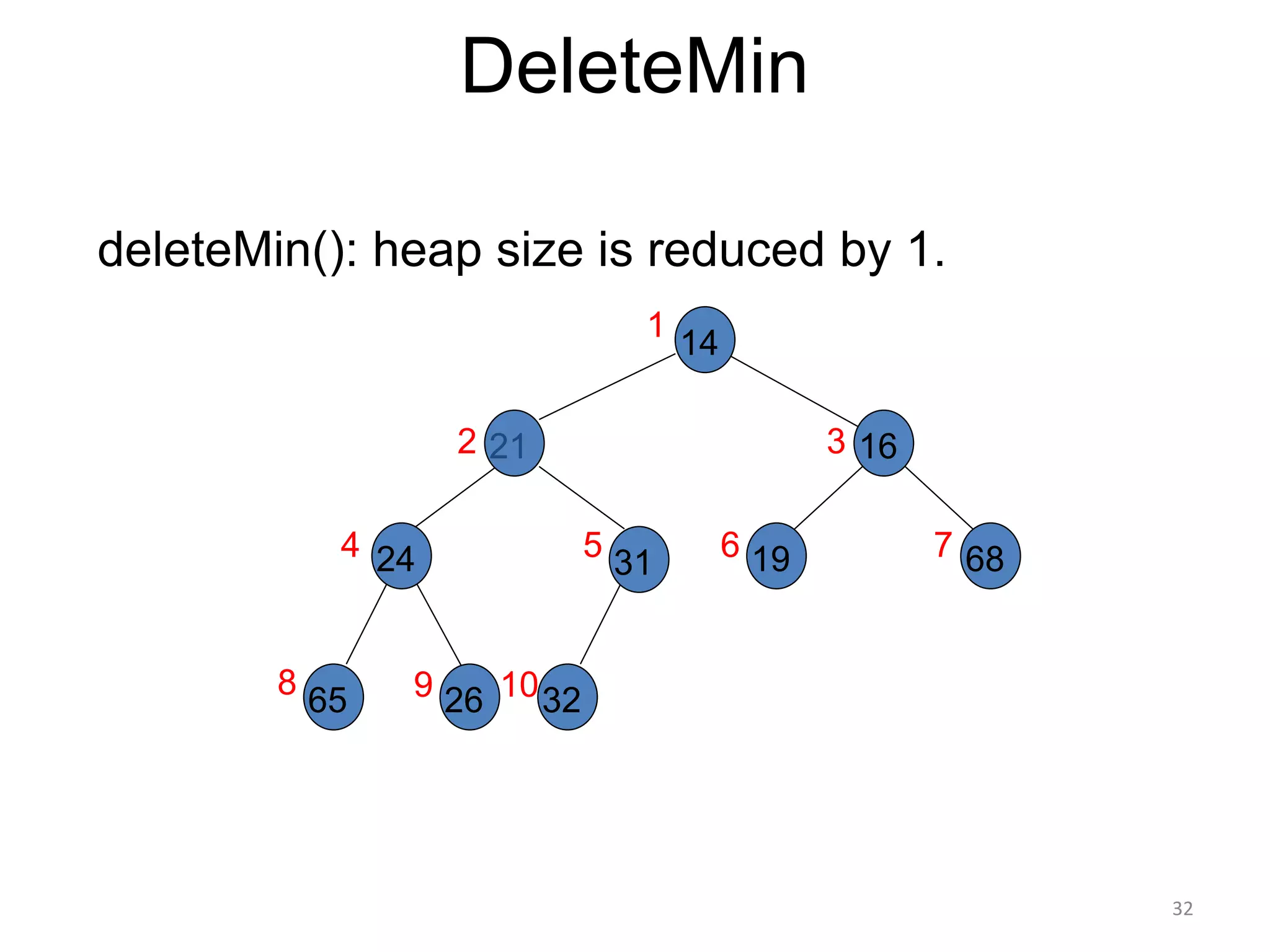
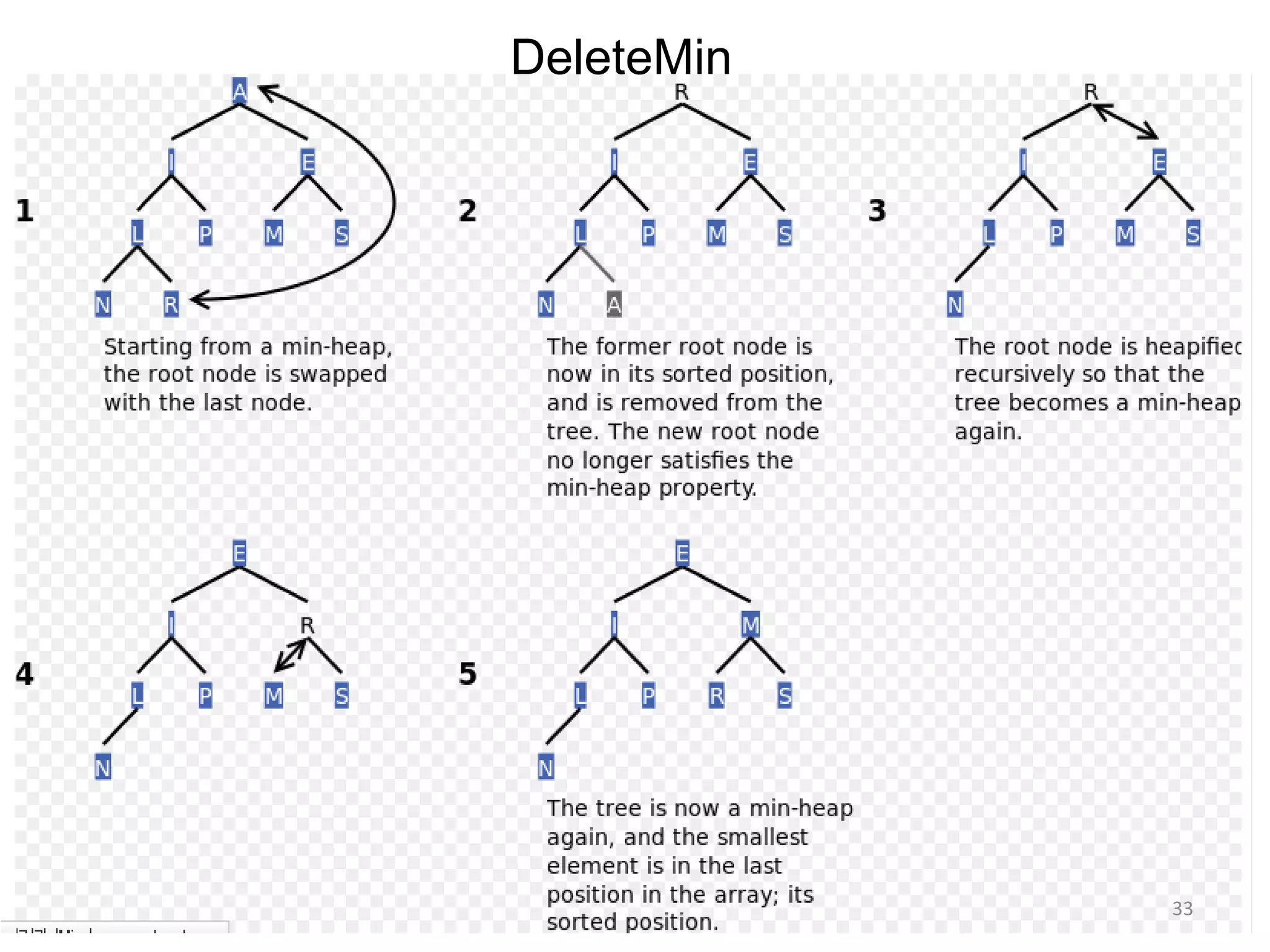
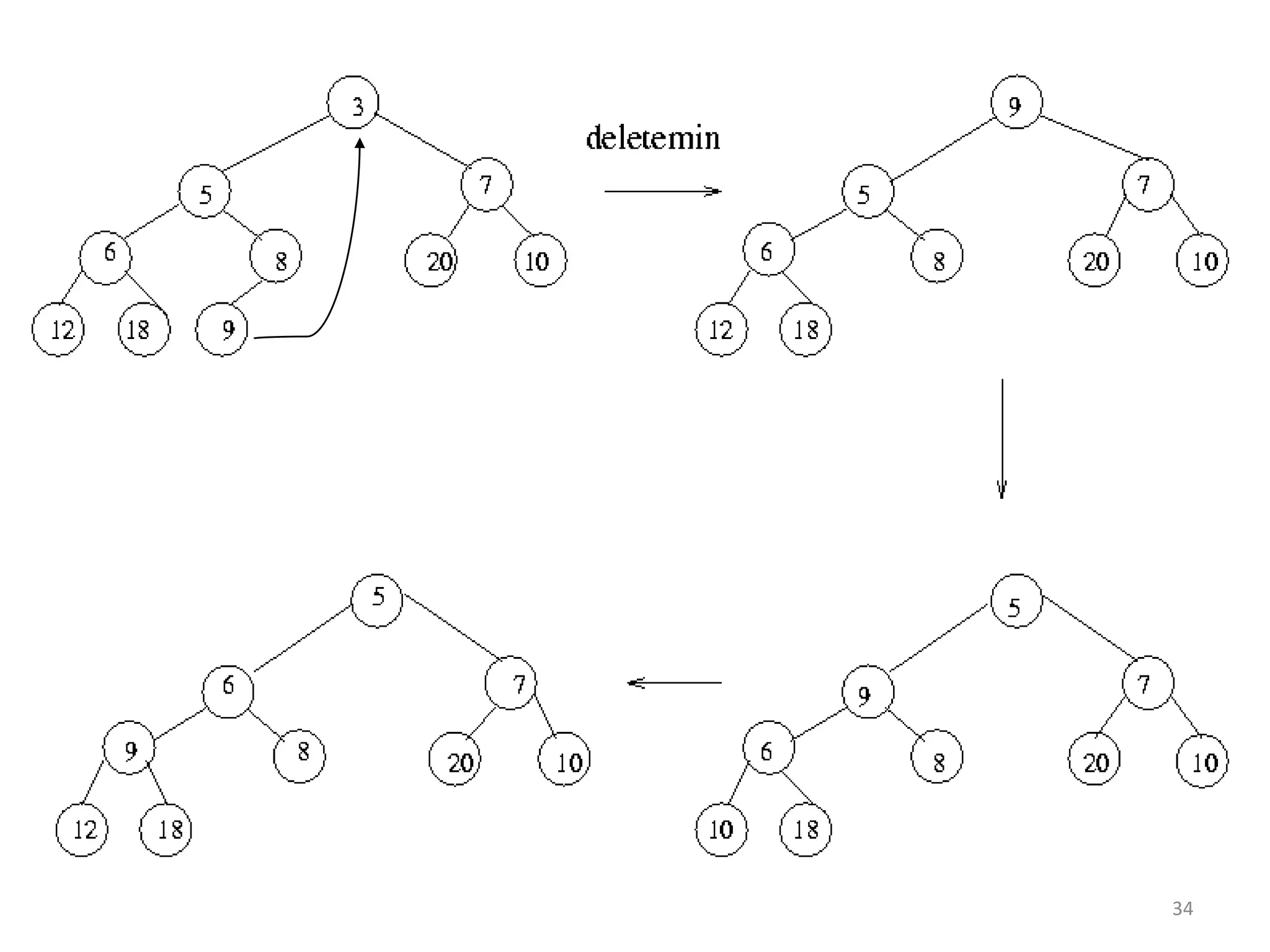
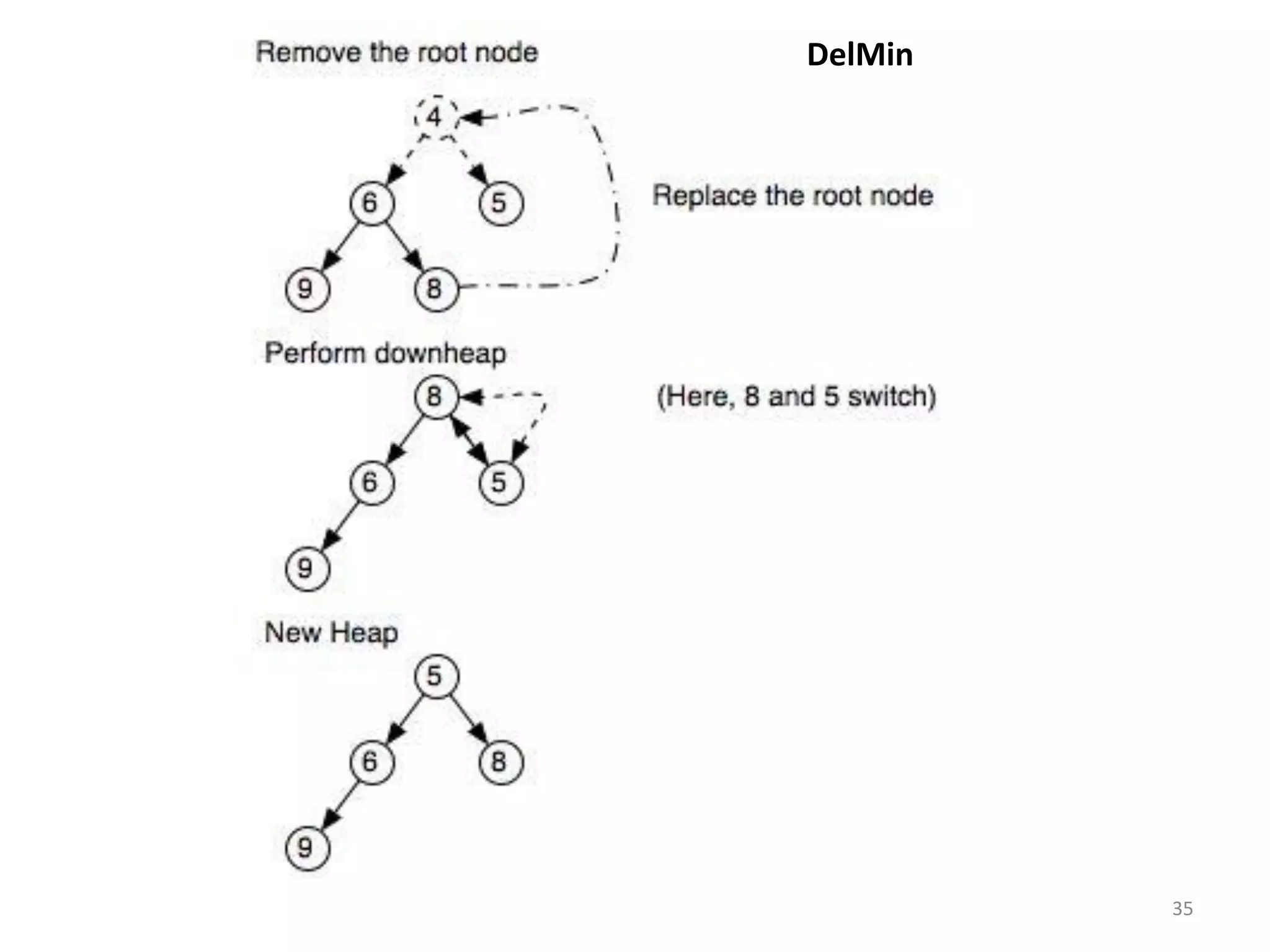
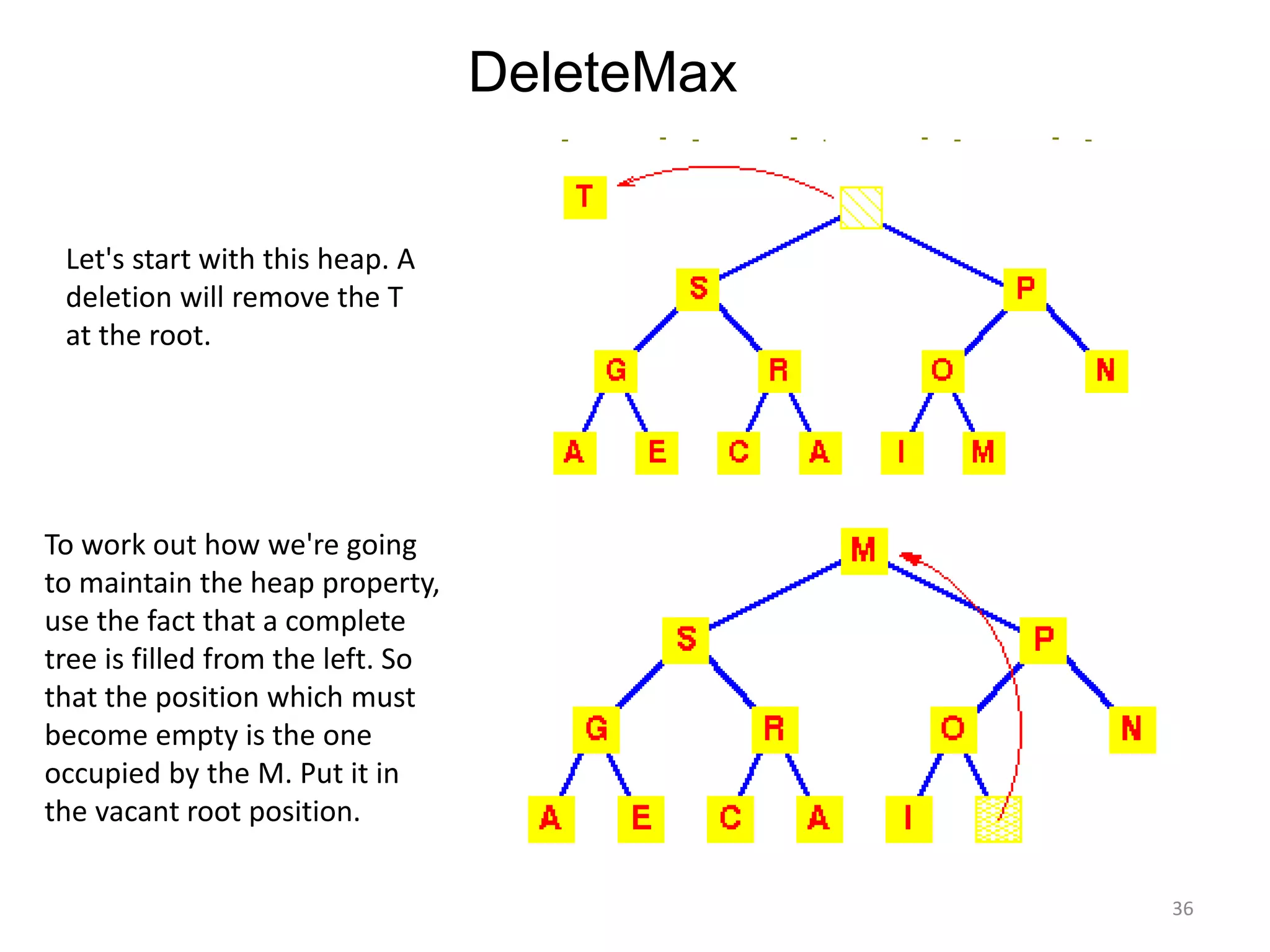
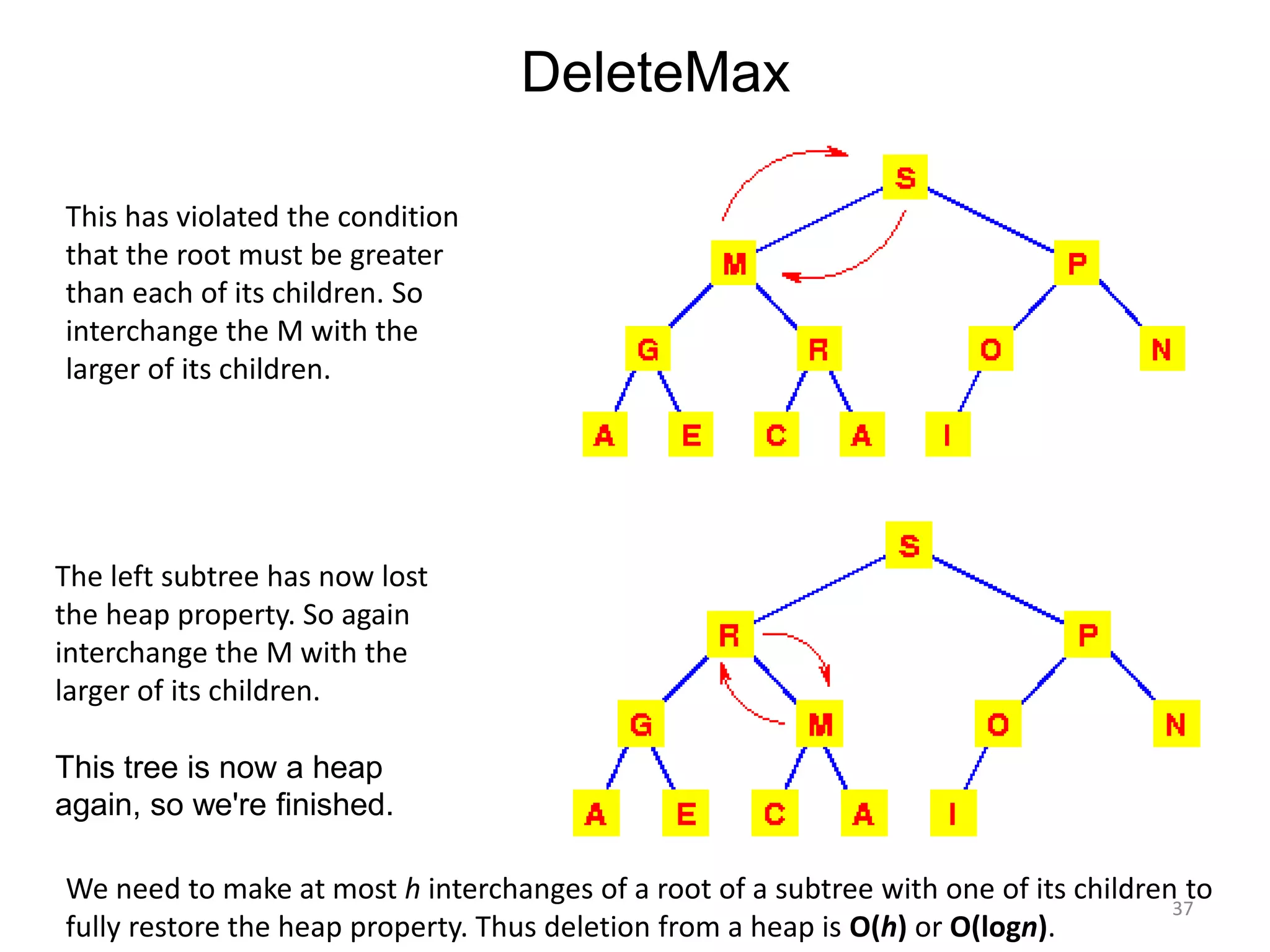
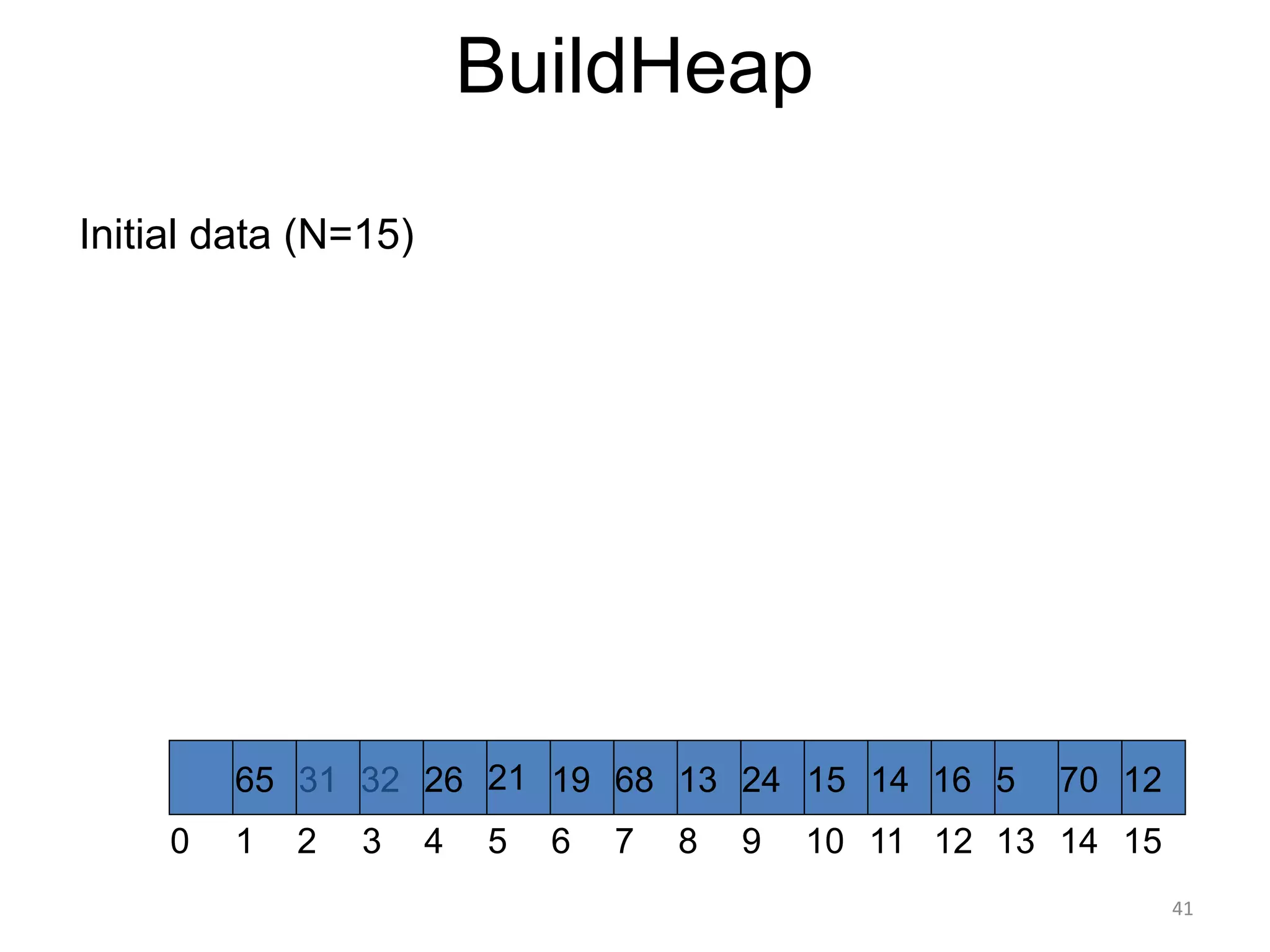
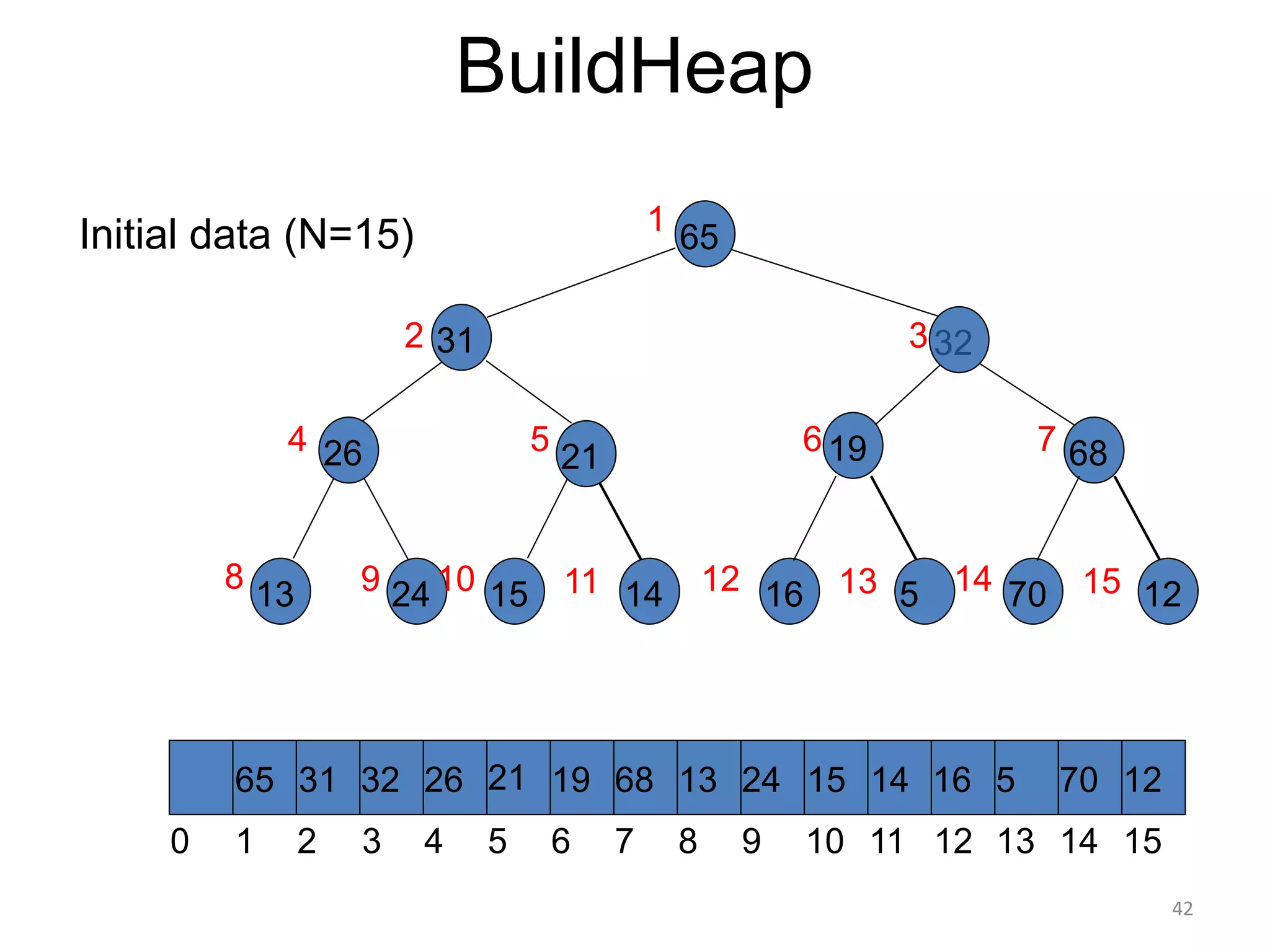
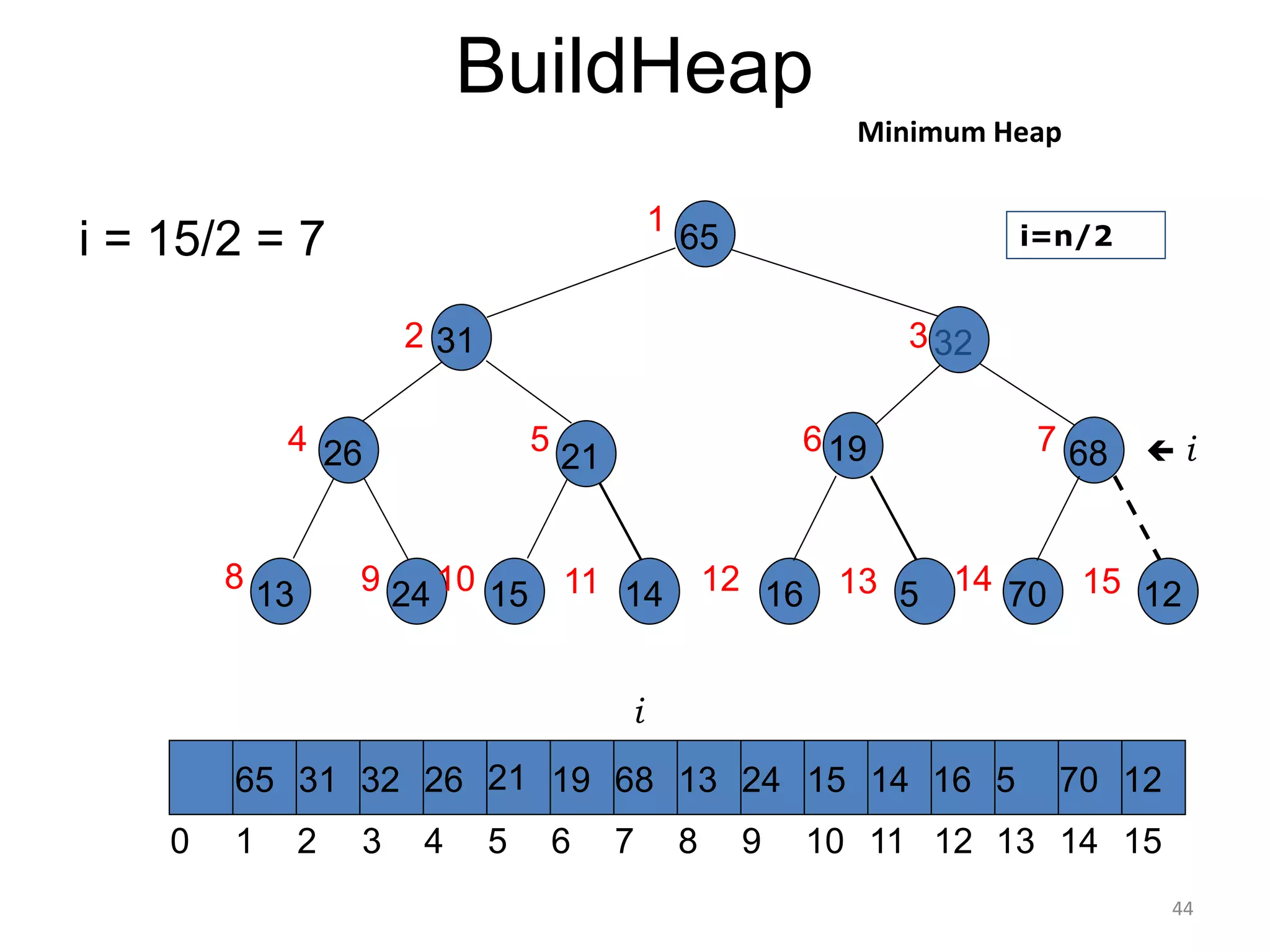
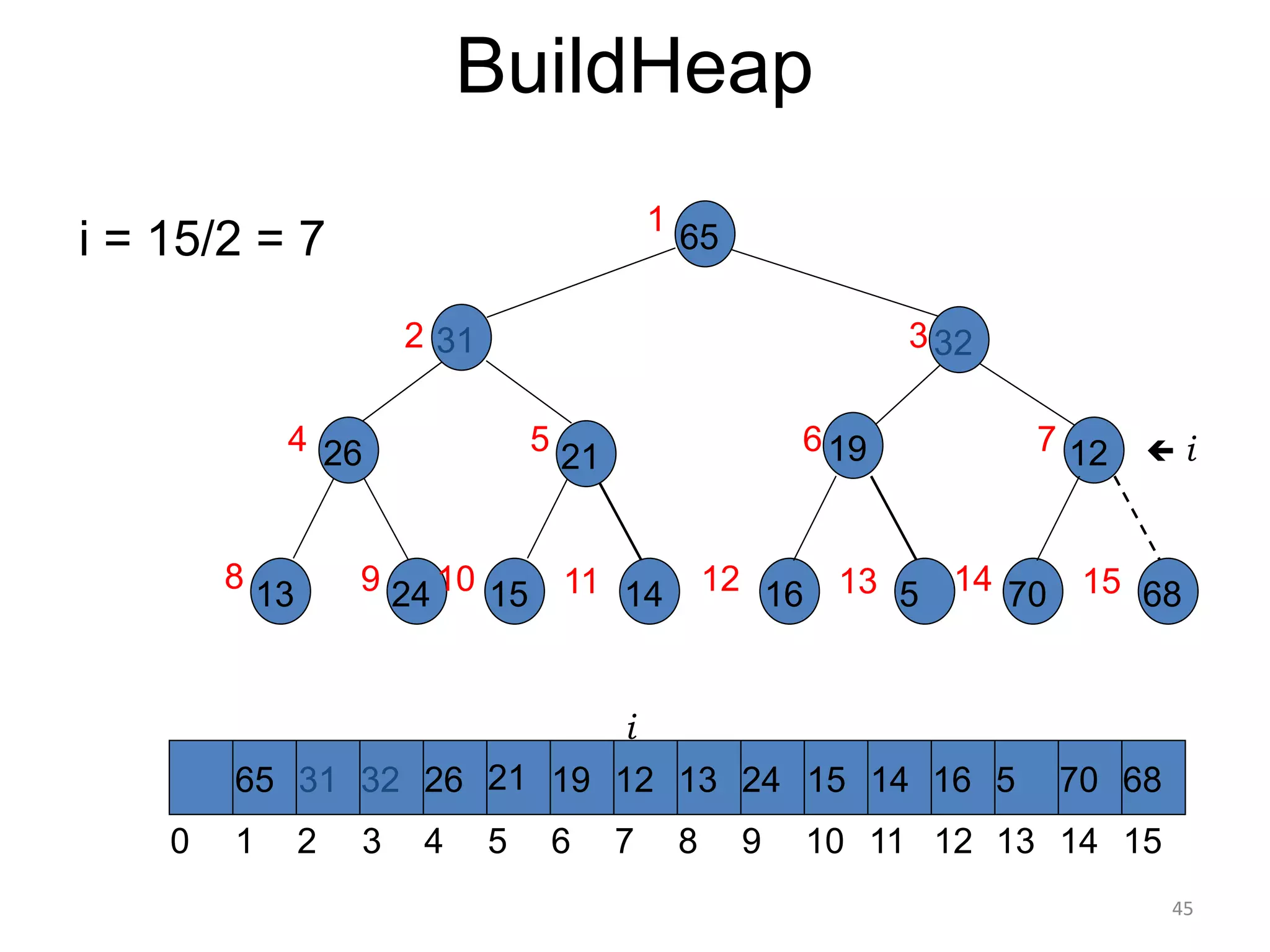
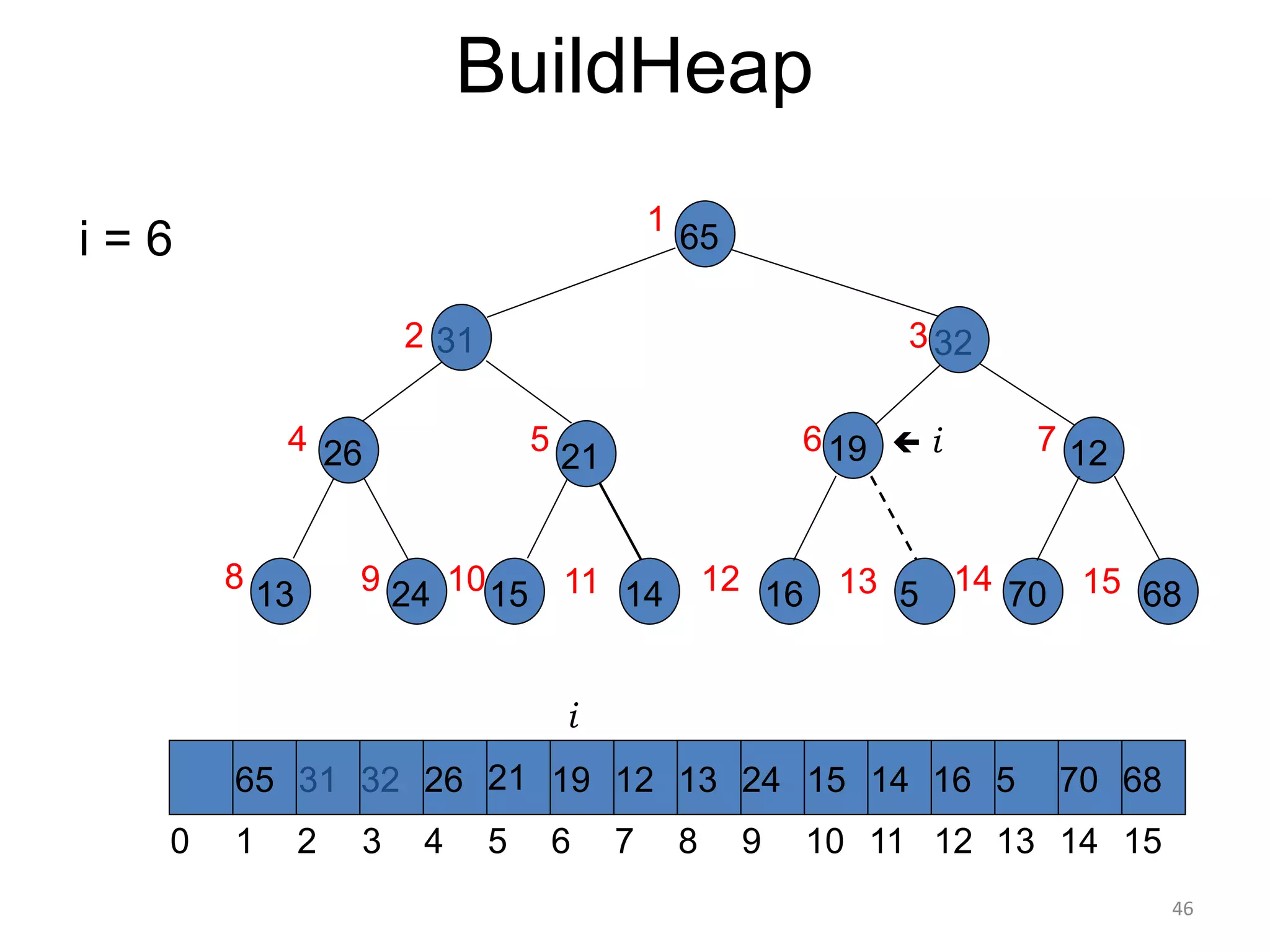
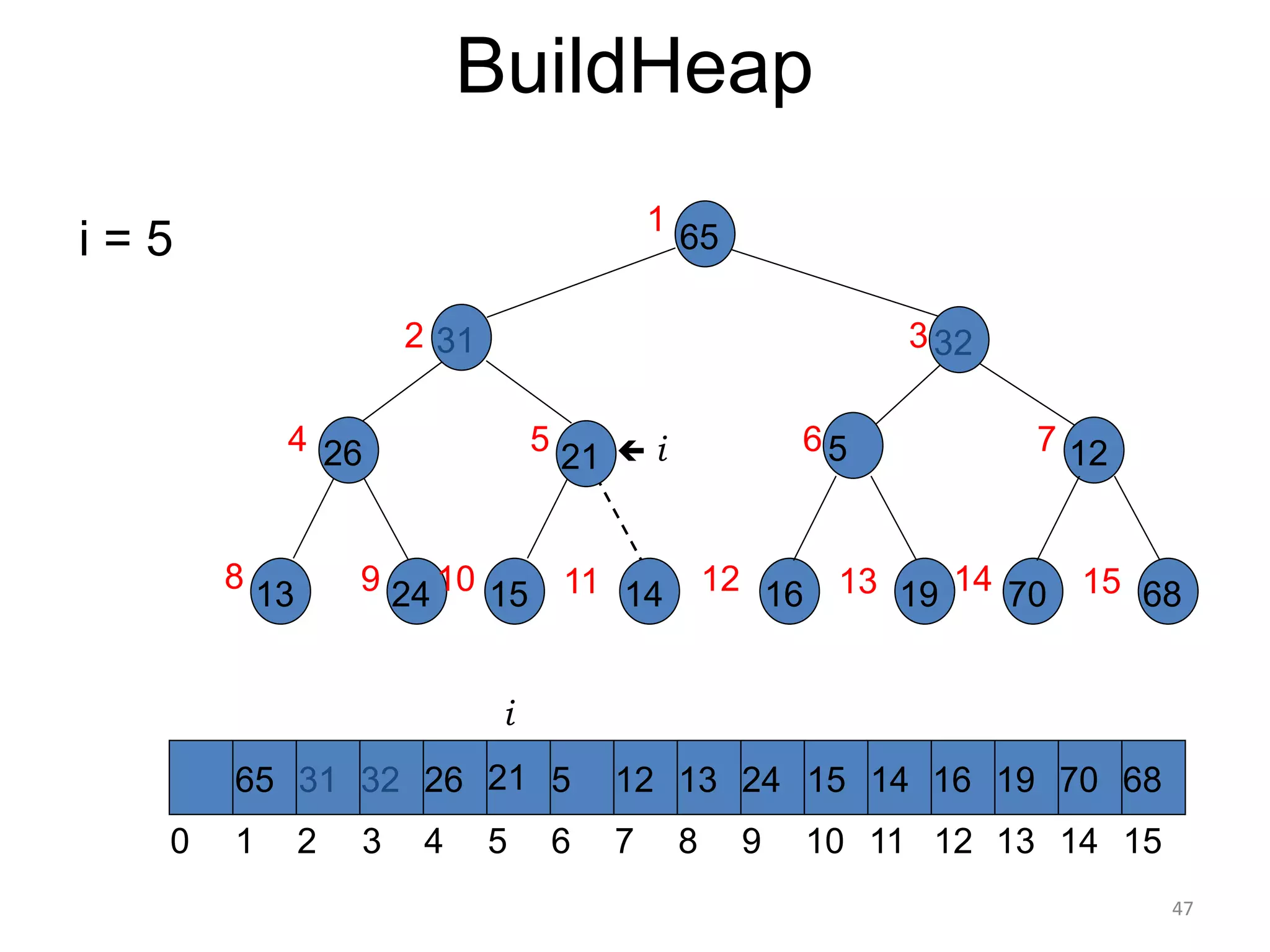
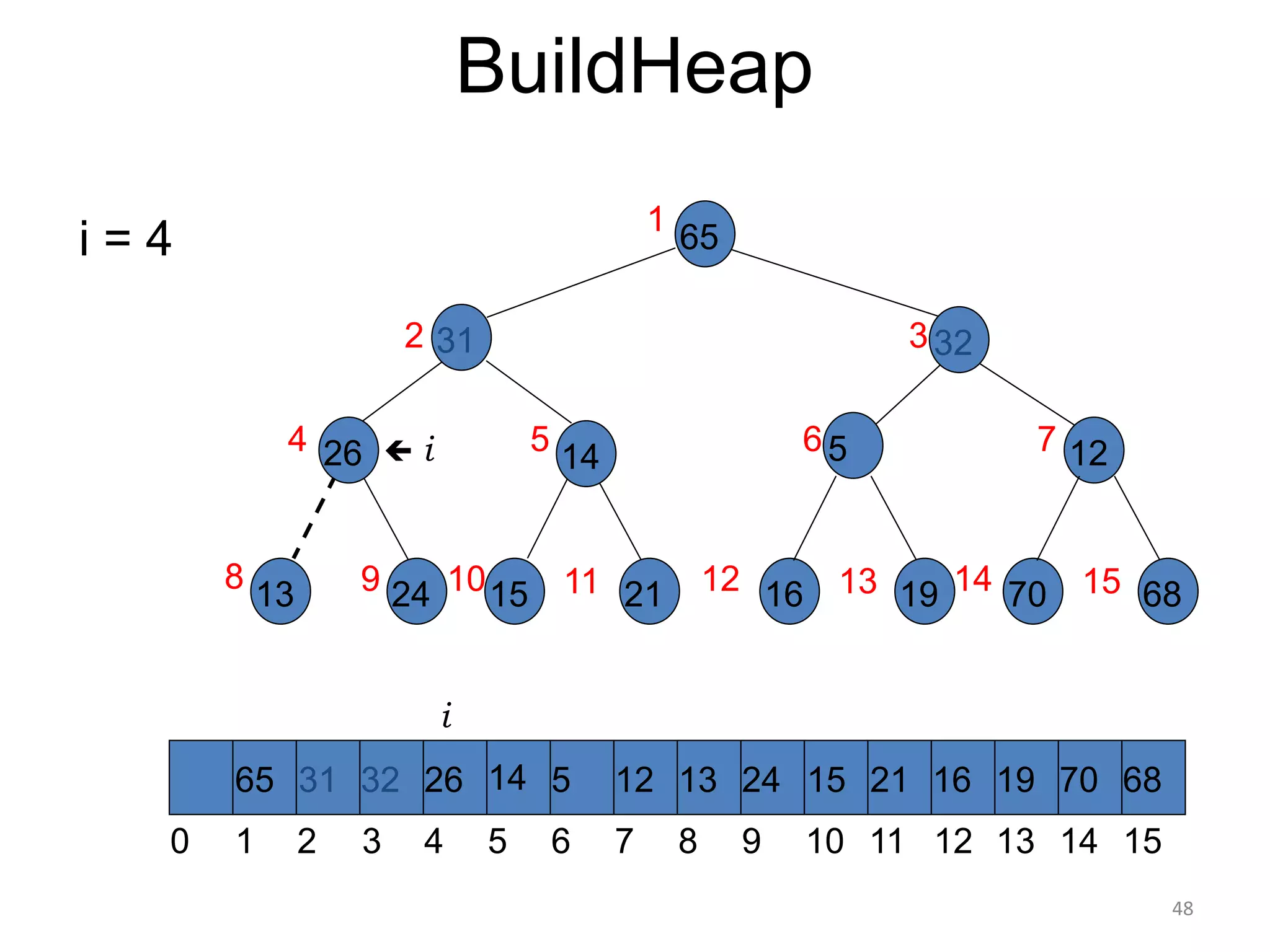
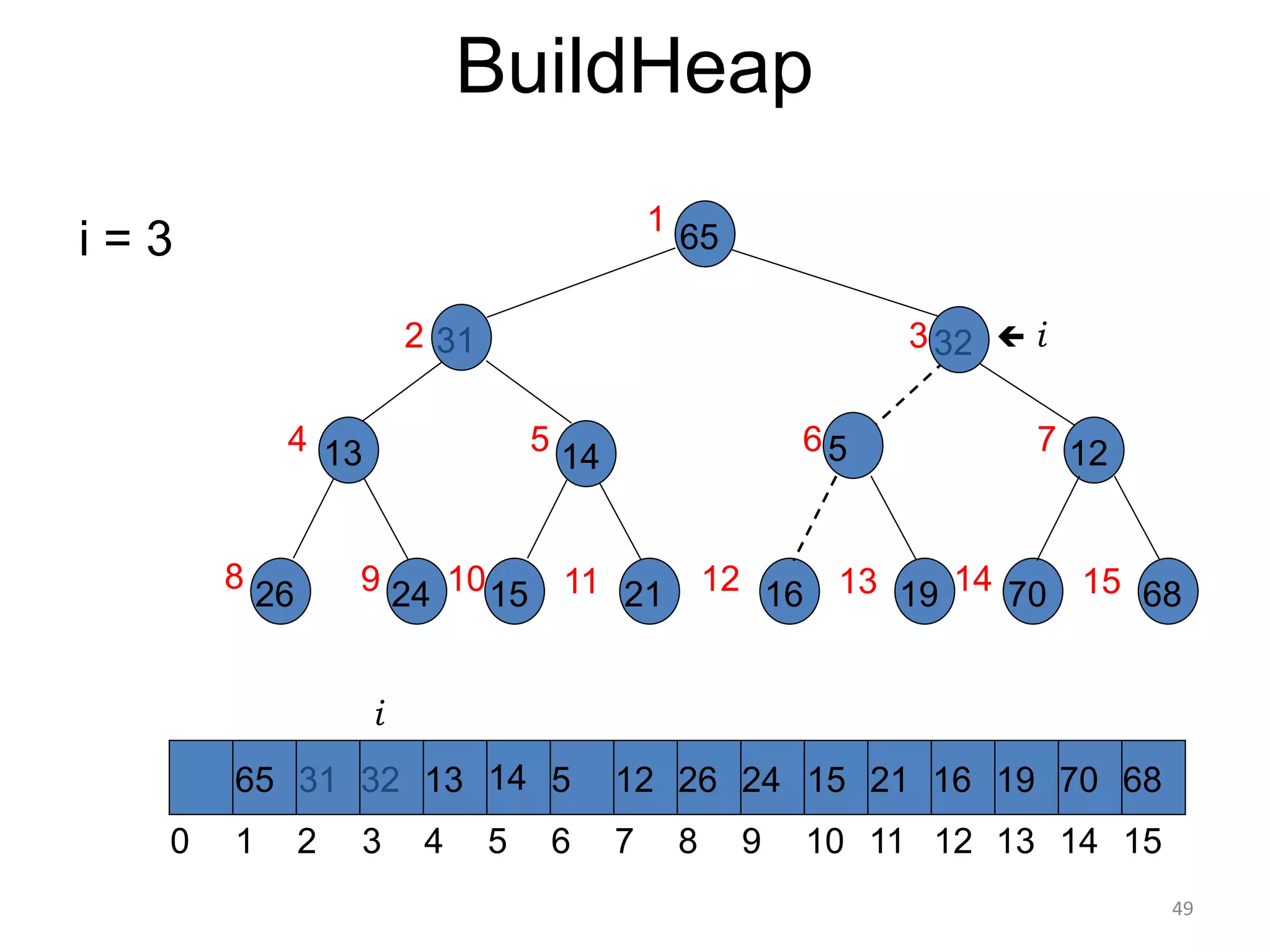
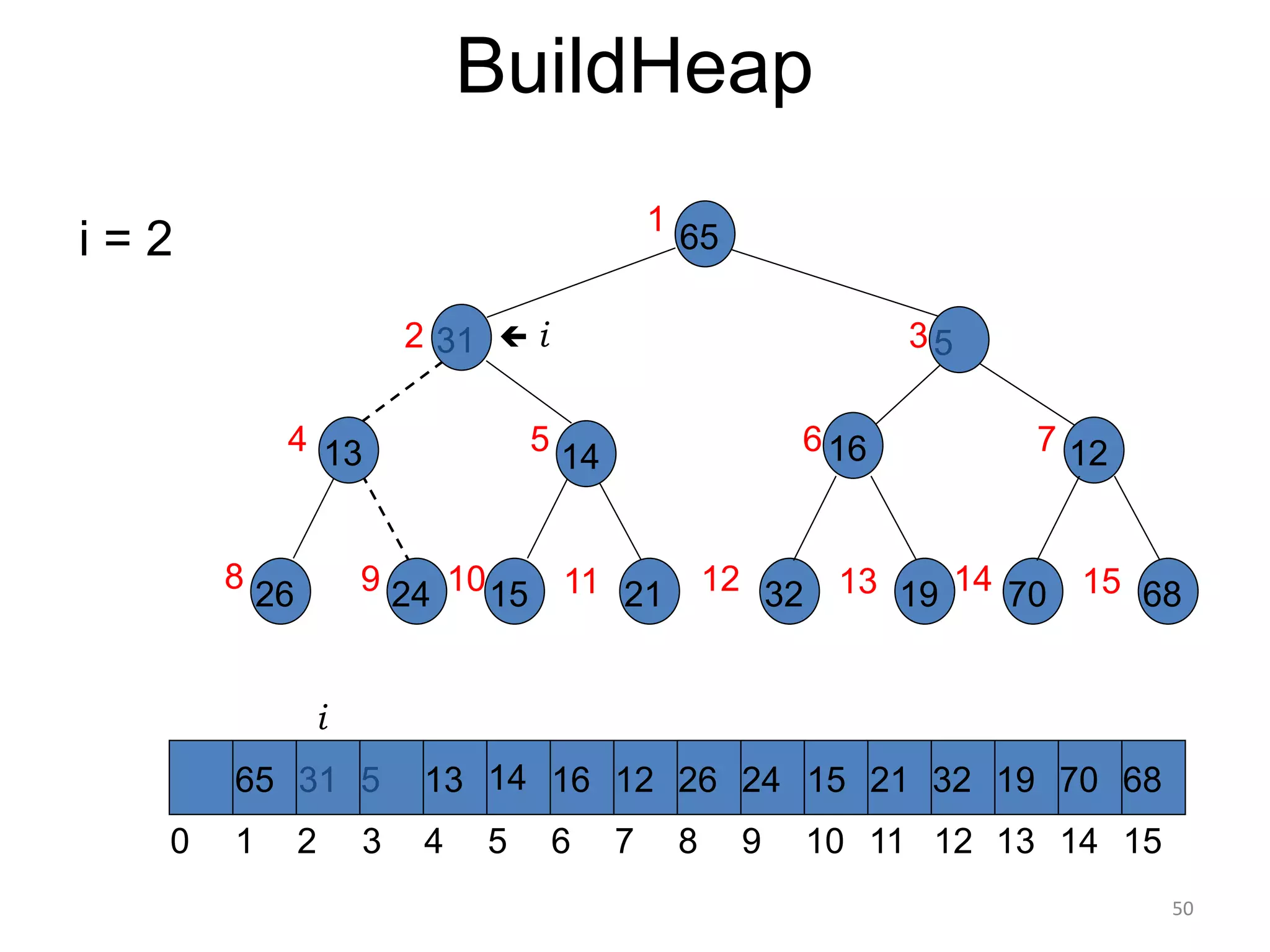
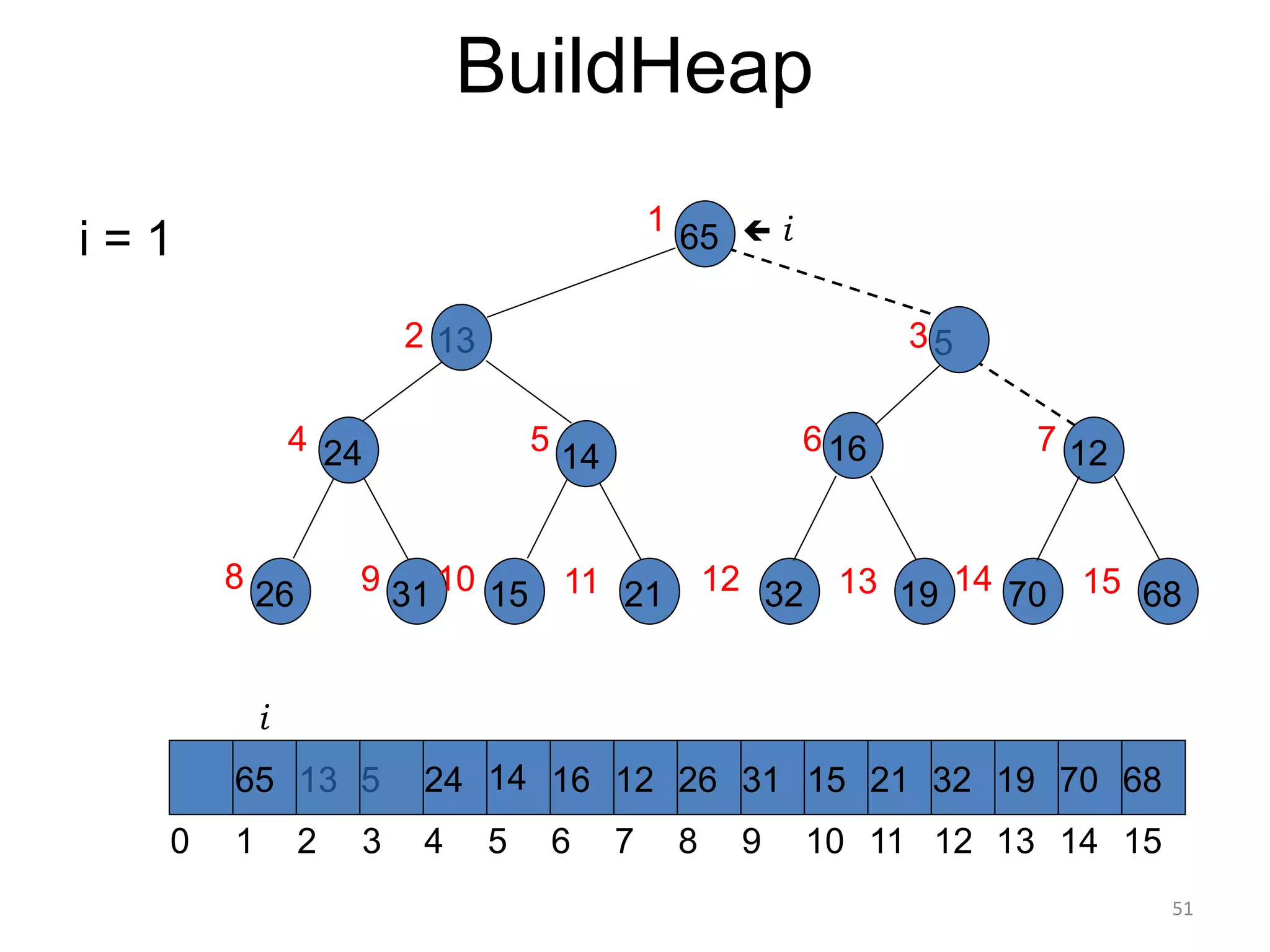
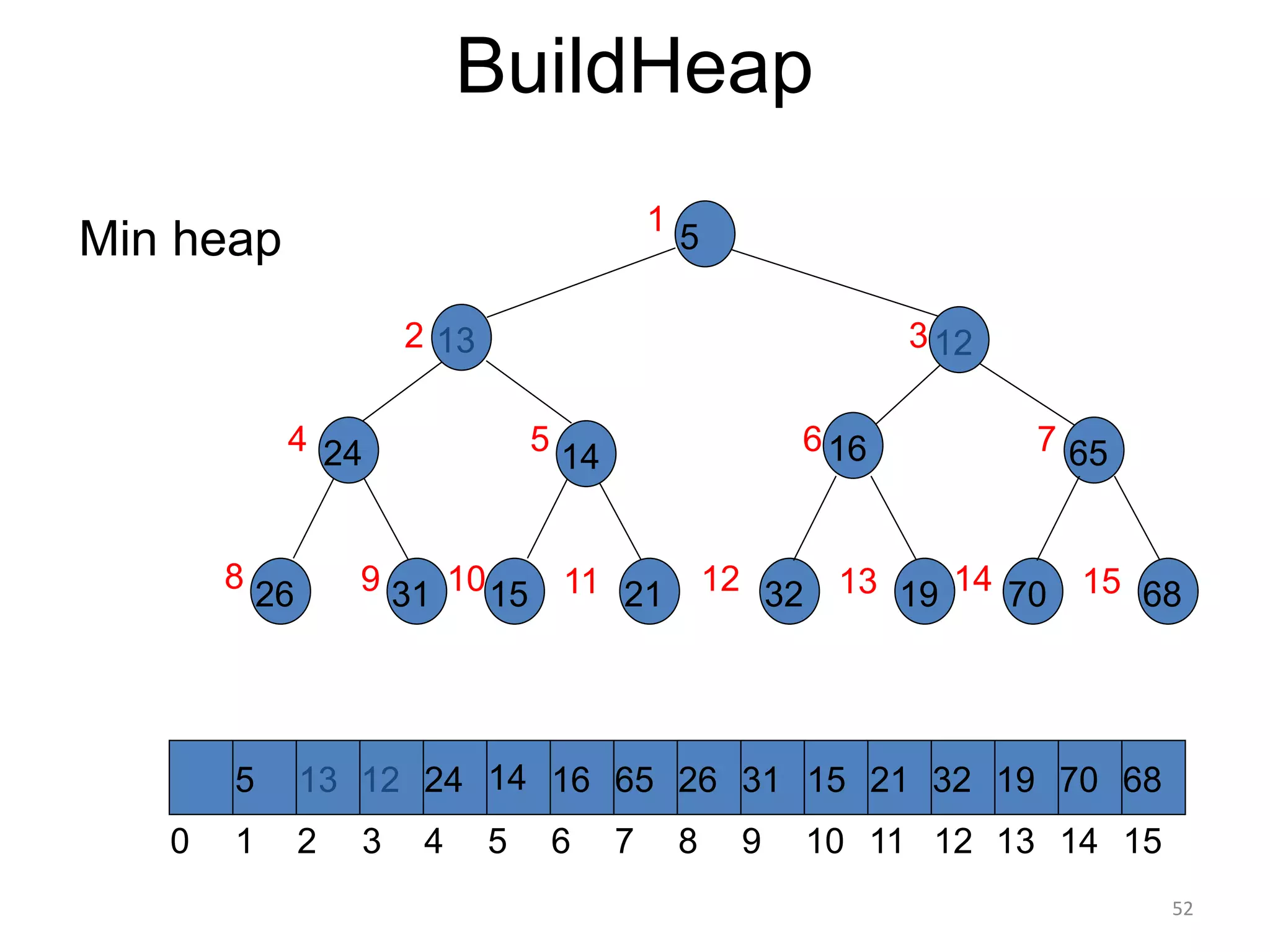
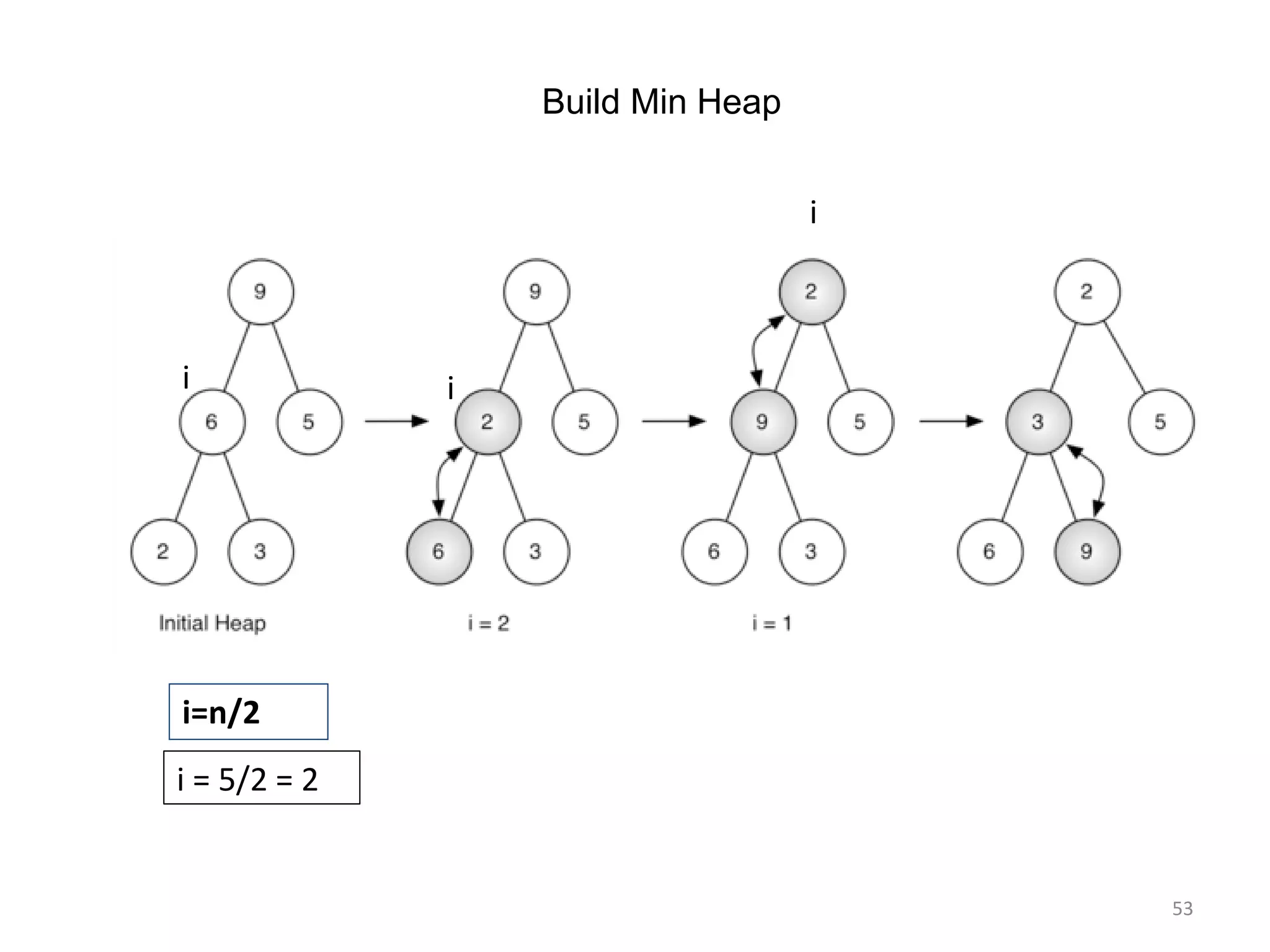
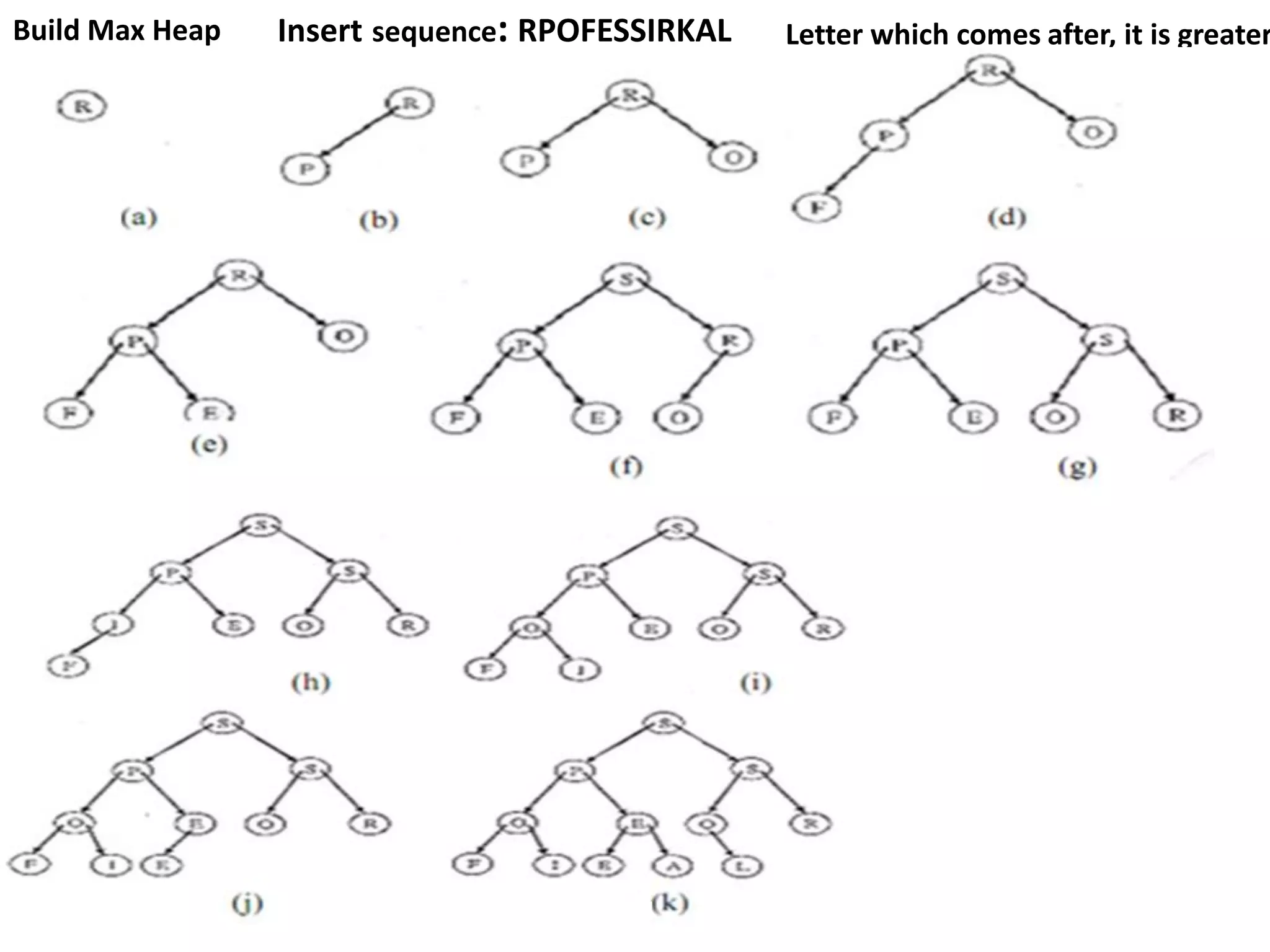
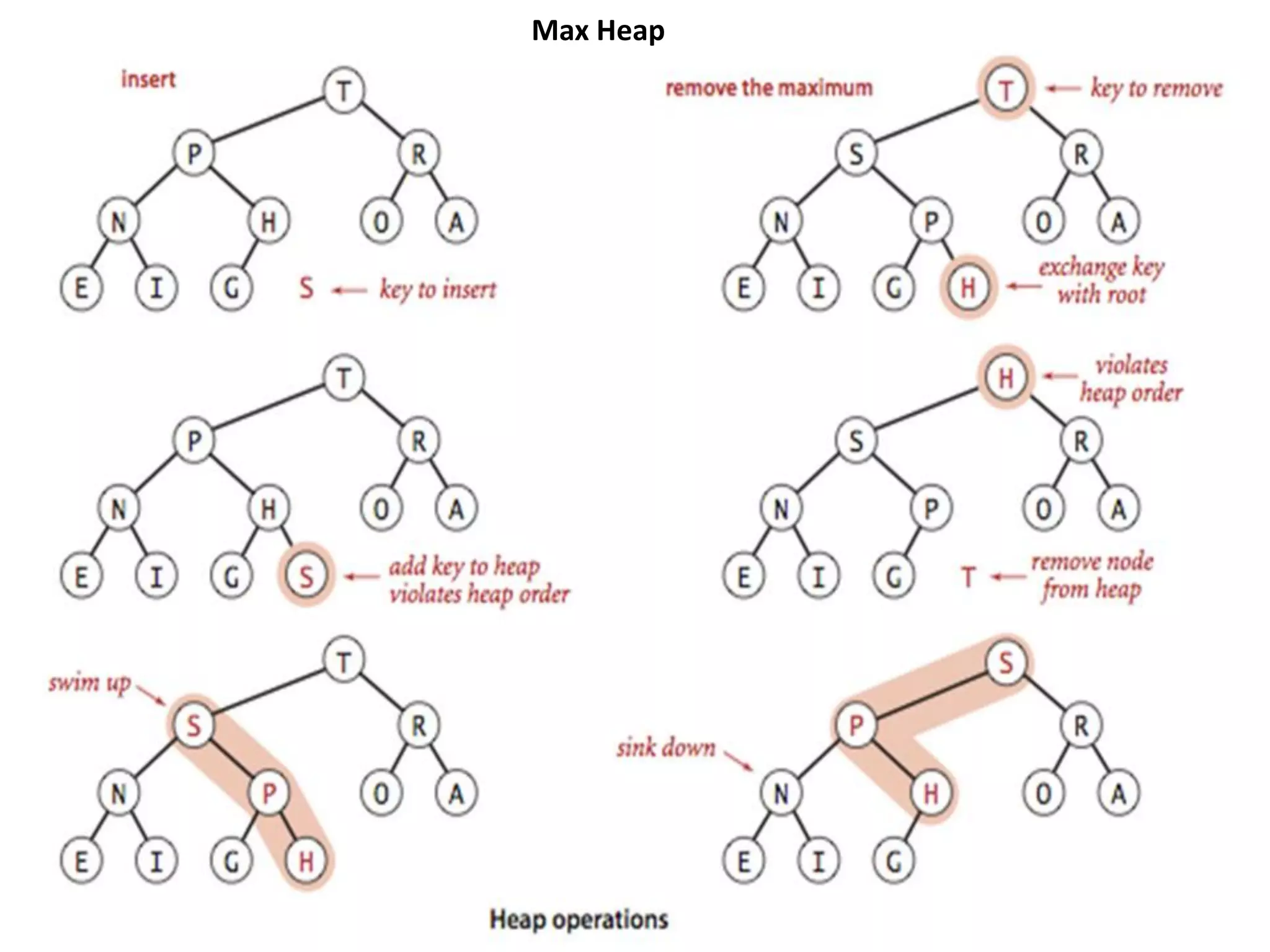
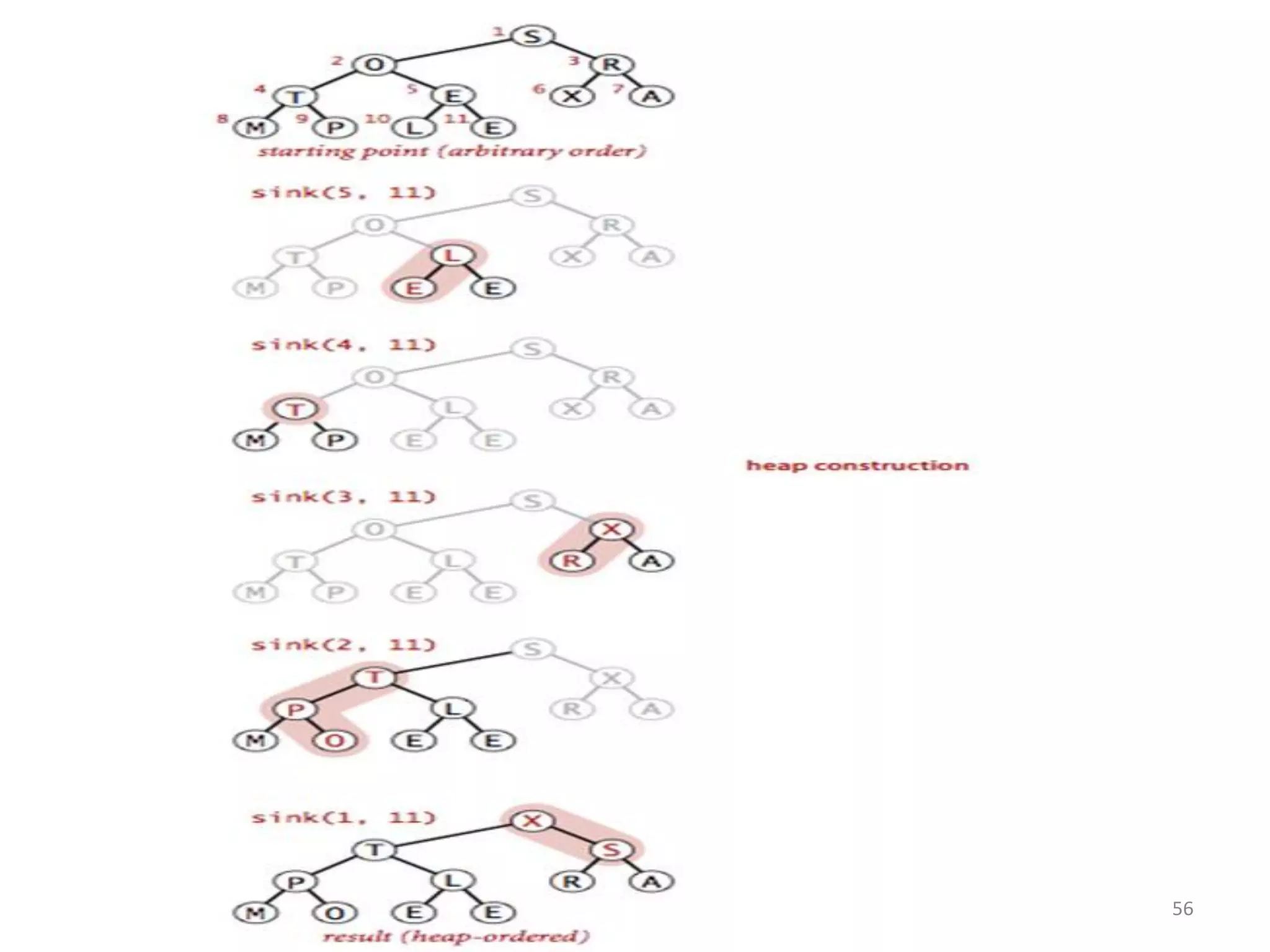
The document discusses binary heaps and algorithms for building, inserting, and deleting elements from heaps. It begins by defining min-heaps and max-heaps, and the heap property that parent nodes are smaller than child nodes in min-heaps and larger in max-heaps. It then covers algorithms for inserting new elements by placing them at the bottom and bubbling up, deleting the minimum/maximum element by replacing it with the last element and bubbling down. The document concludes by explaining that building a heap from a list of elements can be done in linear time by placing elements in an array and percolating them down level-by-level.

1. Data Structures & Algorithm
CS-102
Lecture 8
Binary Heaps
A priority Queue Data Structures
Lecturer: Syeda Nazia Ashraf
1

2. 2
Heap
• A heap is a complete binary tree that
conforms to the heap order.
• The heap order property: in a (min)
heap, for every node X, the key in the
parent is smaller than (or equal to) the key
in X.
• Or, the parent node has key smaller than
or equal to both of its children nodes.

3. 3
Heap
• Analogously, we can define a max-heap,
where the parent has a key larger than the
its two children.
• Thus the largest key would be in the root.

4. 4

5. 5
Heap
13
16
21
31
26
24
65 32
68
19
This is a min
heap

6. 6
Heap
Not a heap: (min)heap property violated
13
19
21
31
26
6
65 32
68
16


19>16
6<21

7. 7
Make Min Heap
Pushdown(6,10)
Pushdown(7,10)

8. 8
Make Max Heap

9. 9
Inserting into a Heap
13
16
21
31
26
24
65 32
68
19
13 21 16 24 31 19 68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
This is an existing heap

10. 10
Inserting into a Heap
insert(14) 13
16
21
31
26
24
65 32
68
19
13 21 16 24 31 19 68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
14
14
11

11. 11
Inserting into a Heap
insert(14) 13
16
21
31
26
24
65 32
68
19
13 21 16 24 31 19 68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10 11

12. 12
Inserting into a Heap
insert(14) 13
16
21
31
26
24
65 32
68
19
13 21 16 24 31
19 68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10 11

13. 13
Inserting into a Heap
insert(14) 13
16
21
31
26
24
65 32
68
19
13 21
16 24 31
19 68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10 11

14. 14
Inserting into a Heap
insert(14) 13
16
21
31
26
24
65 32
68
19
13 21
16 24 31
19 68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10 11
14
14

15. 15
Inserting into a Heap
insert(14) with
exchange
13
16
21
31
26
24
65 32
68
19
13 21 16 24 31 19 68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
14
14
11

16. 16
Inserting into a Heap
insert(14) with
exchange
13
16
21
31
26
24
65 32
68
19
13 21 16 24 31
19 68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
14
14
11

17. 17
Inserting into a Heap
insert(14) with
exchange
13
16
21
31
26
24
65 32
68
19
13 21
16 24 31
19 68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
14
14
11

18. 18
Inserting into a Heap
insert(15) with
exchange
13
16
21
31
26
24
65 32
68
19
13 21
16 24 31
19 68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
14
14
11
15
15
12

19. 19
Inserting into a Heap
insert(15) with
exchange
13
16
21
31
26
24
65 32
68
19
13 21
16 24 31 19
68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
14
14
11
15
15
12

20. 20
Inserting into a Heap
insert(15) with
exchange
13
16
21
31
26
24
65 32
68
19
13 21 16
24 31 19
68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
14
14
11
15
15
12

21. 21
Inserting into a Heap
insert(15) with
exchange
13
16
21
31
26
24
65 32
68
19
13 21 16
24 31 19
68 65 26 32
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
14
14
11
15
15
12

22. Inserting into a Heap
22
Max Heap
To add an item to a heap, we follow the reverse procedure. Place it in the next
leaf position and move it up.
Again, we require O(h) or O(logn) exchanges.

23. 23
P<X
N<X

24. 24
T<X

25. 25
Insert in Min Heap

26. 26
Insert in Max Heap

27. 27
DeleteMin
• Deletion in Max (or Min) Heap always happens at the root
to remove the Maximum (or minimum) value.
• Deleting it (or removing it) from root causes a hole which
needs to be filled.
13
16
21
31
26
24
65 32
68
19
1
2 3
7
6
5
4
8 9 10
14
11

28. 28
DeleteMin
deleteMin()
16
21
31
26
24
65 32
68
19
1
2 3
7
6
5
4
8 9 10
14
11

29. 29
DeleteMin
deleteMin()
14
16
21
31
26
24
65 32
68
19
1
2 3
7
6
5
4
8 9 10 11

30. 30
DeleteMin
deleteMin()
14
16
31
26
24
65 32
68
19
1
2 3
7
6
5
4
8 9 10
21
11

31. 31
DeleteMin
deleteMin()
14
16
31
26
24
65 32
68
19
1
2 3
7
6
5
4
8 9 10
21
11

32. 32
DeleteMin
deleteMin(): heap size is reduced by 1.
14
16
31
26
24
65 32
68
19
1
2 3
7
6
5
4
8 9 10
21

33. DeleteMin
33

34. 34

35. 35
DelMin

36. Let's start with this heap. A
deletion will remove the T
at the root.
To work out how we're going
to maintain the heap property,
use the fact that a complete
tree is filled from the left. So
that the position which must
become empty is the one
occupied by the M. Put it in
the vacant root position.
DeleteMax
36

37. This has violated the condition
that the root must be greater
than each of its children. So
interchange the M with the
larger of its children.
The left subtree has now lost
the heap property. So again
interchange the M with the
larger of its children.
This tree is now a heap
again, so we're finished.
DeleteMax
We need to make at most h interchanges of a root of a subtree with one of its children to
fully restore the heap property. Thus deletion from a heap is O(h) or O(logn).
37

38. 38
BuildHeap
• Suppose we are given as input N keys (or
items) and we want to build a heap of the
keys.
• Obviously, this can be done with N
successive inserts.
• Each call to insert will either take unit time
(leaf node) or log2N (if new key percolates
all the way up to the root).

39. 39
BuildHeap
• The worst time for building a heap of N
keys could be Nlog2N.
• It turns out that we can build a heap in
linear time.

40. 40
BuildHeap
• Suppose we have a method
percolateDown(p) which moves down the
key in node p downwards.
• This is what was happening in deleteMin.

41. 41
BuildHeap
Initial data (N=15)
65 21 19
26 14 16
68 13 24 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
31 32
15
4
5 70 12

42. 42
BuildHeap
Initial data (N=15) 65
19
21
14
24
26
13 15
68
16
65 21 19
26 14 16
68 13 24 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
31
31
11
32
32
12
15
4
5
13 70
14 12
15
5 70 12

43. 43
BuildHeap
• The general algorithm is to place the N
keys in an array and consider it to be an
unordered binary tree.
• The following algorithm will build a heap
out of N keys.
for( i = N/2; i > 0; i-- )
percolateDown(i);

44. 44
BuildHeap
i = 15/2 = 7 65
19
21
14
24
26
13 15
68
16
65 21 19
26 14 16
68 13 24 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
31
31
11
32
32
12
15
4
5
13 70
14 12
15
5 70 12
i
 i
i=n/2
Minimum Heap

45. 45
BuildHeap
i = 15/2 = 7 65
19
21
14
24
26
13 15
12
16
65 21 19
26 14 16
12 13 24 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
31
31
11
32
32
12
15
4
5
13 70
14 68
15
5 70 68
i
 i

46. 46
BuildHeap
i = 6 65
19
21
14
24
26
13 15
12
16
65 21 19
26 14 16
12 13 24 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
31
31
11
32
32
12
15
4
5
13 70
14 68
15
5 70 68
i
 i

47. BuildHeap
i = 5 65
5
21
14
24
26
13 15
12
16
65 21 5
26 14 16
12 13 24 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
31
31
11
32
32
12
15
4
19
13 70
14 68
15
19 70 68
i
 i
47

48. BuildHeap
i = 4 65
5
14
21
24
26
13 15
12
16
65 14 5
26 21 16
12 13 24 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
31
31
11
32
32
12
15
4
19
13 70
14 68
15
19 70 68
i
 i
48

49. BuildHeap
i = 3 65
5
14
21
24
13
26 15
12
16
65 14 5
13 21 16
12 26 24 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
31
31
11
32
32
12
15
4
19
13 70
14 68
15
19 70 68
i
 i
49

50. BuildHeap
i = 2 65
16
14
21
24
13
26 15
12
32
65 14 16
13 21 32
12 26 24 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
31
31
11
5
5
12
15
4
19
13 70
14 68
15
19 70 68
i
 i
50

51. BuildHeap
i = 1 65
16
14
21
31
24
26 15
12
32
65 14 16
24 21 32
12 26 31 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
13
13
11
5
5
12
15
4
19
13 70
14 68
15
19 70 68
i
 i
51

52. BuildHeap
Min heap 5
16
14
21
31
24
26 15
65
32
5 14 16
24 21 32
65 26 31 15
1 2 3 5 6 7 8 9 10 11 12 13 14
0
1
2 3
7
6
5
4
8 9 10
13
13
11
12
12
12
15
4
19
13 70
14 68
15
19 70 68
52

53. 53
Build Min Heap
i
i i
i=n/2
i = 5/2 = 2

54. 54
Build Max Heap Insert sequence: RPOFESSIRKAL Letter which comes after, it is greater

55. 55
Max Heap

56. 56

57. Other Heap Operations
• decreaseKey(p, delta):
lowers the value of the key at position ‘p’ by the
amount ‘delta’. Since this might violate the heap order,
the heap must be reorganized with percolate up (in
min heap) or down (in max heap).
• increaseKey(p, delta):
opposite of decreaseKey.
• remove(p):
removes the node at position p from the heap. This is
done by first decreaseKey(p, delta) and then
performing deleteMin().
57