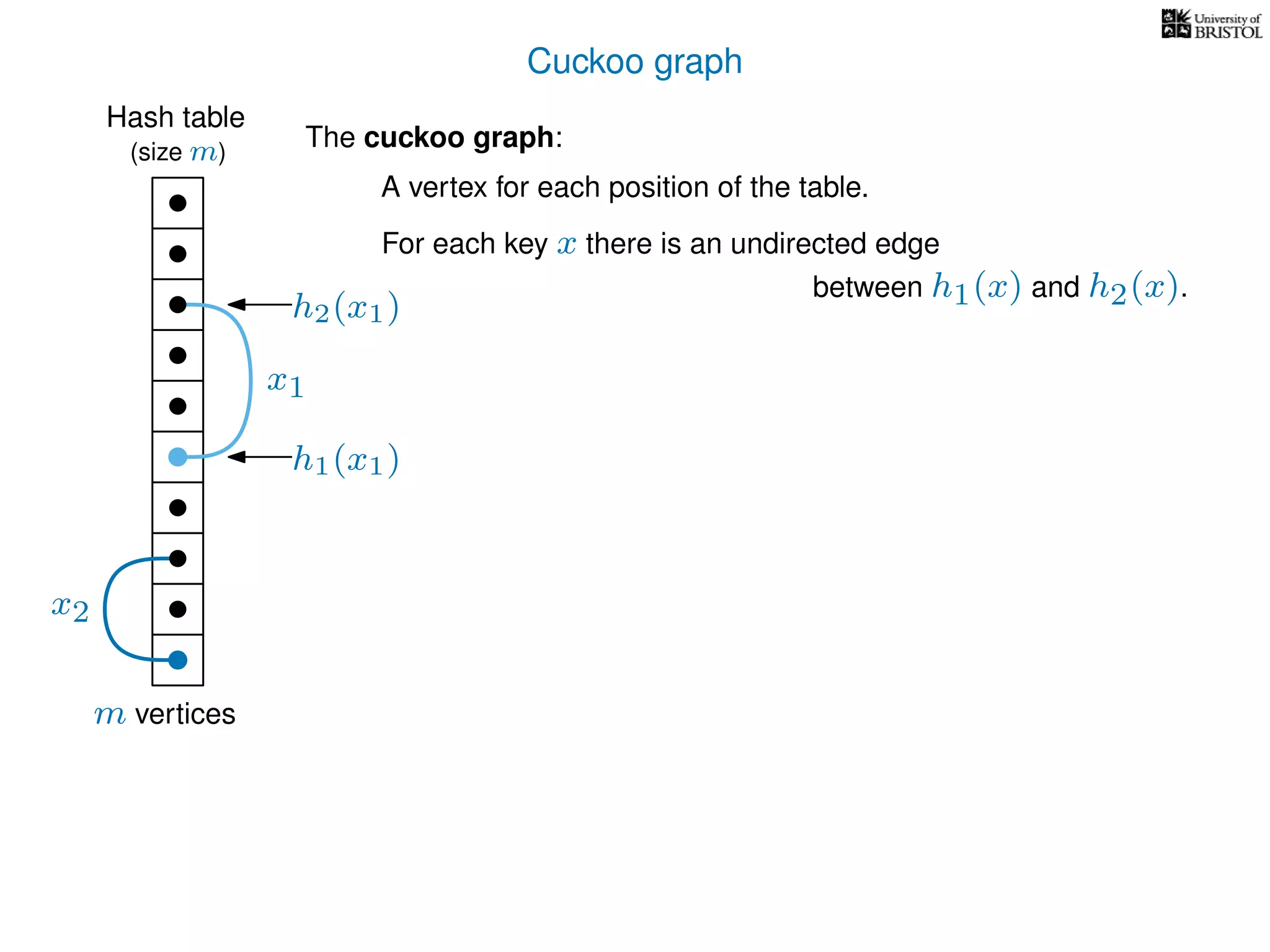
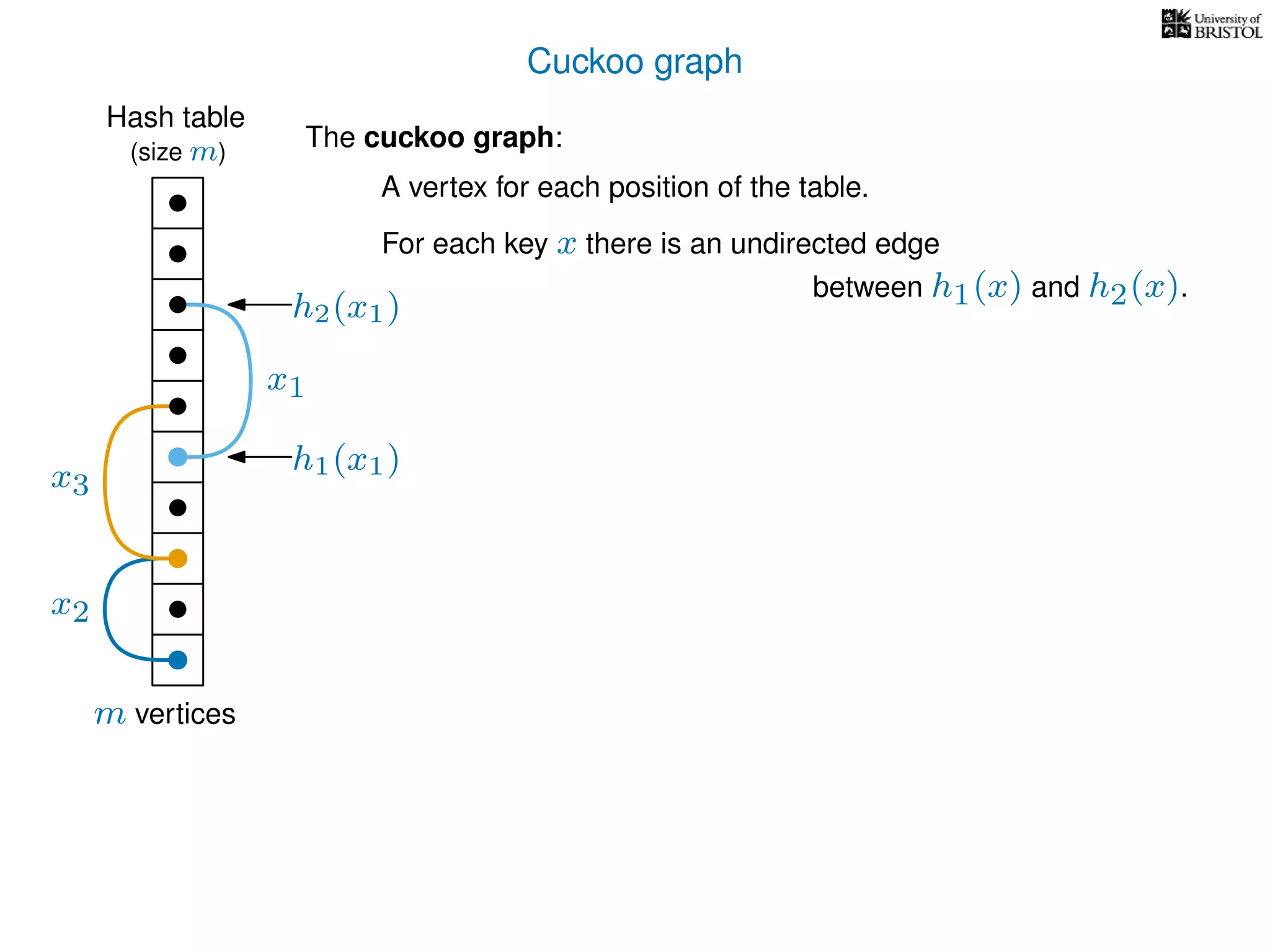
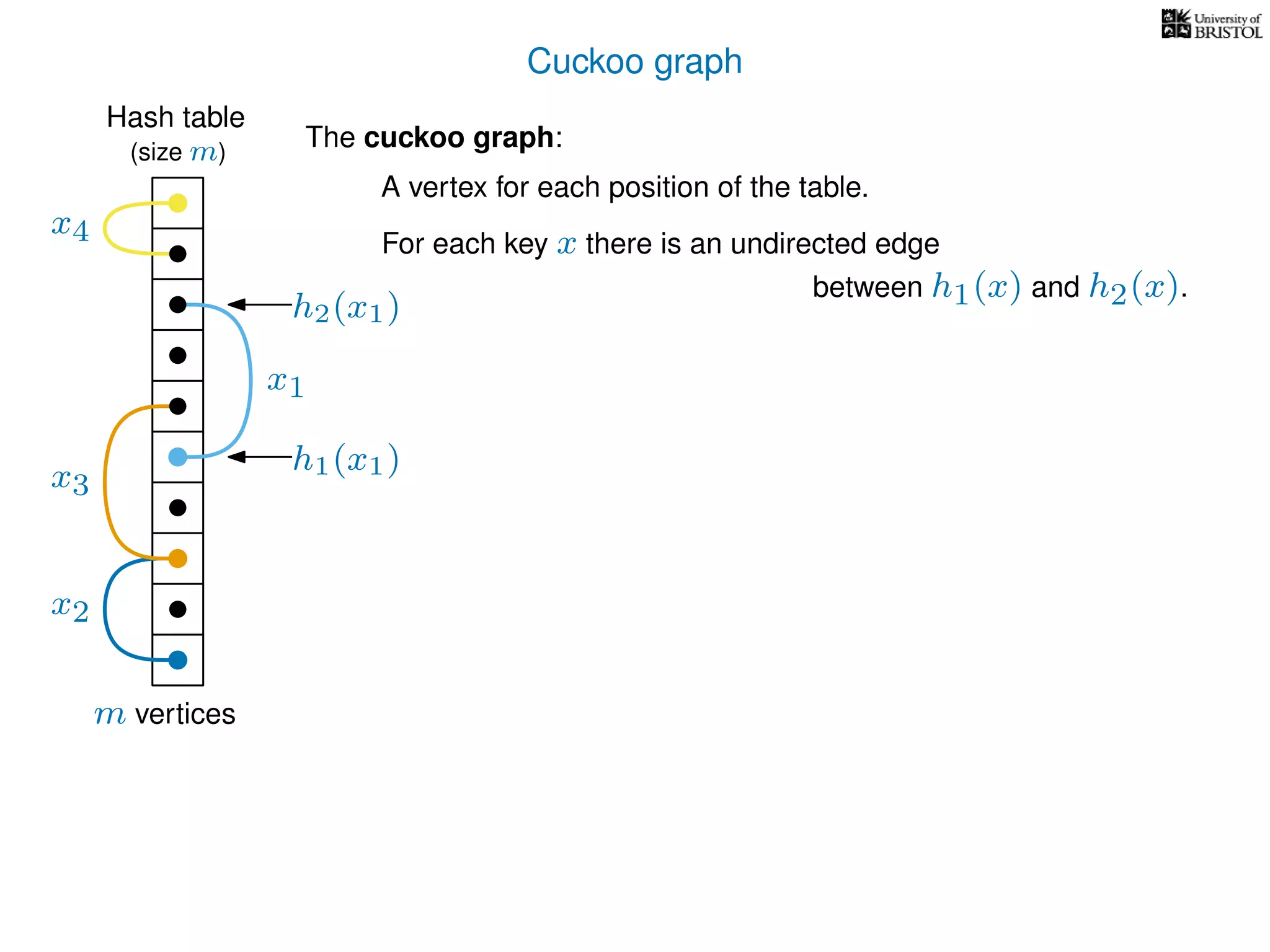
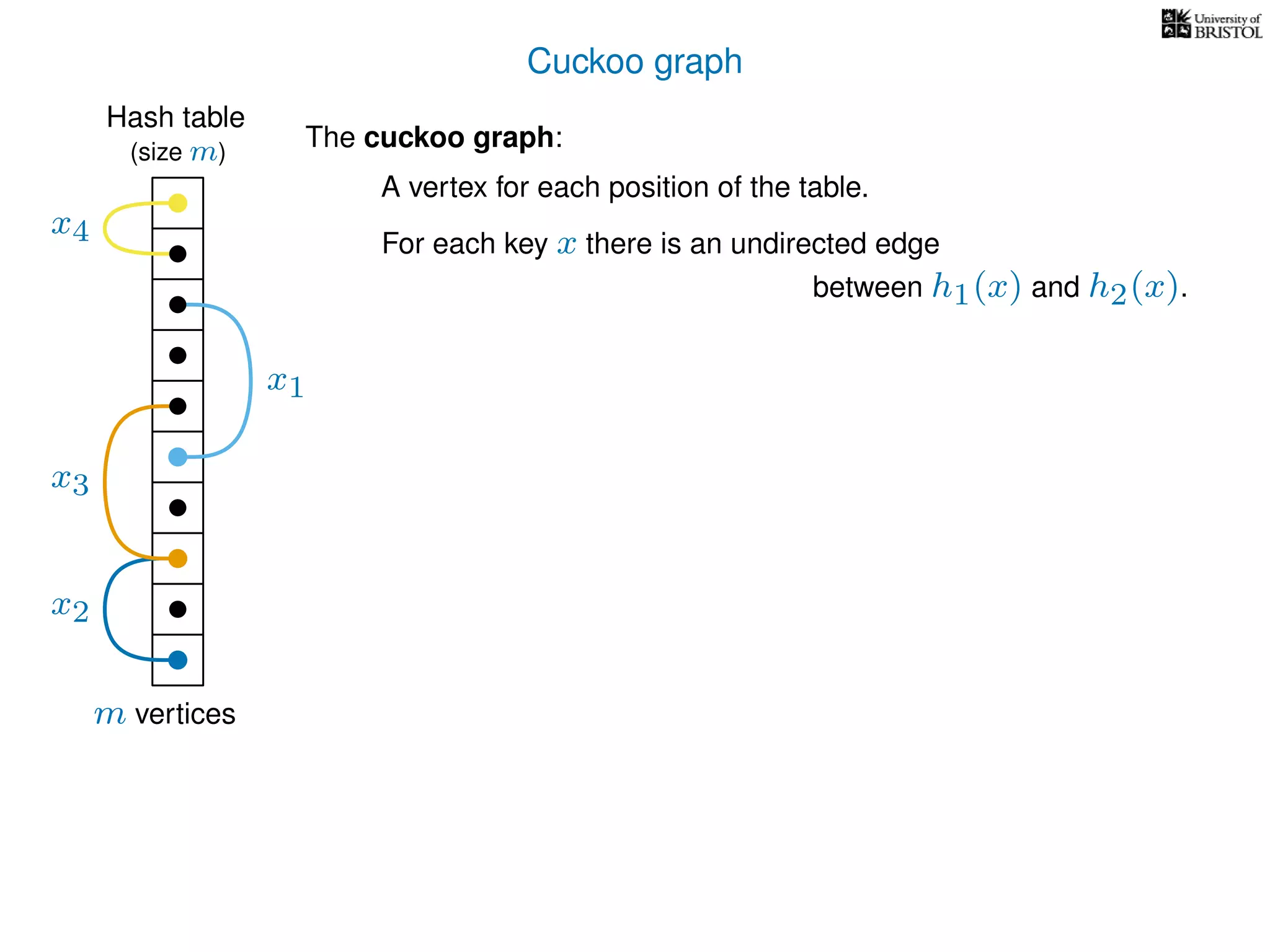
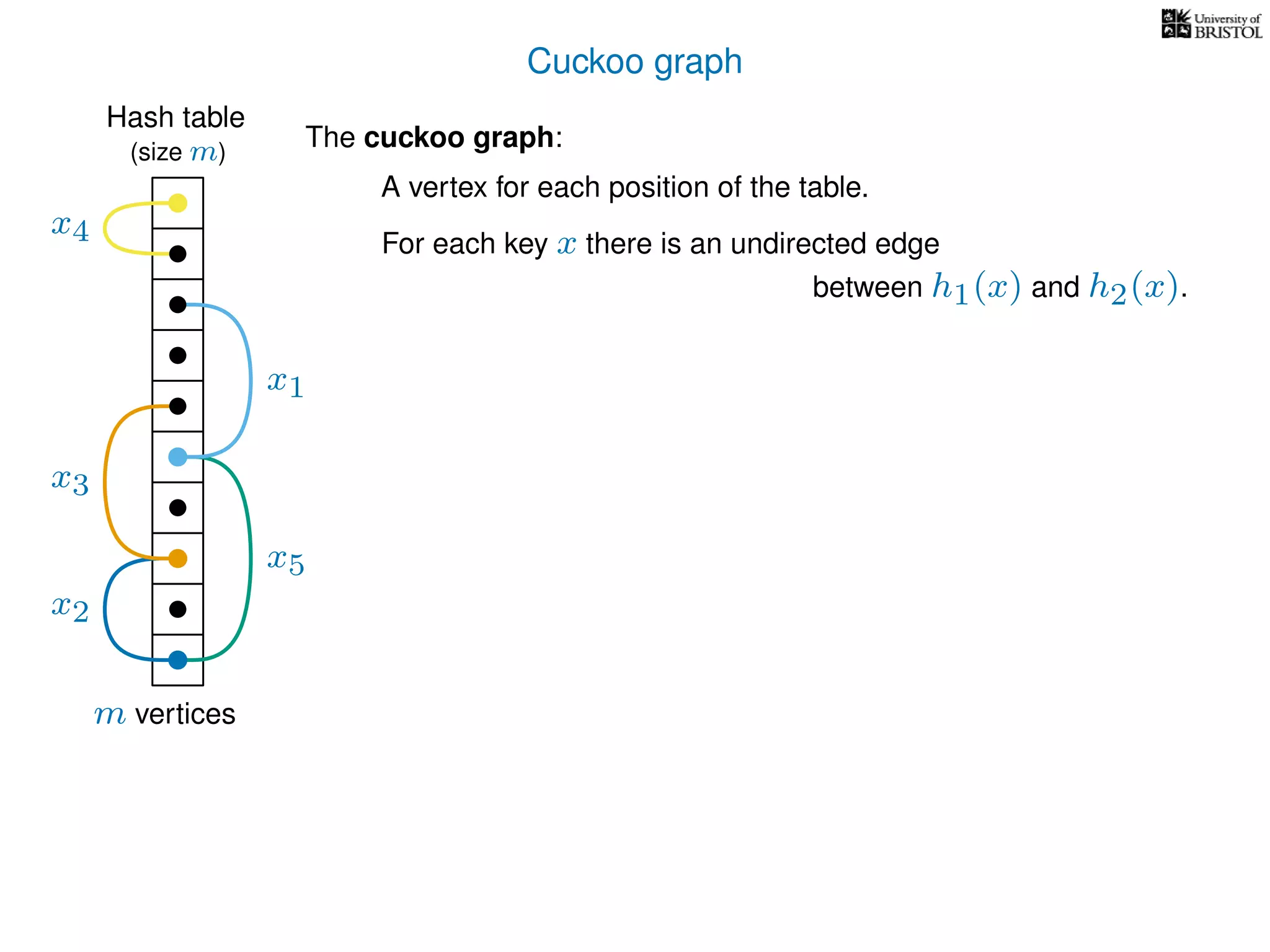
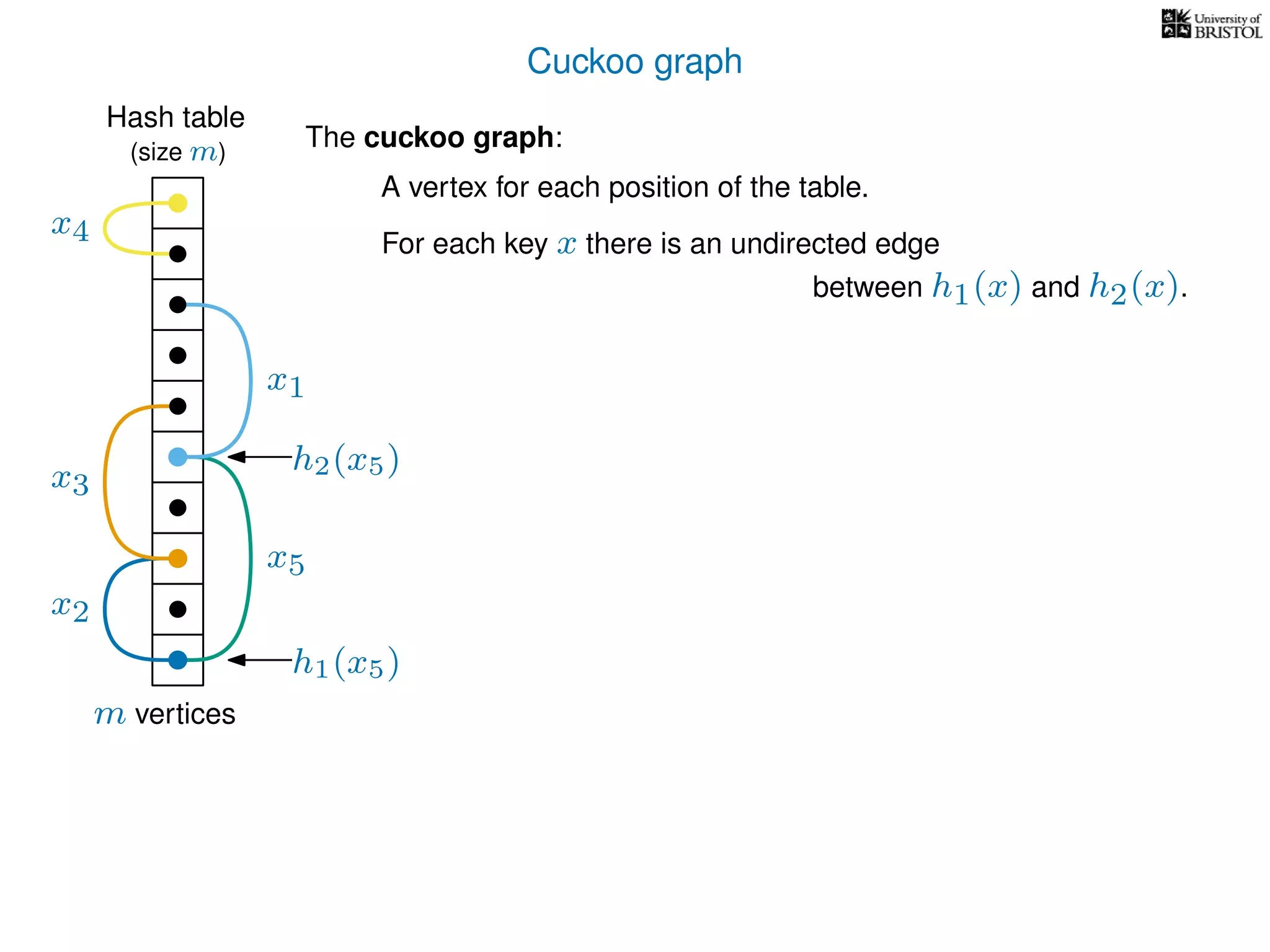
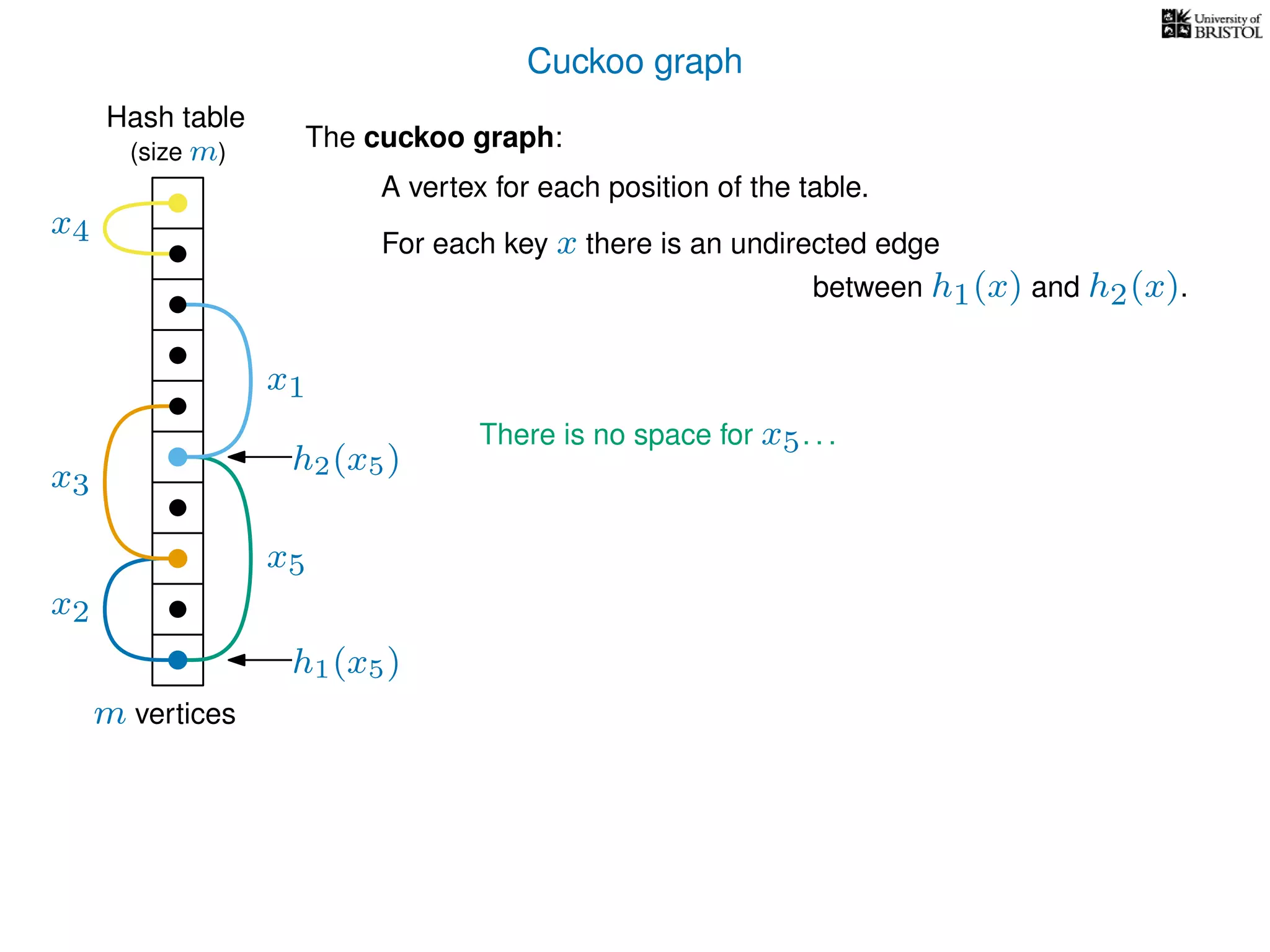
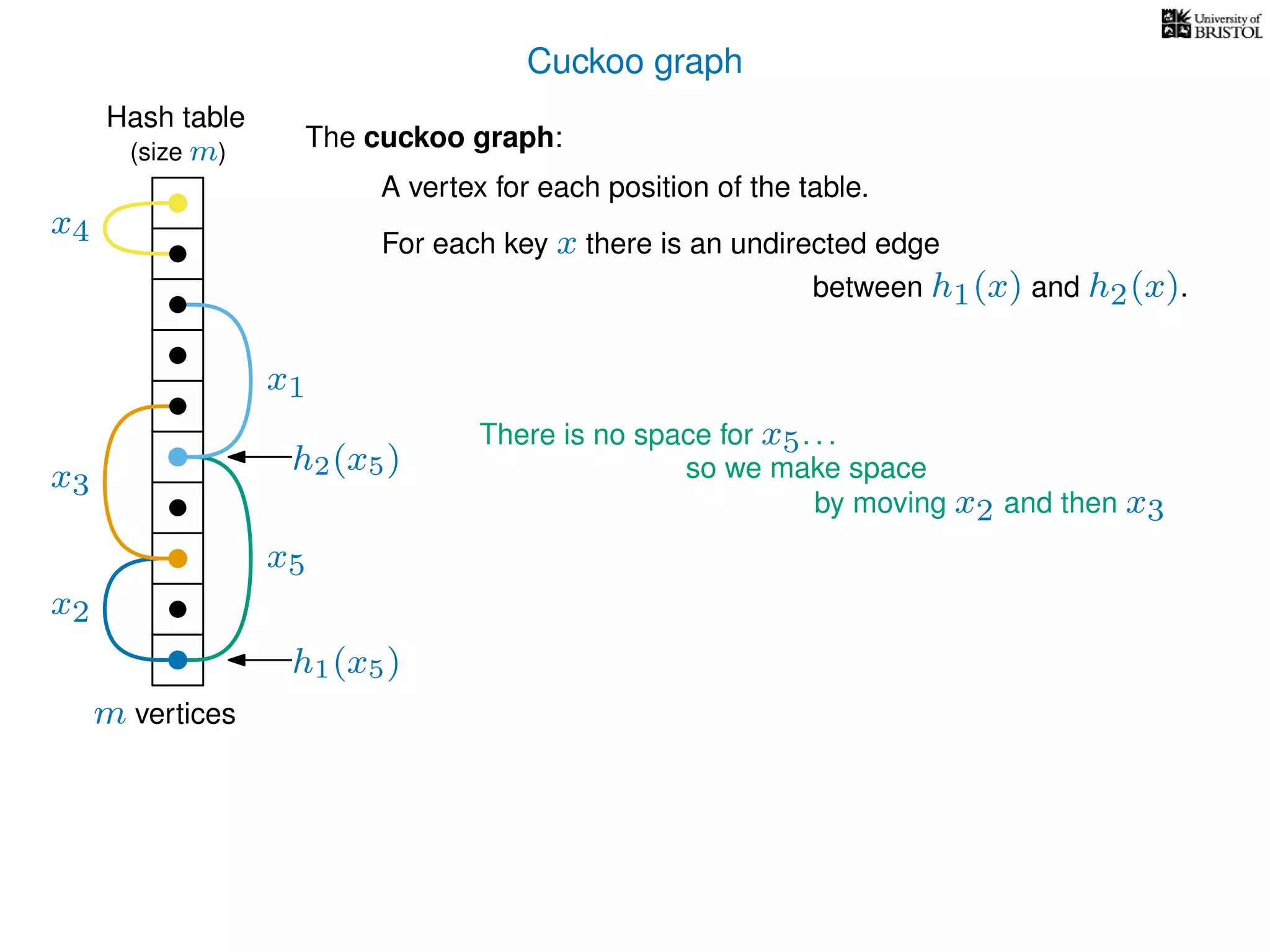
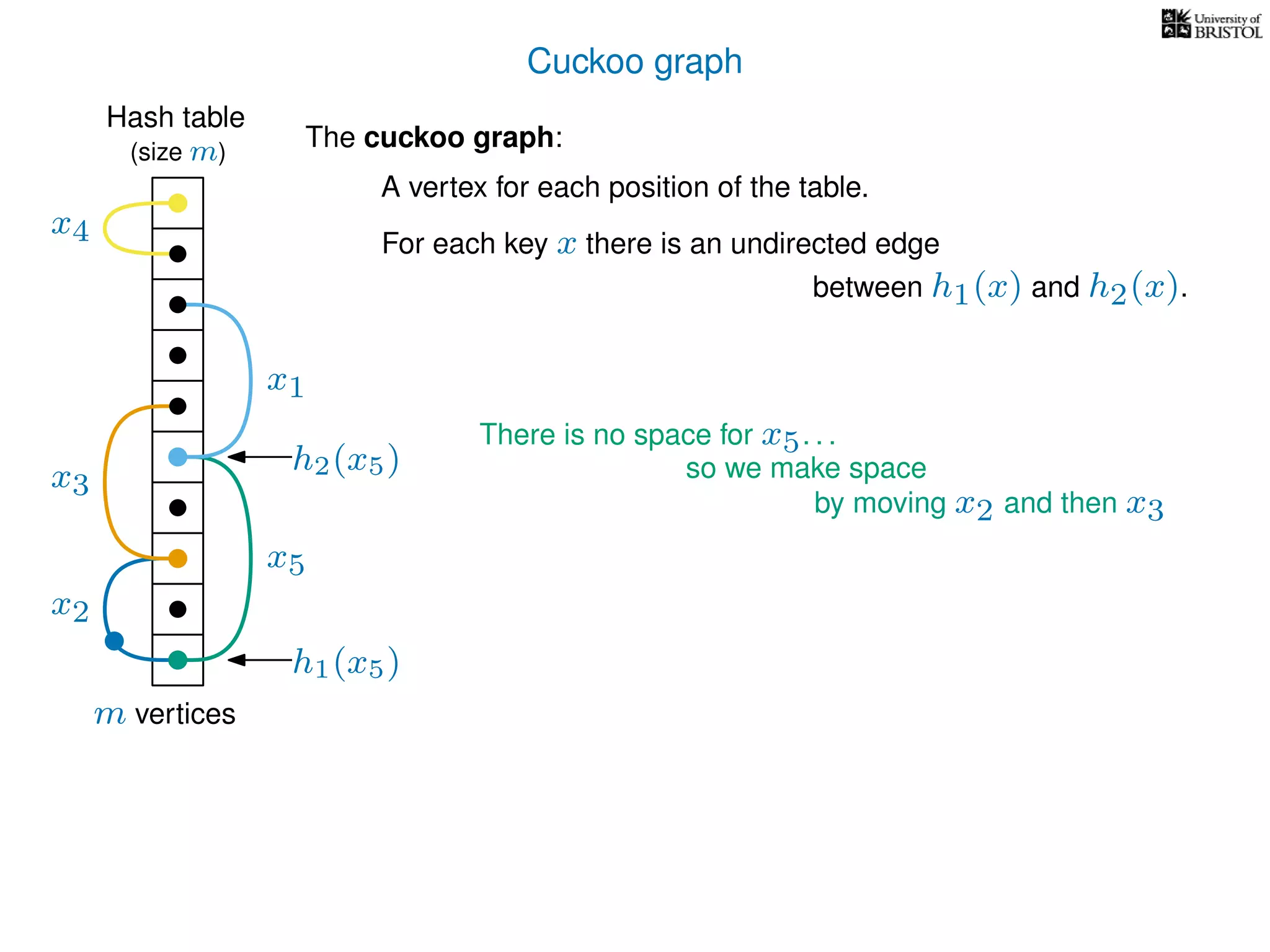
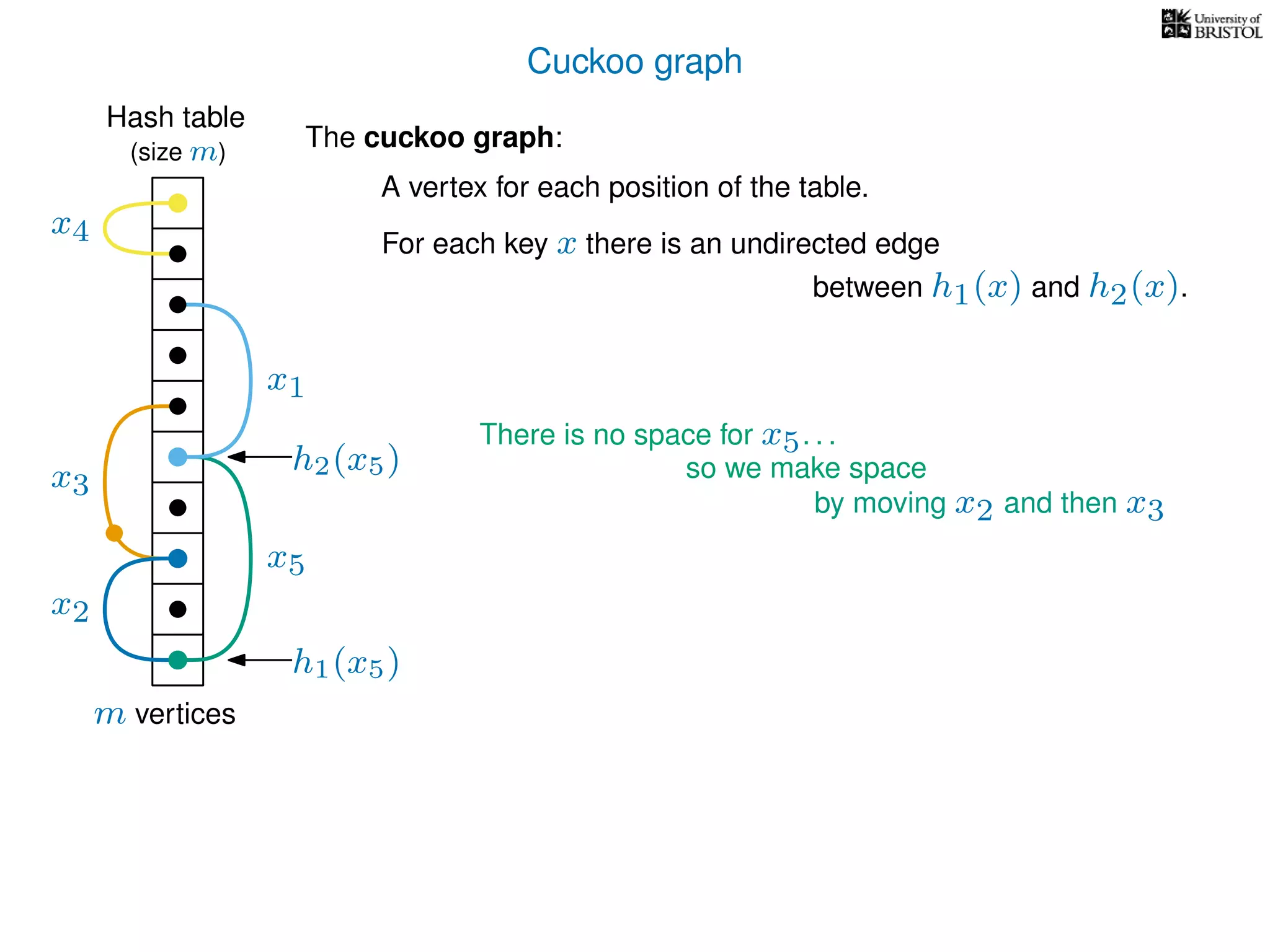
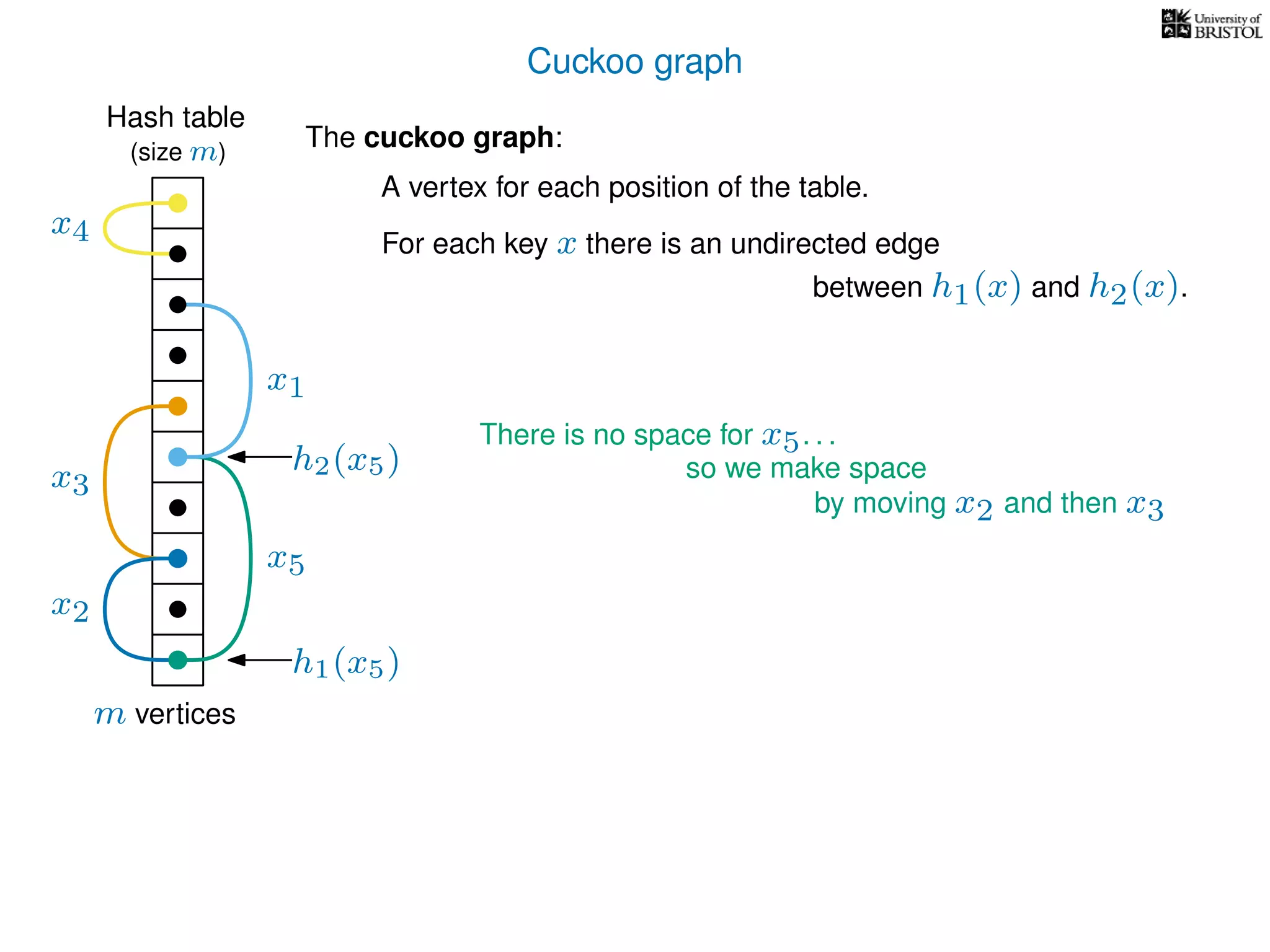
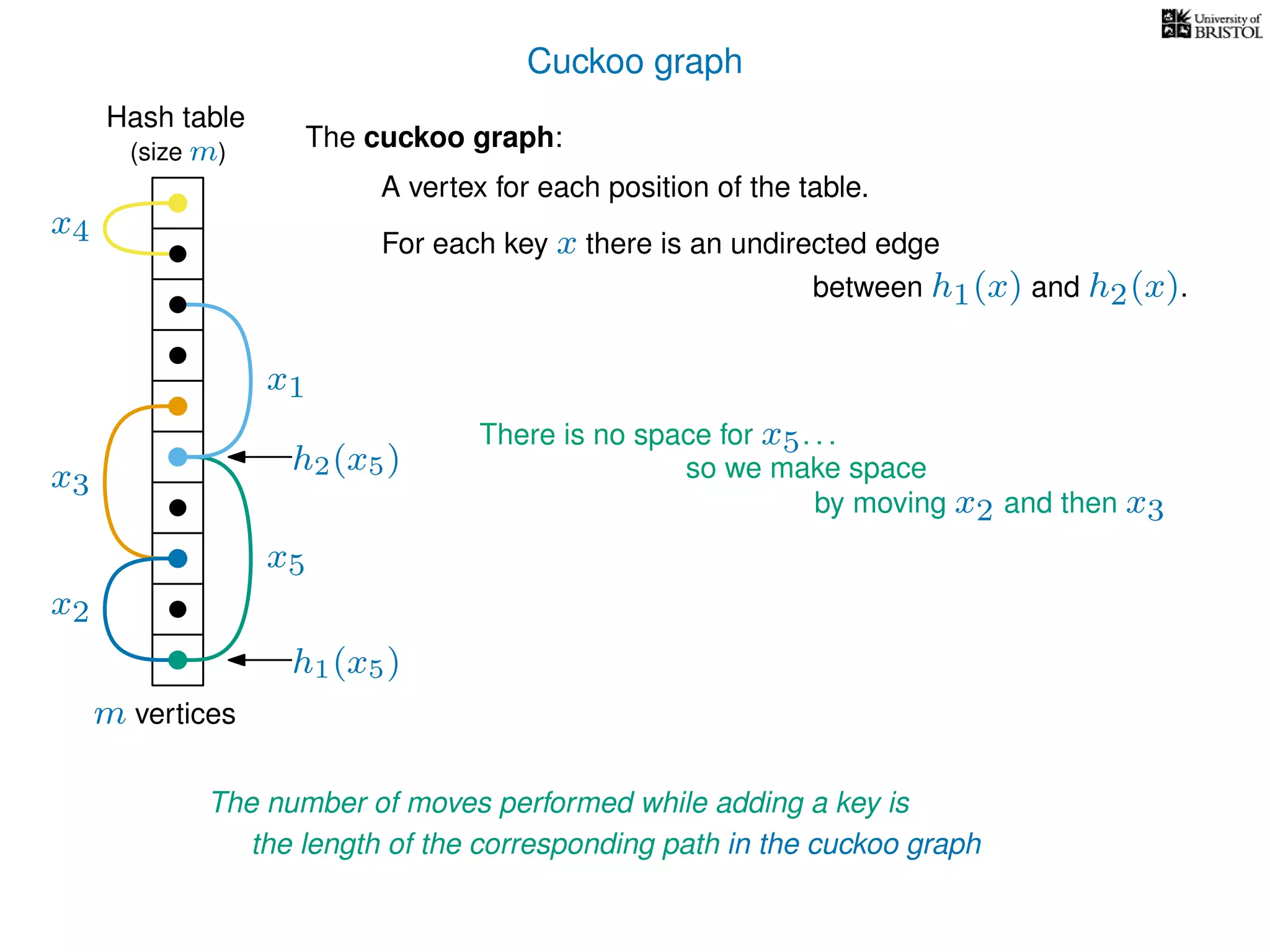
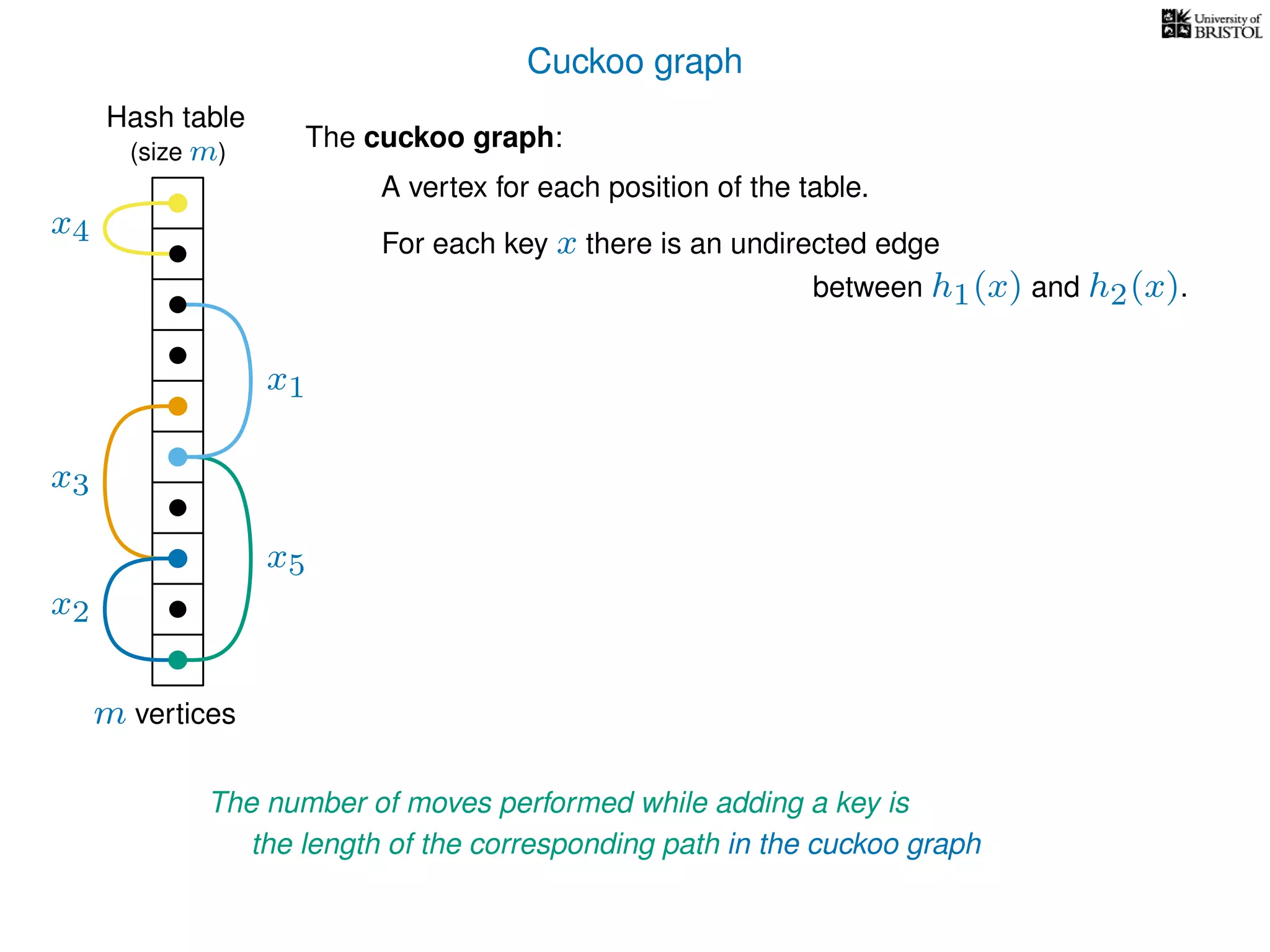
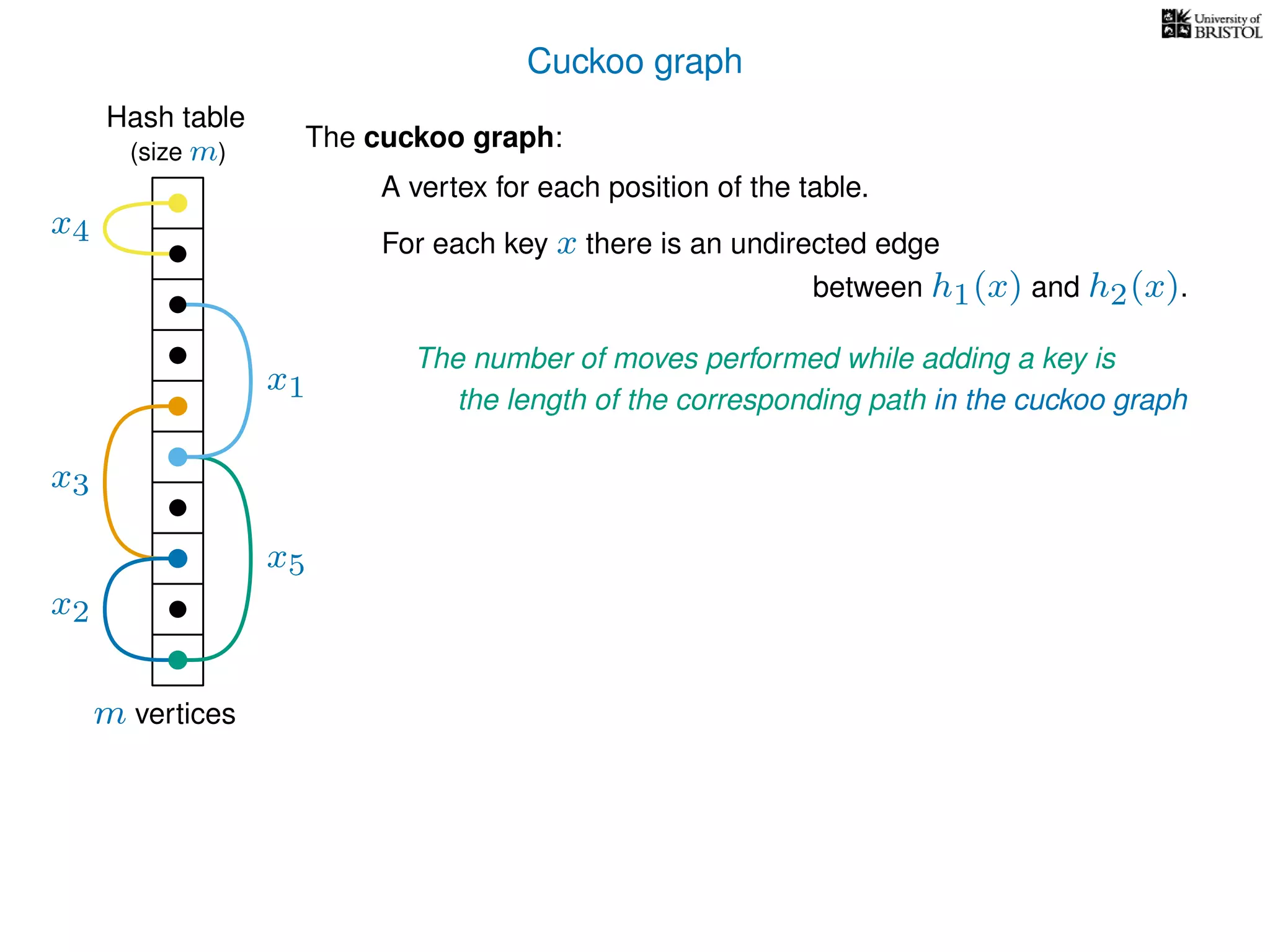
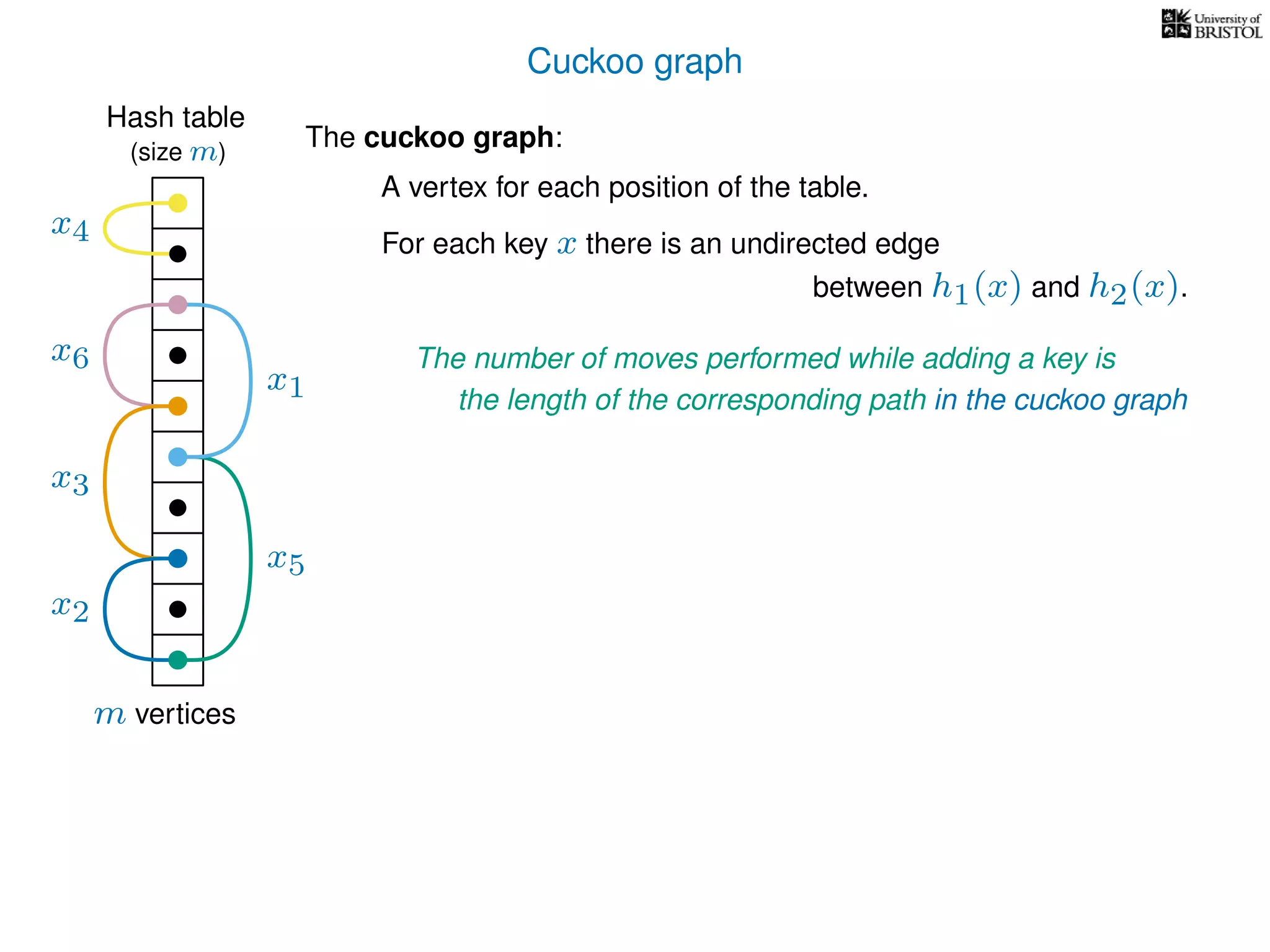
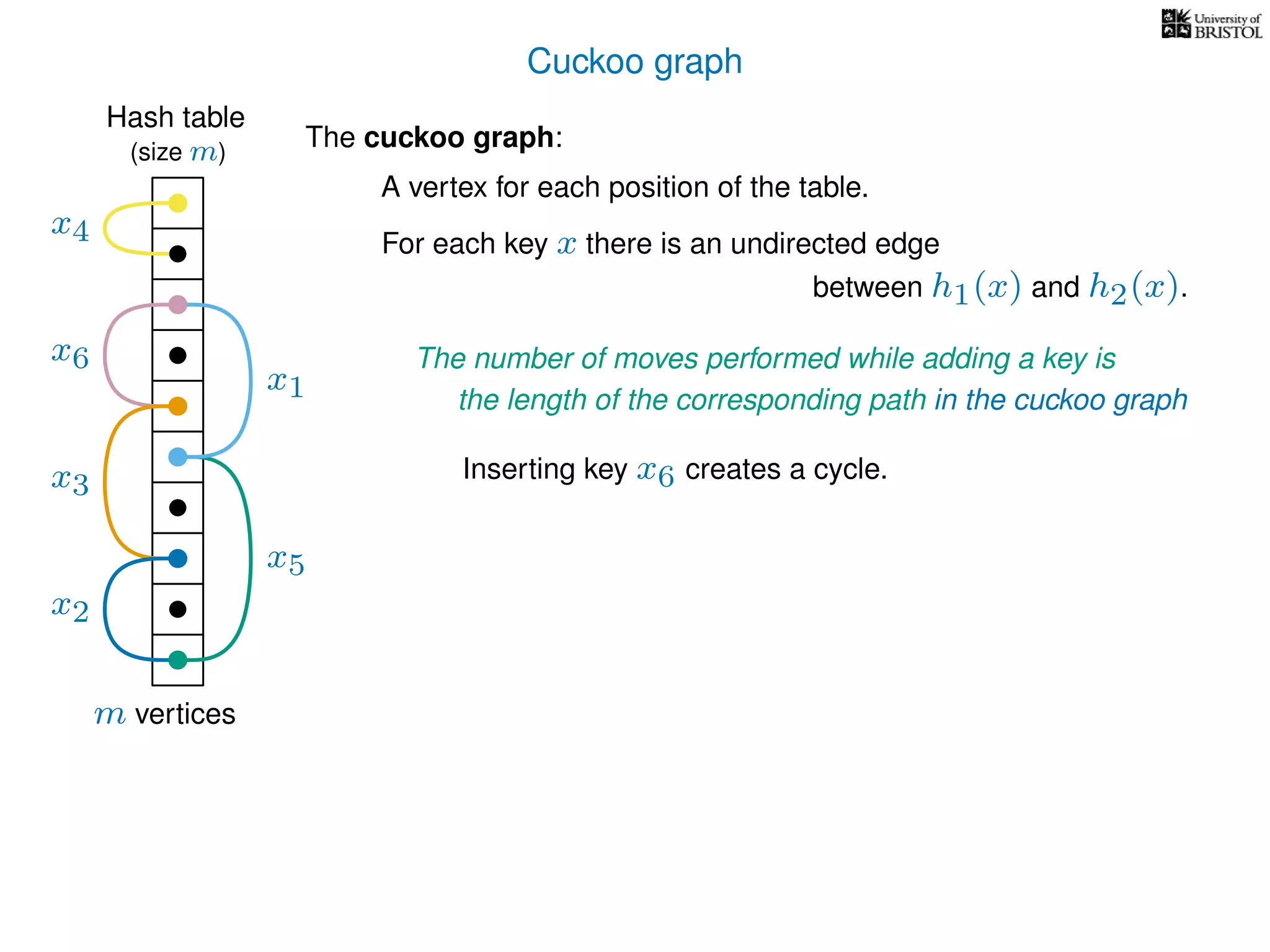
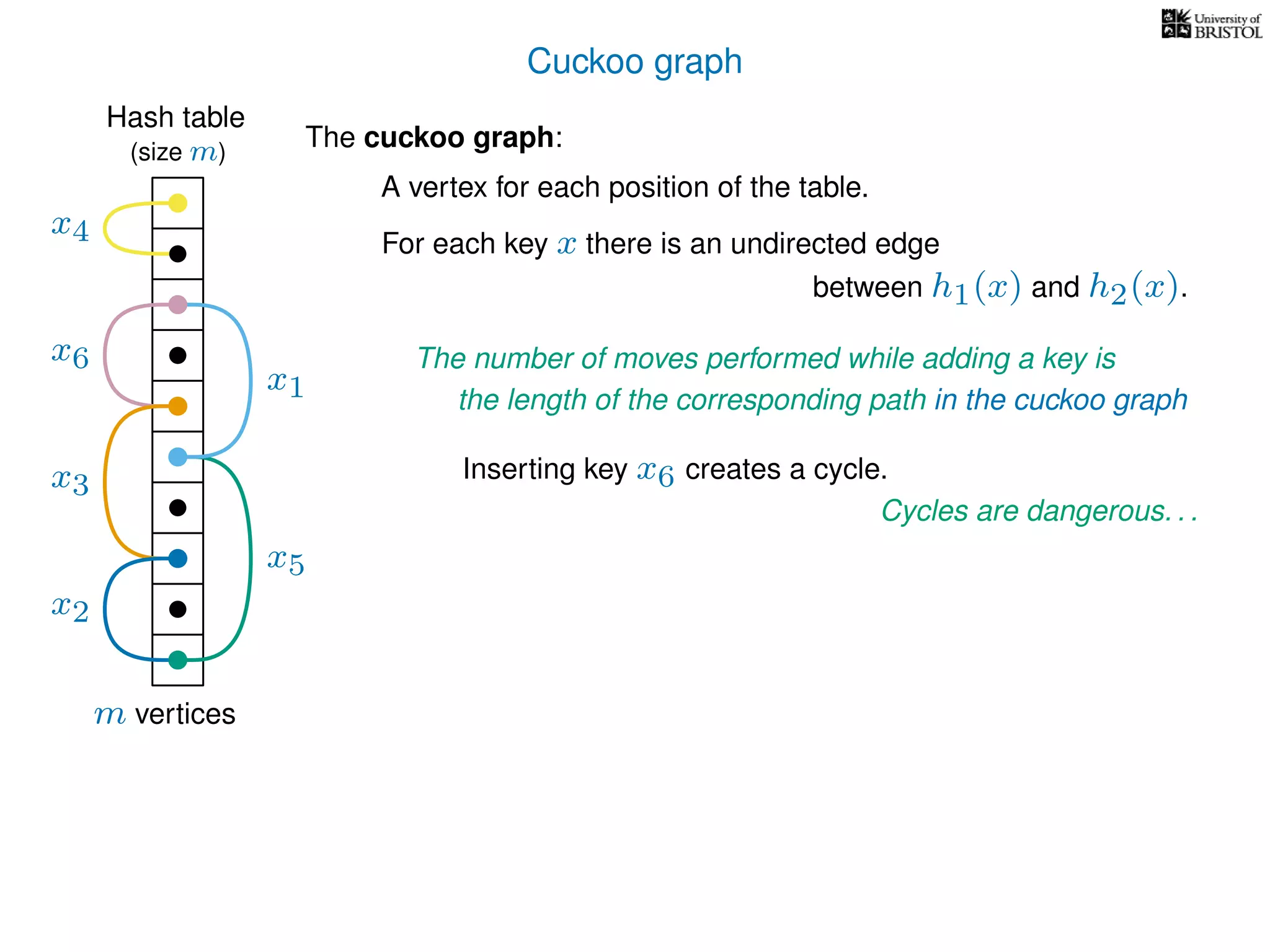
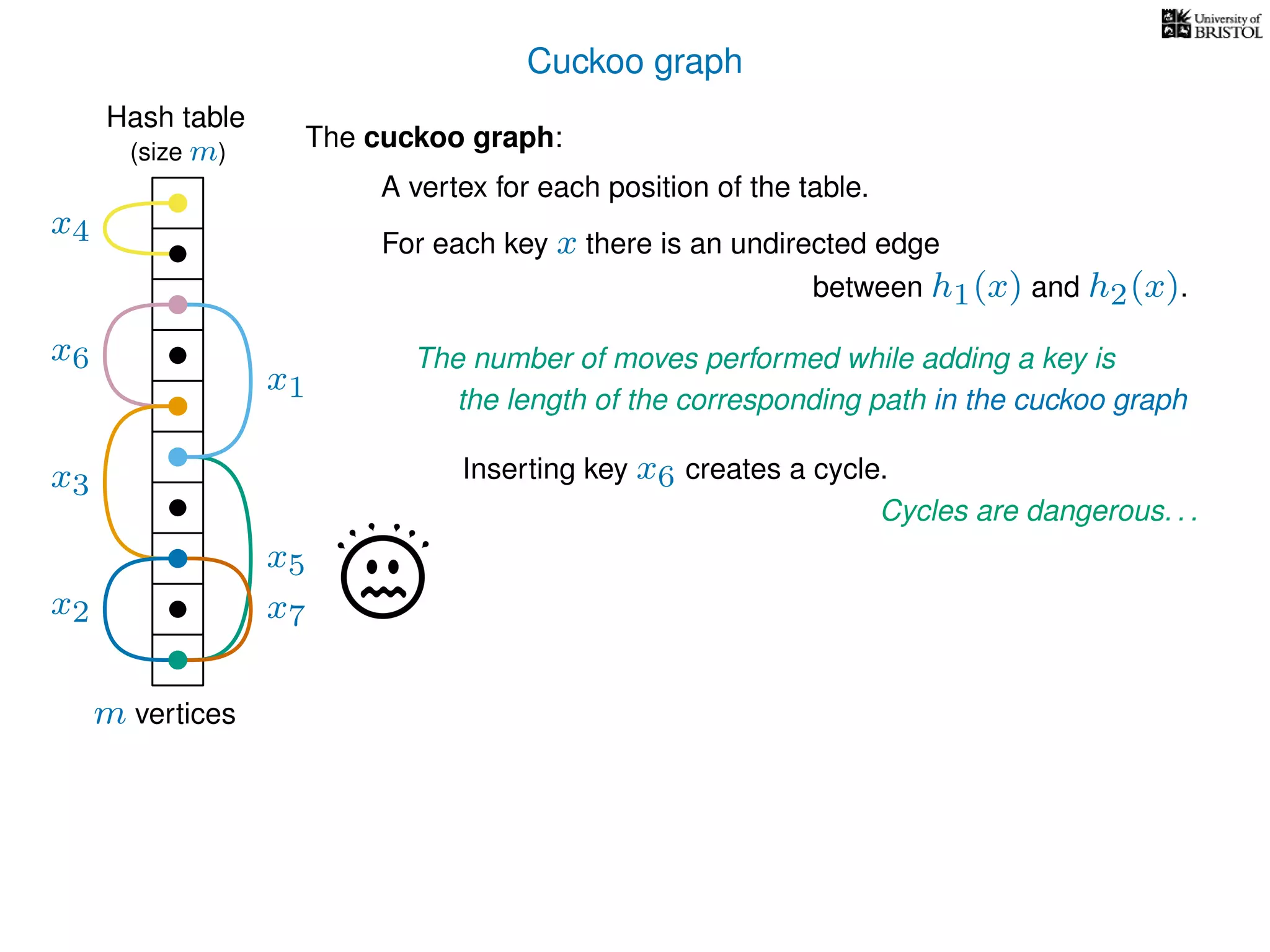
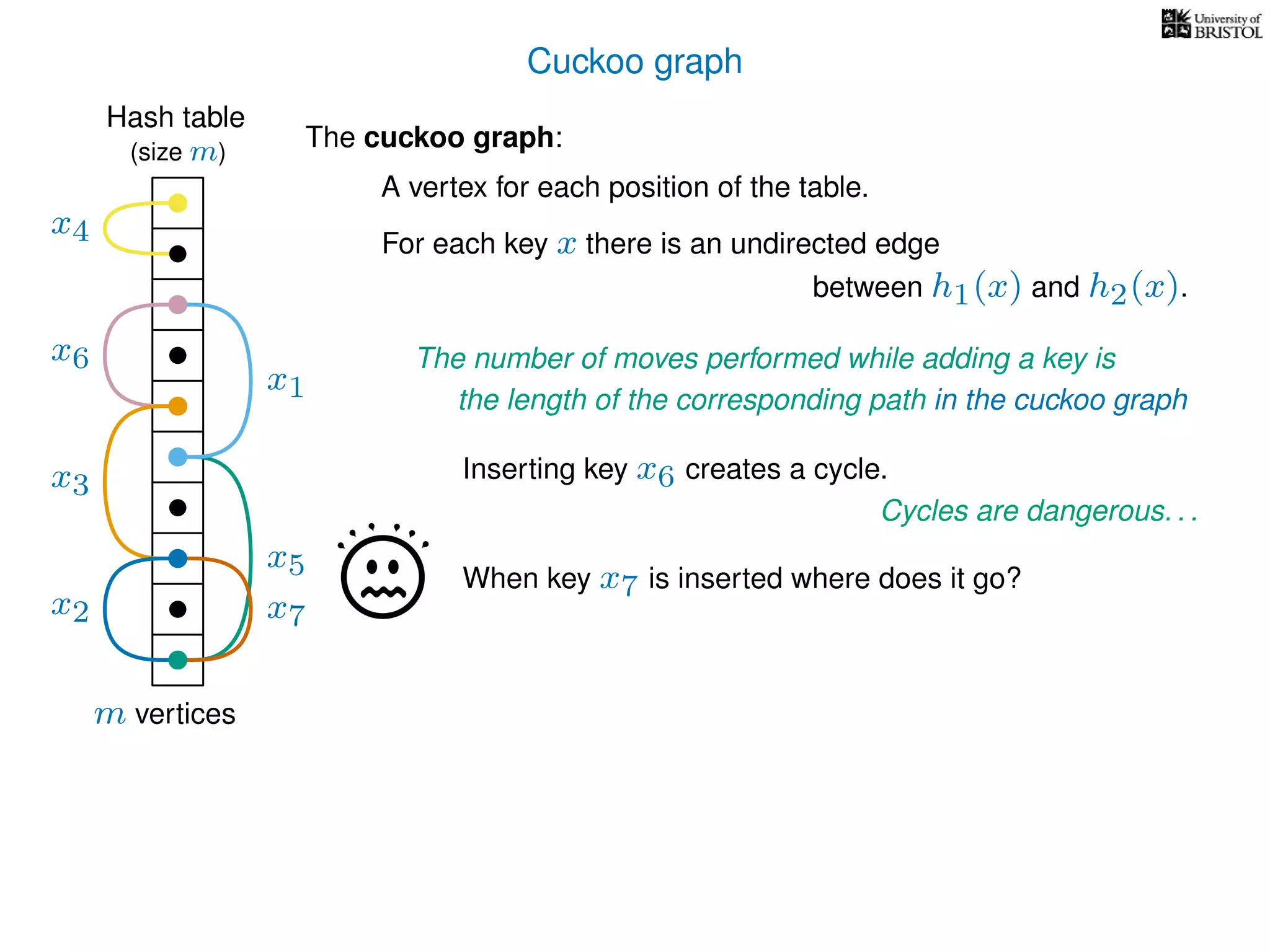
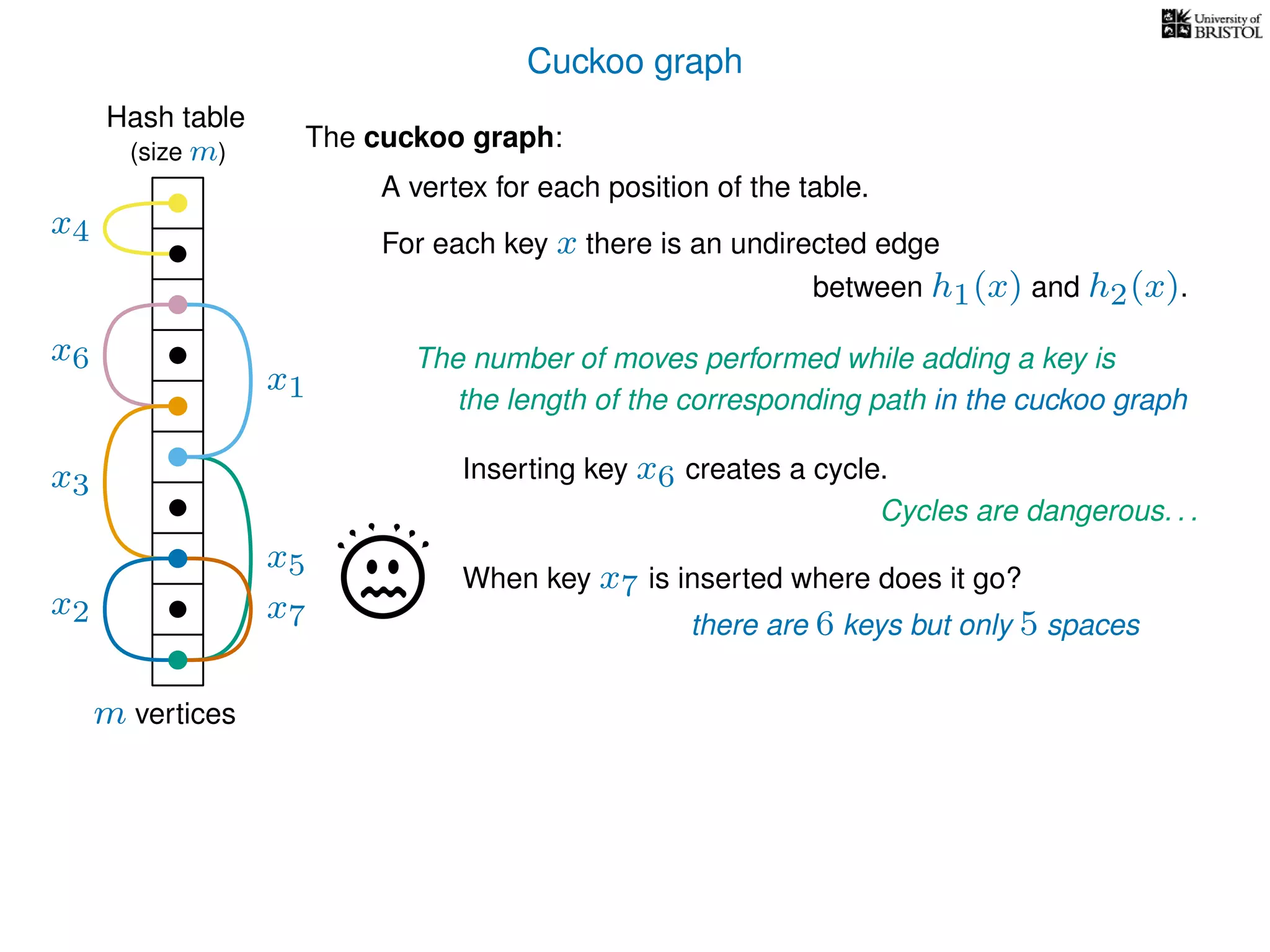
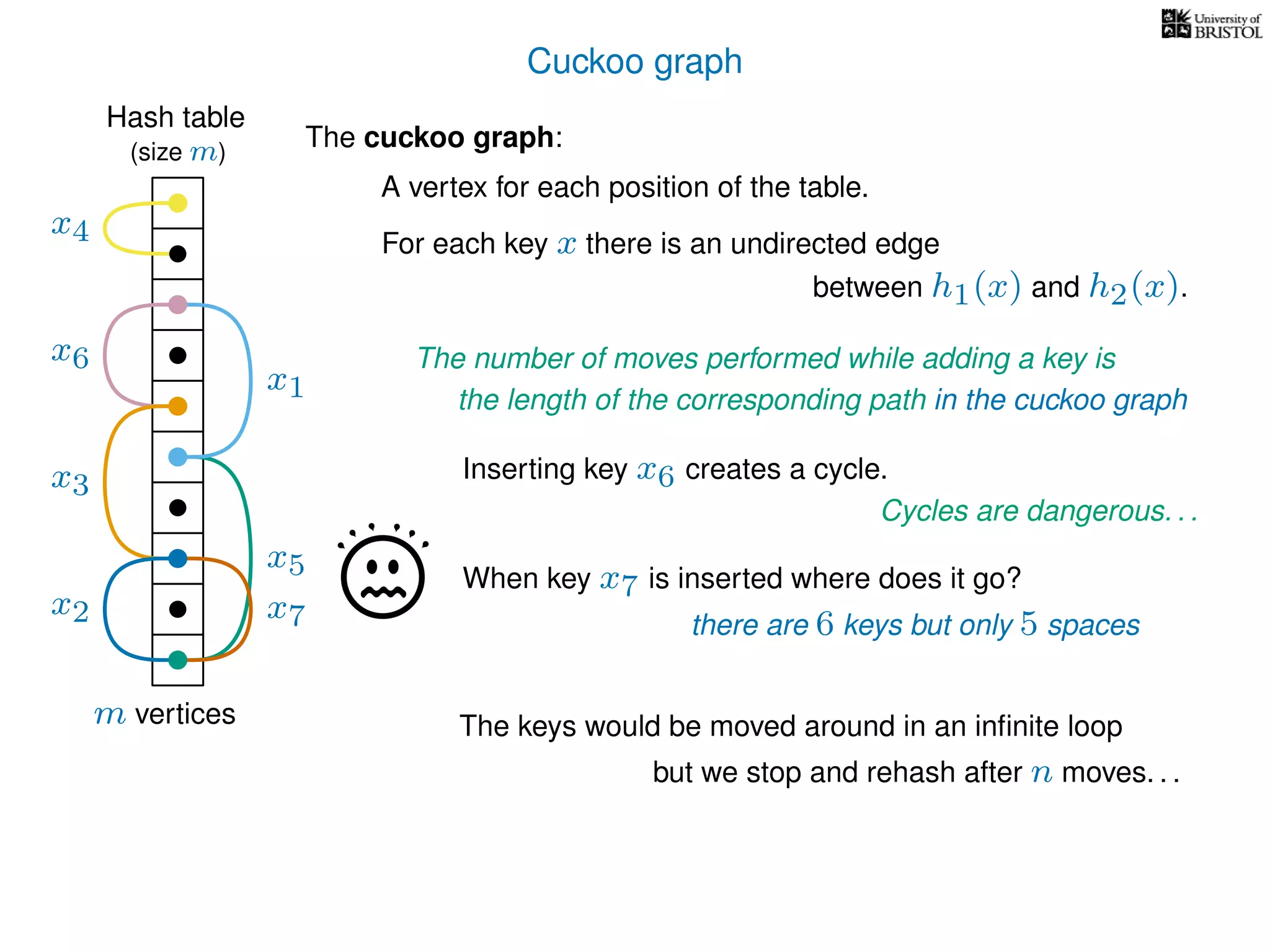
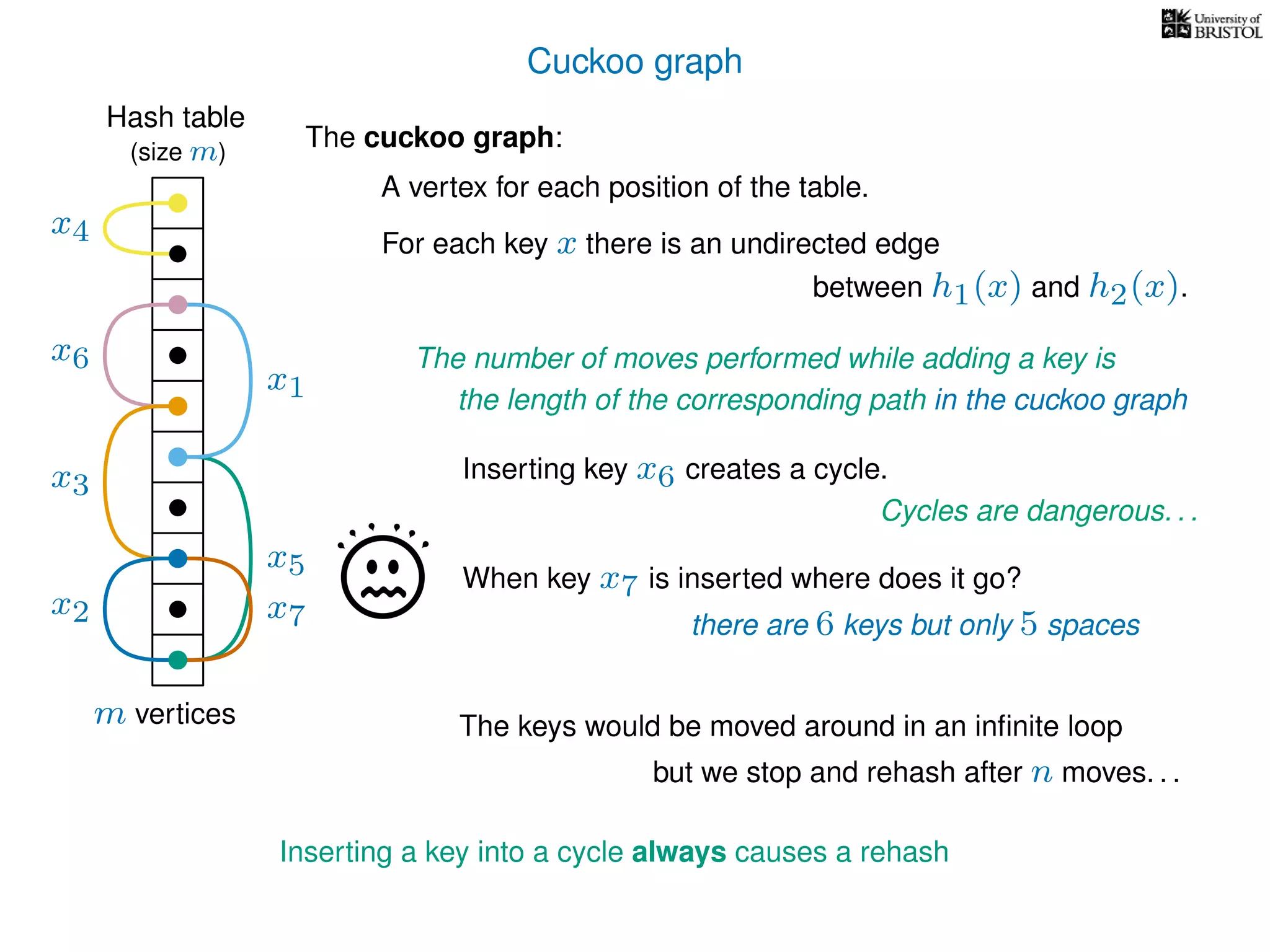
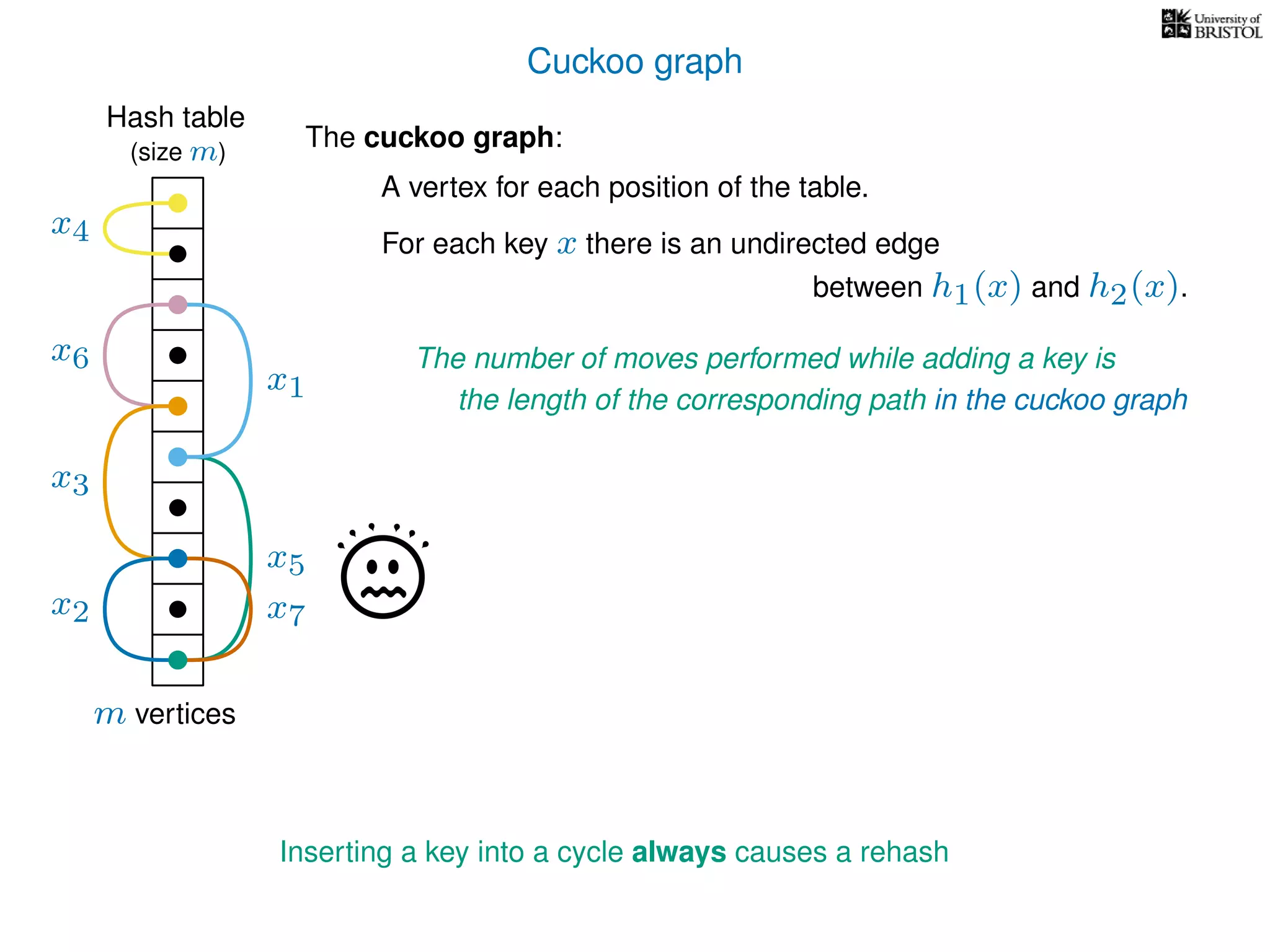
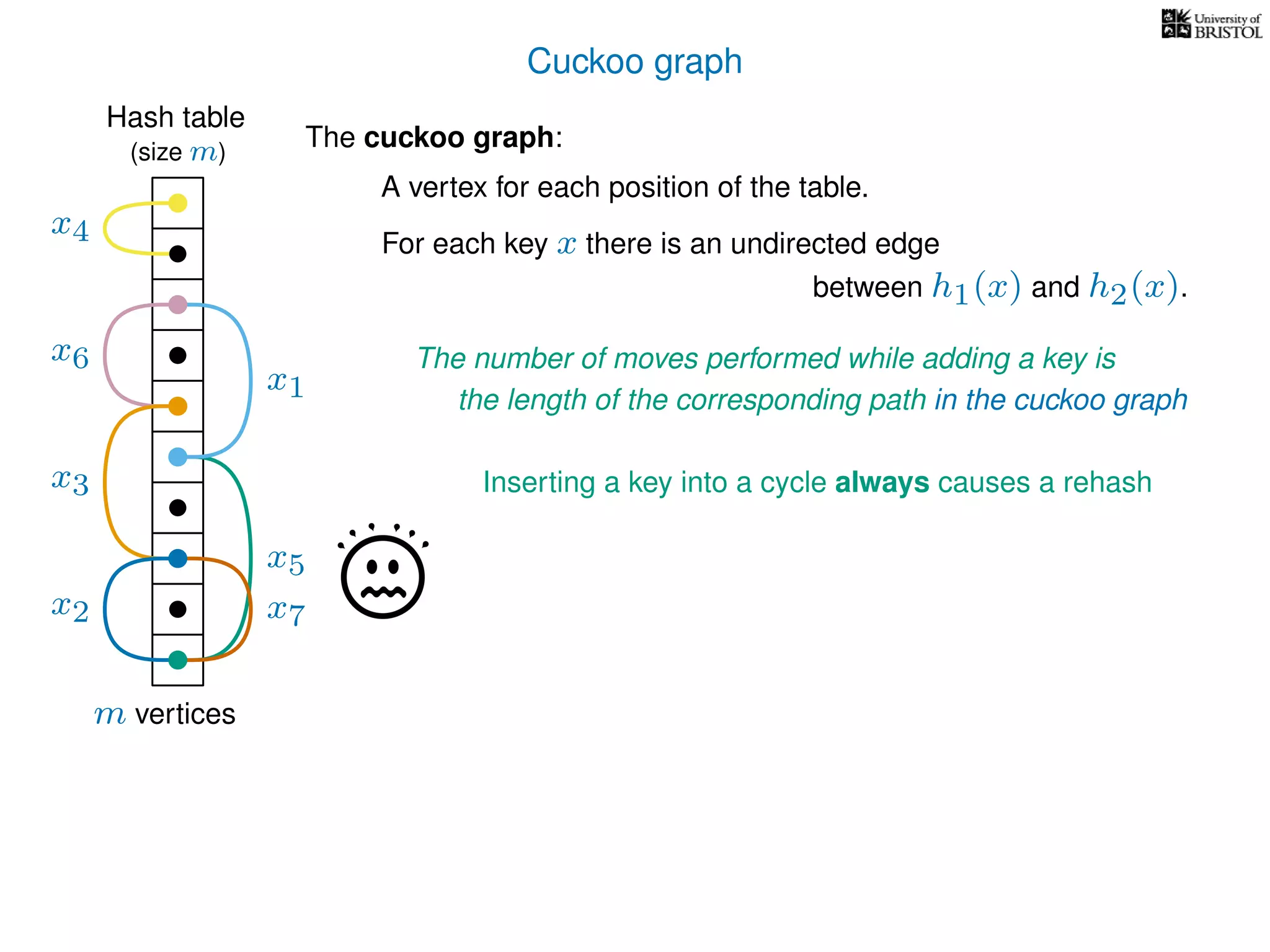
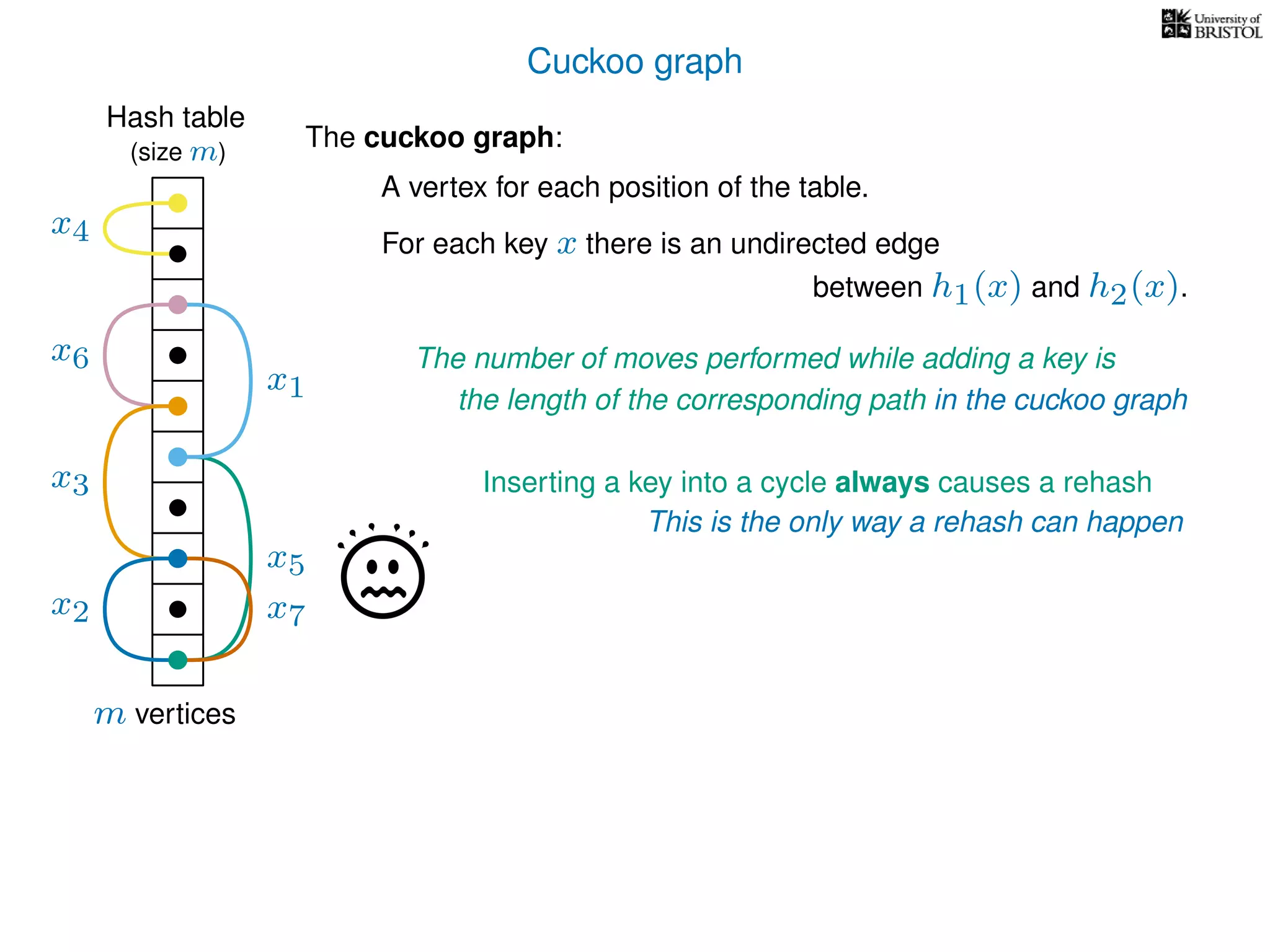
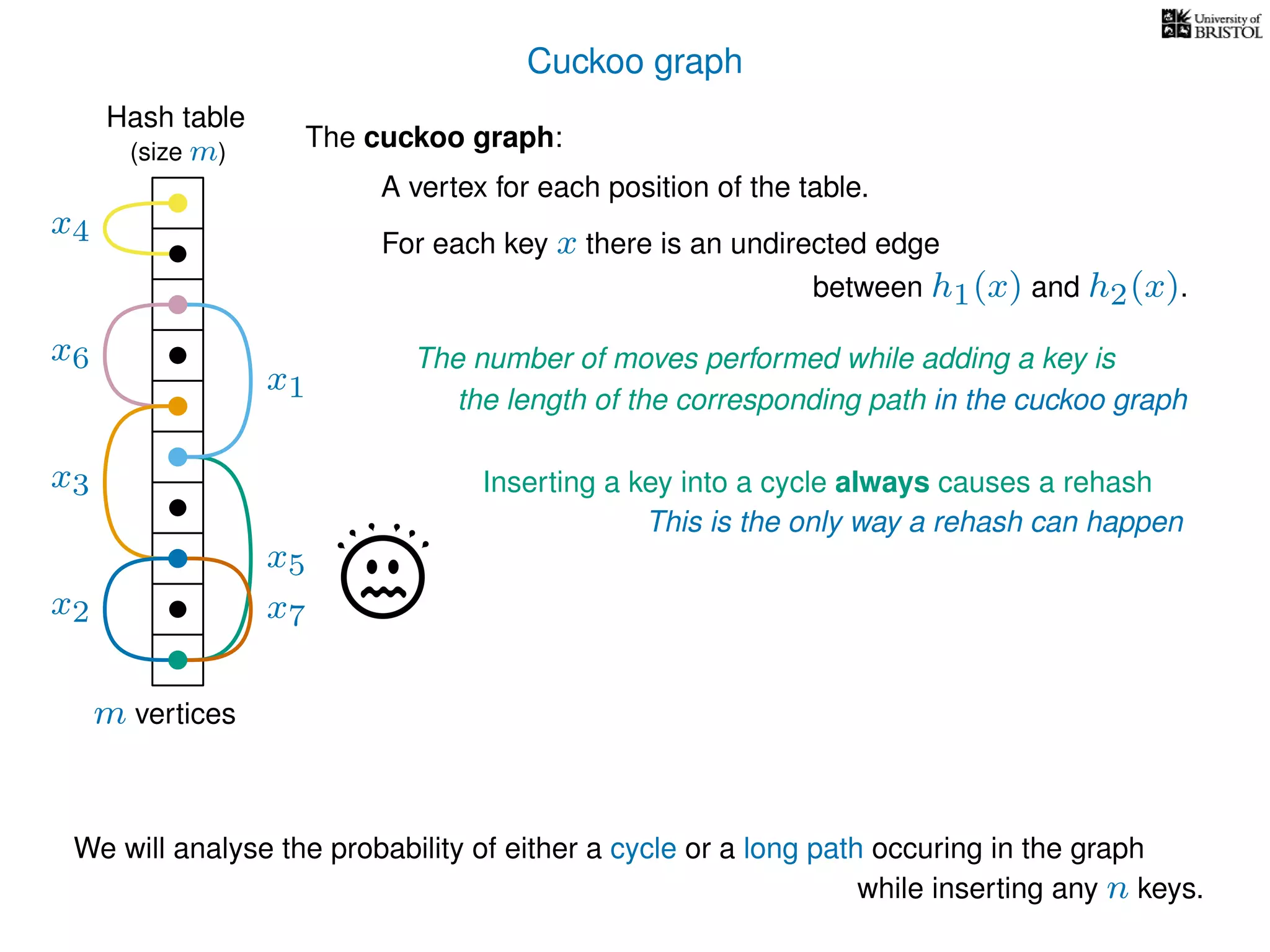
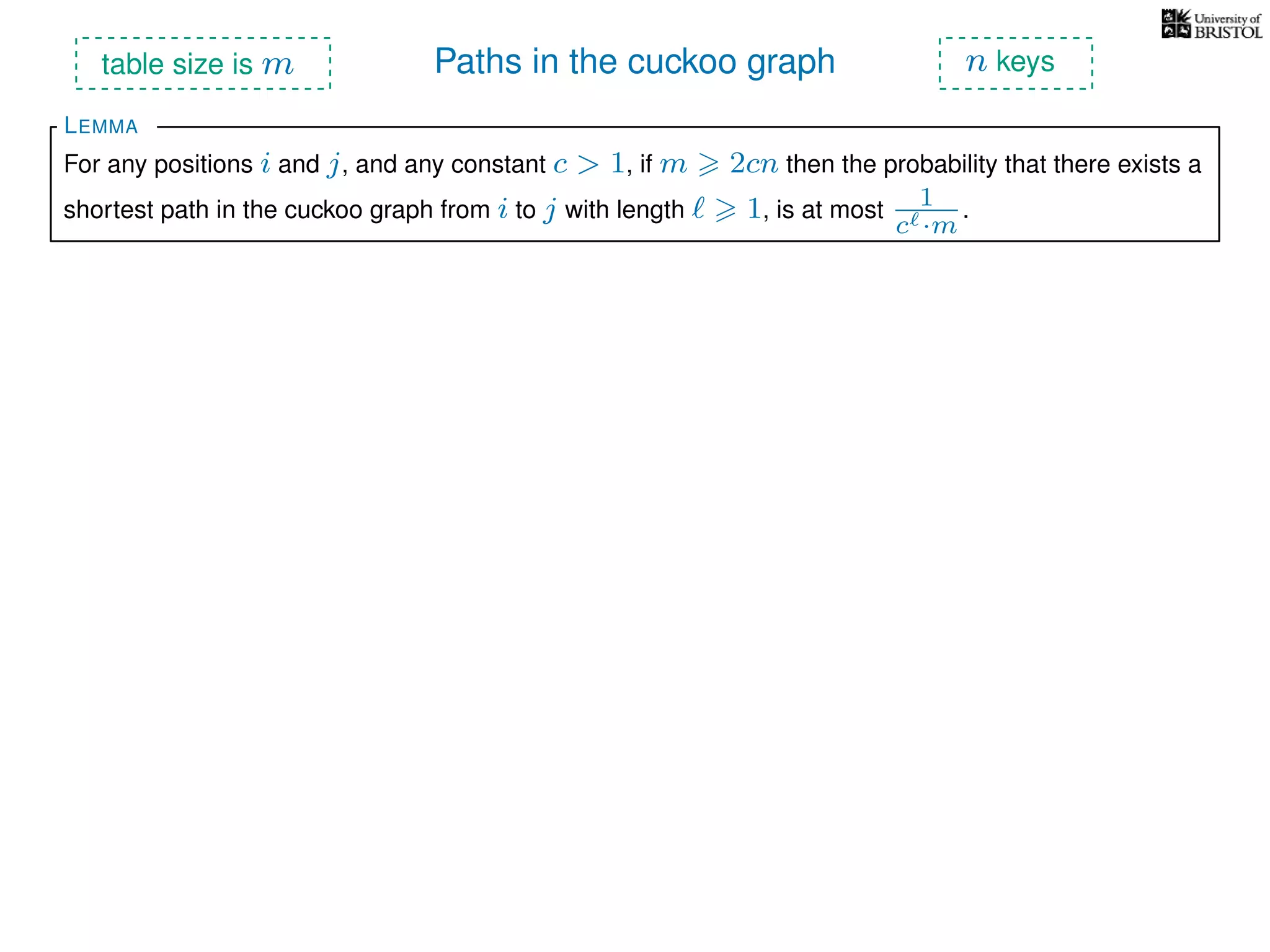
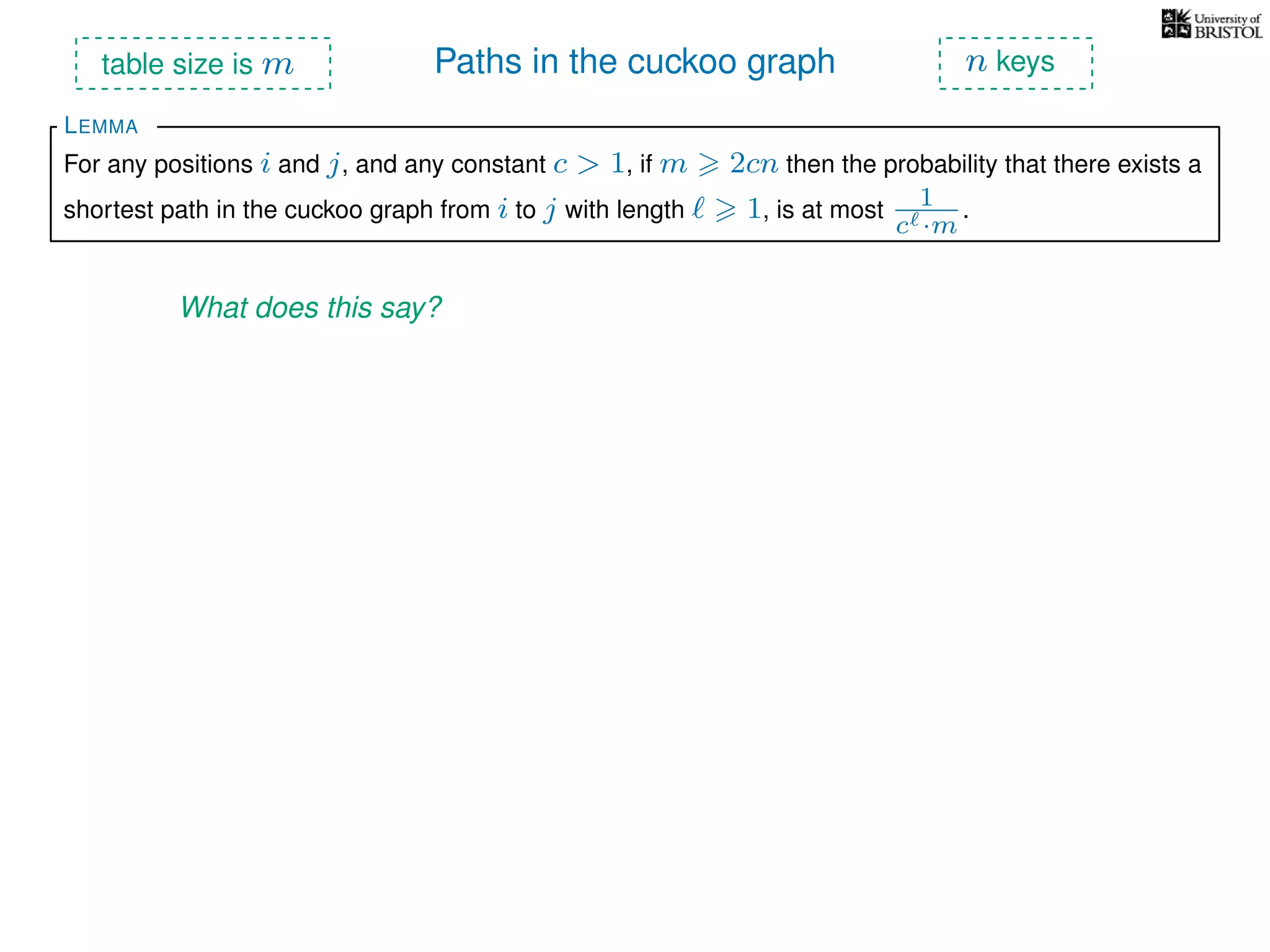
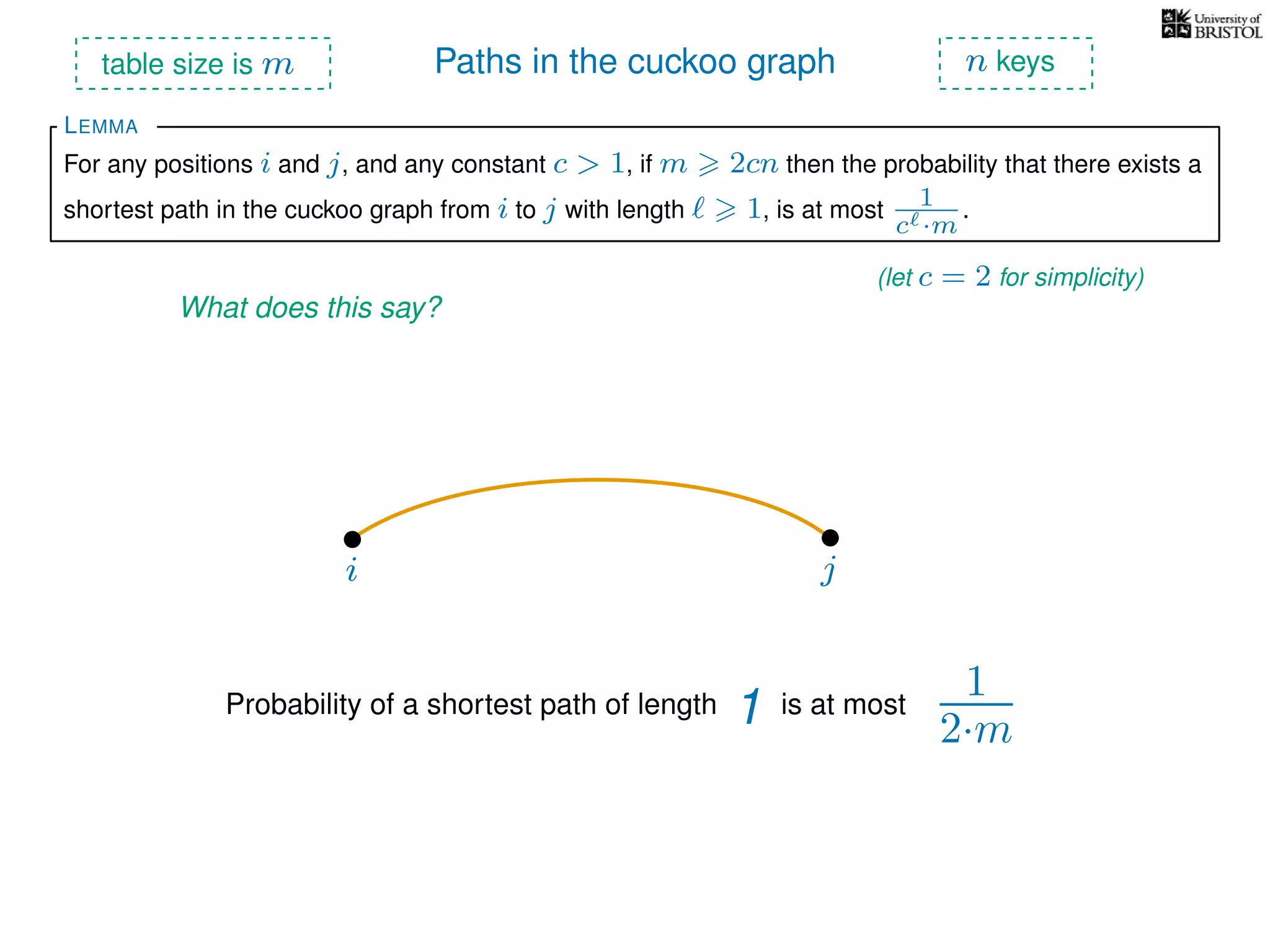
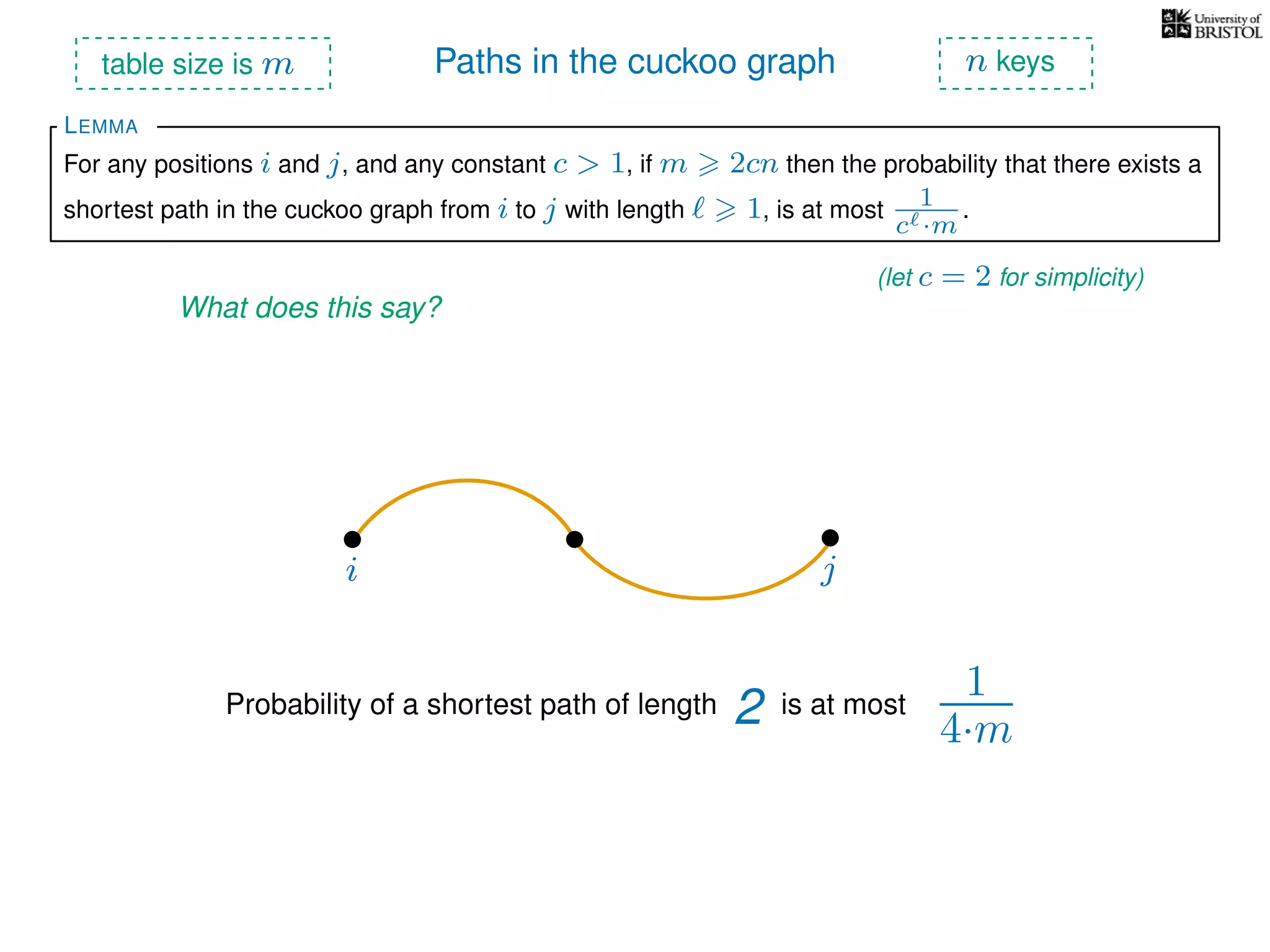
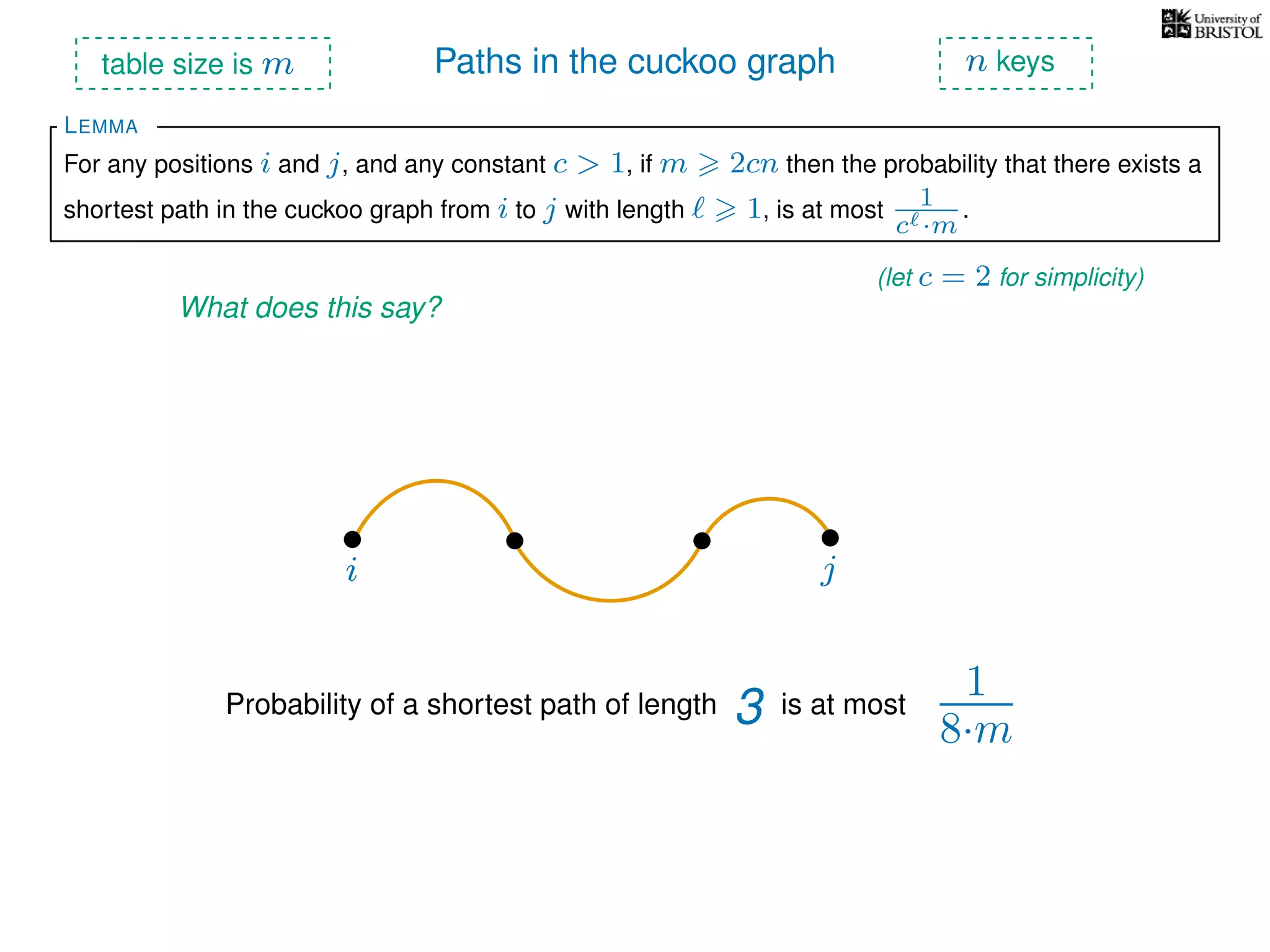
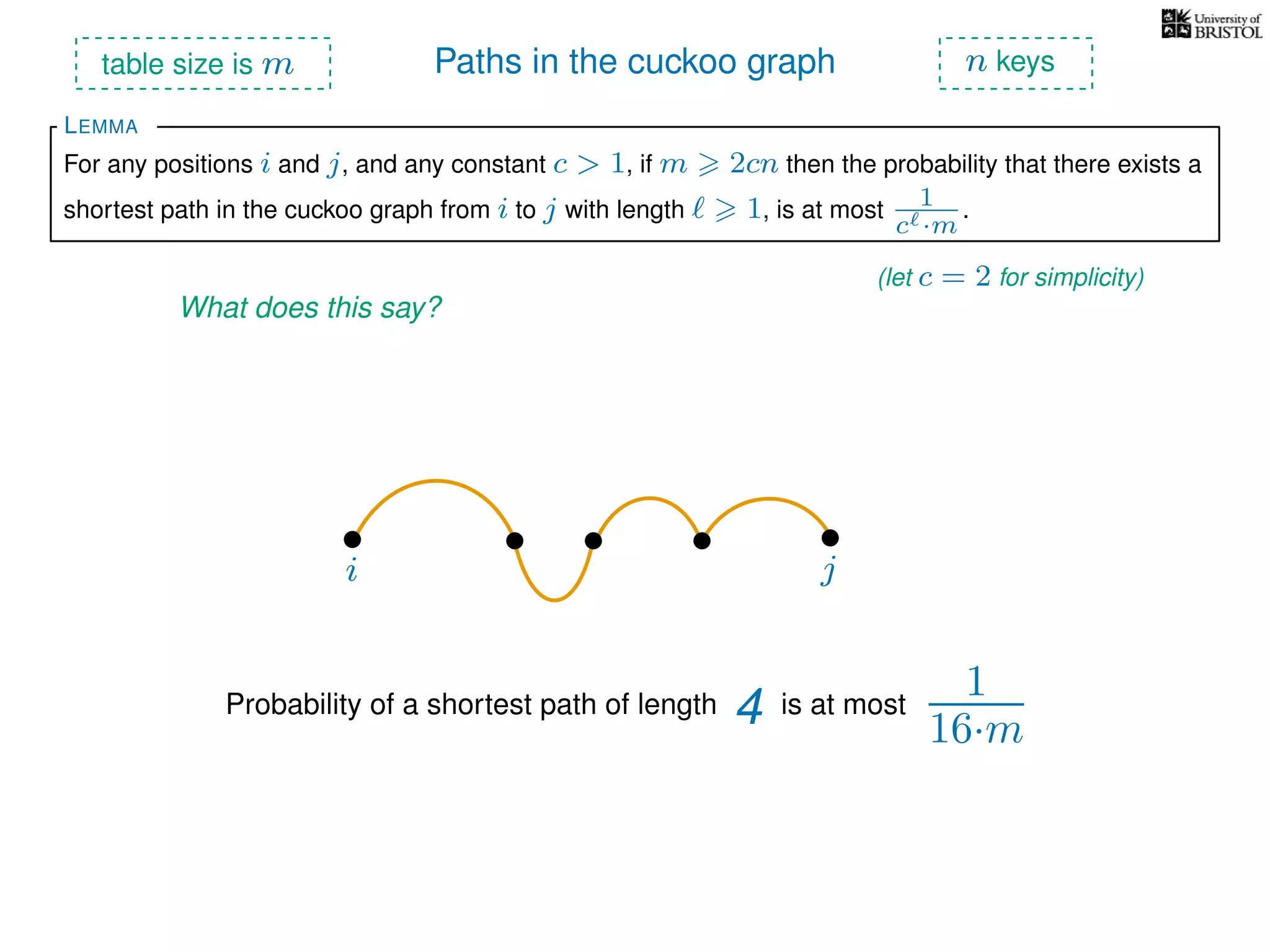
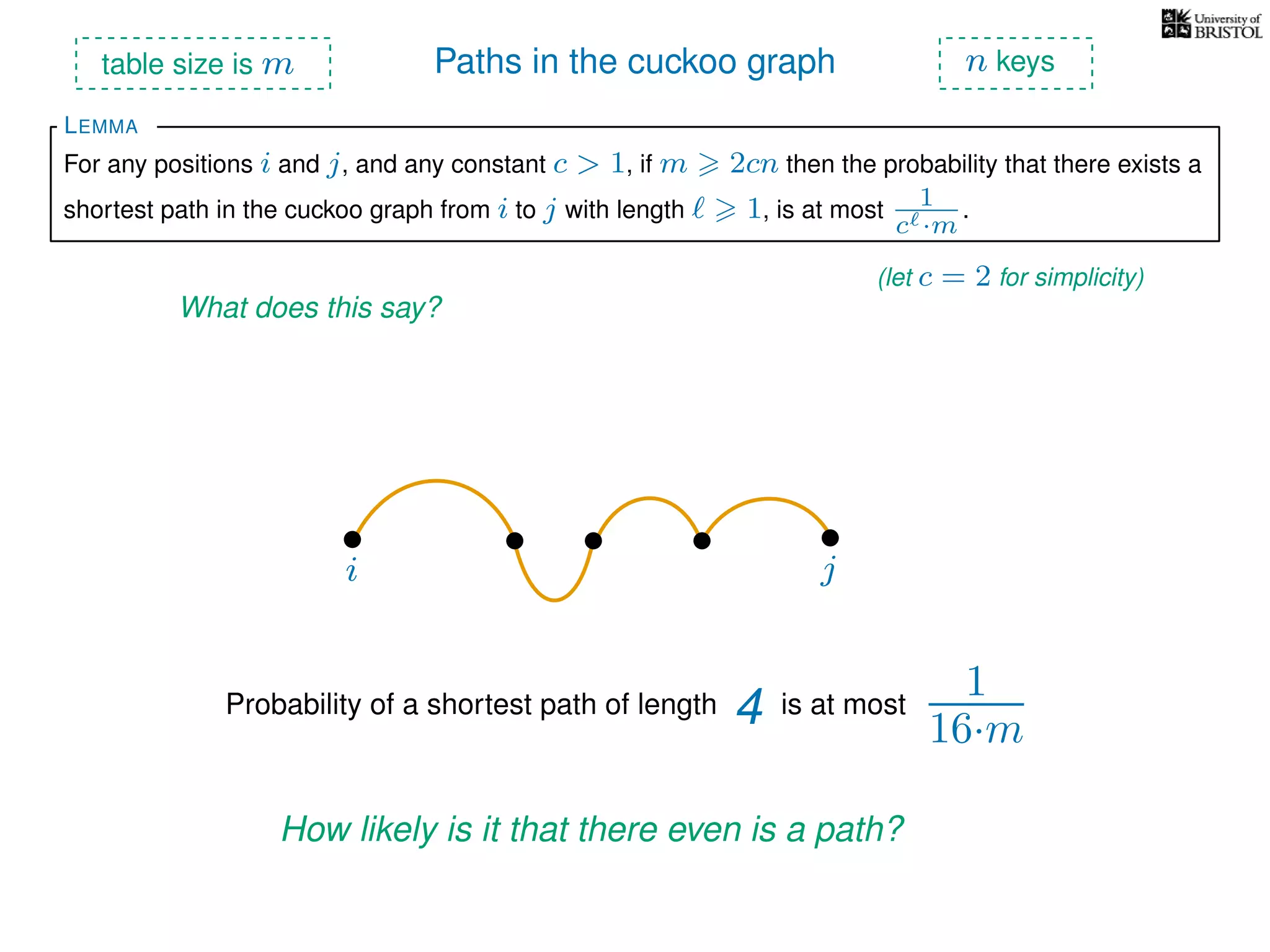
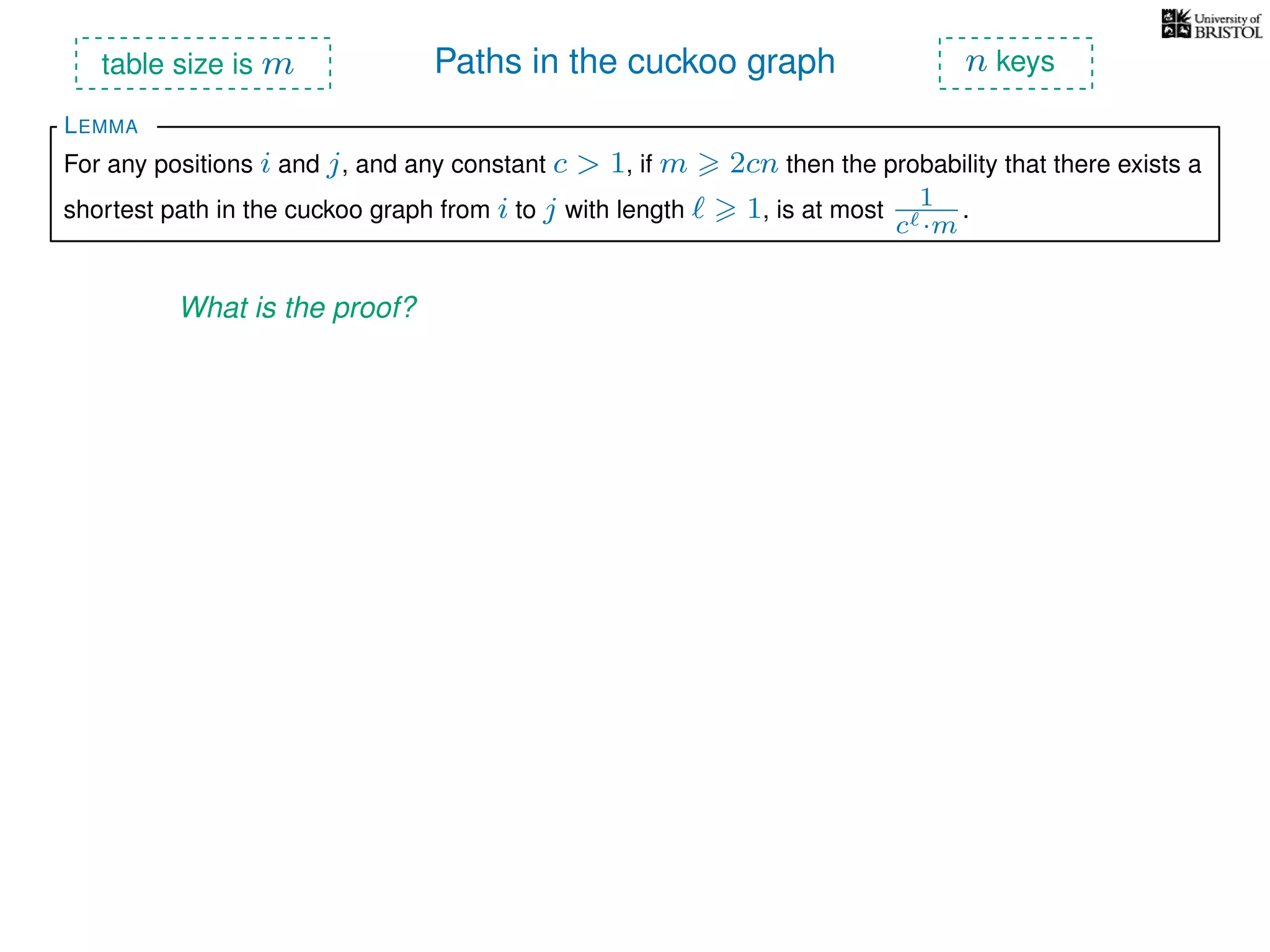
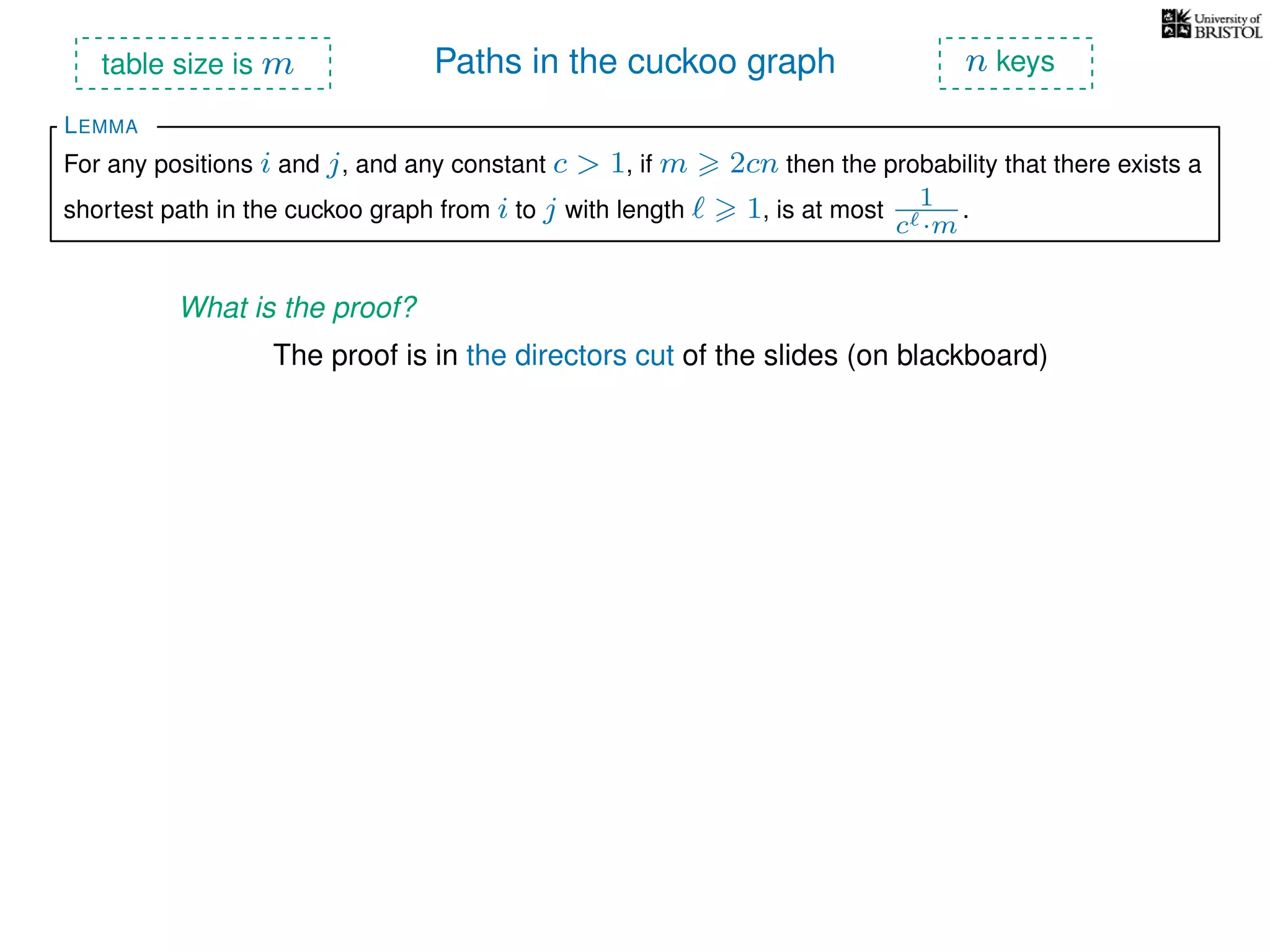
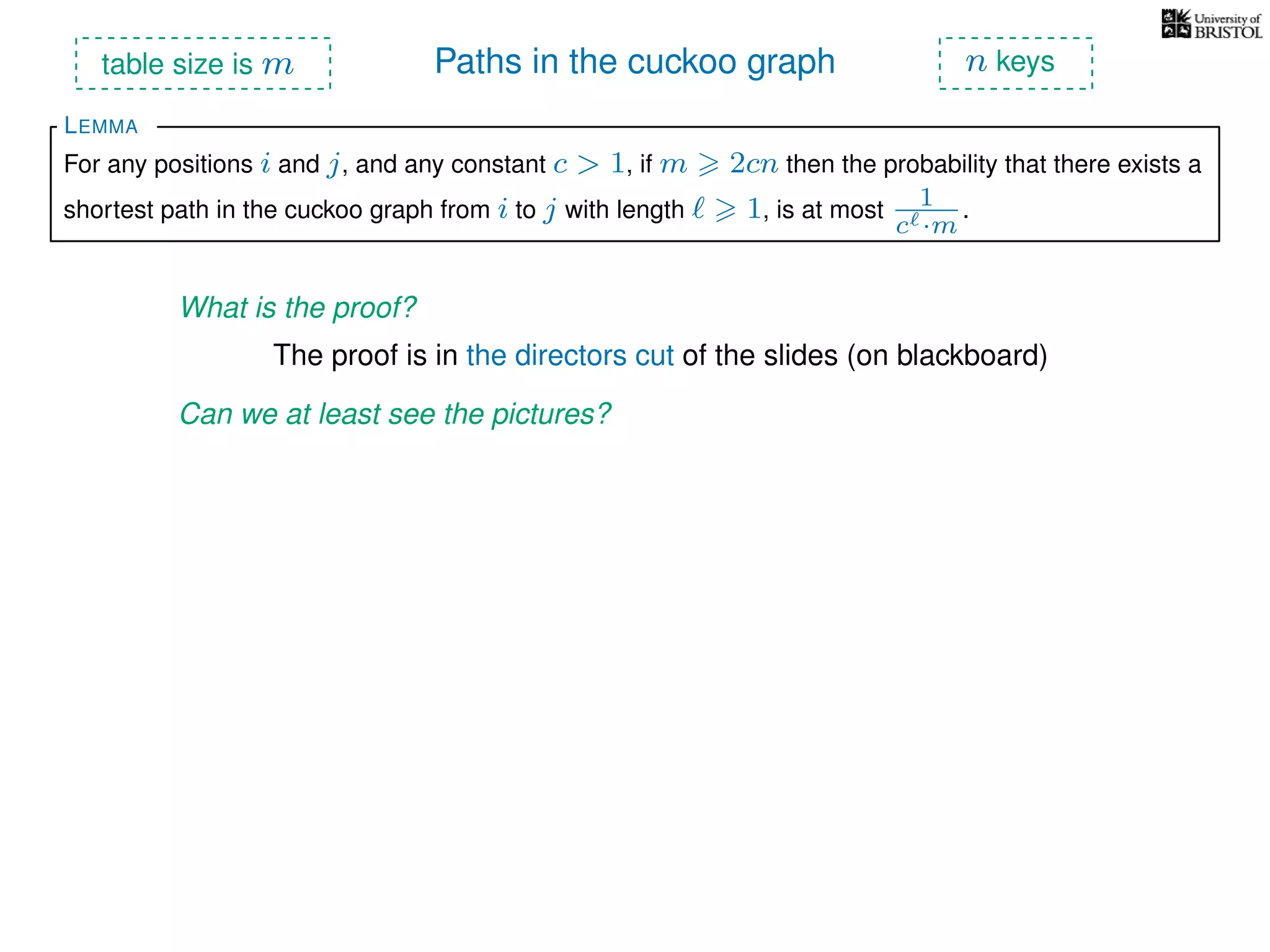
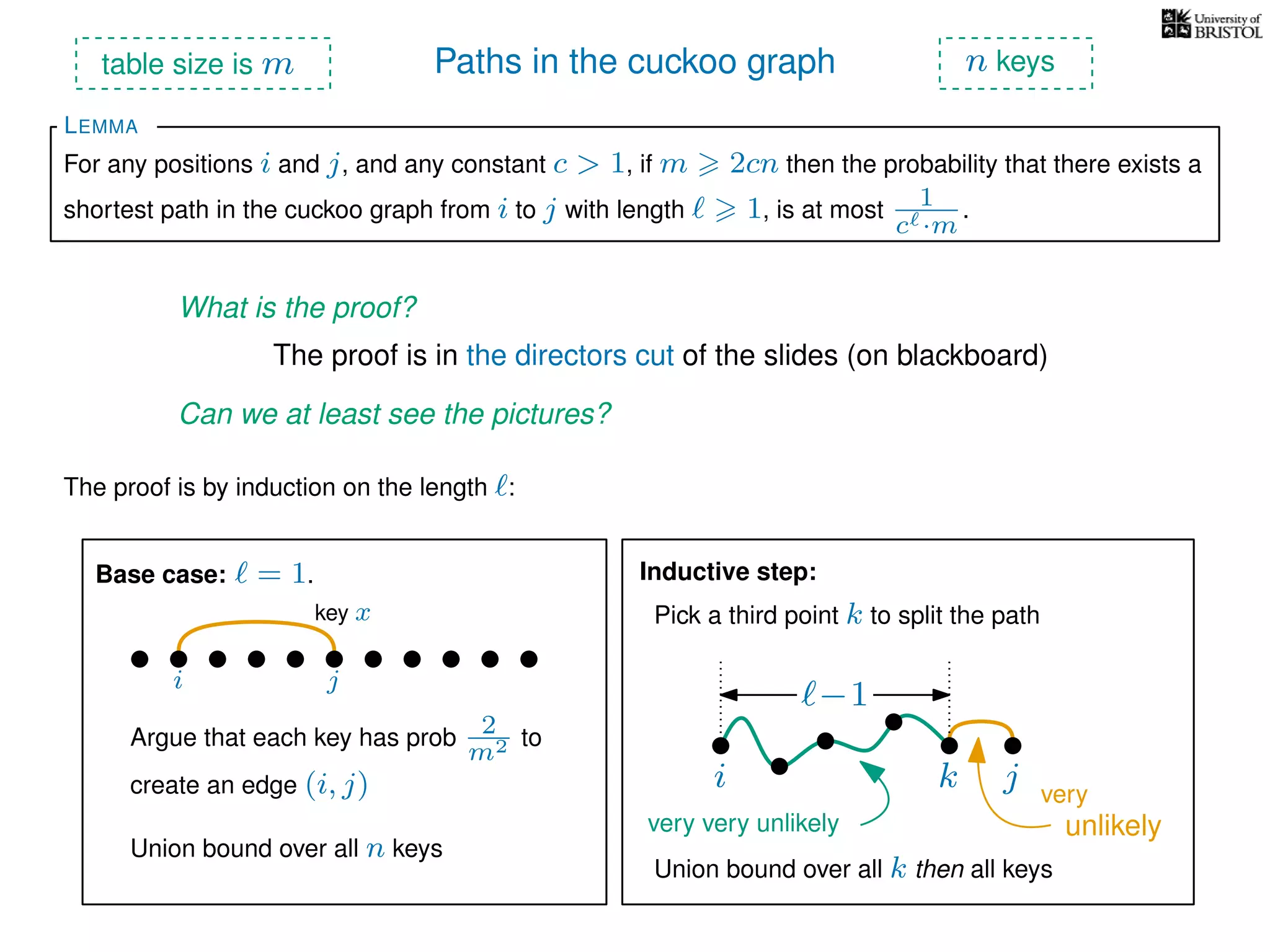
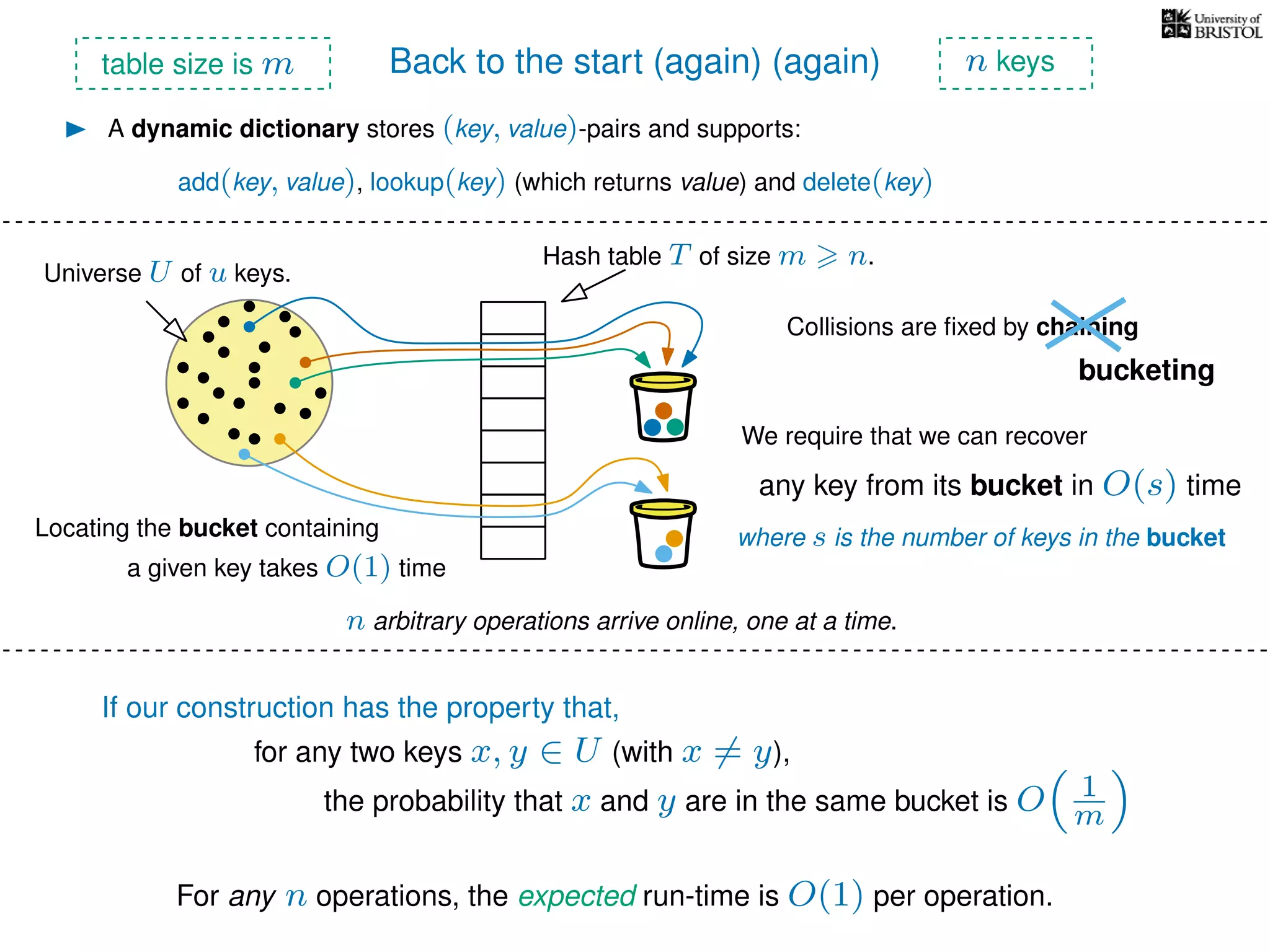
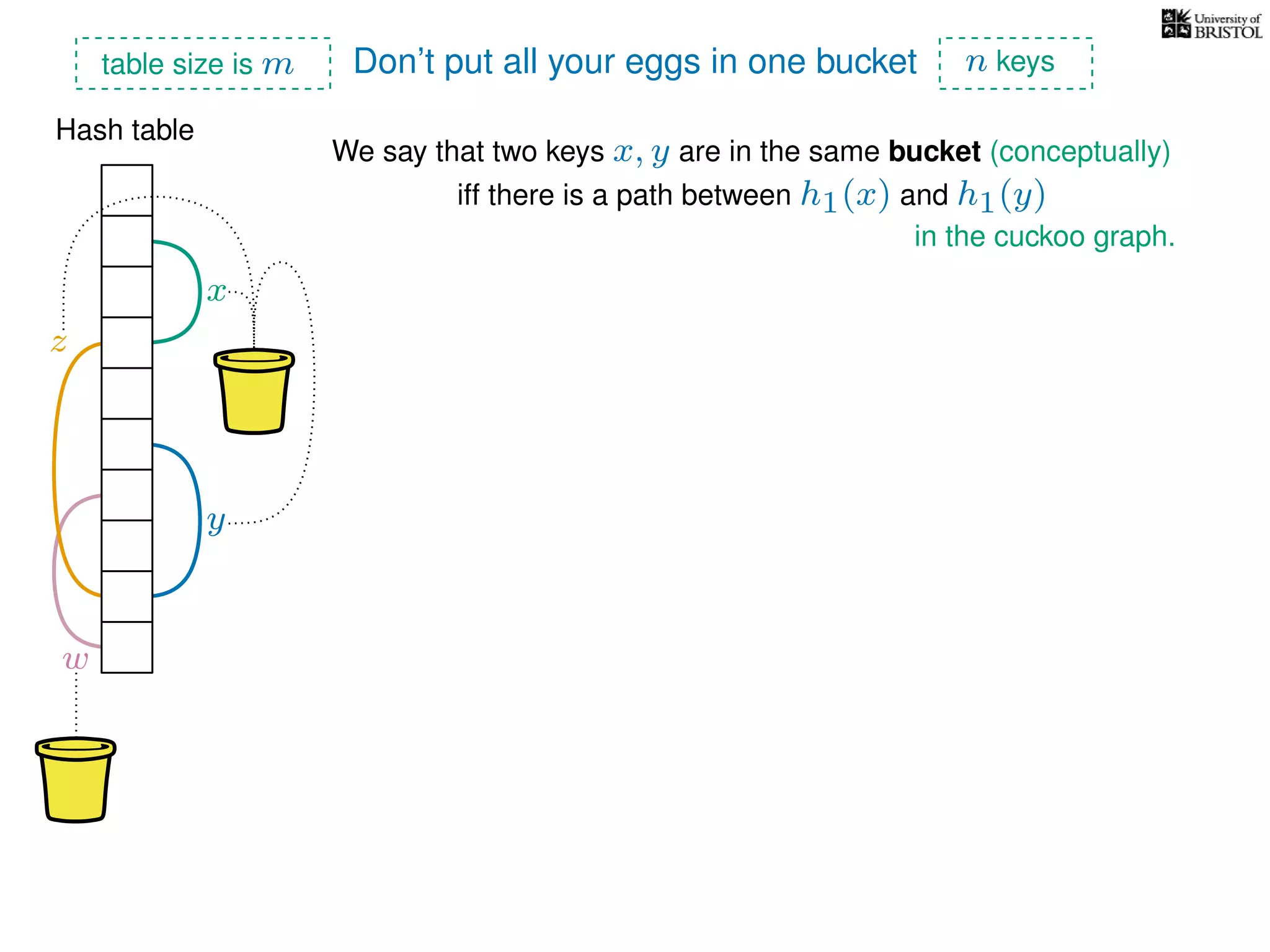
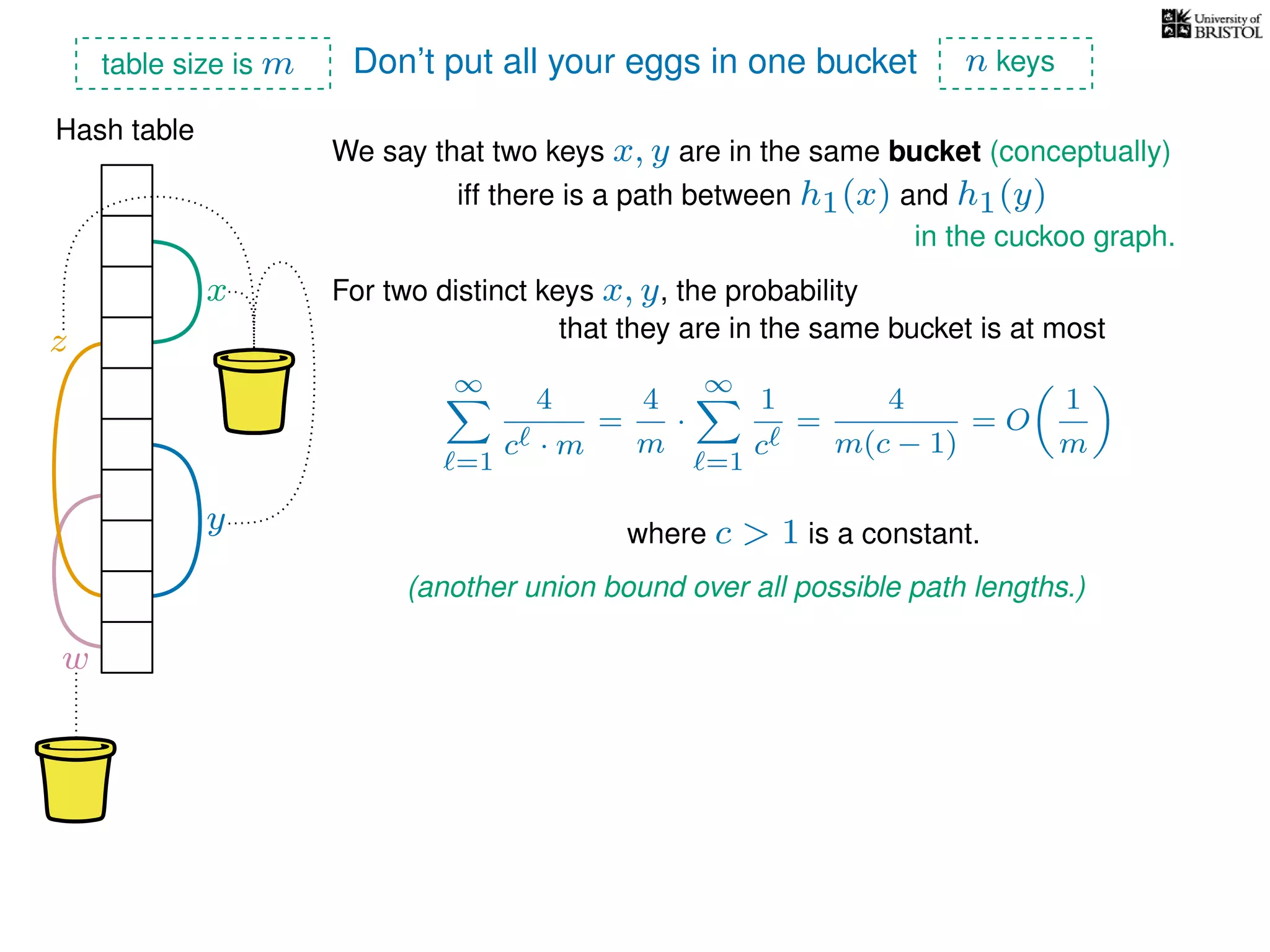
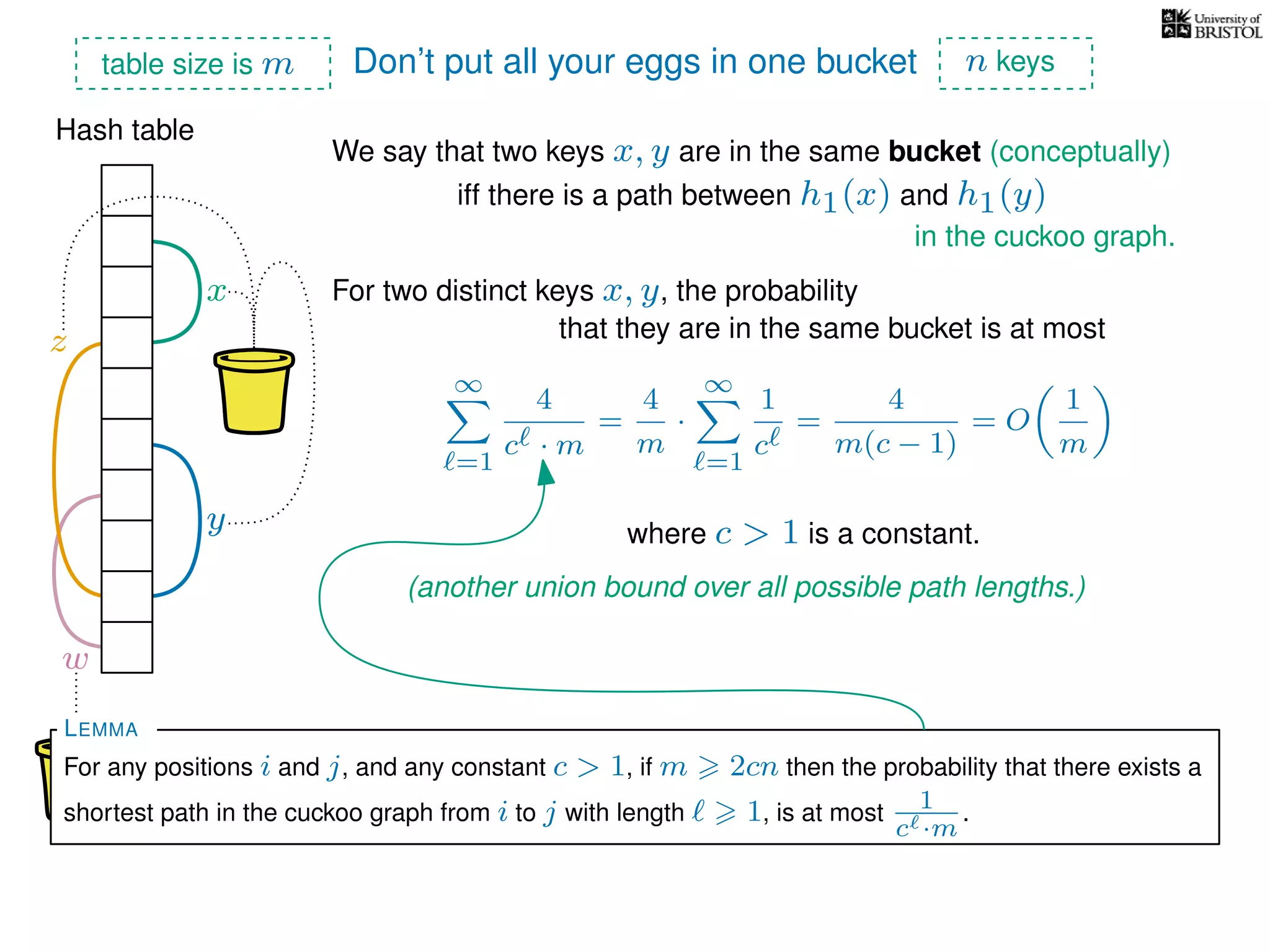
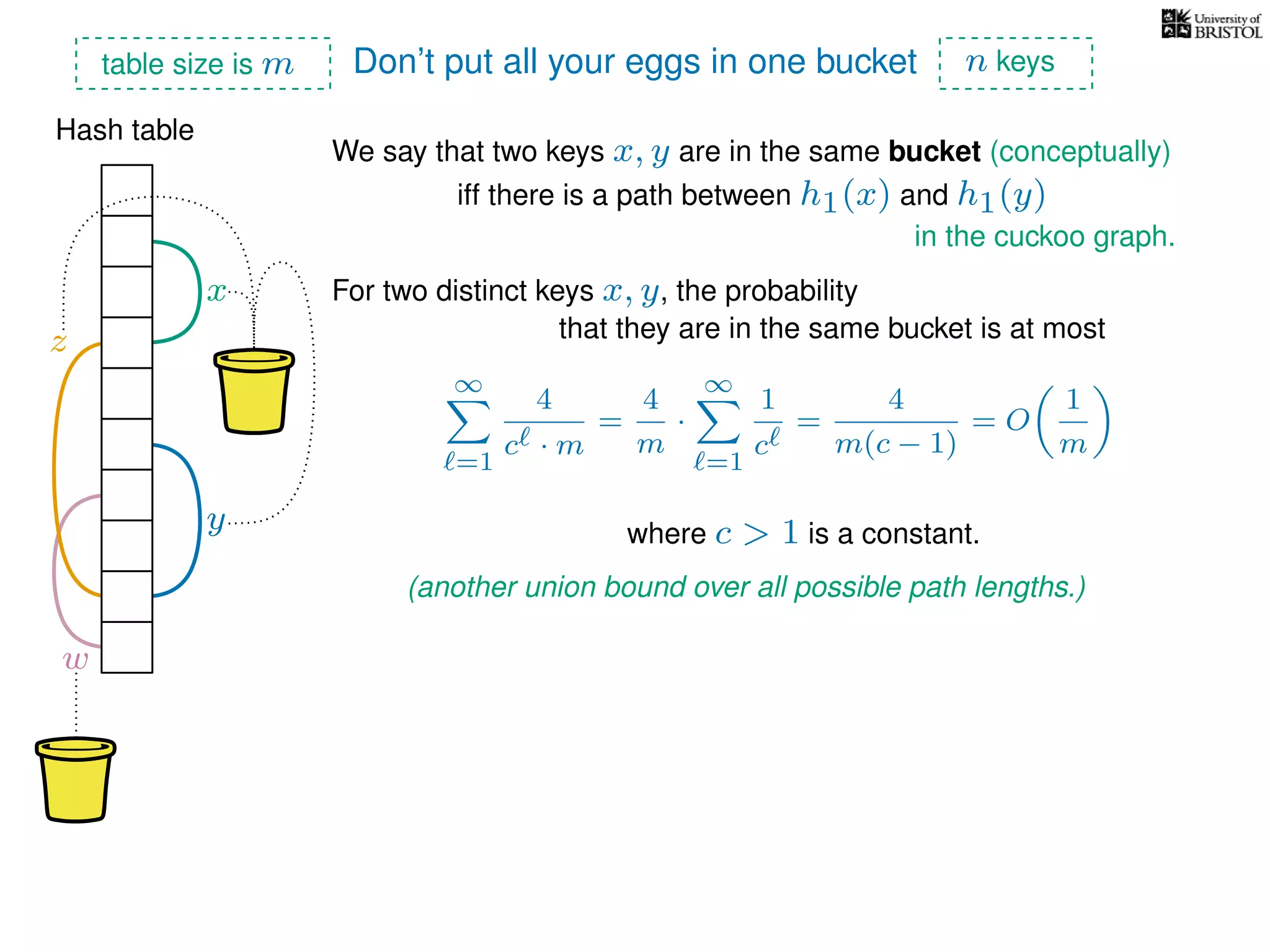
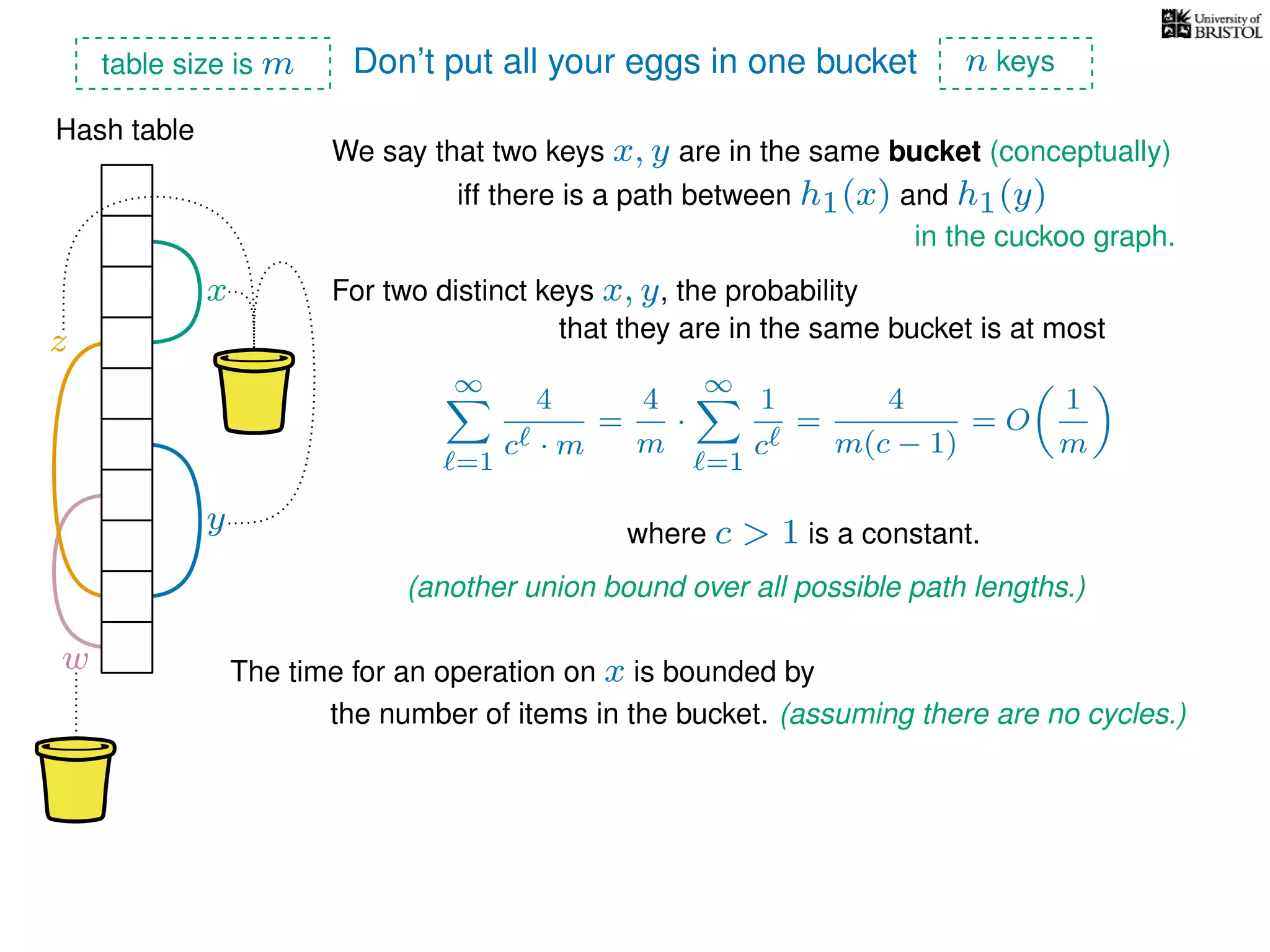
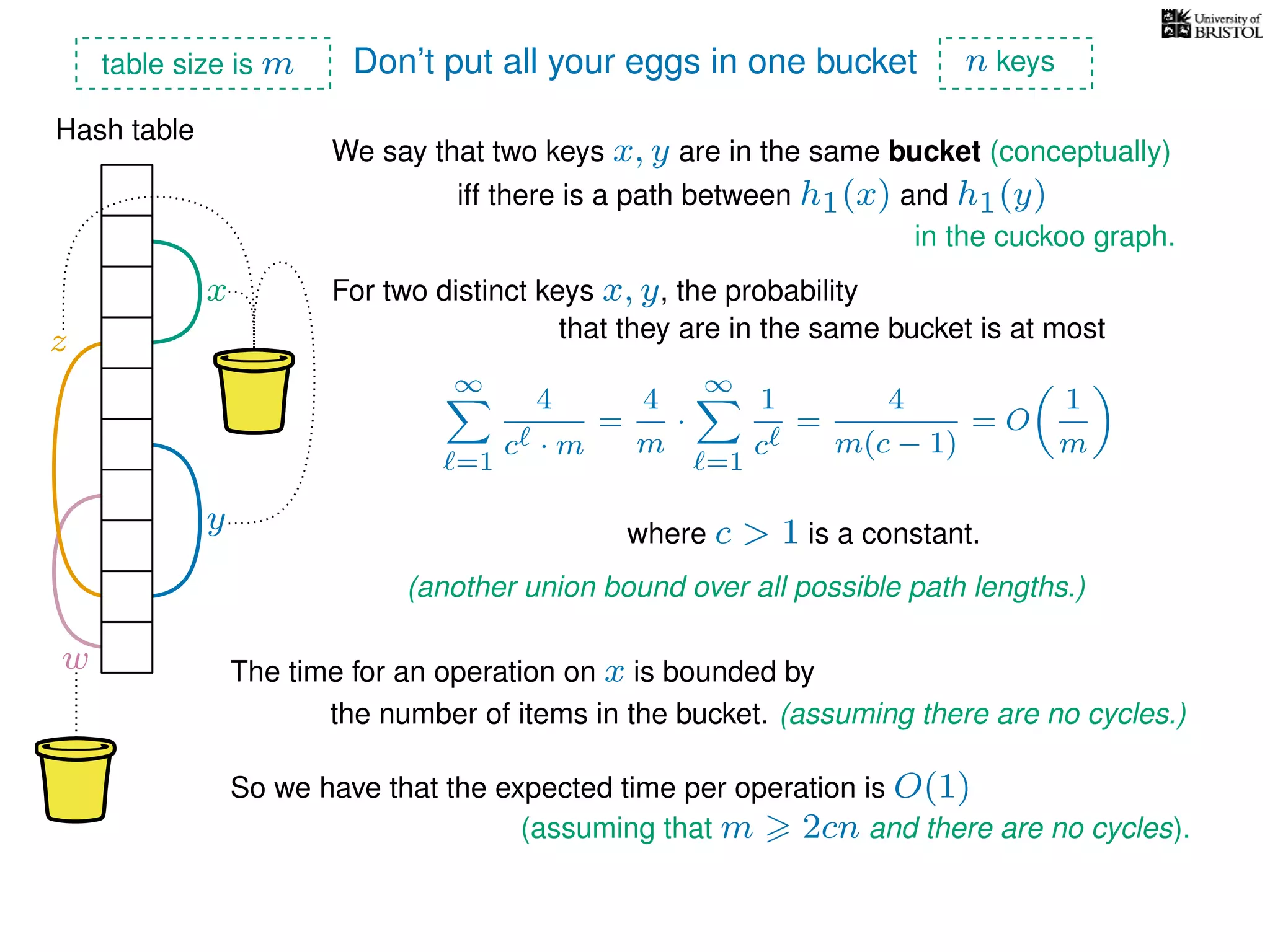
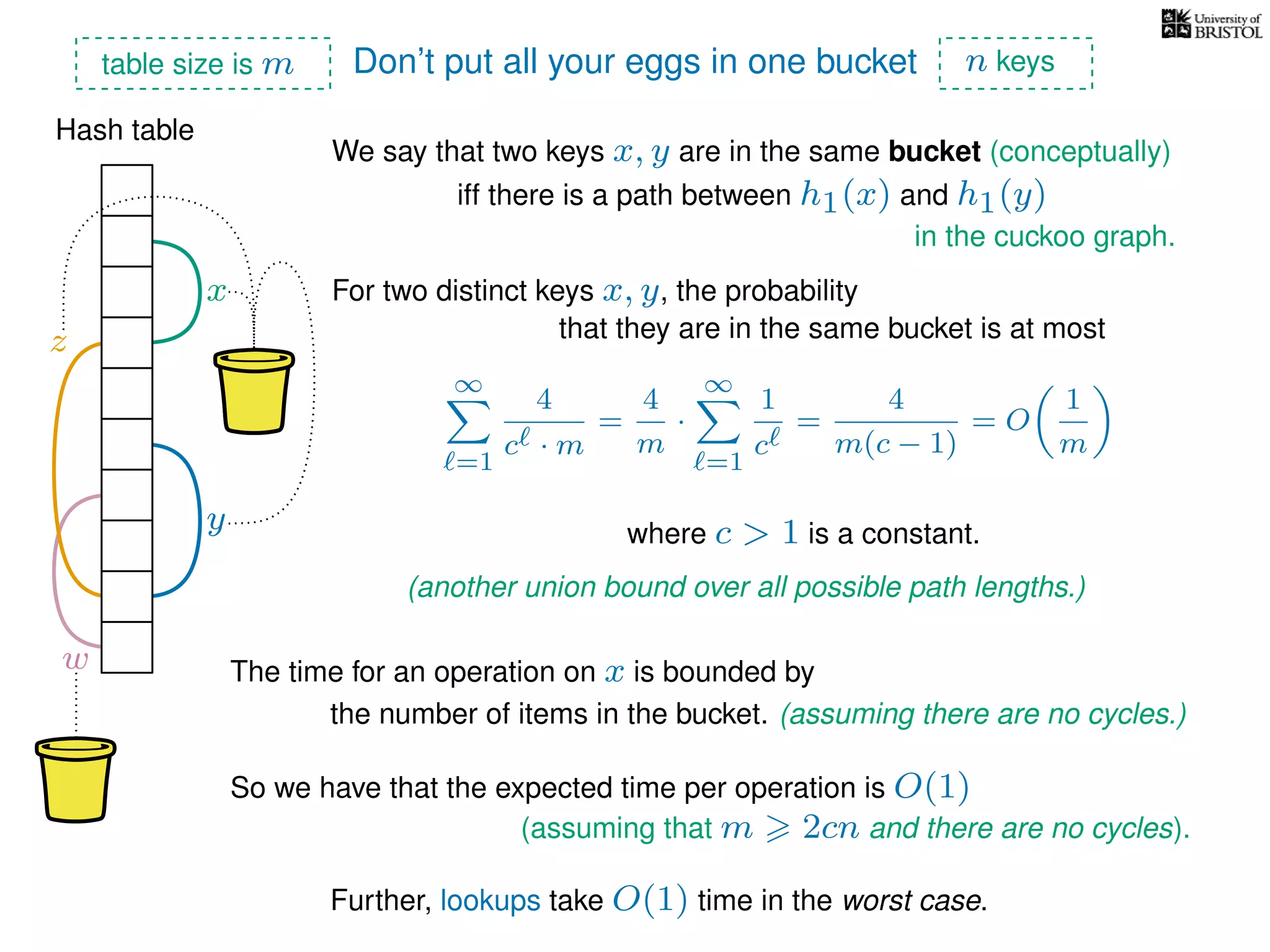
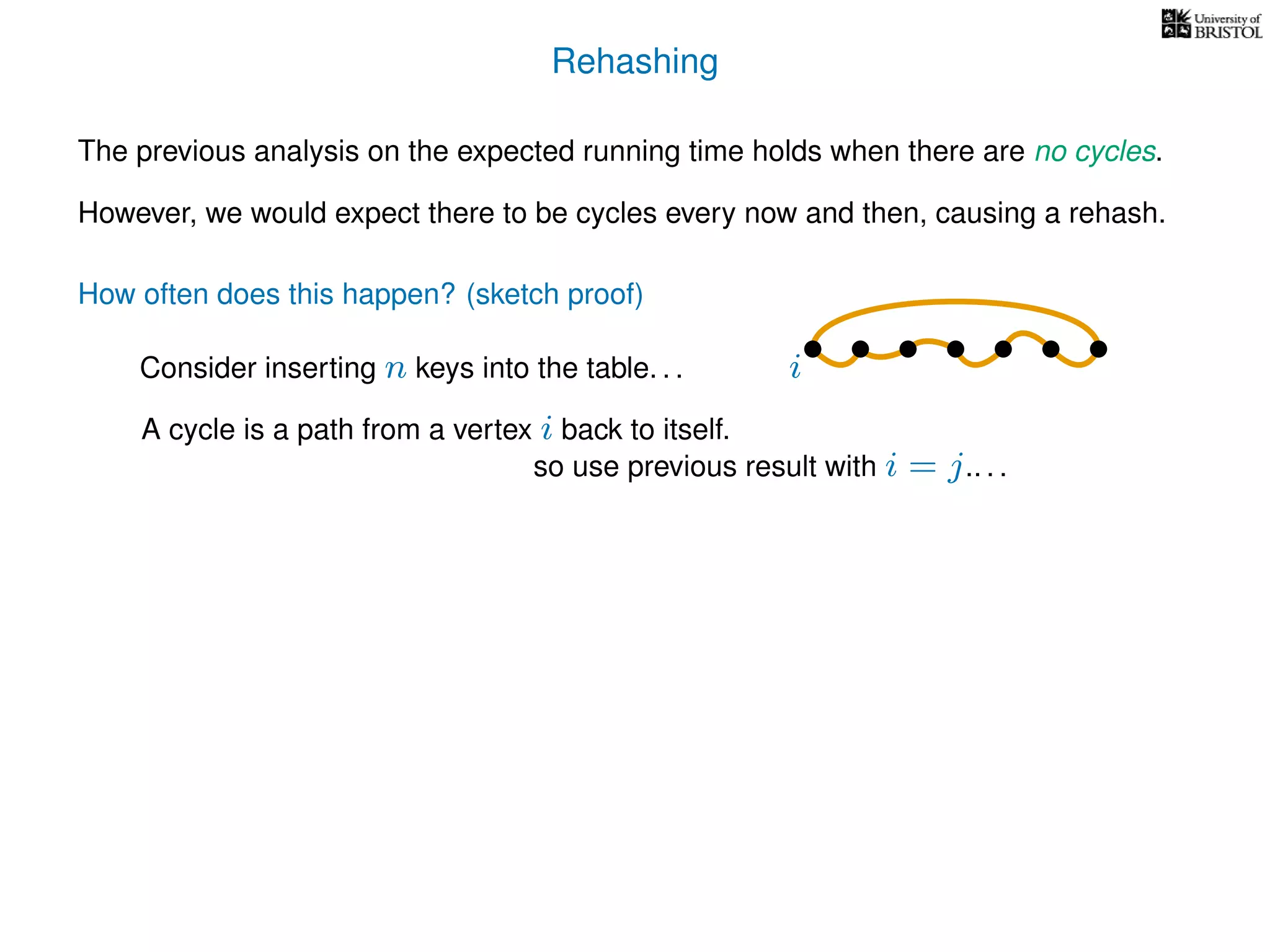
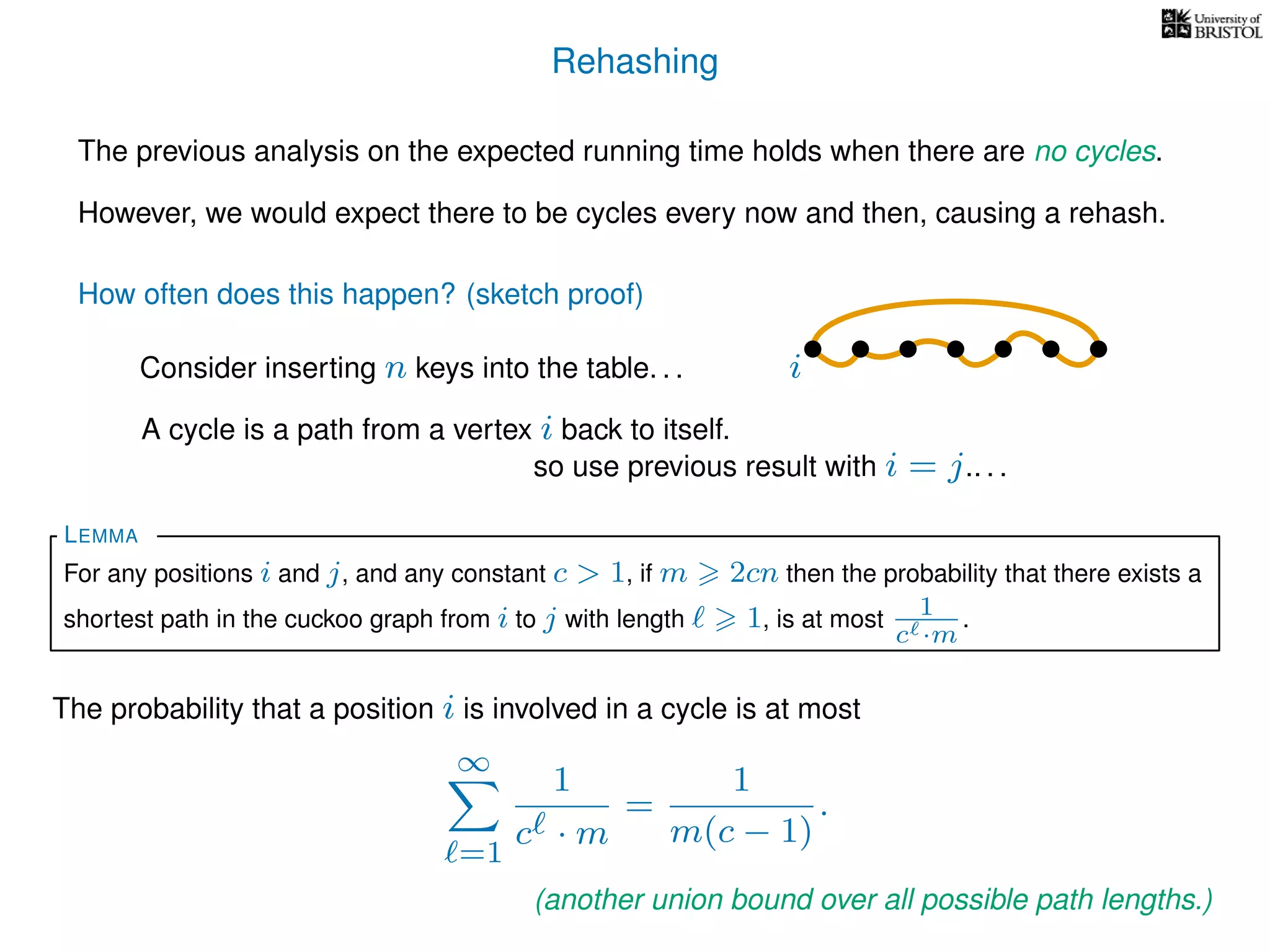
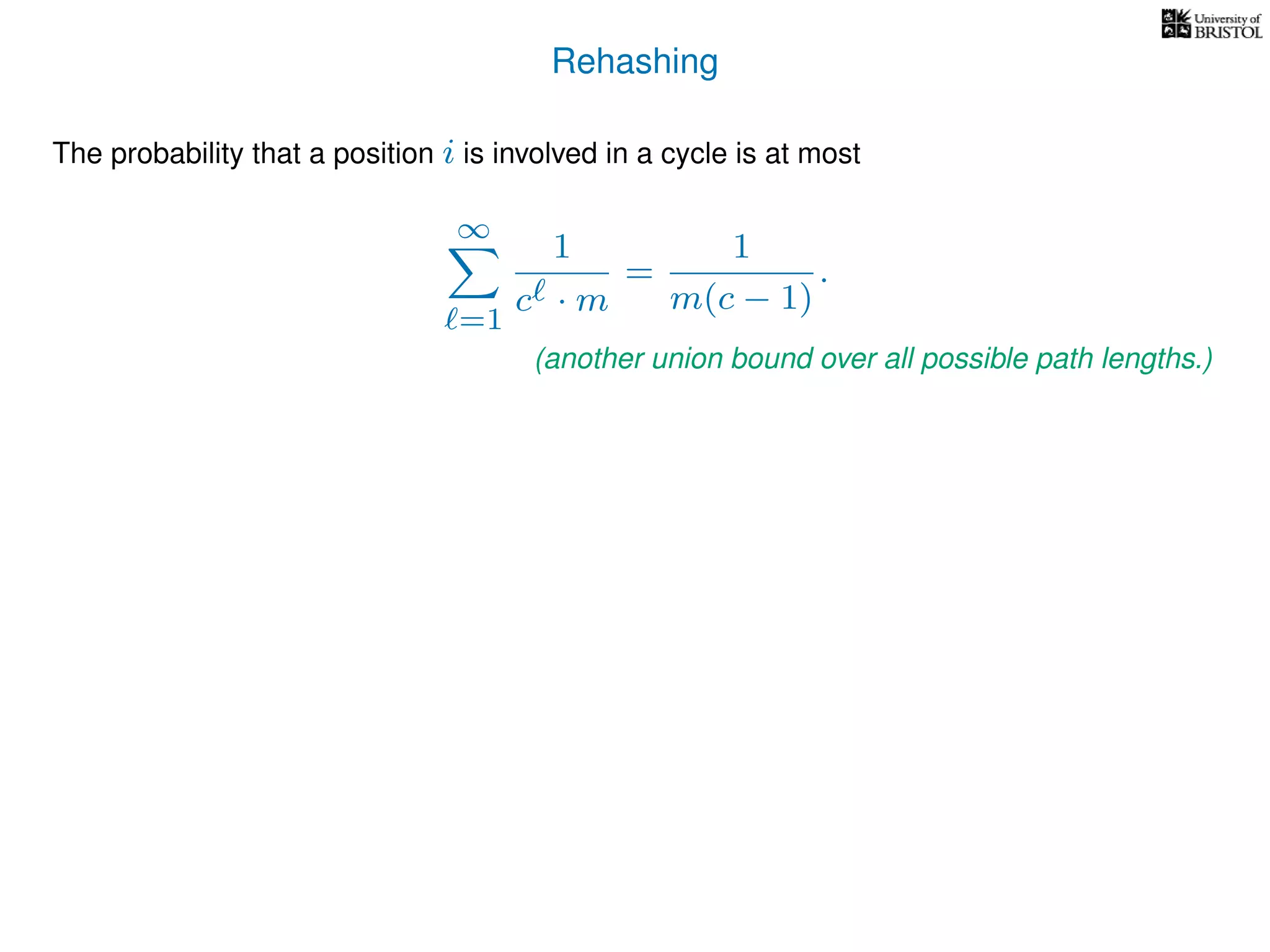
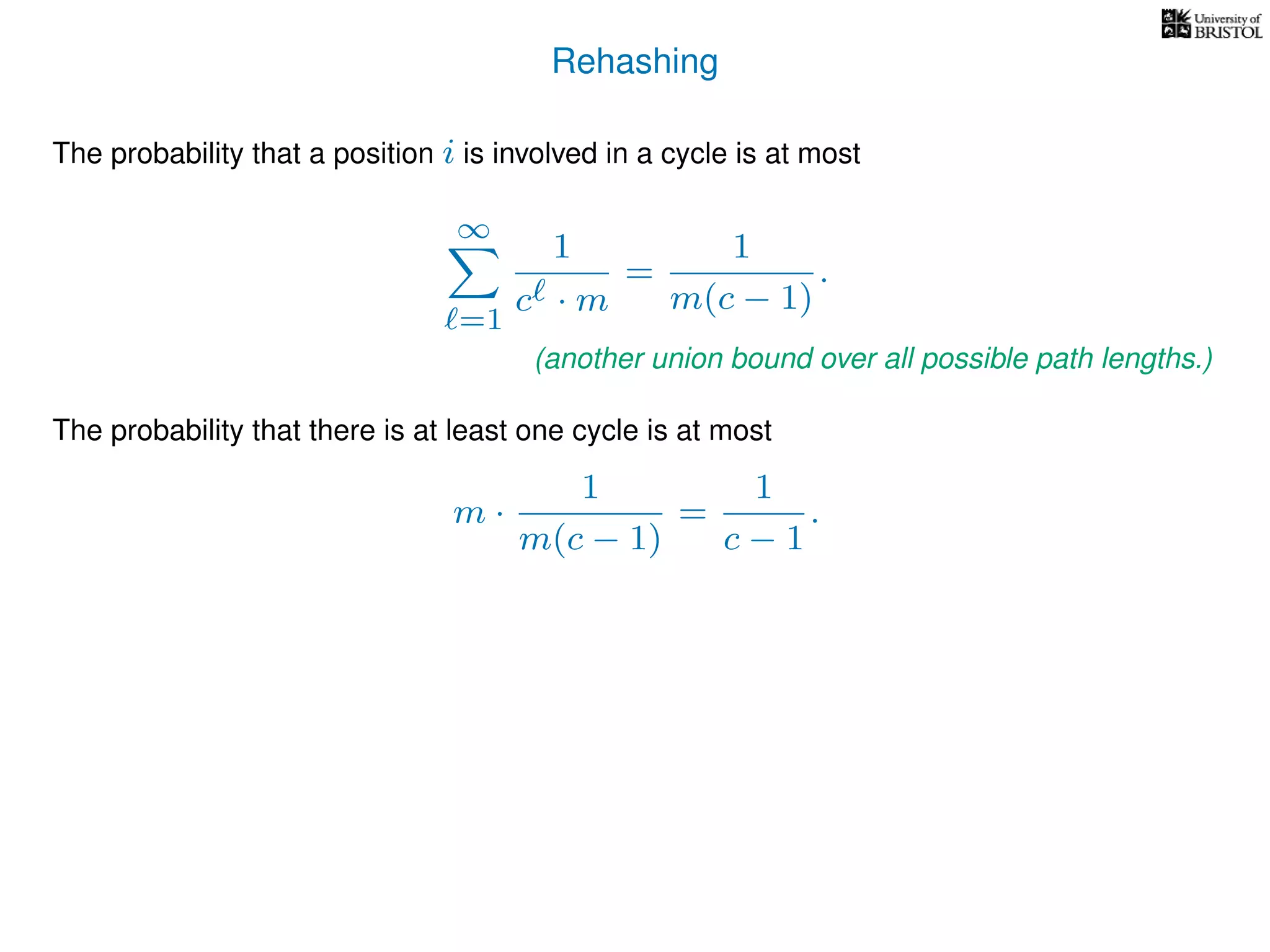
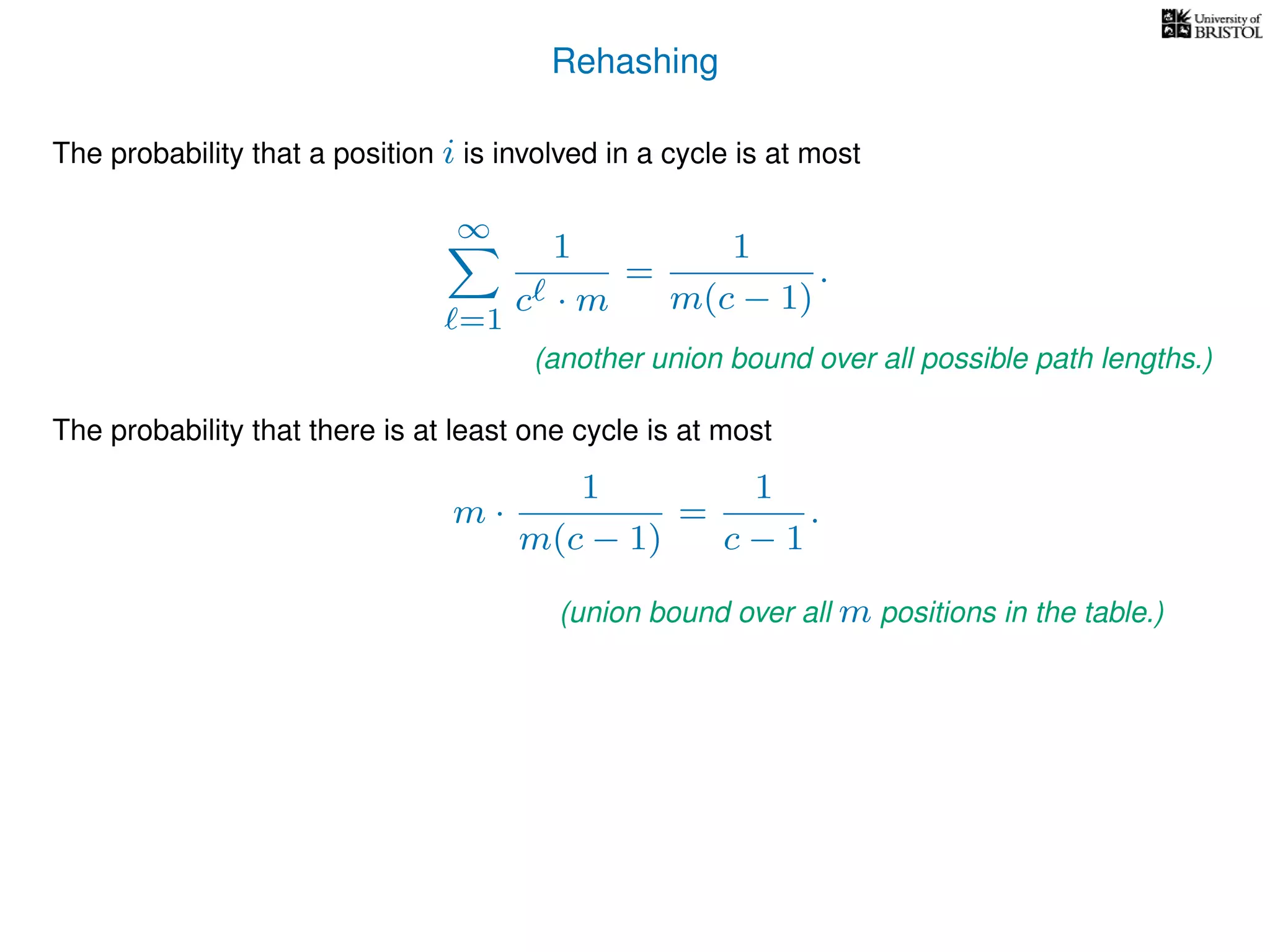
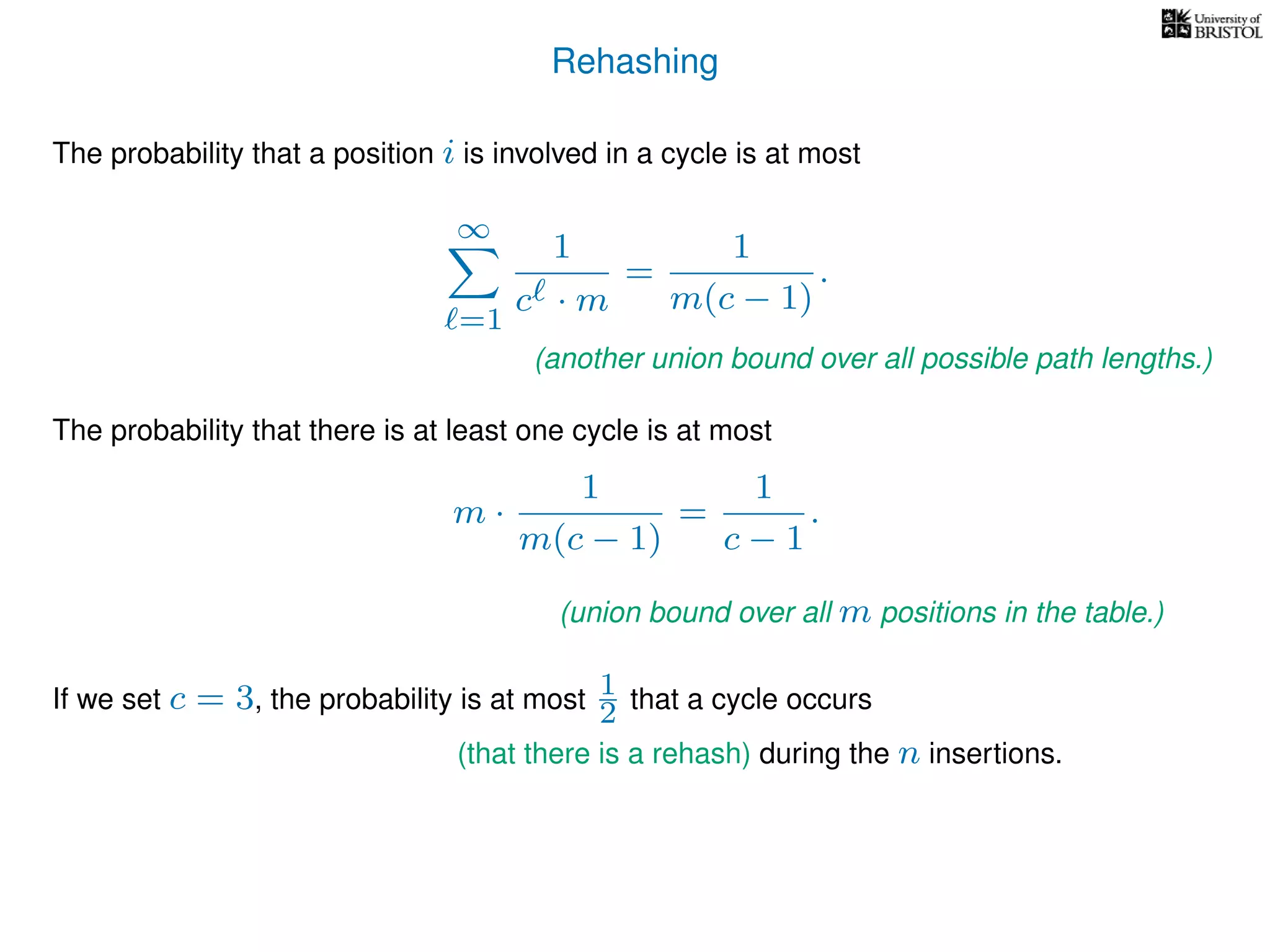
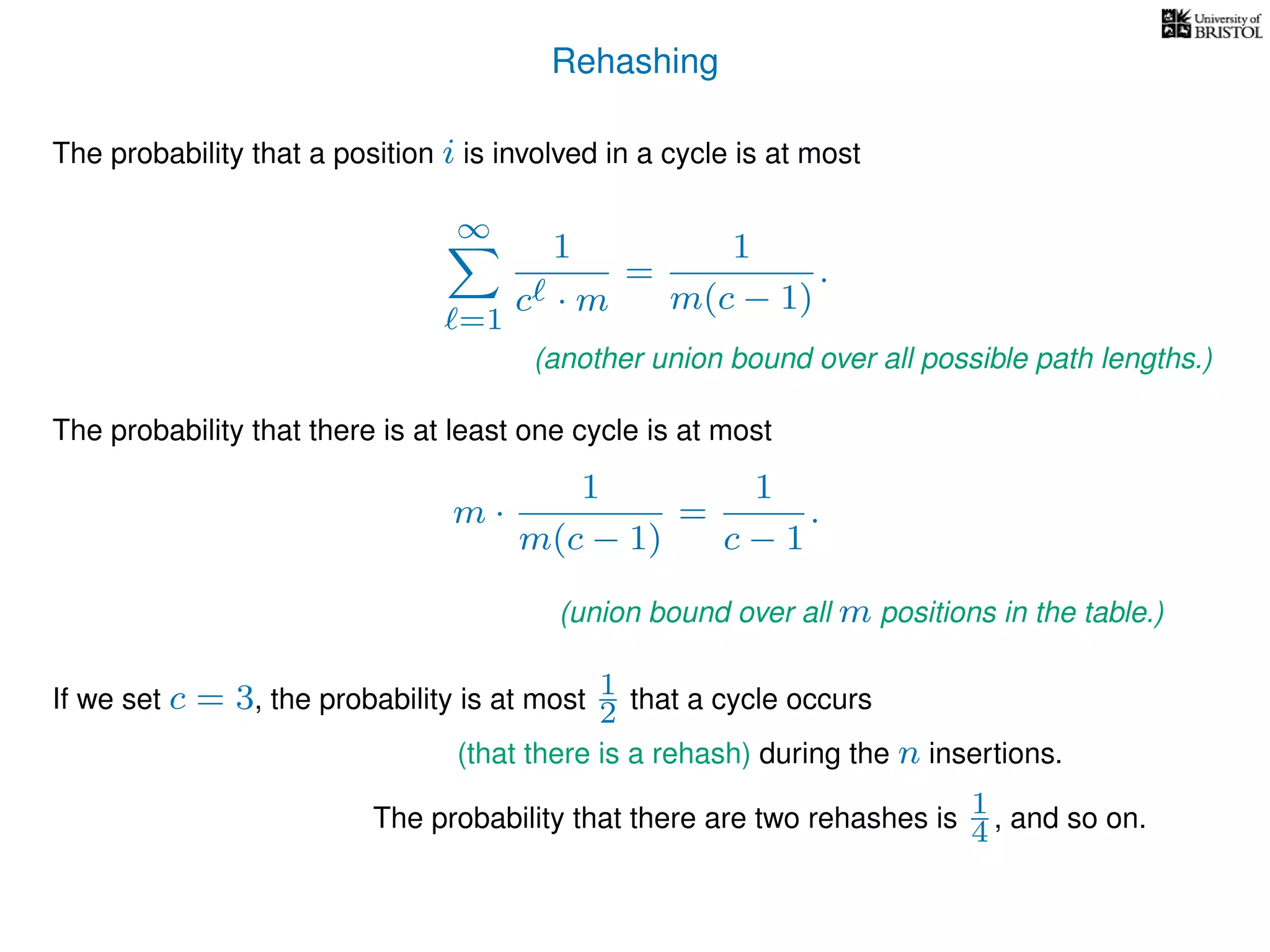
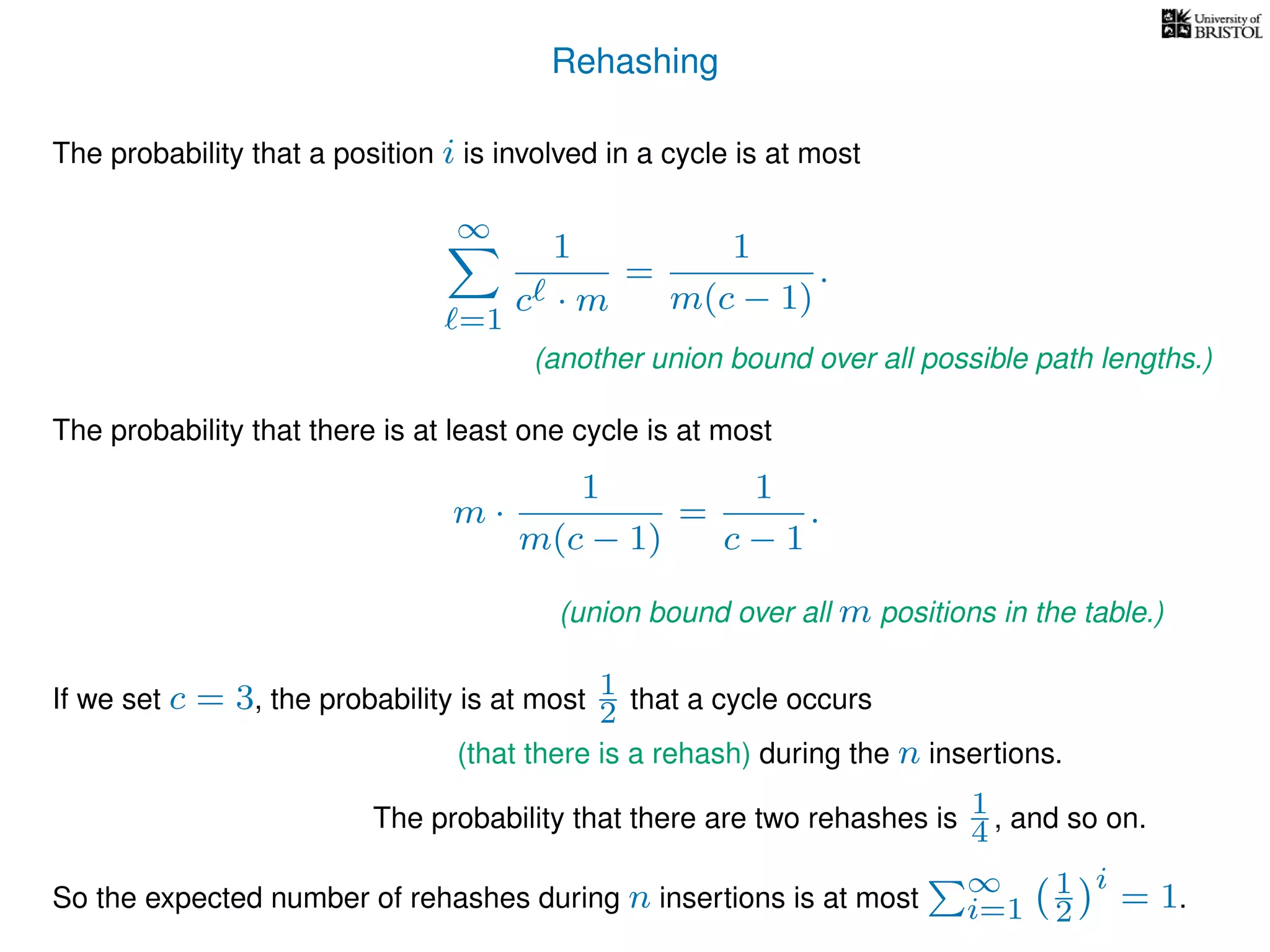
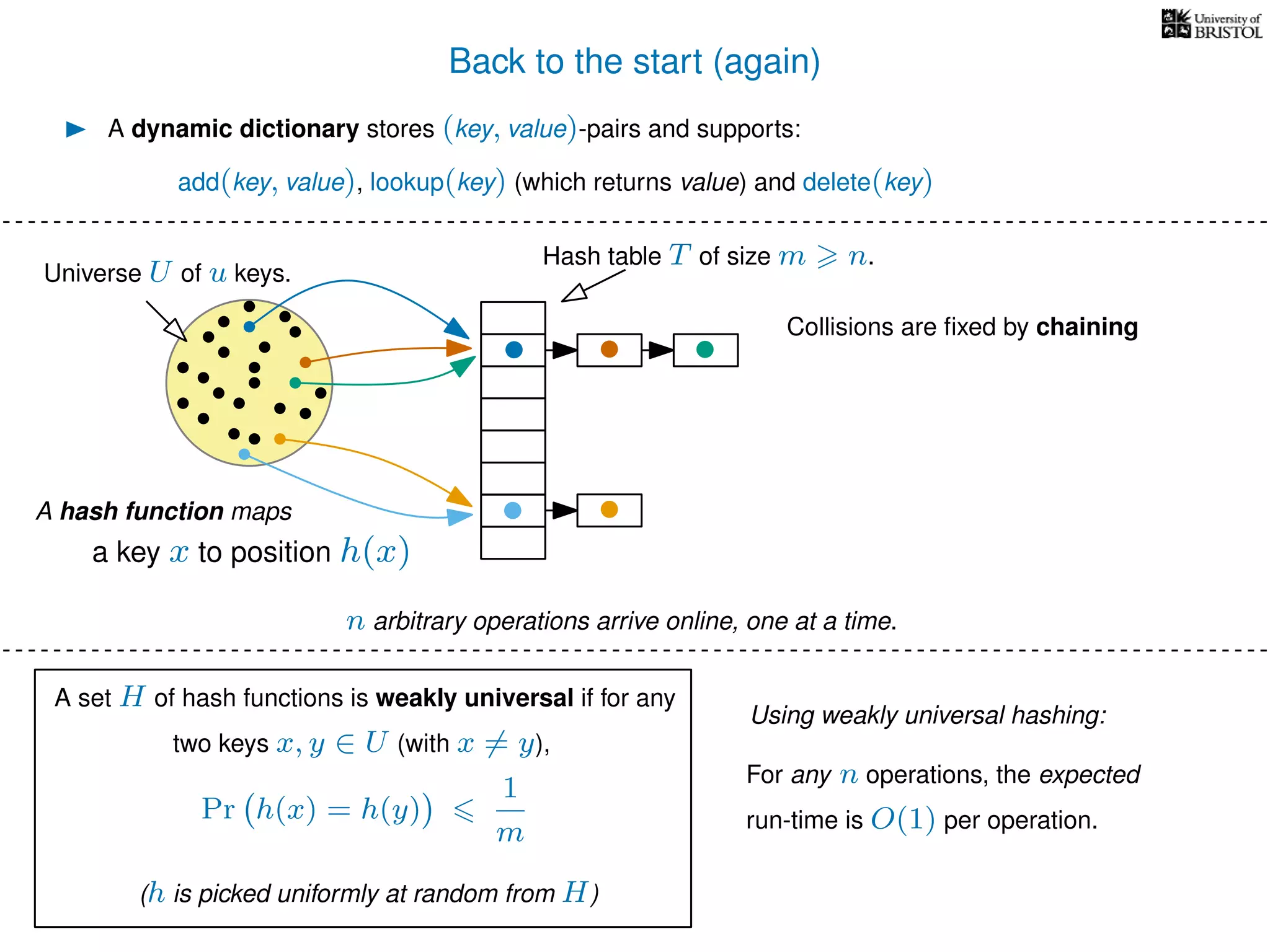
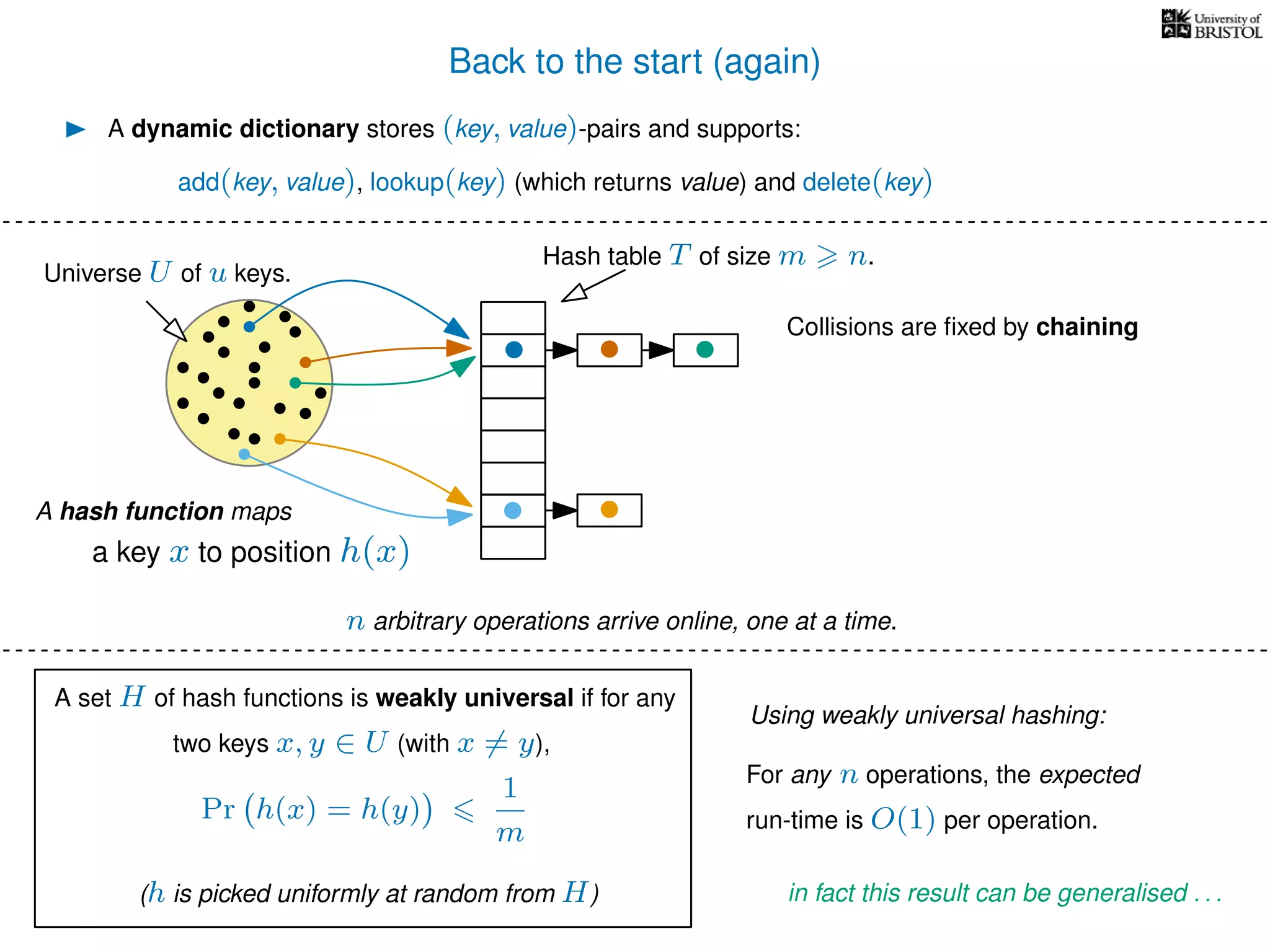
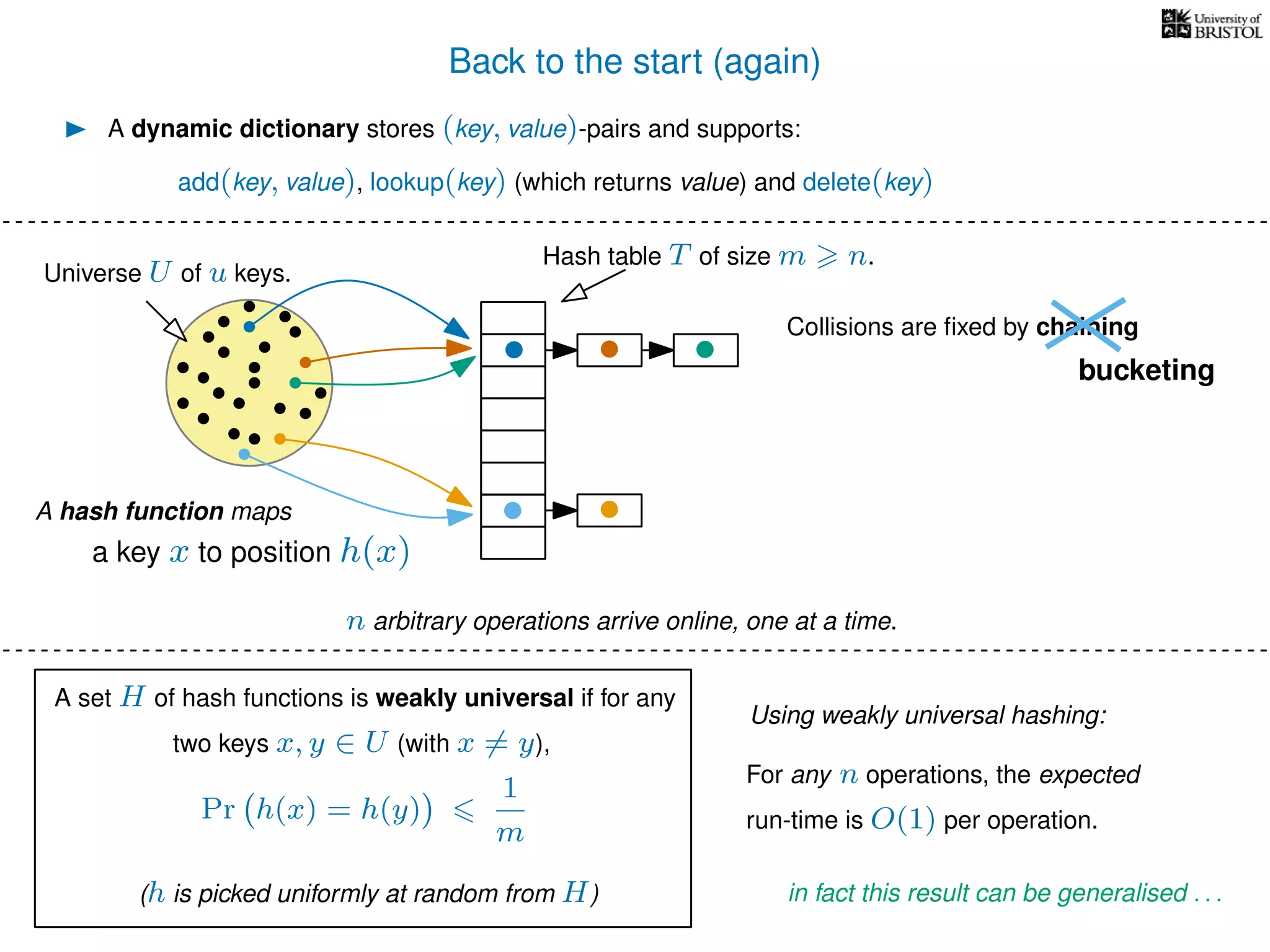
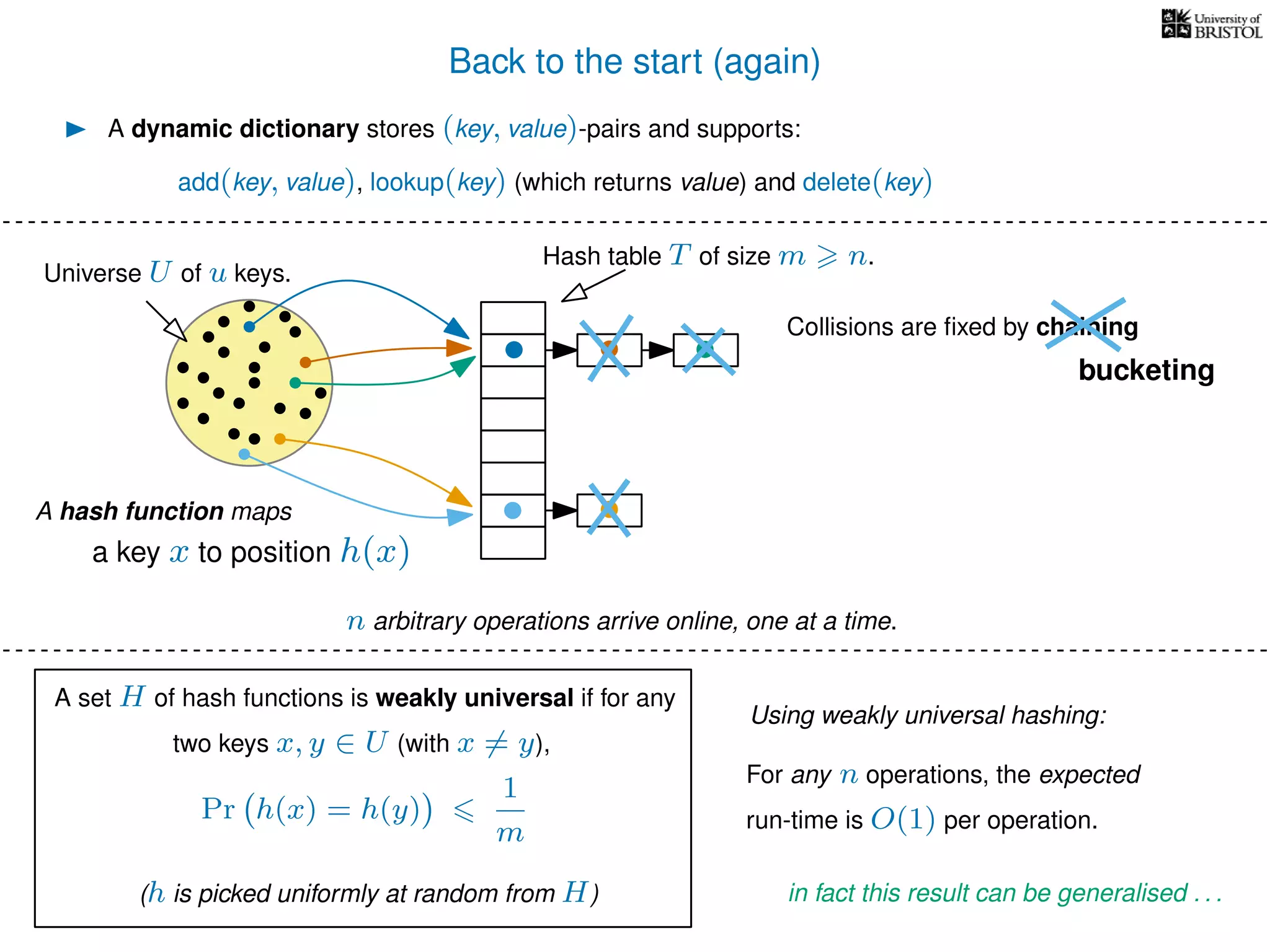
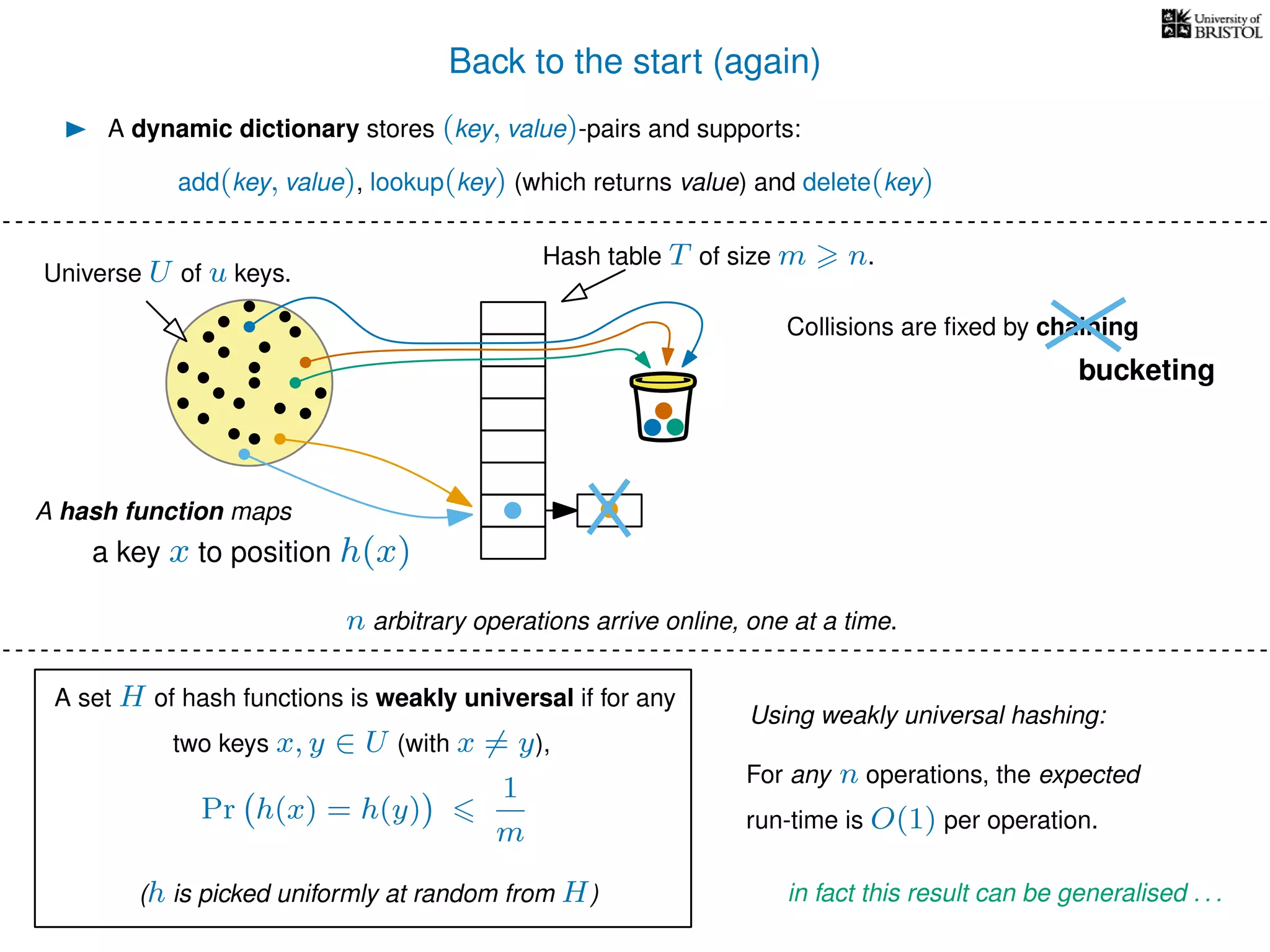
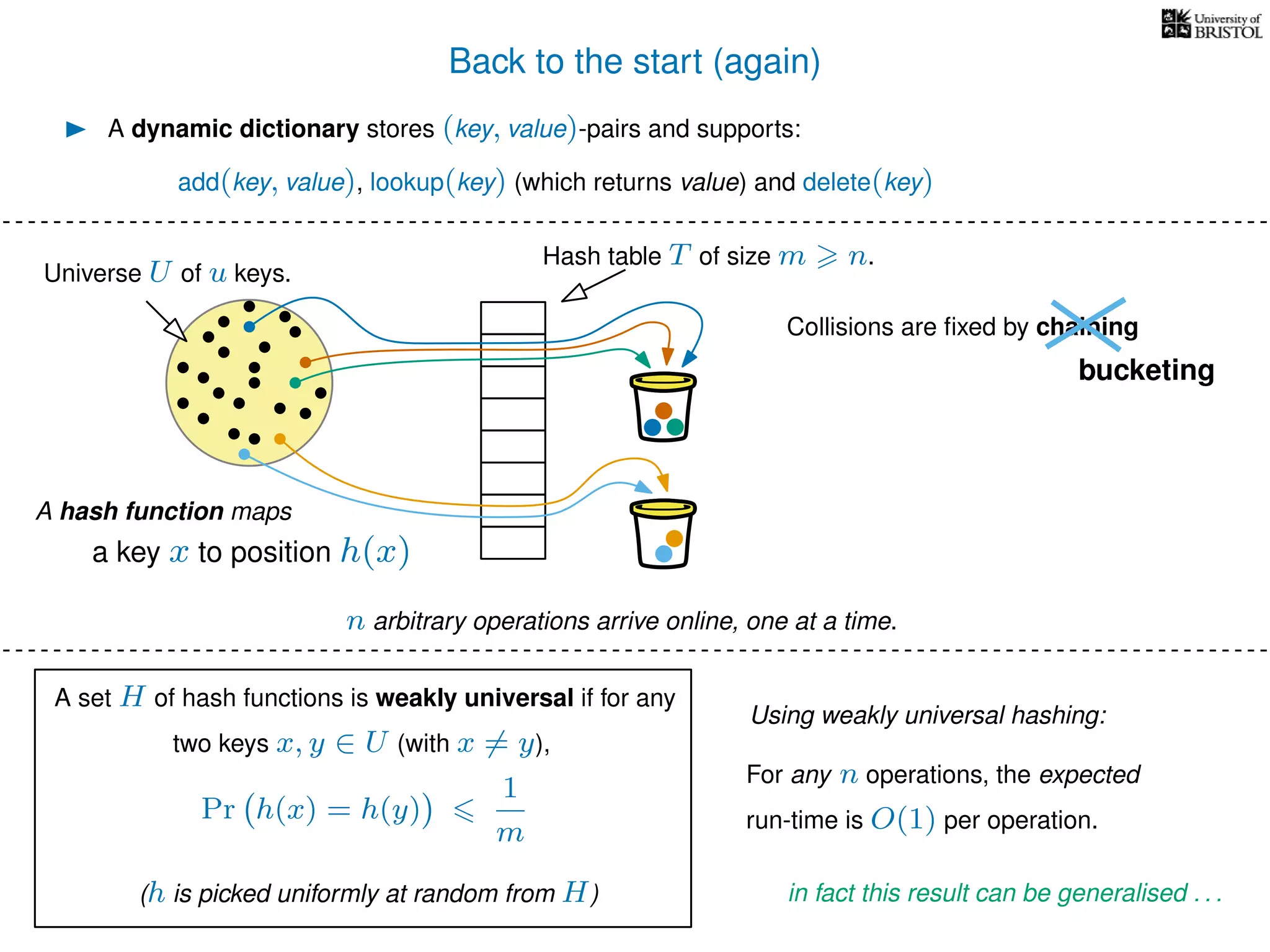
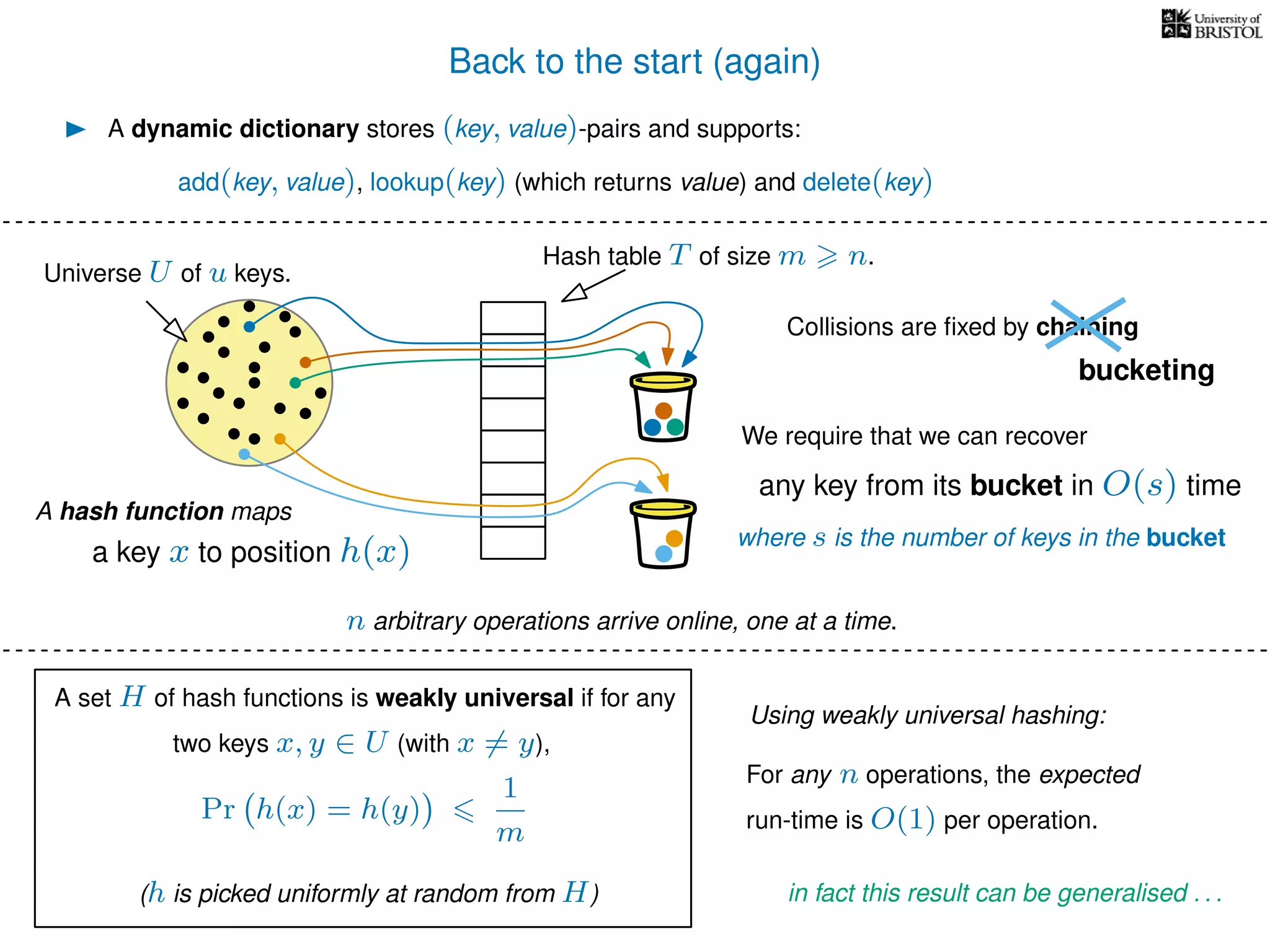
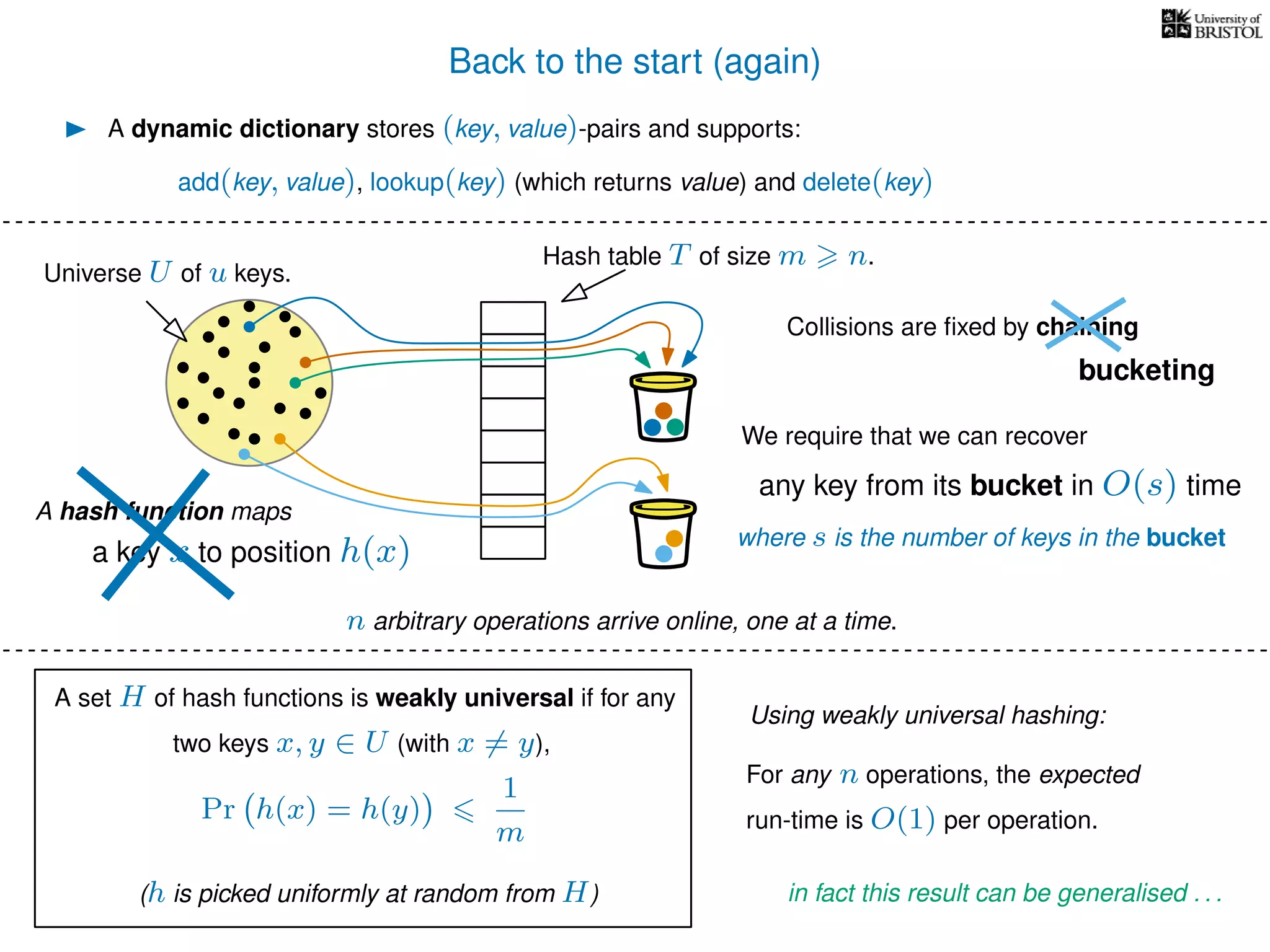
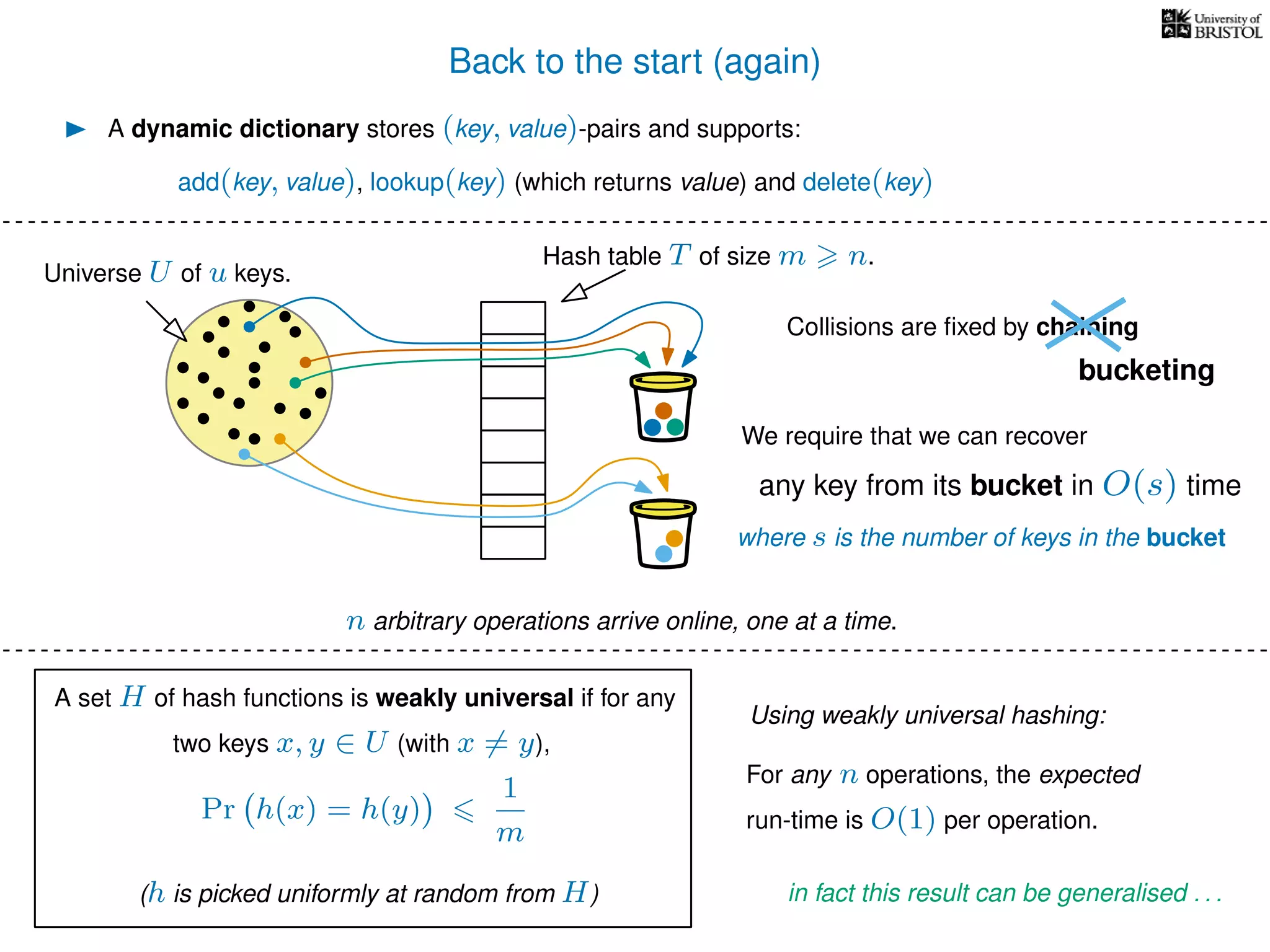
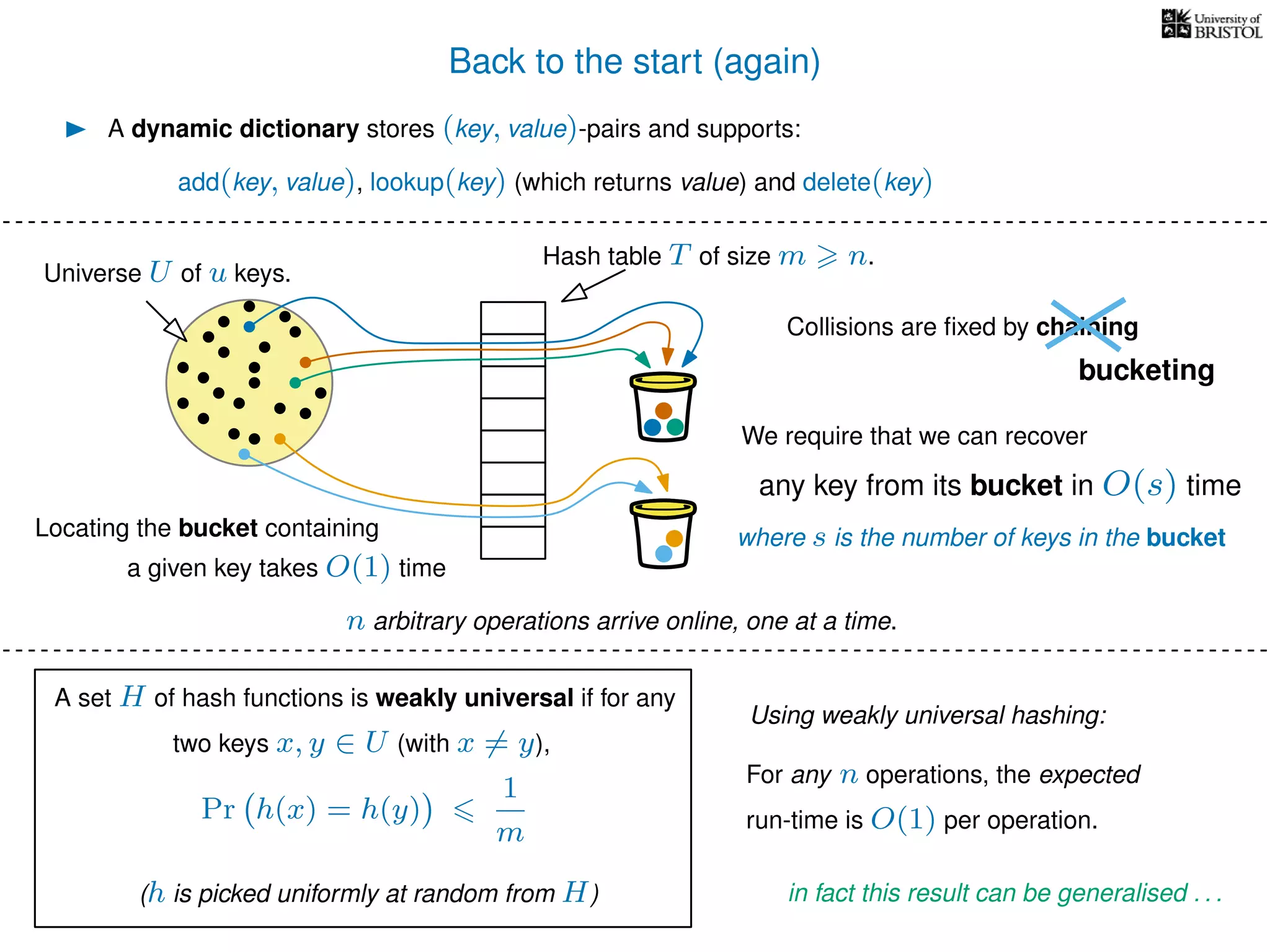
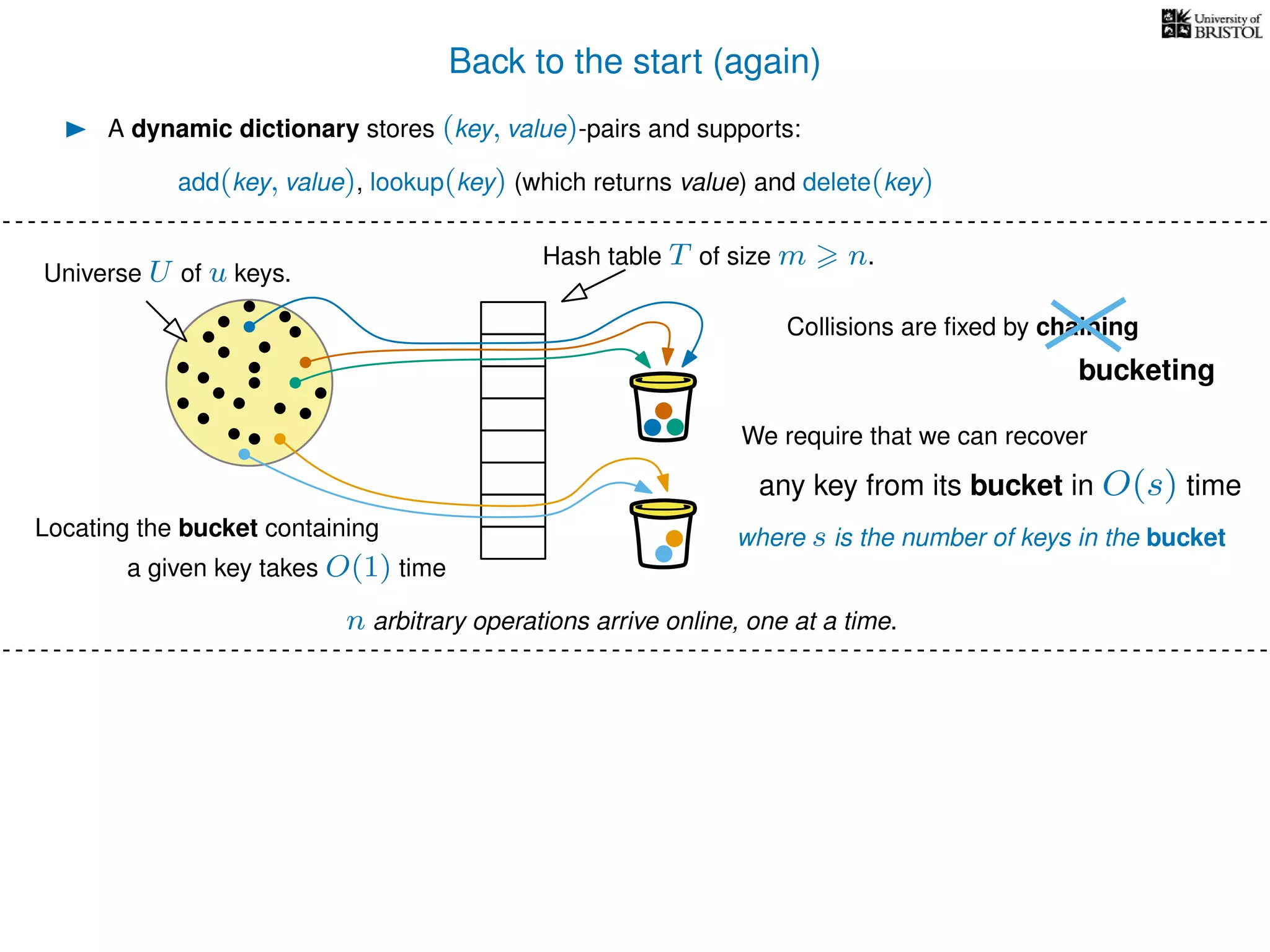
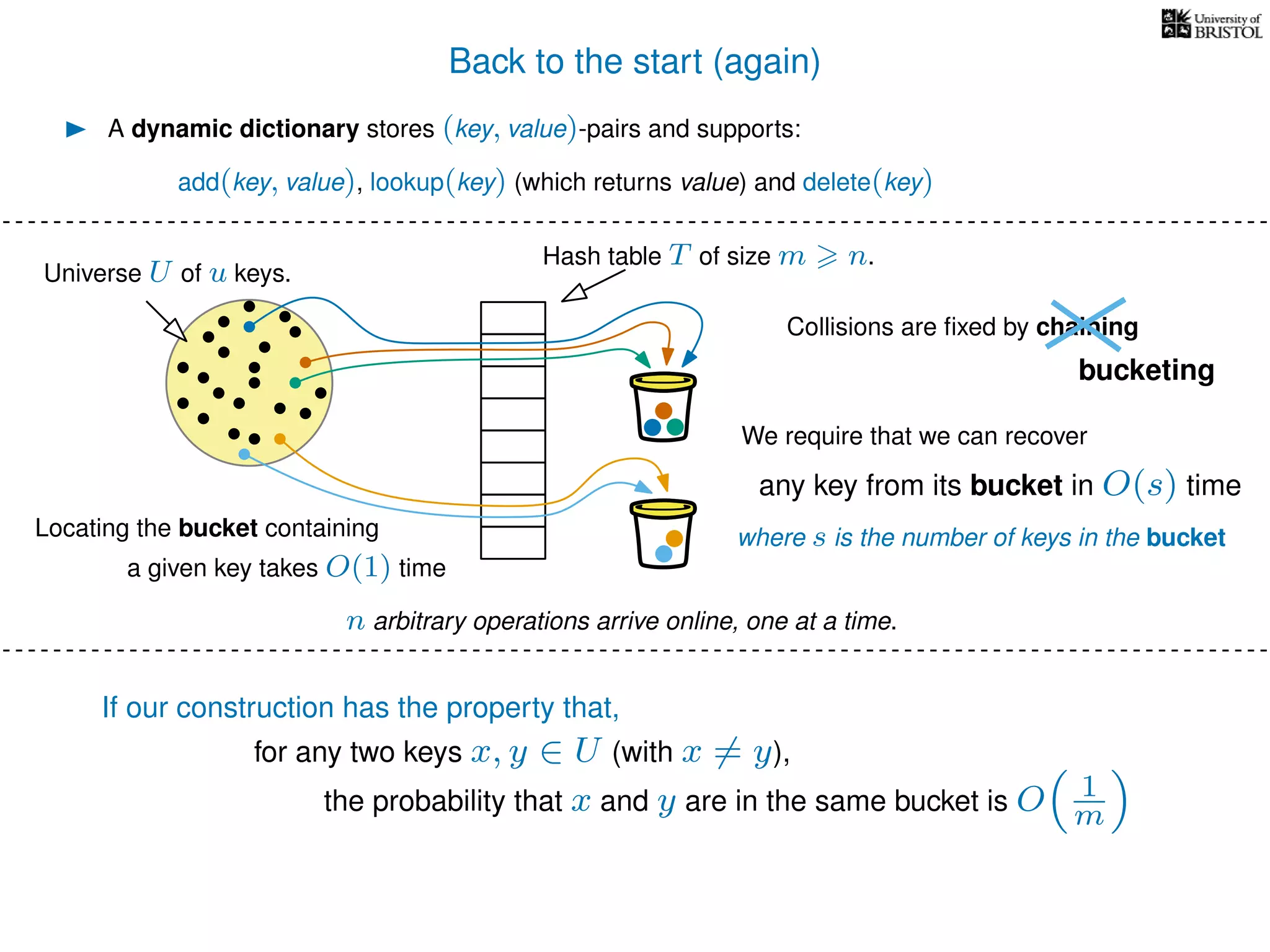
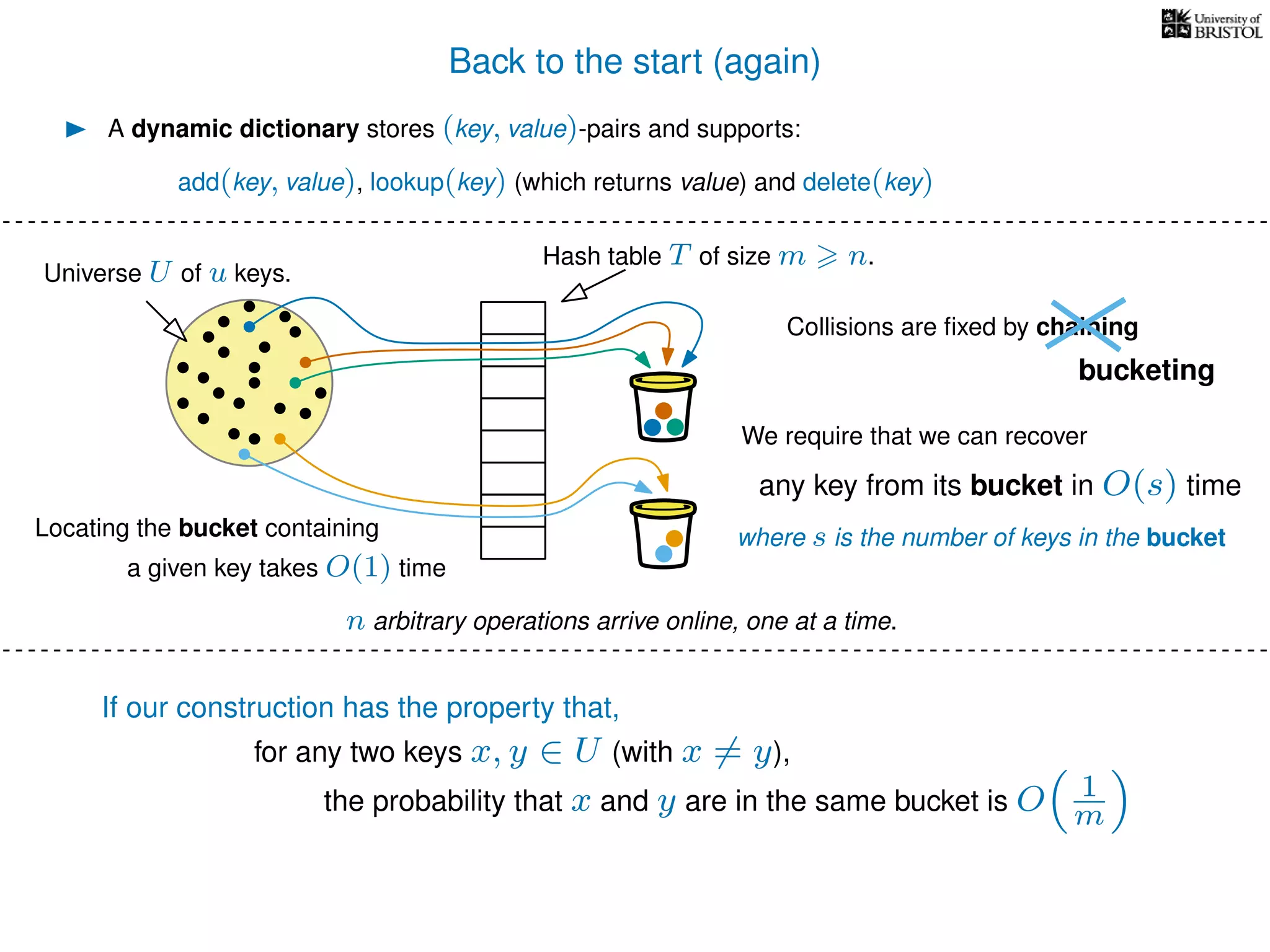
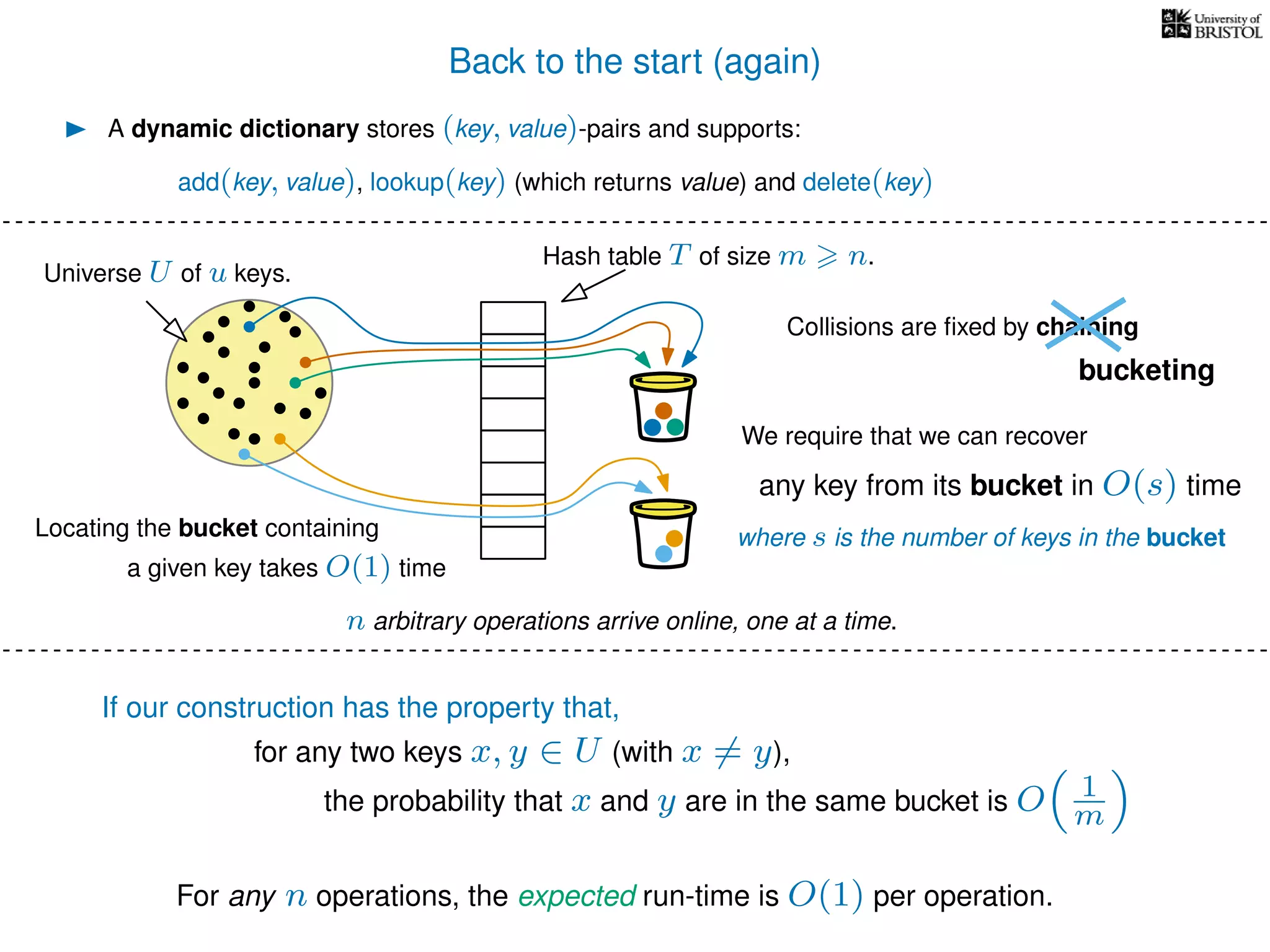
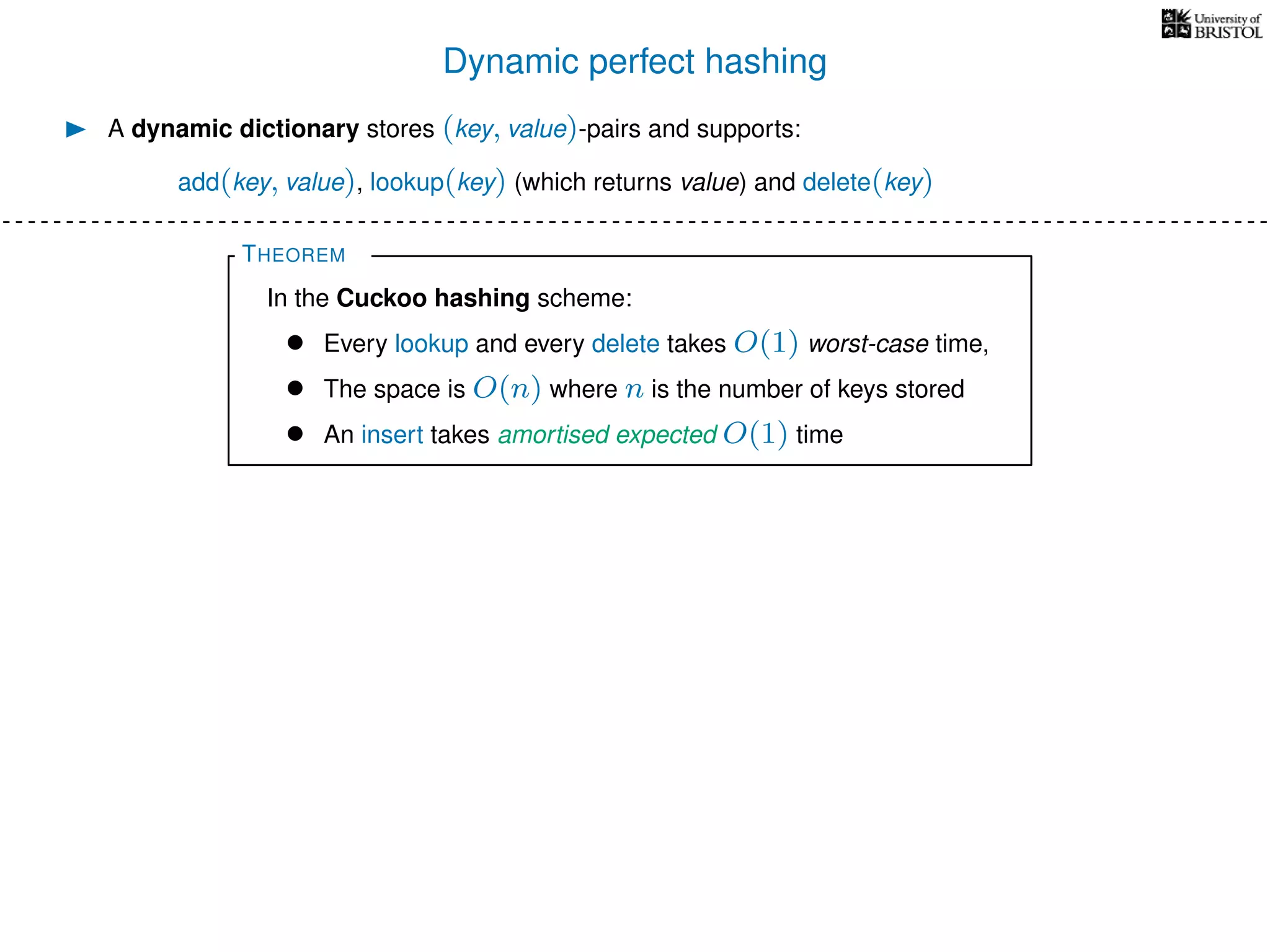
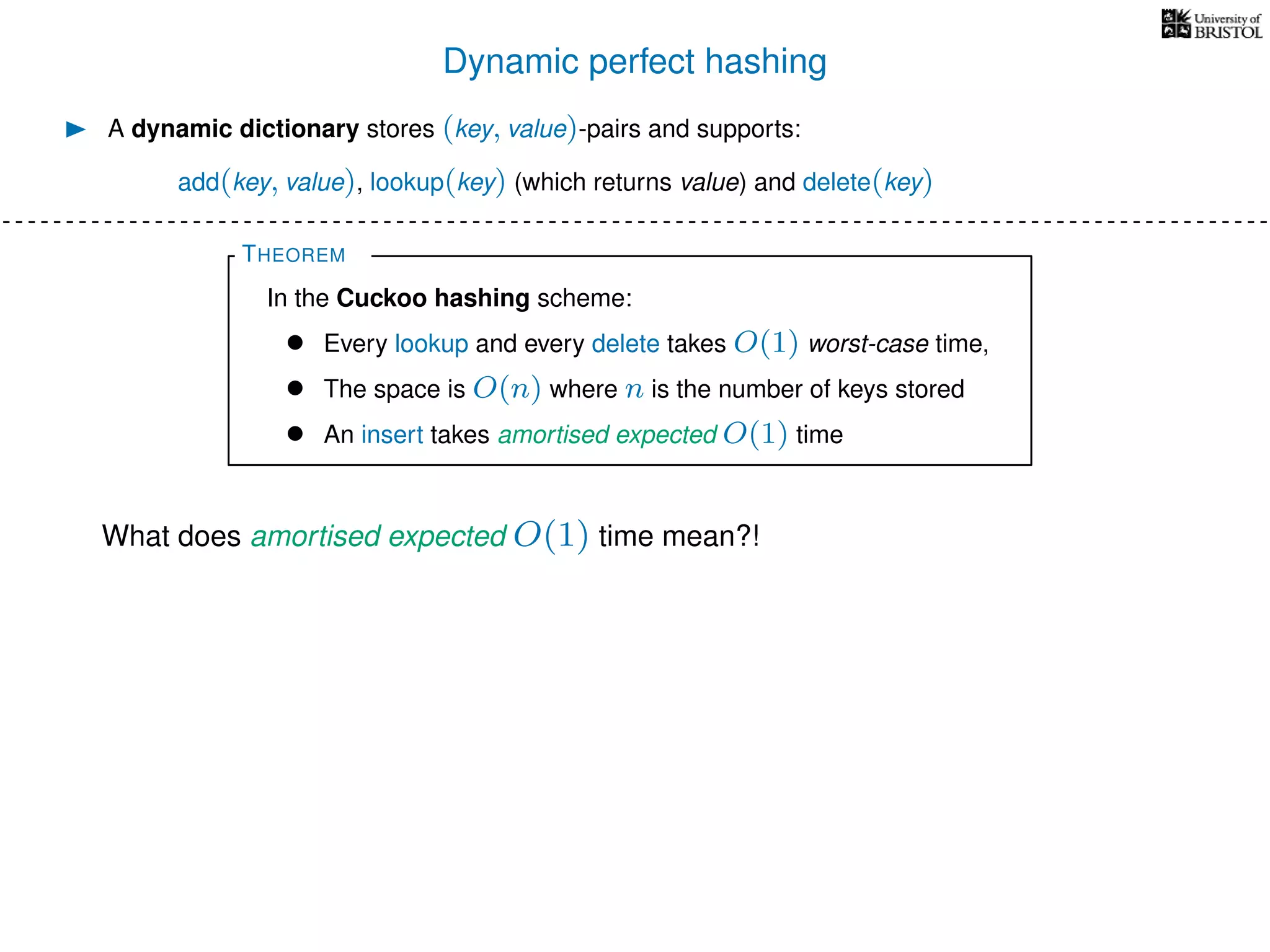
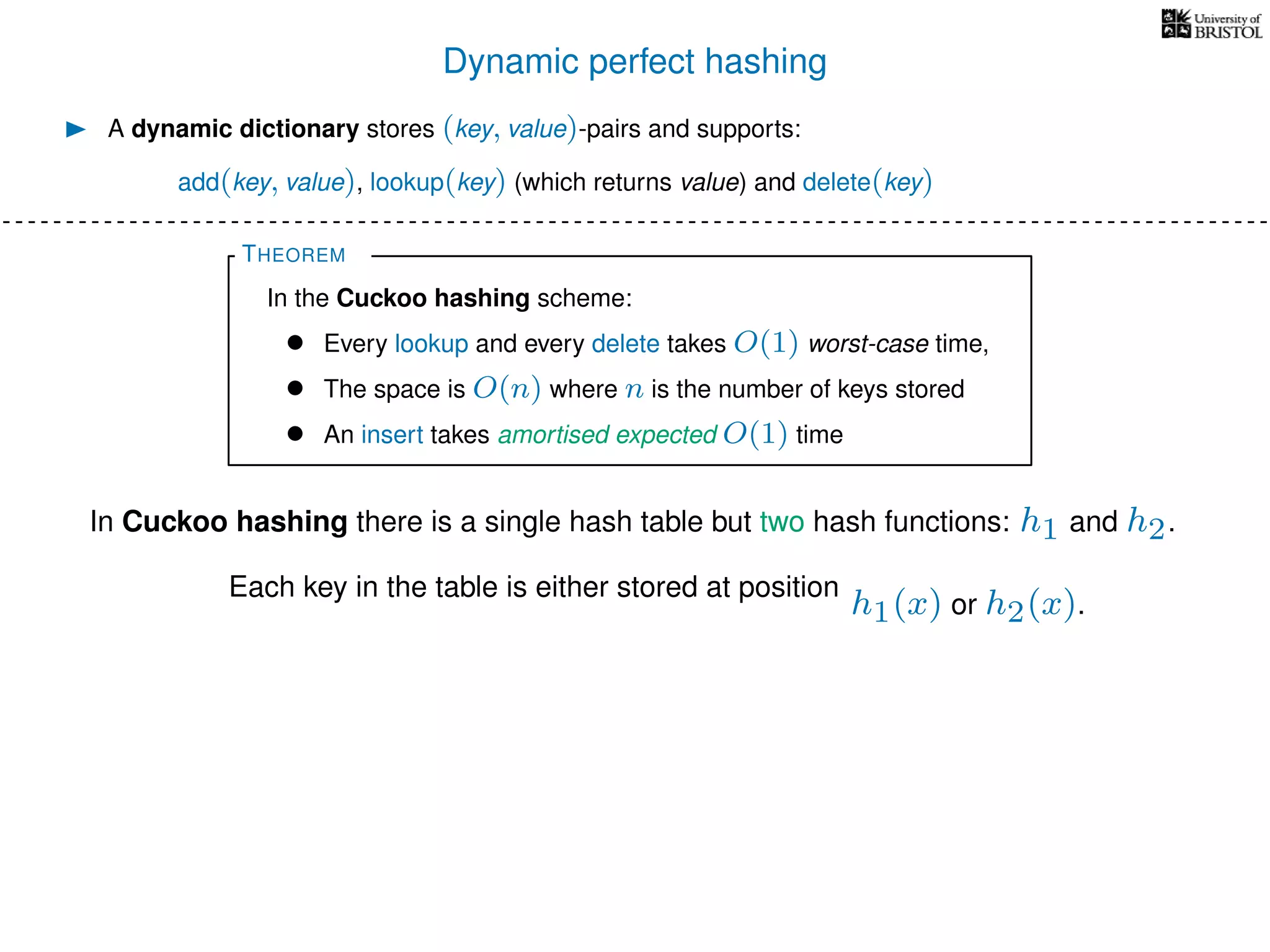
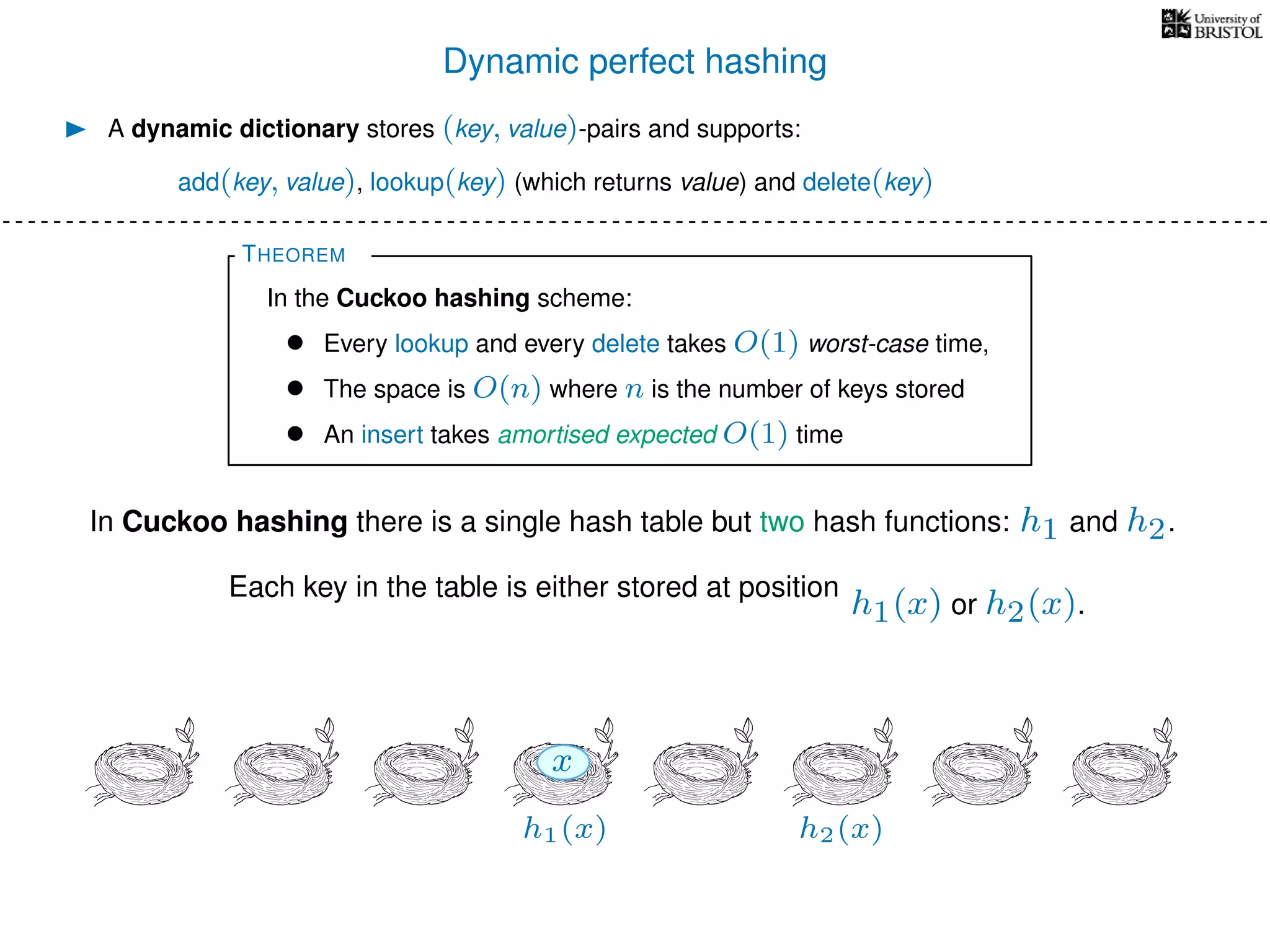
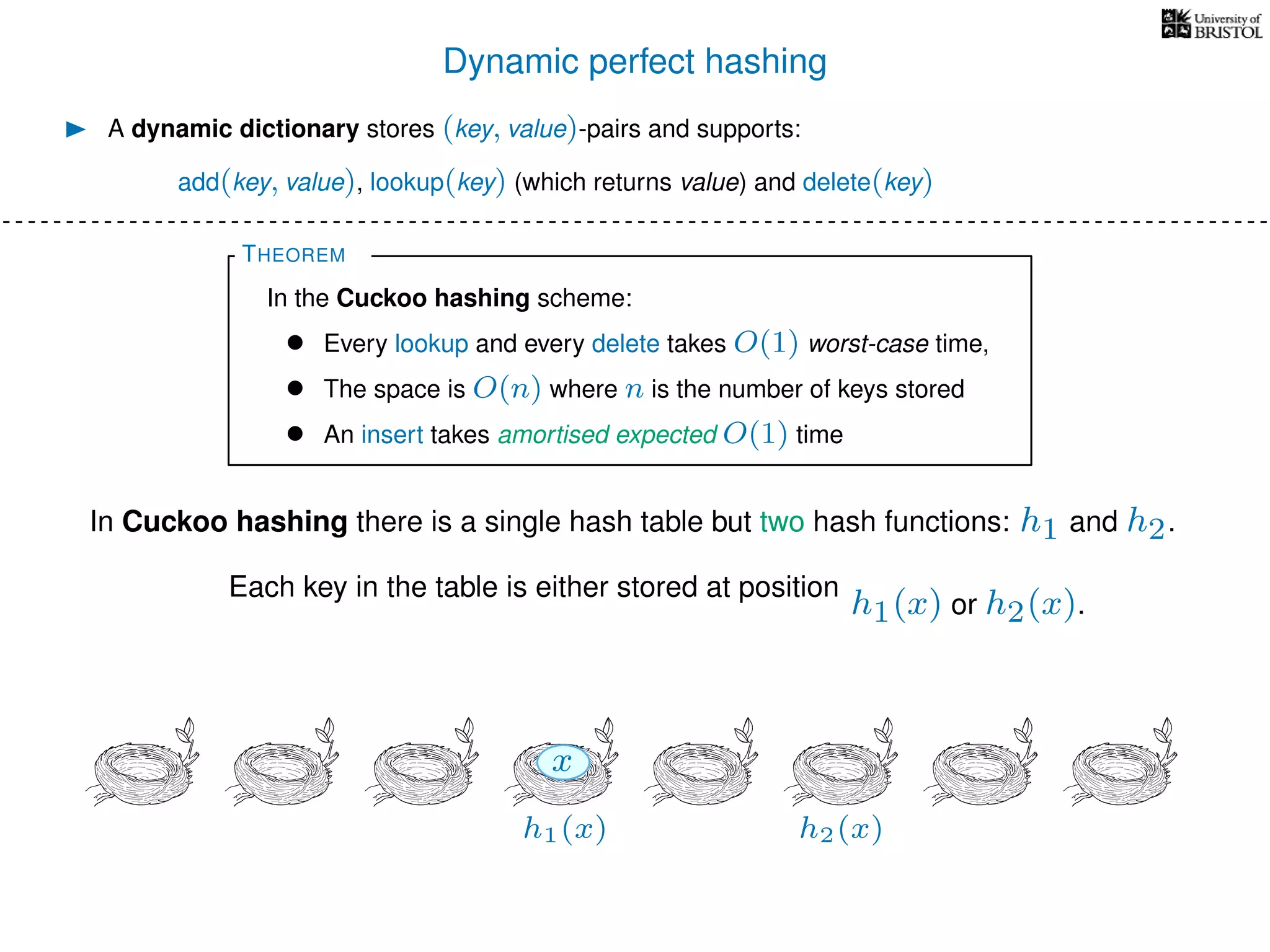
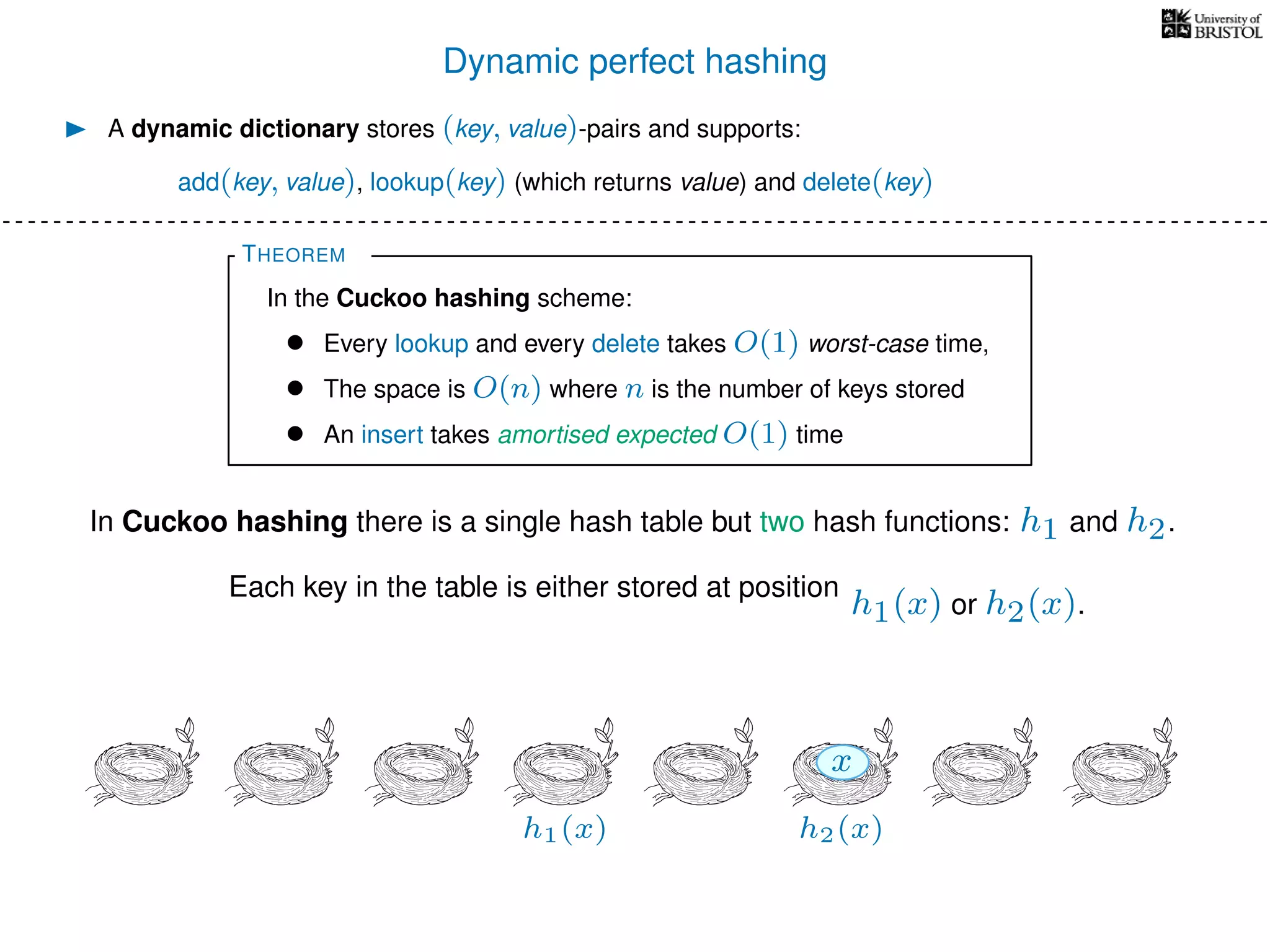
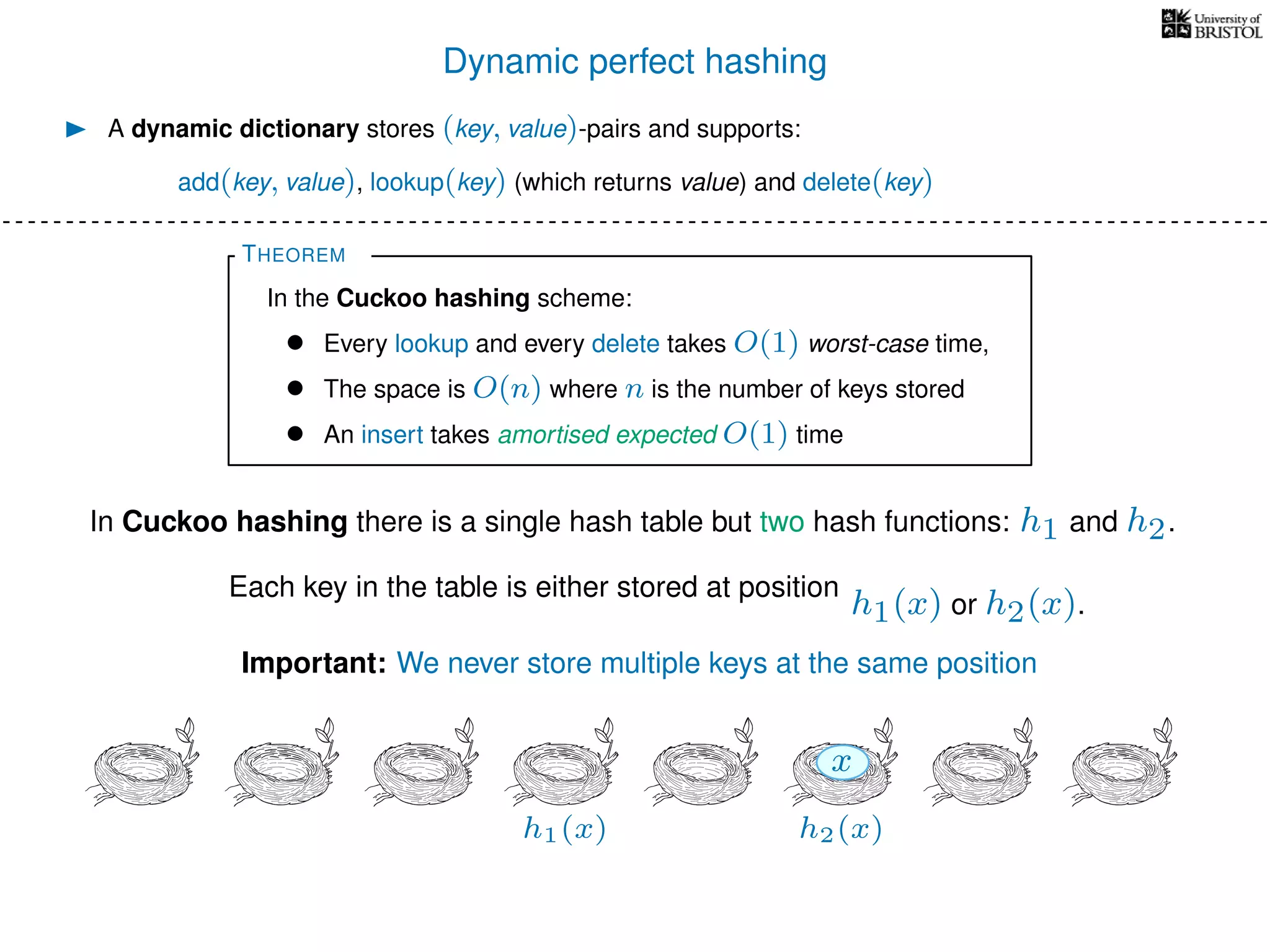
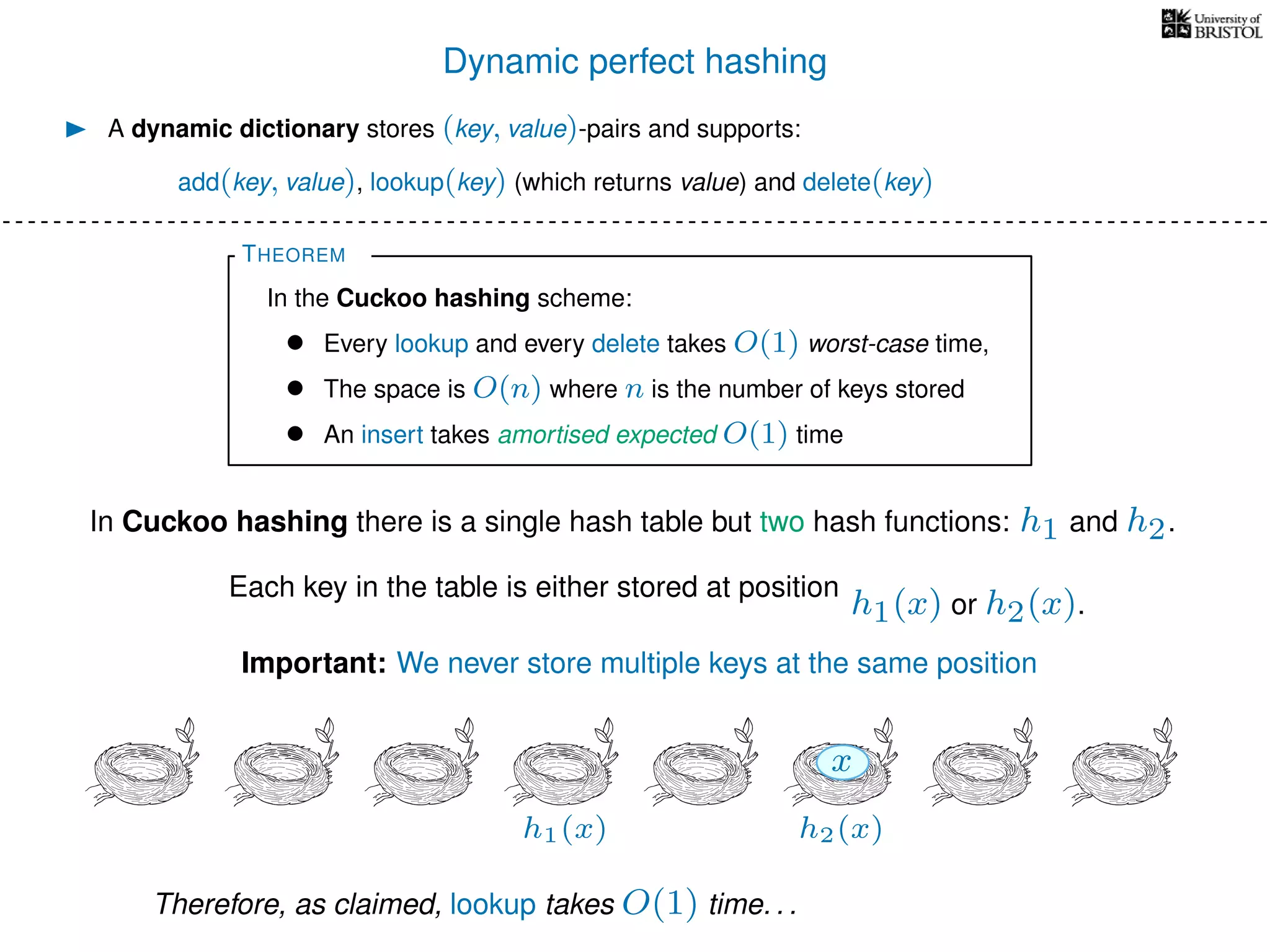
The document discusses cuckoo hashing as a method for dynamic dictionaries that store key-value pairs while supporting efficient operations like addition, lookup, and deletion. It details the expected runtime of these operations as O(1) using weakly universal hashing and highlights that in this scheme, every lookup and delete takes O(1) worst-case time with space complexity of O(n). Additionally, it explains the concept of amortized expected time for insertions and the role of multiple hash functions in cuckoo hashing.

1. Advanced Algorithms – COMS31900
Hashing part three
Cuckoo Hashing
(based on slides by Markus Jalsenius)
Benjamin Sach

2. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
A hash function maps
For any n operations, the expected
run-time is O(1) per operation.
Using weakly universal hashing:
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
a key x to position h(x)
A set H of hash functions is weakly universal if for any
two keys x, y ∈ U (with x = y),
Pr h(x) = h(y)
1
m
(h is picked uniformly at random from H)

3. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
A hash function maps
For any n operations, the expected
run-time is O(1) per operation.
Using weakly universal hashing:
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
in fact this result can be generalised . . .
a key x to position h(x)
A set H of hash functions is weakly universal if for any
two keys x, y ∈ U (with x = y),
Pr h(x) = h(y)
1
m
(h is picked uniformly at random from H)

4. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
A hash function maps
For any n operations, the expected
run-time is O(1) per operation.
Using weakly universal hashing:
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
in fact this result can be generalised . . .
a key x to position h(x)
bucketing
A set H of hash functions is weakly universal if for any
two keys x, y ∈ U (with x = y),
Pr h(x) = h(y)
1
m
(h is picked uniformly at random from H)

5. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
A hash function maps
For any n operations, the expected
run-time is O(1) per operation.
Using weakly universal hashing:
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
in fact this result can be generalised . . .
a key x to position h(x)
bucketing
A set H of hash functions is weakly universal if for any
two keys x, y ∈ U (with x = y),
Pr h(x) = h(y)
1
m
(h is picked uniformly at random from H)

6. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
A hash function maps
For any n operations, the expected
run-time is O(1) per operation.
Using weakly universal hashing:
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
in fact this result can be generalised . . .
a key x to position h(x)
bucketing
A set H of hash functions is weakly universal if for any
two keys x, y ∈ U (with x = y),
Pr h(x) = h(y)
1
m
(h is picked uniformly at random from H)

7. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
A hash function maps
For any n operations, the expected
run-time is O(1) per operation.
Using weakly universal hashing:
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
in fact this result can be generalised . . .
a key x to position h(x)
bucketing
A set H of hash functions is weakly universal if for any
two keys x, y ∈ U (with x = y),
Pr h(x) = h(y)
1
m
(h is picked uniformly at random from H)

8. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
A hash function maps
For any n operations, the expected
run-time is O(1) per operation.
Using weakly universal hashing:
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
in fact this result can be generalised . . .
a key x to position h(x)
bucketing
We require that we can recover
any key from its bucket in O(s) time
where s is the number of keys in the bucket
A set H of hash functions is weakly universal if for any
two keys x, y ∈ U (with x = y),
Pr h(x) = h(y)
1
m
(h is picked uniformly at random from H)

9. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
A hash function maps
For any n operations, the expected
run-time is O(1) per operation.
Using weakly universal hashing:
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
in fact this result can be generalised . . .
a key x to position h(x)
bucketing
We require that we can recover
any key from its bucket in O(s) time
where s is the number of keys in the bucket
A set H of hash functions is weakly universal if for any
two keys x, y ∈ U (with x = y),
Pr h(x) = h(y)
1
m
(h is picked uniformly at random from H)

10. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
For any n operations, the expected
run-time is O(1) per operation.
Using weakly universal hashing:
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
in fact this result can be generalised . . .
bucketing
We require that we can recover
any key from its bucket in O(s) time
where s is the number of keys in the bucket
A set H of hash functions is weakly universal if for any
two keys x, y ∈ U (with x = y),
Pr h(x) = h(y)
1
m
(h is picked uniformly at random from H)

11. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
For any n operations, the expected
run-time is O(1) per operation.
Using weakly universal hashing:
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
in fact this result can be generalised . . .
bucketing
We require that we can recover
any key from its bucket in O(s) time
where s is the number of keys in the bucket
A set H of hash functions is weakly universal if for any
two keys x, y ∈ U (with x = y),
Pr h(x) = h(y)
1
m
(h is picked uniformly at random from H)
Locating the bucket containing
a given key takes O(1) time

12. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
bucketing
We require that we can recover
any key from its bucket in O(s) time
where s is the number of keys in the bucketLocating the bucket containing
a given key takes O(1) time

13. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
bucketing
We require that we can recover
any key from its bucket in O(s) time
where s is the number of keys in the bucket
If our construction has the property that,
for any two keys x, y ∈ U (with x = y),
the probability that x and y are in the same bucket is O 1
m
Locating the bucket containing
a given key takes O(1) time

14. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
bucketing
We require that we can recover
any key from its bucket in O(s) time
where s is the number of keys in the bucket
If our construction has the property that,
for any two keys x, y ∈ U (with x = y),
the probability that x and y are in the same bucket is O 1
m
Locating the bucket containing
a given key takes O(1) time

15. Back to the start (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
bucketing
We require that we can recover
any key from its bucket in O(s) time
where s is the number of keys in the bucket
If our construction has the property that,
for any two keys x, y ∈ U (with x = y),
the probability that x and y are in the same bucket is O 1
m
For any n operations, the expected run-time is O(1) per operation.
Locating the bucket containing
a given key takes O(1) time

16. Dynamic perfect hashing
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time

17. Dynamic perfect hashing
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
What does amortised expected O(1) time mean?!

18. Dynamic perfect hashing
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
What does amortised expected O(1) time mean?!
let’s build it up. . .

19. Dynamic perfect hashing
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
What does amortised expected O(1) time mean?!
let’s build it up. . .
“O(1) worst-case time per operation”
means every operation takes constant time

20. Dynamic perfect hashing
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
What does amortised expected O(1) time mean?!
let’s build it up. . .
“O(1) worst-case time per operation”
means every operation takes constant time
“The total worst-case time complexity of performing any n operations is O(n)”

21. Dynamic perfect hashing
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
What does amortised expected O(1) time mean?!
let’s build it up. . .
“O(1) worst-case time per operation”
means every operation takes constant time
“The total worst-case time complexity of performing any n operations is O(n)”
this does not imply that every operation takes constant time

22. Dynamic perfect hashing
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
What does amortised expected O(1) time mean?!
let’s build it up. . .
“O(1) worst-case time per operation”
means every operation takes constant time
“The total worst-case time complexity of performing any n operations is O(n)”
this does not imply that every operation takes constant time
However, it does mean that the amortised worst-case time complexity of an operation is O(1)

23. Dynamic perfect hashing
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
What does amortised expected O(1) time mean?!
let’s build it up. . .
“O(1) worst-case time per operation”
means every operation takes constant time in expectation
“The total worst-case time complexity of performing any n operations is O(n)”
this does not imply that every operation takes constant time in expectation
However, it does mean that the amortised worst-case time complexity of an operation is O(1)
expected
expected
expected

24. Dynamic perfect hashing
In Cuckoo hashing there is a single hash table but two hash functions: h1 and h2.
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time

25. Dynamic perfect hashing
In Cuckoo hashing there is a single hash table but two hash functions: h1 and h2.
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
Each key in the table is either stored at position
h1(x) or h2(x).

26. Dynamic perfect hashing
In Cuckoo hashing there is a single hash table but two hash functions: h1 and h2.
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
Each key in the table is either stored at position
h1(x) or h2(x).
h1(x) h2(x)

27. Dynamic perfect hashing
In Cuckoo hashing there is a single hash table but two hash functions: h1 and h2.
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
Each key in the table is either stored at position
h1(x) or h2(x).
h1(x)
x
h2(x)

28. Dynamic perfect hashing
In Cuckoo hashing there is a single hash table but two hash functions: h1 and h2.
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
Each key in the table is either stored at position
h1(x) or h2(x).
h1(x) h2(x)
x

29. Dynamic perfect hashing
In Cuckoo hashing there is a single hash table but two hash functions: h1 and h2.
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
Each key in the table is either stored at position
h1(x) or h2(x).
h1(x)
x
h2(x)

30. Dynamic perfect hashing
In Cuckoo hashing there is a single hash table but two hash functions: h1 and h2.
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
Each key in the table is either stored at position
h1(x) or h2(x).
h1(x) h2(x)
x

31. Dynamic perfect hashing
In Cuckoo hashing there is a single hash table but two hash functions: h1 and h2.
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
Each key in the table is either stored at position
h1(x) or h2(x).
h1(x) h2(x)
x
Important: We never store multiple keys at the same position

32. Dynamic perfect hashing
In Cuckoo hashing there is a single hash table but two hash functions: h1 and h2.
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
Each key in the table is either stored at position
h1(x) or h2(x).
h1(x) h2(x)
x
Important: We never store multiple keys at the same position
Therefore, as claimed, lookup takes O(1) time. . .

33. Dynamic perfect hashing
In Cuckoo hashing there is a single hash table but two hash functions: h1 and h2.
A dynamic dictionary stores (key, value)-pairs and supports:
add(key, value), lookup(key) (which returns value) and delete(key)
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
Each key in the table is either stored at position
h1(x) or h2(x).
h1(x) h2(x)
x
Important: We never store multiple keys at the same position
Therefore, as claimed, lookup takes O(1) time. . . but how do we do inserts?

34. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
xx

35. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop (and congratulate yourself on a job well done)
x

36. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
x

37. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
xx

38. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
y
xx

39. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
y
xx

40. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
y
xx

41. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
y
x

42. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
where should we put key y?
y
x

43. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
where should we put key y?
in the other position it’s allowed in
y
x

44. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
where should we put key y?
in the other position it’s allowed in
y
x
h1(y) h2(y)

45. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
Step 3: Let pos be the other position y is allowed to be in
i.e pos = h2(y) if h1(x) = h1(y) and pos = h1(y) otherwise
y
x
h1(y) h2(y)

46. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
Step 3: Let pos be the other position y is allowed to be in
i.e pos = h2(y) if h1(x) = h1(y) and pos = h1(y) otherwise
Step 4: Attempt to put y in position pos
if that position is empty, stop
y
x
h1(y) h2(y)

47. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
Step 3: Let pos be the other position y is allowed to be in
i.e pos = h2(y) if h1(x) = h1(y) and pos = h1(y) otherwise
Step 4: Attempt to put y in position pos
if that position is empty, stop
h1(y) h2(y)
yx

48. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
Step 3: Let pos be the other position y is allowed to be in
i.e pos = h2(y) if h1(x) = h1(y) and pos = h1(y) otherwise
Step 4: Attempt to put y in position pos
if that position is empty, stop
z
y
x
h1(y) h2(y)
h1(z)h2(z)

49. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
Step 3: Let pos be the other position y is allowed to be in
i.e pos = h2(y) if h1(x) = h1(y) and pos = h1(y) otherwise
Step 4: Attempt to put y in position pos
if that position is empty, stop
Step 5: Let z be the key currently in position pos
evict key z and replace it with key y
z
y
x
h1(y) h2(y)
h1(z)h2(z)

50. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
Step 3: Let pos be the other position y is allowed to be in
i.e pos = h2(y) if h1(x) = h1(y) and pos = h1(y) otherwise
Step 4: Attempt to put y in position pos
if that position is empty, stop
Step 5: Let z be the key currently in position pos
evict key z and replace it with key y
h1(y) h2(y)
yx
z
h1(z)h2(z)

51. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
Step 3: Let pos be the other position y is allowed to be in
i.e pos = h2(y) if h1(x) = h1(y) and pos = h1(y) otherwise
Step 4: Attempt to put y in position pos
if that position is empty, stop
Step 5: Let z be the key currently in position pos
evict key z and replace it with key y
h1(y) h2(y)
yx
z
h1(z)h2(z)

52. Inserts in Cuckoo hashing
h1(x) h2(x)
Step 1: Attempt to put x in position h1(x)
if that position is empty, stop
Step 2: Let y be the key currently in position h1(x)
evict key y and replace it with key x
Step 3: Let pos be the other position y is allowed to be in
i.e pos = h2(y) if h1(x) = h1(y) and pos = h1(y) otherwise
Step 4: Attempt to put y in position pos
if that position is empty, stop
Step 5: Let z be the key currently in position pos
evict key z and replace it with key y and so on. . .
h1(y) h2(y)
yx
z
h1(z)h2(z)

53. Pseudocode
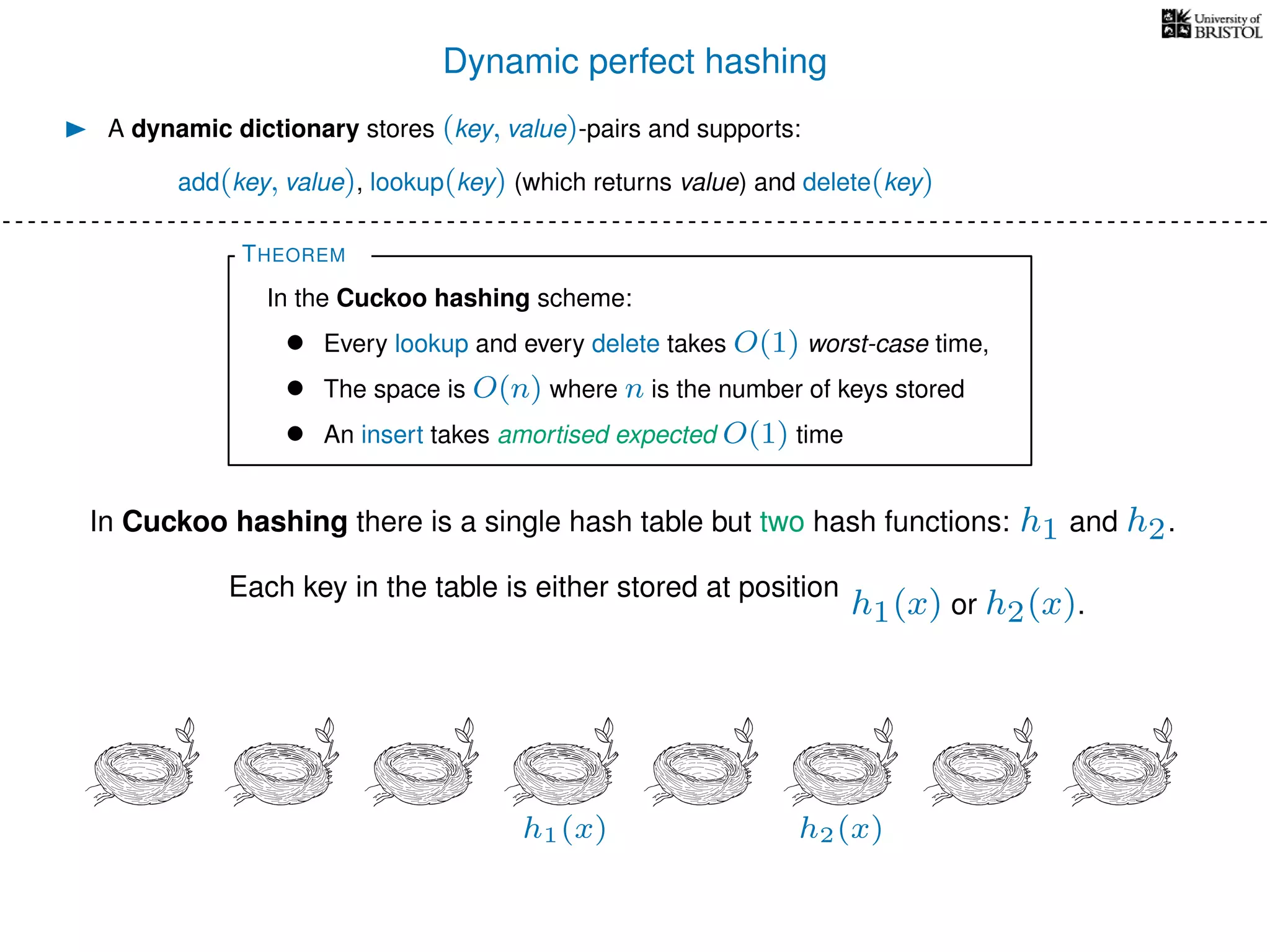
h1(x) h2(x)
h1(y) h2(y)
yx
z
h1(z)h2(z)
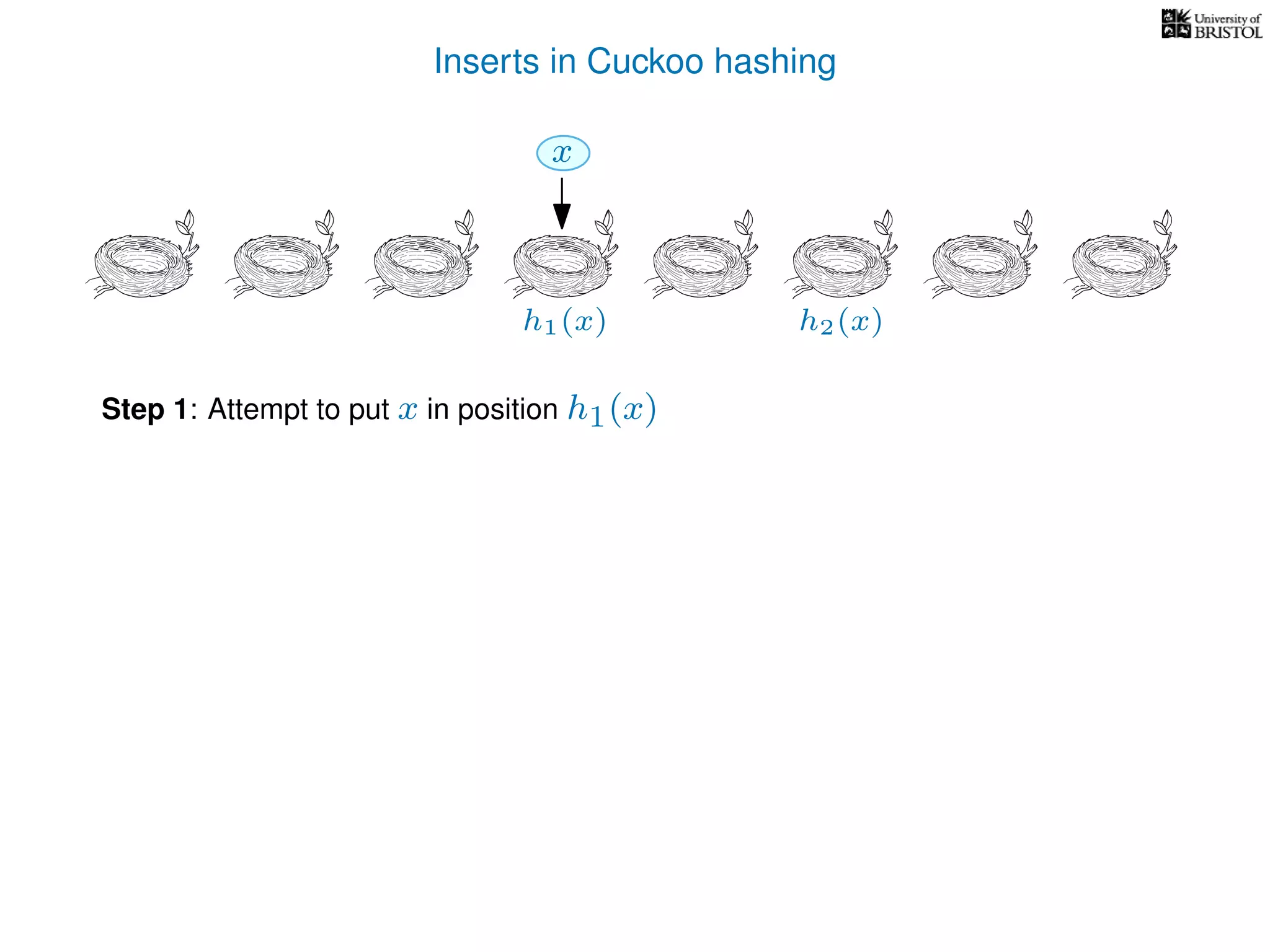
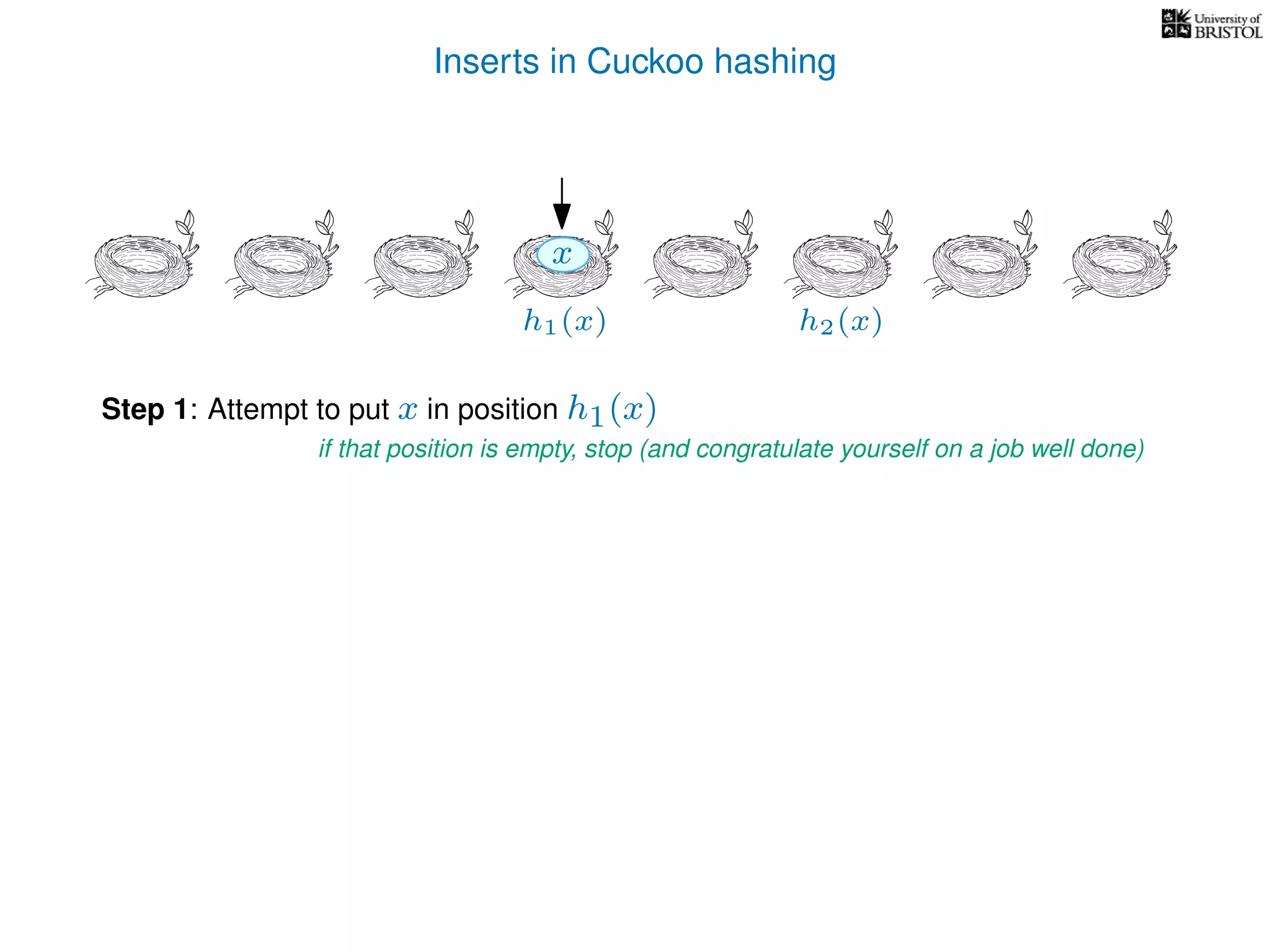
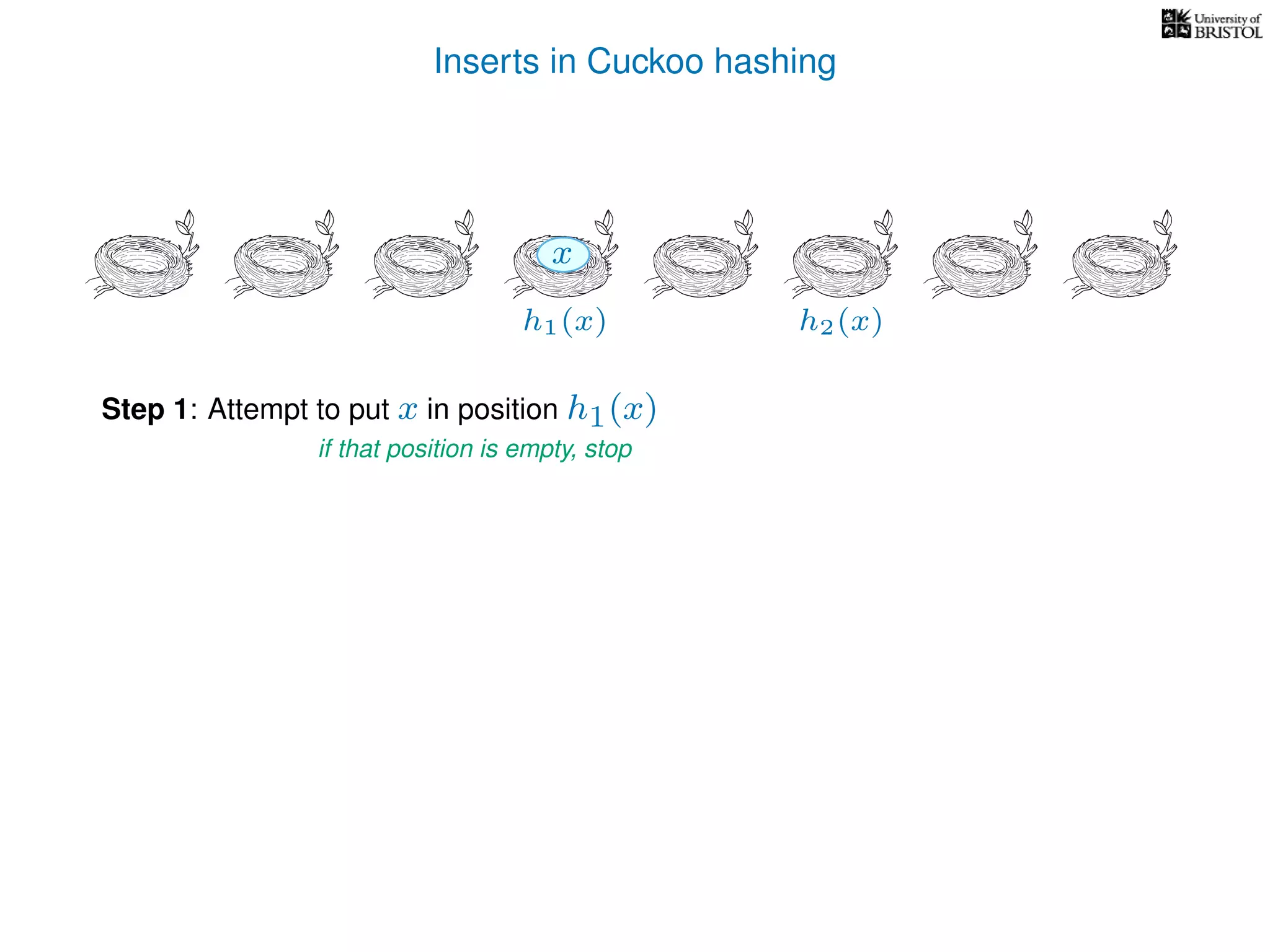
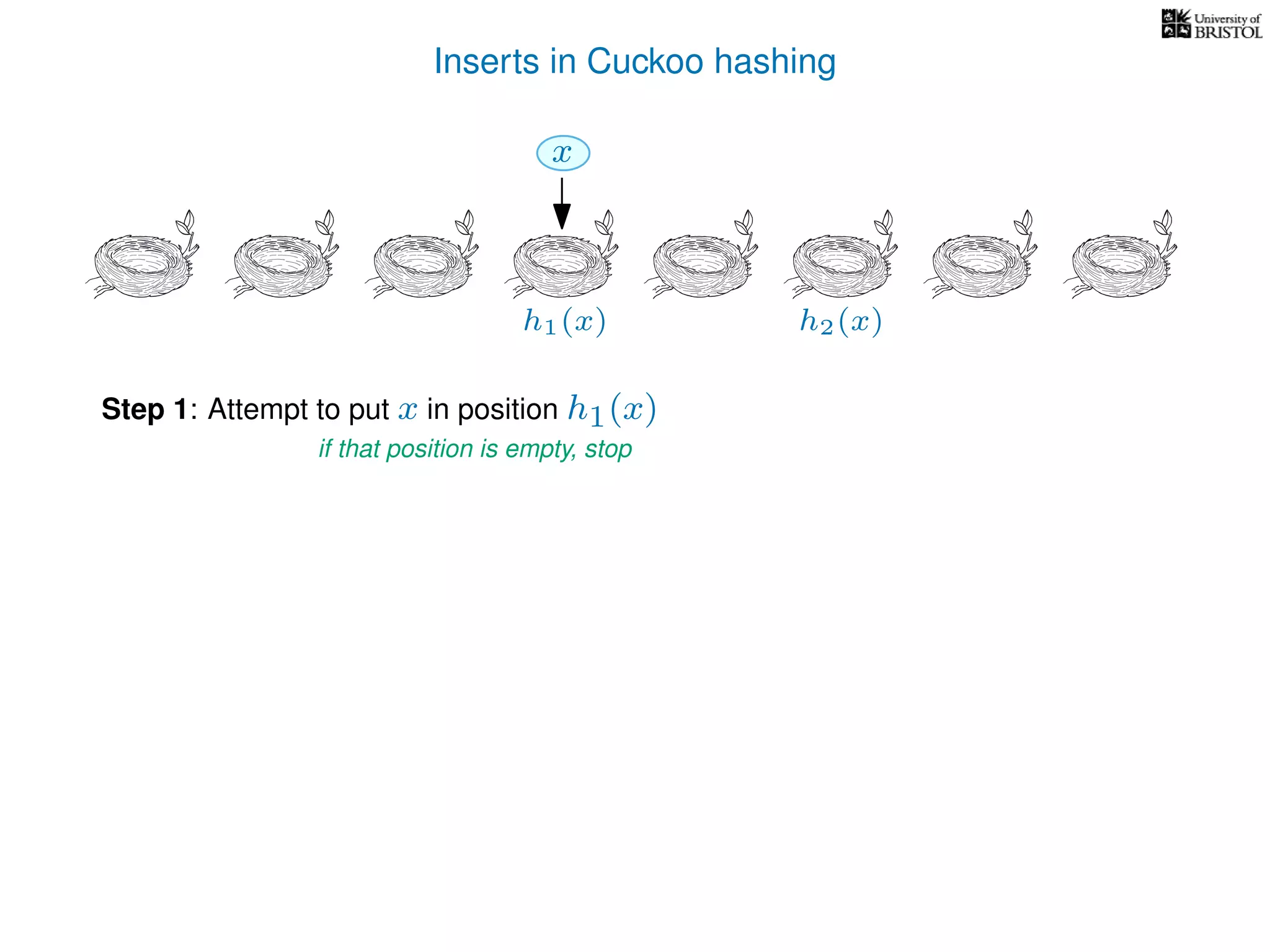
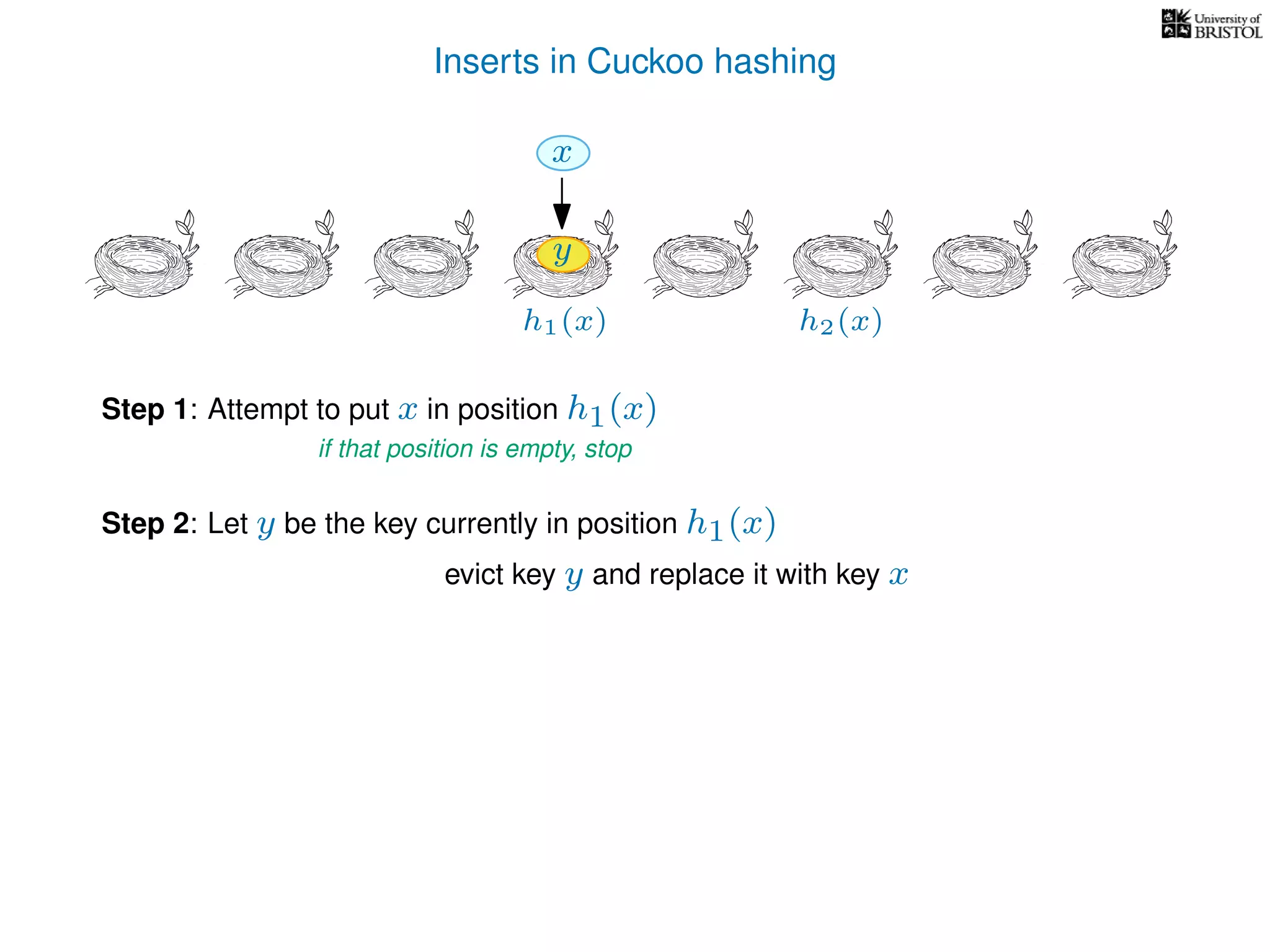
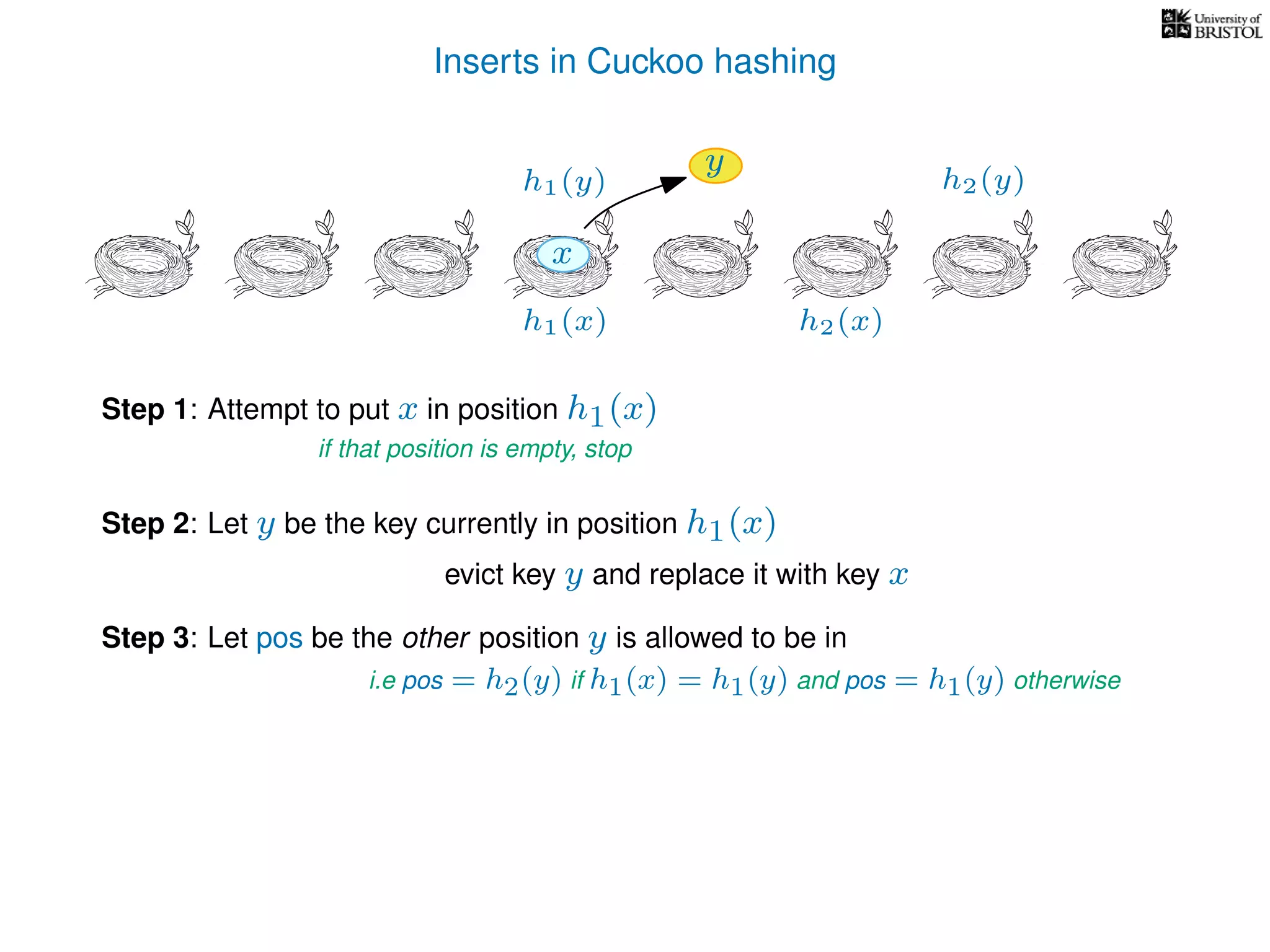
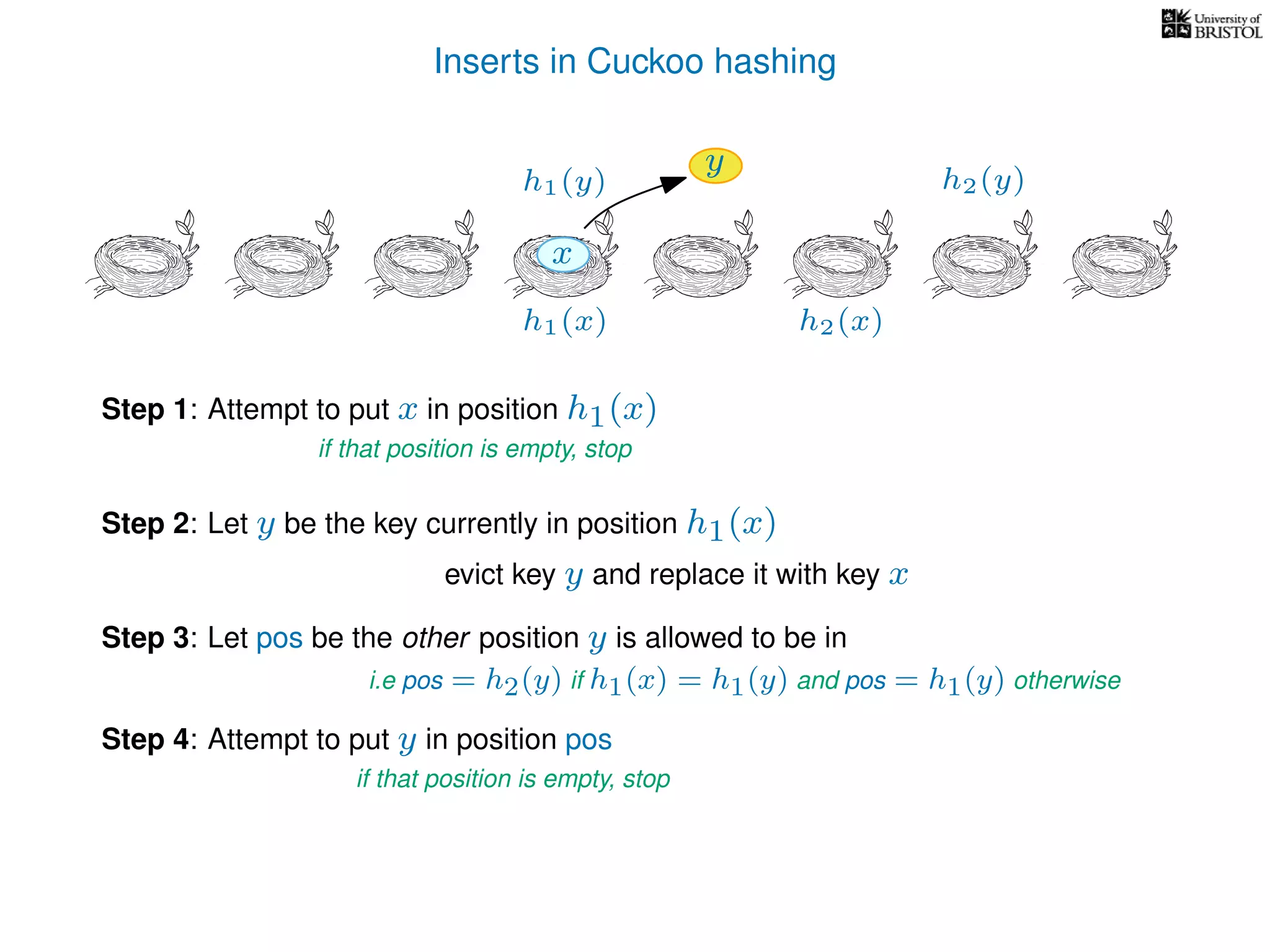
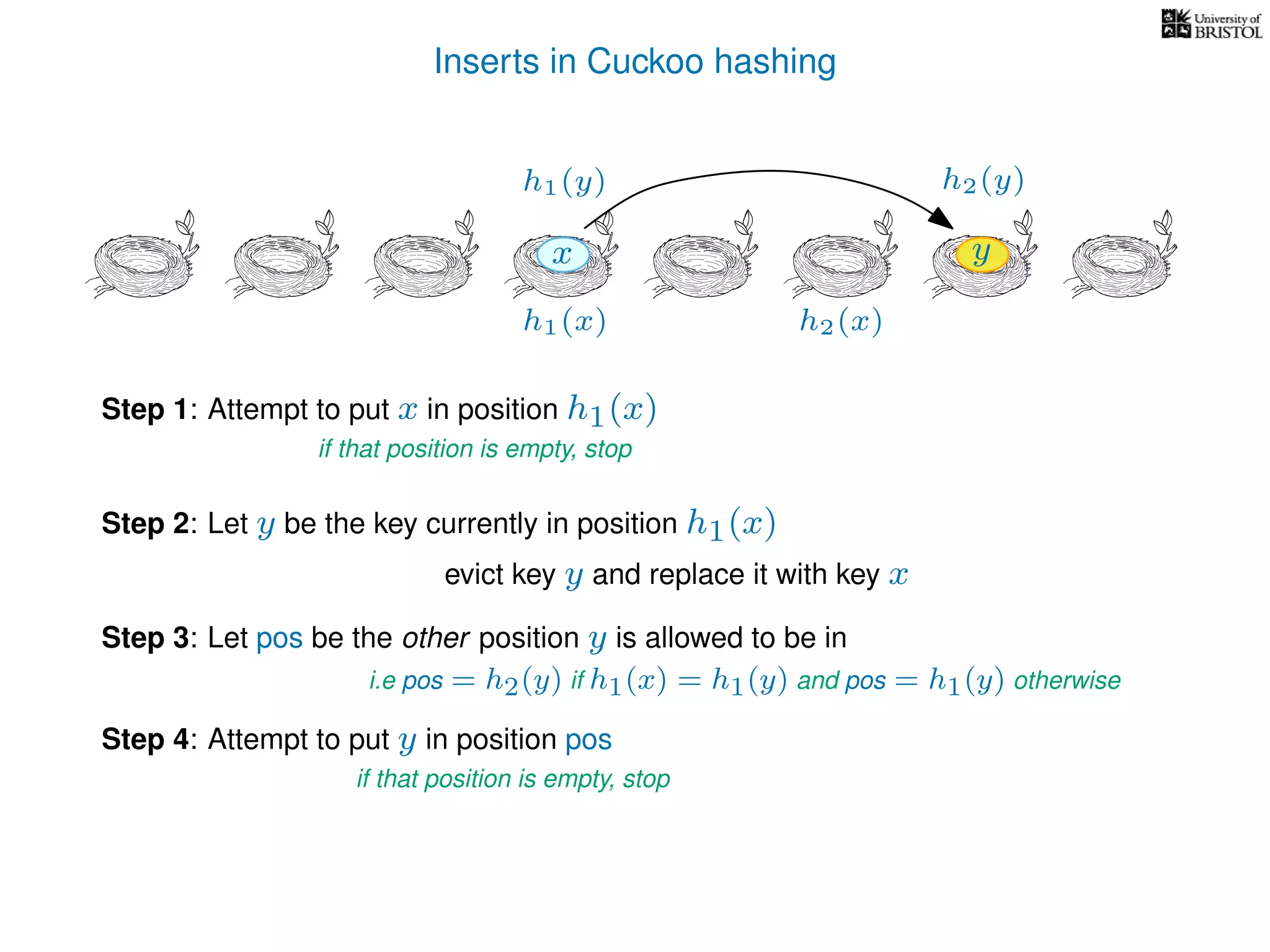
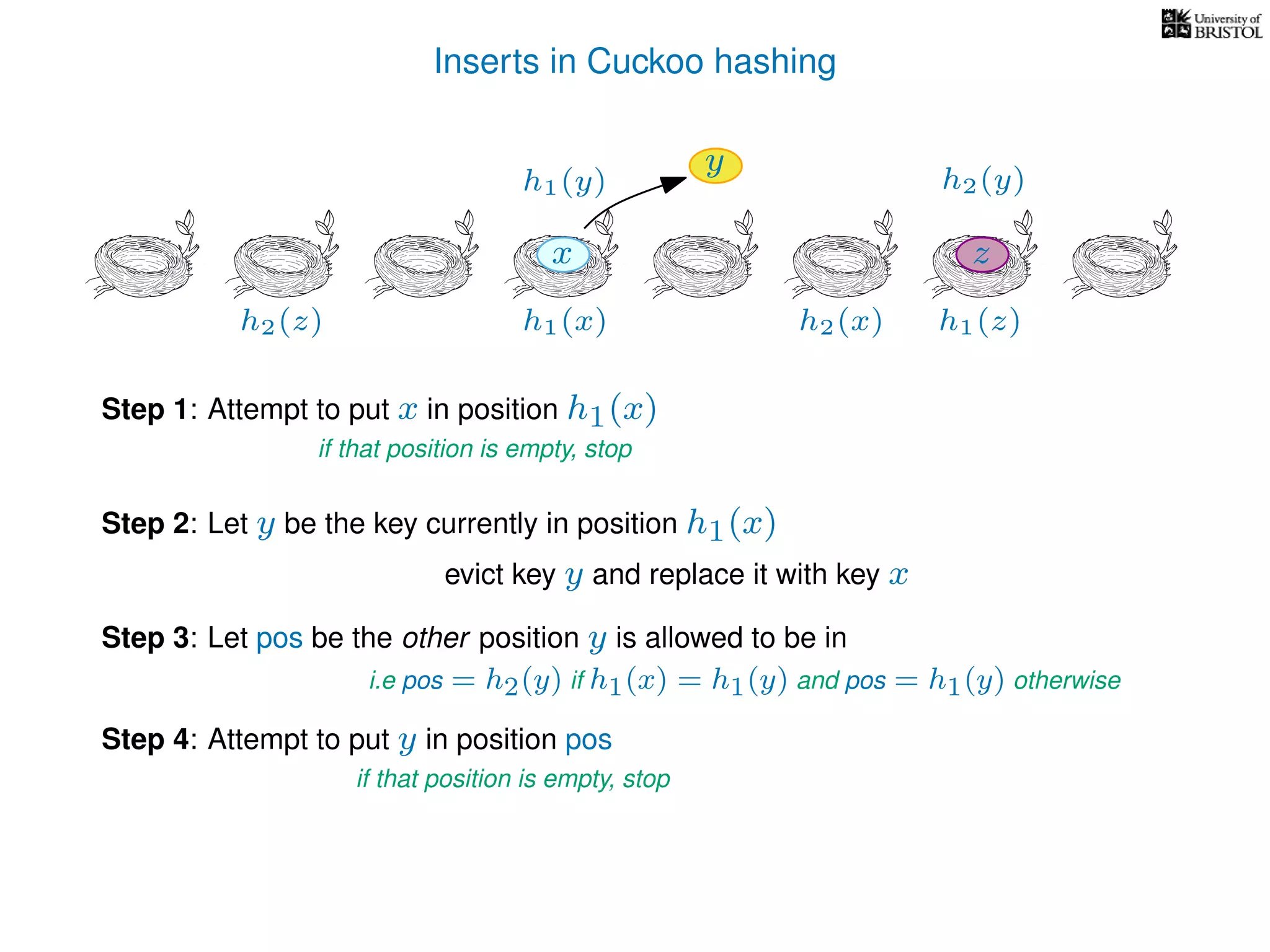
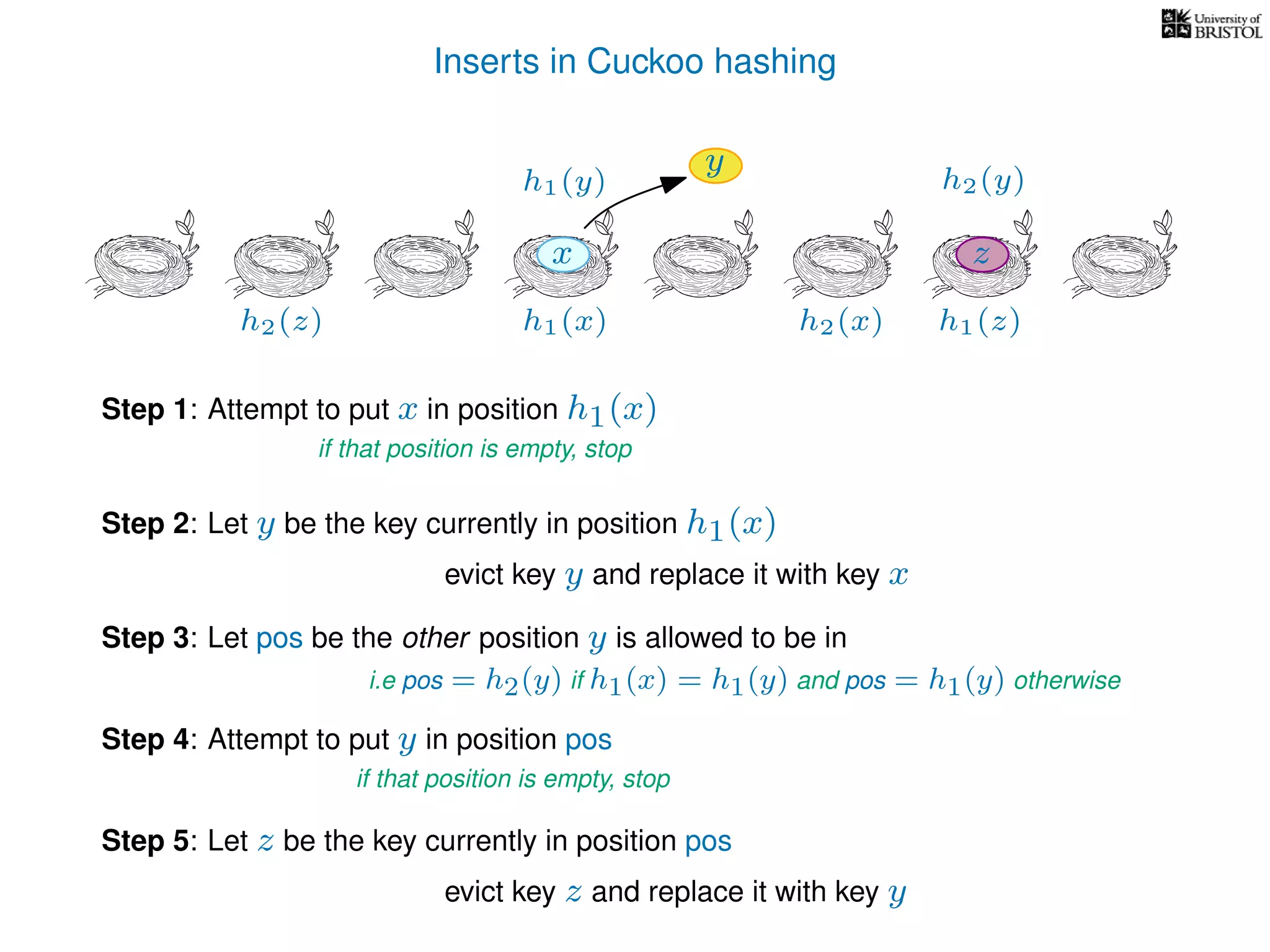
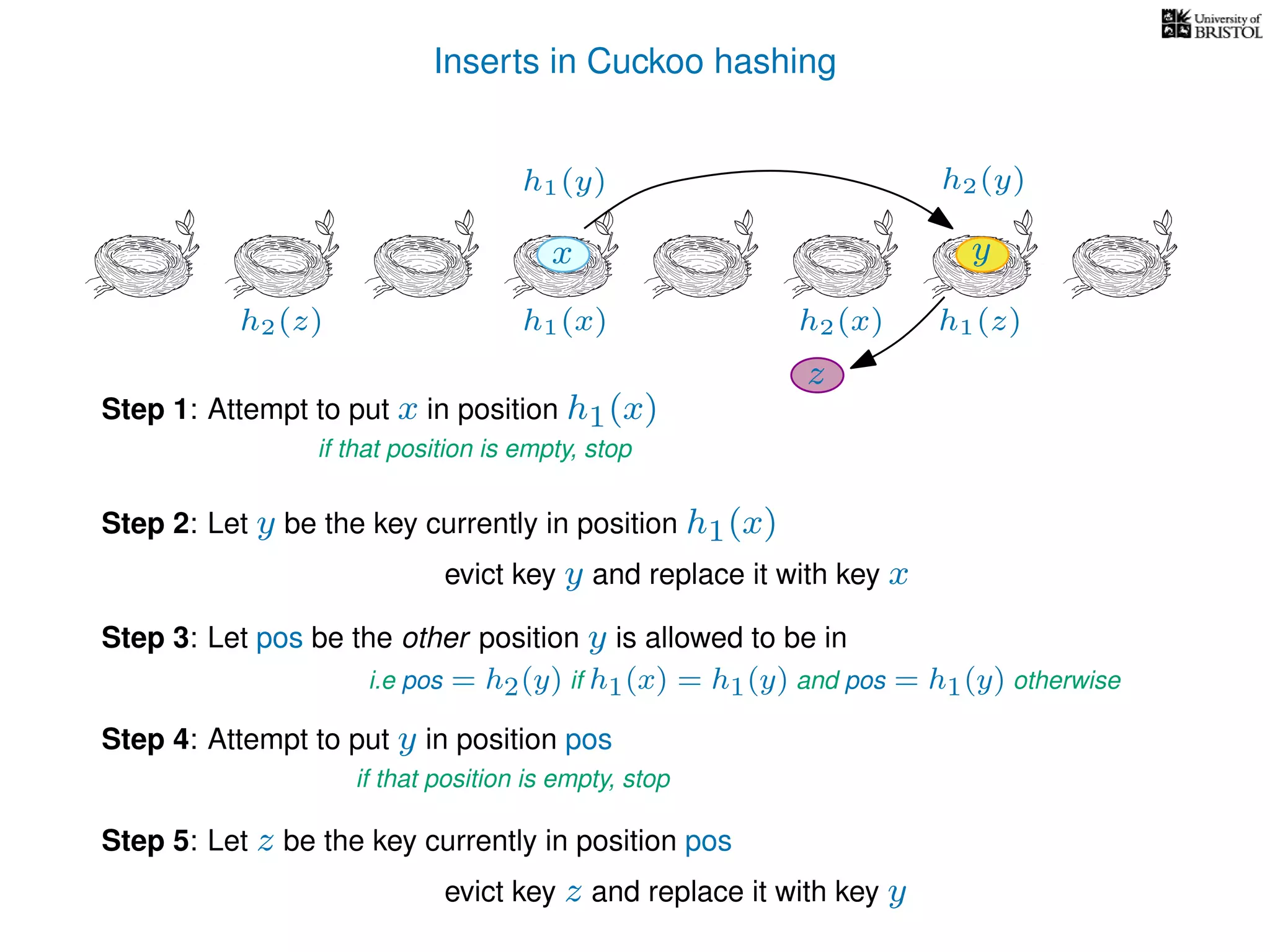
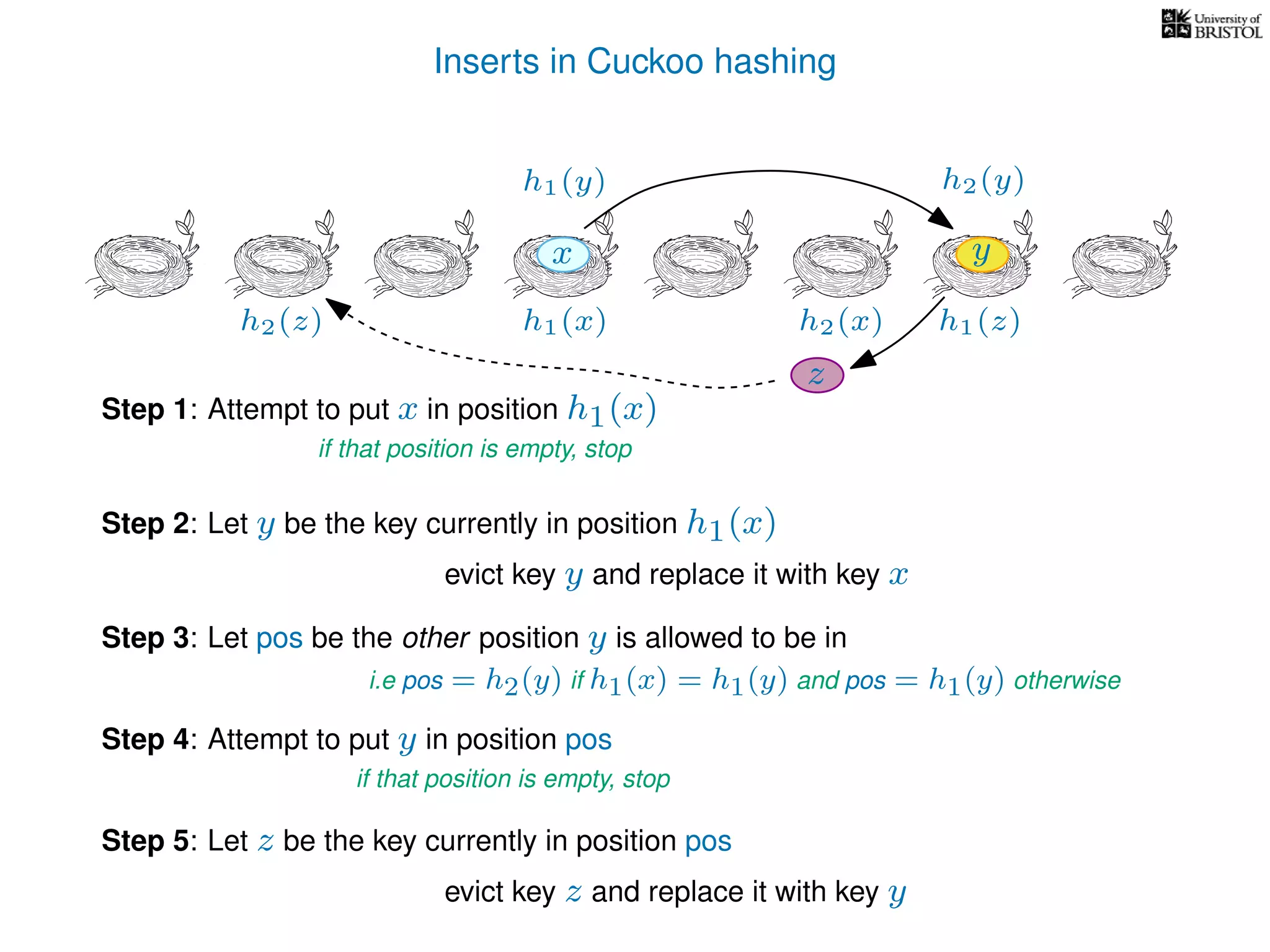
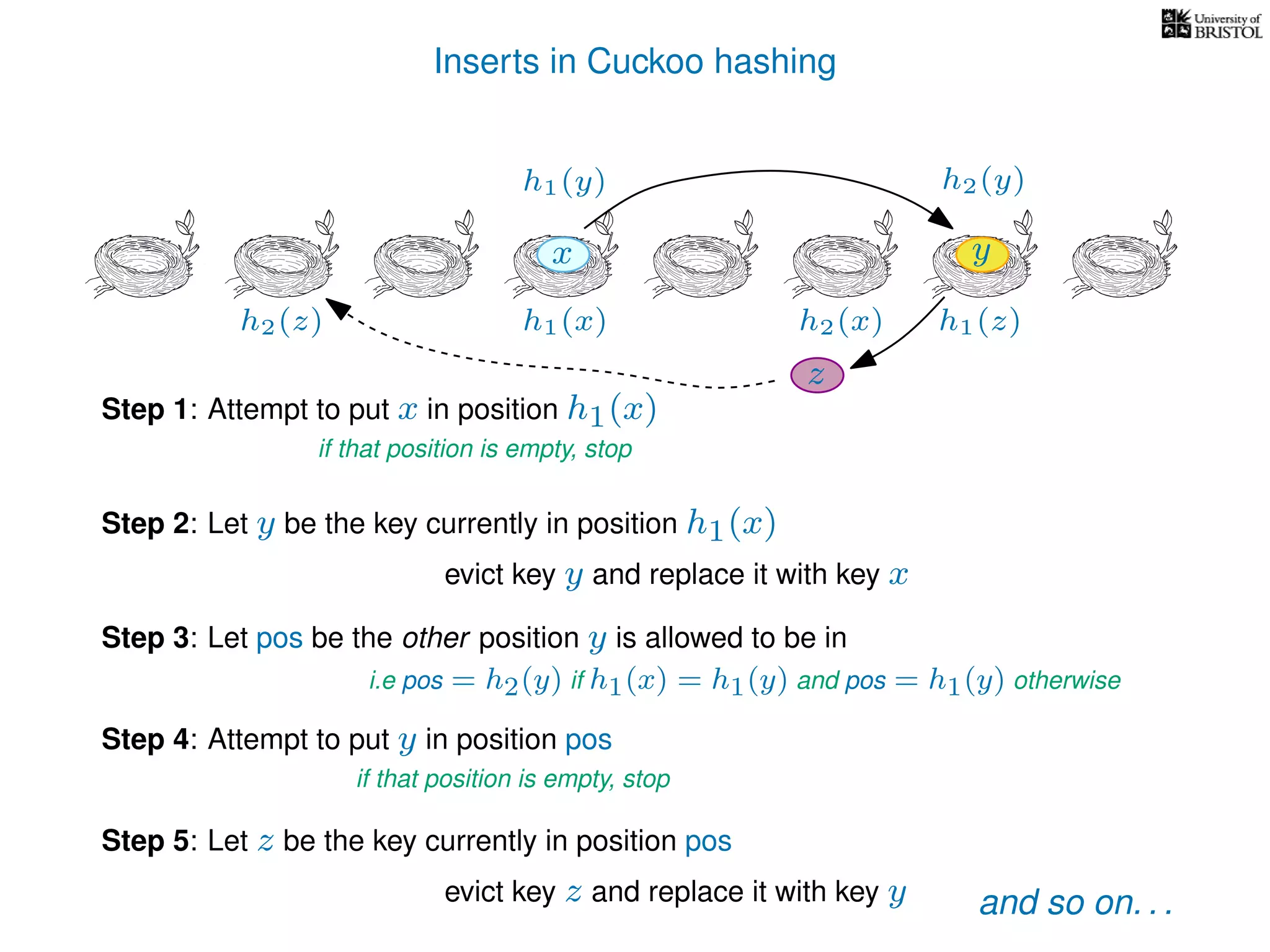
add(x):
pos ← h1(x)
Repeat at most n times:
If T[pos] is empty then T[pos] ← x.
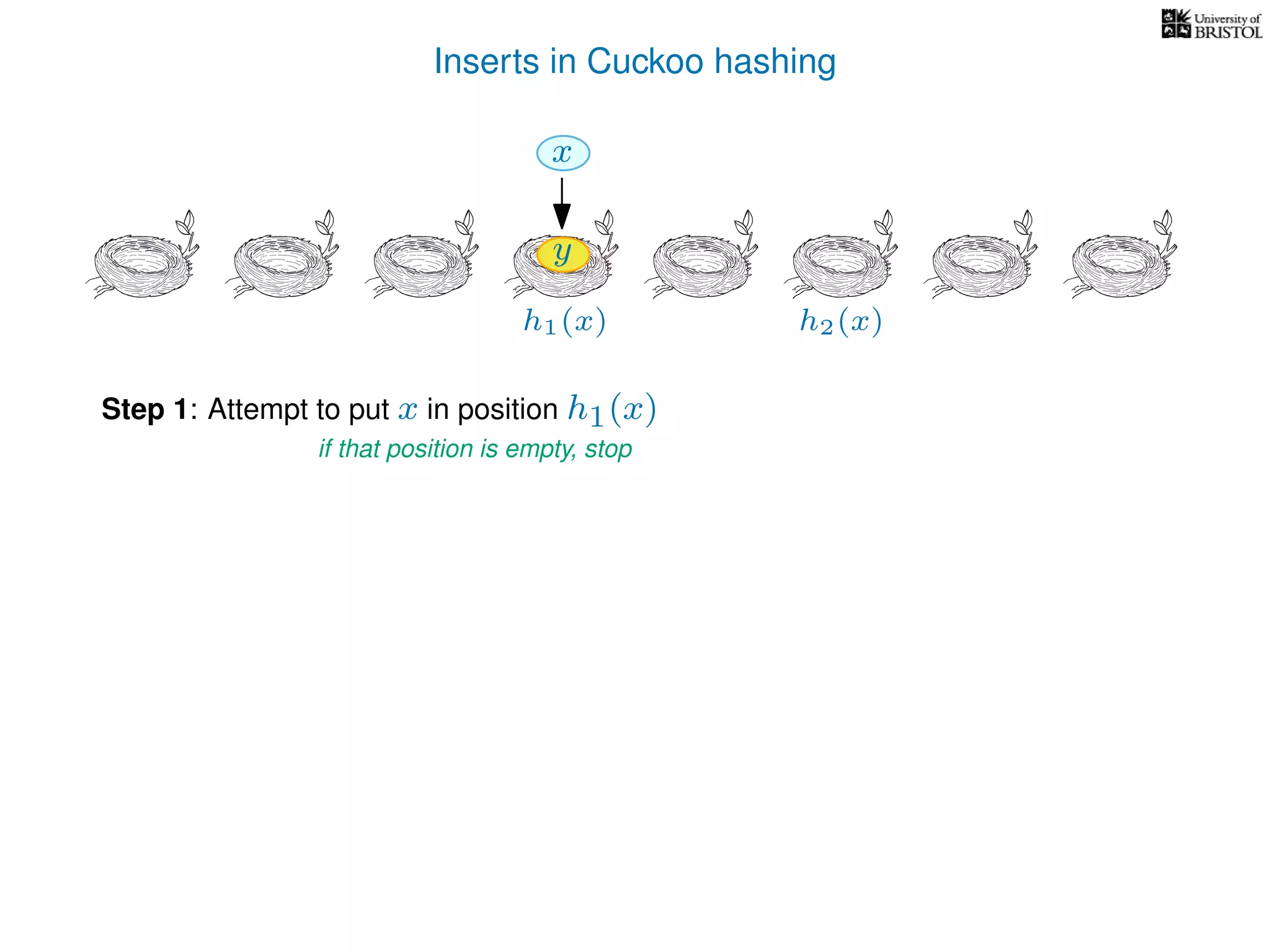
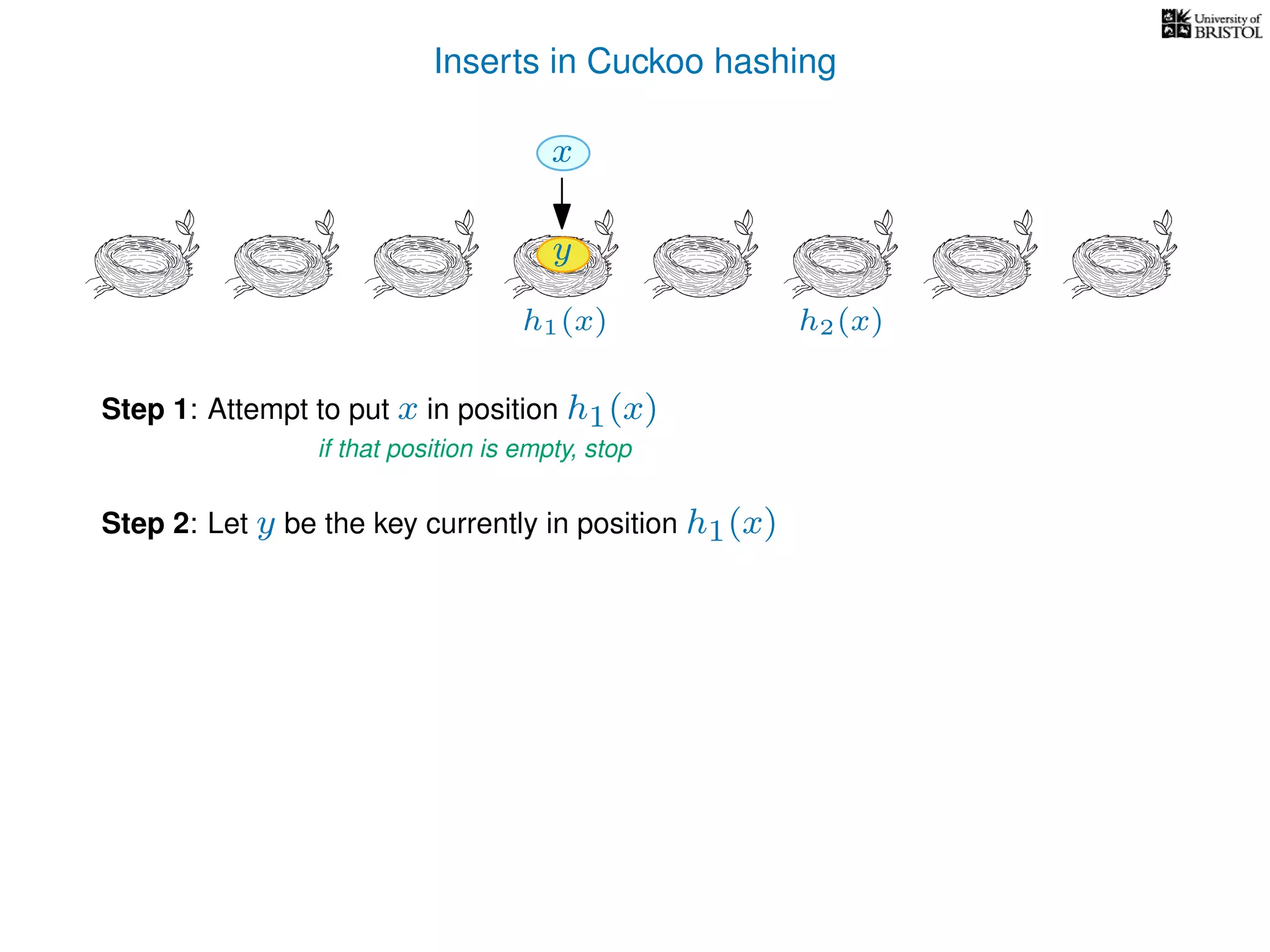
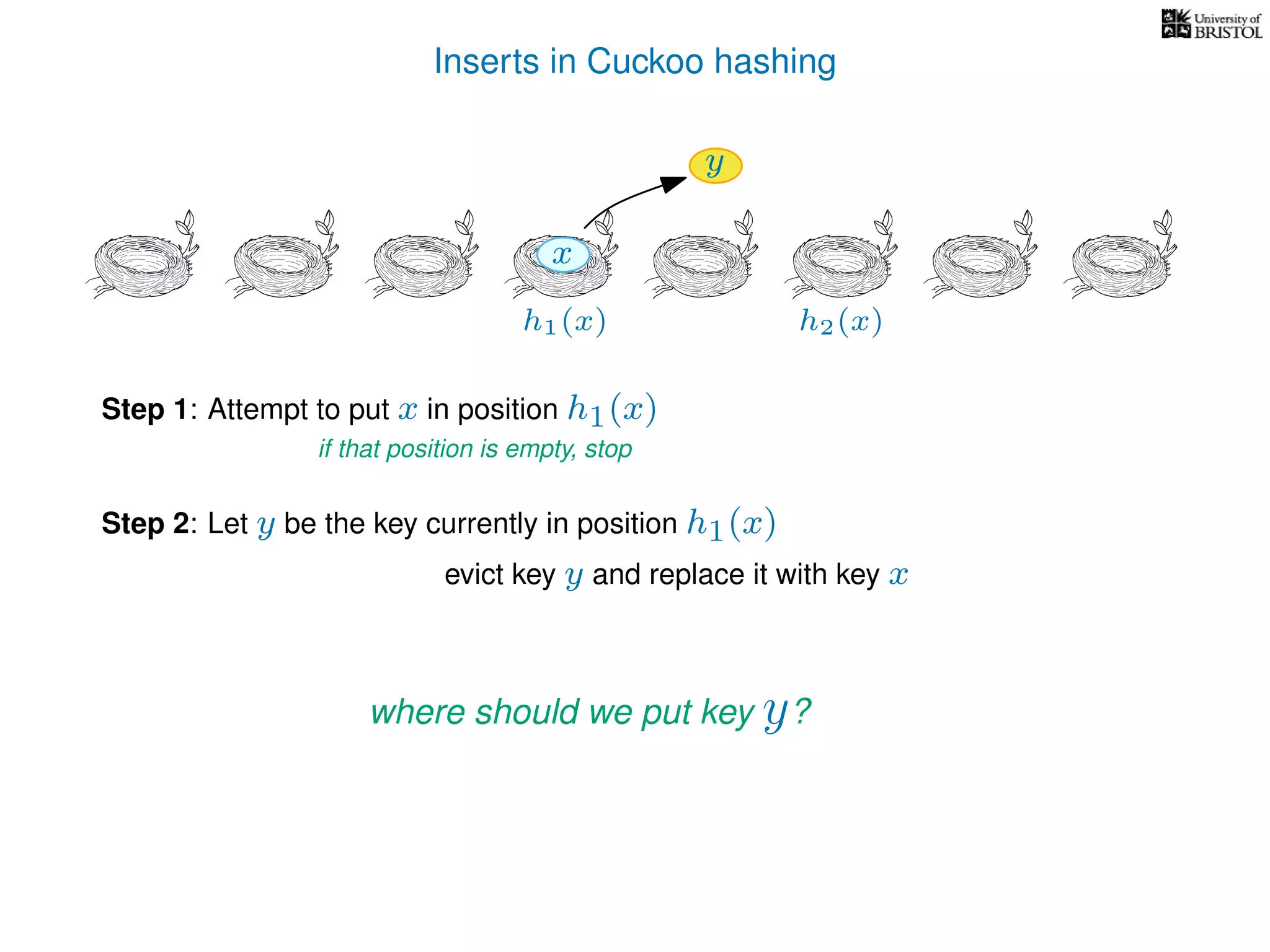
Otherwise,
y ← T[pos],
T[pos] ← x,
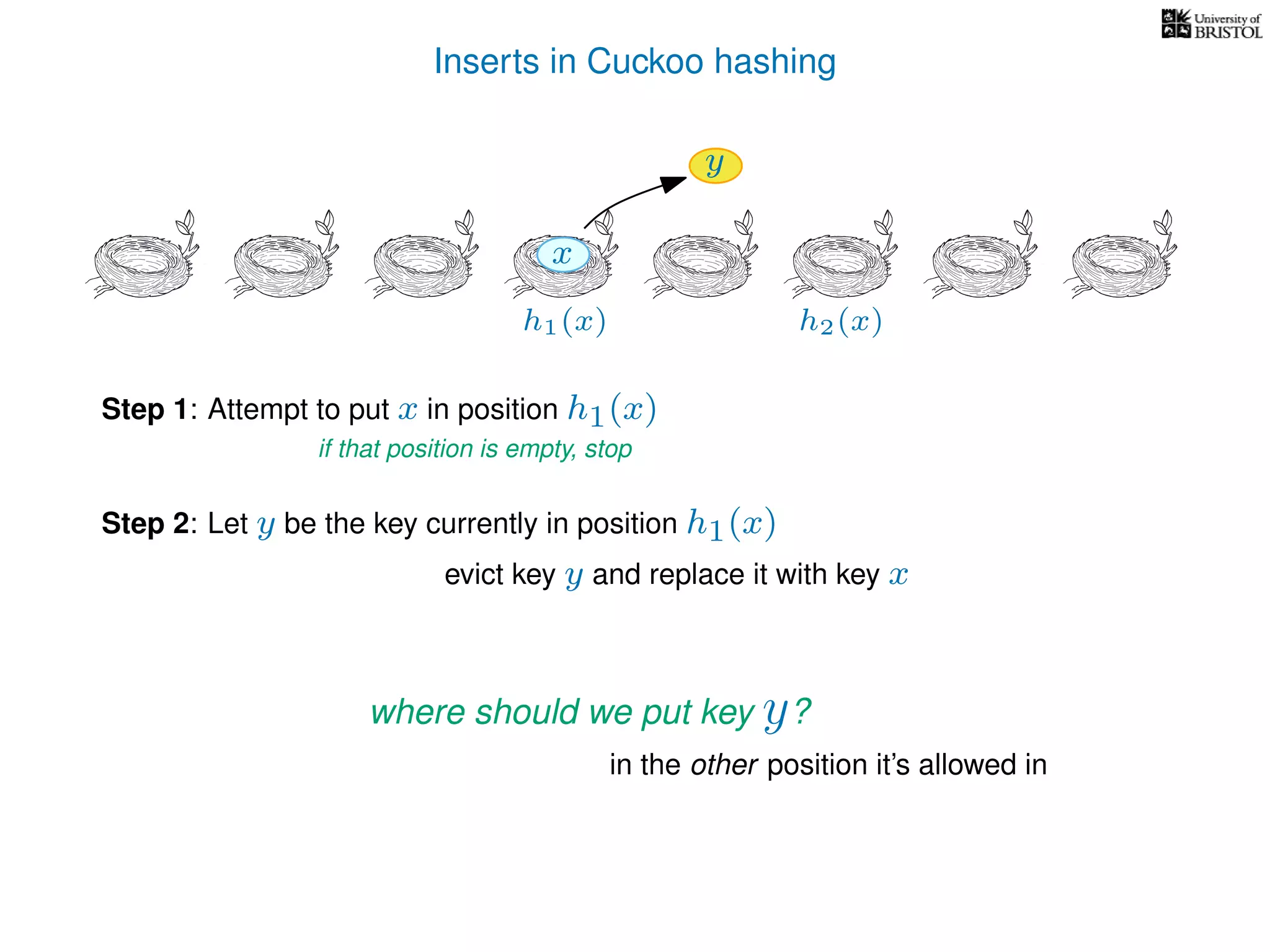
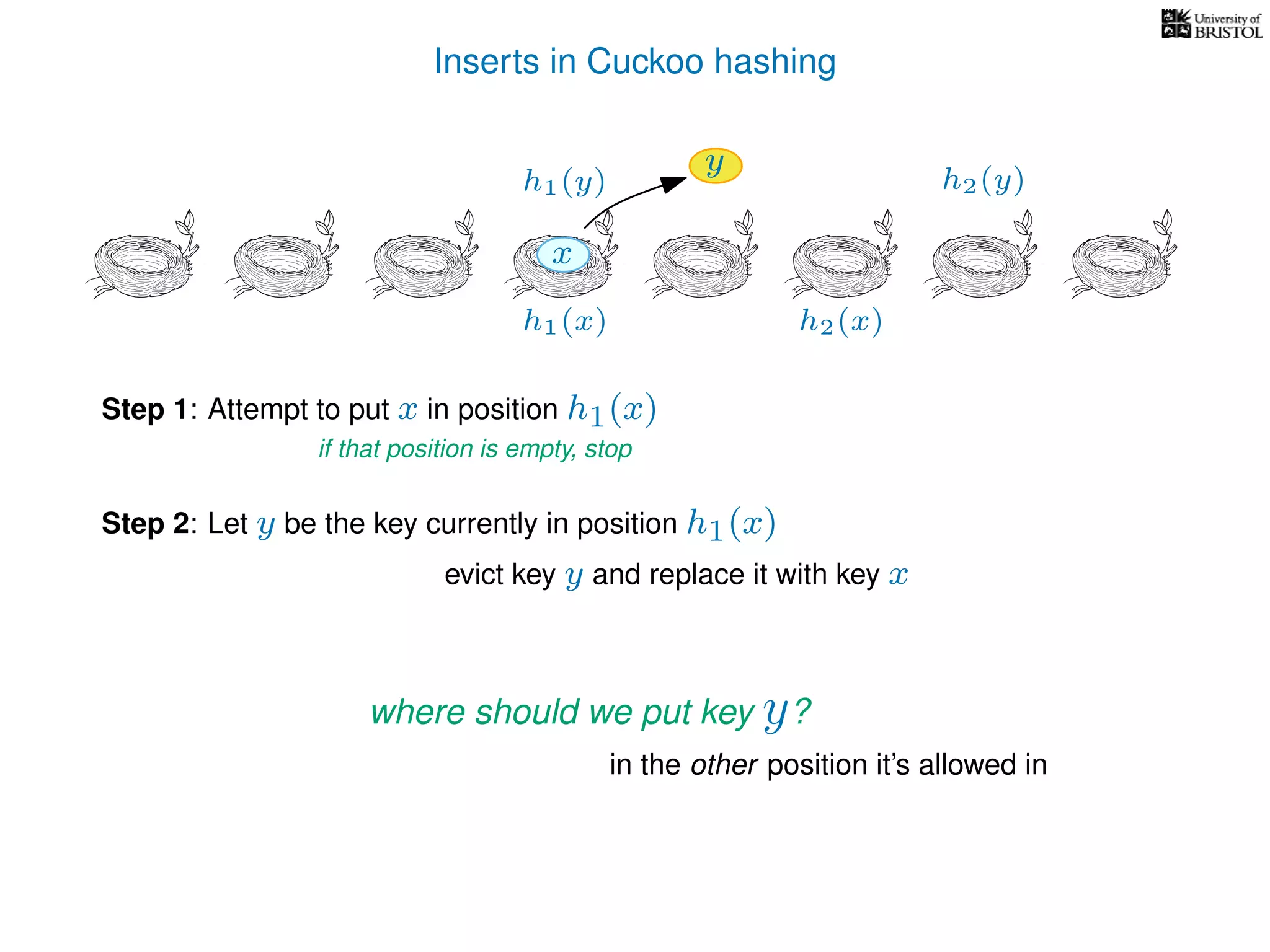
pos ← the other possible location for y.
(i.e. if y was evicted from h1(y) then pos ← h2(y), otherwise pos ← h1(y).)
x ← y.
Repeat
Give up and rehash the whole table.
i.e. empty the table, pick two new hash functions and reinsert every key

54. Rehashing
If we fail to insert a new key x,
(i.e. we still have an “evicted” key after moving around keys n times)
then we declare the table “rubbish” and rehash.

55. Rehashing
If we fail to insert a new key x,
(i.e. we still have an “evicted” key after moving around keys n times)
then we declare the table “rubbish” and rehash.
What does rehashing involve?

56. Rehashing
If we fail to insert a new key x,
(i.e. we still have an “evicted” key after moving around keys n times)
then we declare the table “rubbish” and rehash.
What does rehashing involve?
Suppose that the table contains the k keys x1, . . . , xk
at the time of we fail to insert key x.

57. Rehashing
If we fail to insert a new key x,
To rehash we:
(i.e. we still have an “evicted” key after moving around keys n times)
then we declare the table “rubbish” and rehash.
What does rehashing involve?
Suppose that the table contains the k keys x1, . . . , xk
at the time of we fail to insert key x.

58. Rehashing
If we fail to insert a new key x,
To rehash we:
(i.e. we still have an “evicted” key after moving around keys n times)
then we declare the table “rubbish” and rehash.
What does rehashing involve?
Suppose that the table contains the k keys x1, . . . , xk
at the time of we fail to insert key x.
Randomly pick two new hash functions h1 and h2. (More about this in a minute.)

59. Rehashing
If we fail to insert a new key x,
To rehash we:
(i.e. we still have an “evicted” key after moving around keys n times)
then we declare the table “rubbish” and rehash.
What does rehashing involve?
Suppose that the table contains the k keys x1, . . . , xk
at the time of we fail to insert key x.
Randomly pick two new hash functions h1 and h2. (More about this in a minute.)
Build a new empty hash table of the same size

60. Rehashing
If we fail to insert a new key x,
Reinsert the keys x1, . . . , xk and then x,
To rehash we:
(i.e. we still have an “evicted” key after moving around keys n times)
then we declare the table “rubbish” and rehash.
What does rehashing involve?
Suppose that the table contains the k keys x1, . . . , xk
at the time of we fail to insert key x.
Randomly pick two new hash functions h1 and h2. (More about this in a minute.)
Build a new empty hash table of the same size
one by one, using the normal add operation.

61. Rehashing
If we fail to insert a new key x,
Reinsert the keys x1, . . . , xk and then x,
To rehash we:
(i.e. we still have an “evicted” key after moving around keys n times)
then we declare the table “rubbish” and rehash.
What does rehashing involve?
Suppose that the table contains the k keys x1, . . . , xk
at the time of we fail to insert key x.
Randomly pick two new hash functions h1 and h2. (More about this in a minute.)
Build a new empty hash table of the same size
If we fail while rehashing. . . we start from the beginning again
one by one, using the normal add operation.

62. Rehashing
If we fail to insert a new key x,
Reinsert the keys x1, . . . , xk and then x,
To rehash we:
(i.e. we still have an “evicted” key after moving around keys n times)
then we declare the table “rubbish” and rehash.
What does rehashing involve?
Suppose that the table contains the k keys x1, . . . , xk
at the time of we fail to insert key x.
Randomly pick two new hash functions h1 and h2. (More about this in a minute.)
Build a new empty hash table of the same size
If we fail while rehashing. . . we start from the beginning again
This is rather slow. . . but we will prove that it happens rarely
one by one, using the normal add operation.

63. Assumptions
We will follow the analysis in the paper Cuckoo hashing for undergraduates,
2006, by Rasmus Pagh (see the link on unit web page).

64. Assumptions
We will follow the analysis in the paper Cuckoo hashing for undergraduates,
2006, by Rasmus Pagh (see the link on unit web page).
We make the following assumptions:

65. Assumptions
We will follow the analysis in the paper Cuckoo hashing for undergraduates,
2006, by Rasmus Pagh (see the link on unit web page).
We make the following assumptions:
h1 and h2 are independent
i.e. h1(x) says nothing about h2(x), and vice versa.

66. Assumptions
We will follow the analysis in the paper Cuckoo hashing for undergraduates,
2006, by Rasmus Pagh (see the link on unit web page).
We make the following assumptions:
h1 and h2 are truly random
i.e. each key is independently mapped to each of the m positions
in the hash table with probability 1
m .
h1 and h2 are independent
i.e. h1(x) says nothing about h2(x), and vice versa.

67. Assumptions
We will follow the analysis in the paper Cuckoo hashing for undergraduates,
2006, by Rasmus Pagh (see the link on unit web page).
We make the following assumptions:
h1 and h2 are truly random
Computing the value of h1(x) and h2(x) takes O(1) worst-case time
i.e. each key is independently mapped to each of the m positions
in the hash table with probability 1
m .
h1 and h2 are independent
i.e. h1(x) says nothing about h2(x), and vice versa.

68. Assumptions
We will follow the analysis in the paper Cuckoo hashing for undergraduates,
2006, by Rasmus Pagh (see the link on unit web page).
We make the following assumptions:
h1 and h2 are truly random
Computing the value of h1(x) and h2(x) takes O(1) worst-case time
i.e. each key is independently mapped to each of the m positions
in the hash table with probability 1
m .
h1 and h2 are independent
i.e. h1(x) says nothing about h2(x), and vice versa.
There are at most n keys in the hash table at any time.

69. Assumptions
We will follow the analysis in the paper Cuckoo hashing for undergraduates,
2006, by Rasmus Pagh (see the link on unit web page).
We make the following assumptions:
h1 and h2 are truly random
Computing the value of h1(x) and h2(x) takes O(1) worst-case time
i.e. each key is independently mapped to each of the m positions
in the hash table with probability 1
m .
h1 and h2 are independent
i.e. h1(x) says nothing about h2(x), and vice versa.
There are at most n keys in the hash table at any time.
REASONABLE
ASSUMPTION

70. Assumptions
We will follow the analysis in the paper Cuckoo hashing for undergraduates,
2006, by Rasmus Pagh (see the link on unit web page).
We make the following assumptions:
h1 and h2 are truly random
Computing the value of h1(x) and h2(x) takes O(1) worst-case time
i.e. each key is independently mapped to each of the m positions
in the hash table with probability 1
m .
h1 and h2 are independent
i.e. h1(x) says nothing about h2(x), and vice versa.
There are at most n keys in the hash table at any time.
UNREASONABLEASSUMPTION
REASONABLE
ASSUMPTION

71. Assumptions
We will follow the analysis in the paper Cuckoo hashing for undergraduates,
2006, by Rasmus Pagh (see the link on unit web page).
We make the following assumptions:
h1 and h2 are truly random
Computing the value of h1(x) and h2(x) takes O(1) worst-case time
i.e. each key is independently mapped to each of the m positions
in the hash table with probability 1
m .
h1 and h2 are independent
i.e. h1(x) says nothing about h2(x), and vice versa.
There are at most n keys in the hash table at any time.
UNREASONABLEASSUMPTION
REASONABLE
ASSUMPTION
QUESTIONABLE
ASSUMPTION

72. Assumptions
We will follow the analysis in the paper Cuckoo hashing for undergraduates,
2006, by Rasmus Pagh (see the link on unit web page).
We make the following assumptions:
h1 and h2 are truly random
Computing the value of h1(x) and h2(x) takes O(1) worst-case time
i.e. each key is independently mapped to each of the m positions
in the hash table with probability 1
m .
h1 and h2 are independent
i.e. h1(x) says nothing about h2(x), and vice versa.
There are at most n keys in the hash table at any time.
UNREASONABLEASSUMPTION
REASONABLE
ASSUMPTION
QUESTIONABLE
ASSUMPTION
NOT ACTUALLY ANASSUMPTION

73. Cuckoo graph
Hash table
(size m)

74. Cuckoo graph
Hash table
The cuckoo graph:(size m)

75. Cuckoo graph
Hash table
The cuckoo graph:(size m)
A vertex for each position of the table.

76. Cuckoo graph
Hash table
The cuckoo graph:
m vertices
(size m)
A vertex for each position of the table.

77. Cuckoo graph
Hash table
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).

78. Cuckoo graph
Hash table
x1
h2(x1)
h1(x1)
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).

79. Cuckoo graph
Hash table
x1
h2(x1)
h1(x1)
x2
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).

80. Cuckoo graph
Hash table
x1
h2(x1)
h1(x1)
x2
x3
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).

81. Cuckoo graph
Hash table
x1
h2(x1)
h1(x1)
x2
x3
x4
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).

82. Cuckoo graph
Hash table
x2
x3
x4
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x1

83. Cuckoo graph
Hash table
x2
x3
x4
x5
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x1

84. Cuckoo graph
Hash table
x2
x3
x4
x5
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
h1(x5)
x1
h2(x5)

85. Cuckoo graph
Hash table
x2
x3
x4
x5
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
h1(x5)
x1
h2(x5)
There is no space for x5. . .

86. Cuckoo graph
Hash table
x2
x3
x4
x5
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
h1(x5)
x1
h2(x5)
There is no space for x5. . .
so we make space
by moving x2 and then x3

87. Cuckoo graph
Hash table
x2
x3
x4
x5
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
h1(x5)
x1
h2(x5)
There is no space for x5. . .
so we make space
by moving x2 and then x3

88. Cuckoo graph
Hash table
x2
x3
x4
x5
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
h1(x5)
x1
h2(x5)
There is no space for x5. . .
so we make space
by moving x2 and then x3

89. Cuckoo graph
Hash table
x2
x4
x5
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x3
h1(x5)
x1
h2(x5)
There is no space for x5. . .
so we make space
by moving x2 and then x3

90. Cuckoo graph
Hash table
x2
x4
x5
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x3
h1(x5)
x1
h2(x5)
There is no space for x5. . .
so we make space
by moving x2 and then x3
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph

91. Cuckoo graph
Hash table
x2
x4
x5
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x3
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph

92. Cuckoo graph
Hash table
x2
x4
x5
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x3
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph

93. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x3
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph

94. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
Inserting key x6 creates a cycle.
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x3
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph

95. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
Inserting key x6 creates a cycle.
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
Cycles are dangerous. . .
x3
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph

96. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
Inserting key x6 creates a cycle.
x7
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
Cycles are dangerous. . .
x3
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph

97. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
Inserting key x6 creates a cycle.
x7
When key x7 is inserted where does it go?
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
Cycles are dangerous. . .
x3
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph

98. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
Inserting key x6 creates a cycle.
x7
When key x7 is inserted where does it go?
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
Cycles are dangerous. . .
x3
x1
there are 6 keys but only 5 spaces
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph

99. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
Inserting key x6 creates a cycle.
x7
When key x7 is inserted where does it go?
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
Cycles are dangerous. . .
The keys would be moved around in an infinite loop
x3
but we stop and rehash after n moves. . .
x1
there are 6 keys but only 5 spaces
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph

100. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
Inserting key x6 creates a cycle.
x7
When key x7 is inserted where does it go?
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
Cycles are dangerous. . .
The keys would be moved around in an infinite loop
x3
but we stop and rehash after n moves. . .
x1
there are 6 keys but only 5 spaces
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph
Inserting a key into a cycle always causes a rehash

101. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
x7
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x3
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph
Inserting a key into a cycle always causes a rehash

102. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
x7
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x3
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph
Inserting a key into a cycle always causes a rehash

103. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
x7
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x3
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph
Inserting a key into a cycle always causes a rehash
This is the only way a rehash can happen

104. Cuckoo graph
Hash table
x2
x4
x5
x6
The cuckoo graph:
For each key x there is an undirected edge
m vertices
x7
We will analyse the probability of either a cycle or a long path occuring in the graph
(size m)
A vertex for each position of the table.
between h1(x) and h2(x).
x3
while inserting any n keys.
x1
The number of moves performed while adding a key is
the length of the corresponding path in the cuckoo graph
Inserting a key into a cycle always causes a rehash
This is the only way a rehash can happen

105. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys

106. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?

107. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)

108. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
i j

109. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
i j
Probability of a shortest path of length 1 is at most
1
2·m

110. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
i j
Probability of a shortest path of length 2 is at most
1
4·m

111. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
i j
Probability of a shortest path of length 3 is at most
1
8·m

112. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
i j
Probability of a shortest path of length 4 is at most
1
16·m

113. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
i j
Probability of a shortest path of length 4 is at most
1
16·m
How likely is it that there even is a path?

114. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
How likely is it that there even is a path?

115. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
How likely is it that there even is a path?

116. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
How likely is it that there even is a path?
If a path exists from i to j, there must be a shortest path (from i to j)

117. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
How likely is it that there even is a path?
If a path exists from i to j, there must be a shortest path (from i to j)
Therefore the probability of a path from i to j existing is at most. . .
∞
=1
1
c ·m
(using the union bound over all possible path lengths.)

118. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
How likely is it that there even is a path?
If a path exists from i to j, there must be a shortest path (from i to j)
Therefore the probability of a path from i to j existing is at most. . .
∞
=1
1
c ·m
(using the union bound over all possible path lengths.)
= 1
m
∞
=1
1
c

119. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
How likely is it that there even is a path?
If a path exists from i to j, there must be a shortest path (from i to j)
Therefore the probability of a path from i to j existing is at most. . .
∞
=1
1
c ·m
(using the union bound over all possible path lengths.)
= 1
m
∞
=1
1
c
= 1
m·(c−1)
= 1
m

120. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What does this say?
(let c = 2 for simplicity)
How likely is it that there even is a path?
If a path exists from i to j, there must be a shortest path (from i to j)
Therefore the probability of a path from i to j existing is at most. . .
∞
=1
1
c ·m
(using the union bound over all possible path lengths.)
= 1
m
∞
=1
1
c
= 1
m·(c−1)
= 1
m
So a path from i to j is rather unlikely to exist

121. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What is the proof?

122. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What is the proof?
The proof is in the directors cut of the slides (on blackboard)

123. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What is the proof?
The proof is in the directors cut of the slides (on blackboard)
Can we at least see the pictures?

124. Paths in the cuckoo graph
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
table size is m n keys
What is the proof?
The proof is in the directors cut of the slides (on blackboard)
Can we at least see the pictures?
The proof is by induction on the length :
Base case: = 1.
i j
key x
ki j
−1
Inductive step:
Argue that each key has prob 2
m2 to
create an edge (i, j)
Union bound over all n keys
Pick a third point k to split the path
very very unlikely
very
unlikely
Union bound over all k then all keys

125. Back to the start (again) (again)
A dynamic dictionary stores (key, value)-pairs and supports:
Universe U of u keys.
Hash table T of size m n.
Collisions are fixed by chaining
n arbitrary operations arrive online, one at a time.
add(key, value), lookup(key) (which returns value) and delete(key)
bucketing
We require that we can recover
any key from its bucket in O(s) time
where s is the number of keys in the bucket
If our construction has the property that,
for any two keys x, y ∈ U (with x = y),
the probability that x and y are in the same bucket is O 1
m
For any n operations, the expected run-time is O(1) per operation.
Locating the bucket containing
a given key takes O(1) time
table size is m n keys

126. Don’t put all your eggs in one bucket
Hash table
We say that two keys x, y are in the same bucket (conceptually)
x
y
z
w
iff there is a path between h1(x) and h1(y)
in the cuckoo graph.
table size is m n keys

127. Don’t put all your eggs in one bucket
Hash table
We say that two keys x, y are in the same bucket (conceptually)
For two distinct keys x, y, the probability
∞
=1
4
c · m
=
4
m
·
∞
=1
1
c
=
4
m(c − 1)
= O
1
m
x
y
z
where c > 1 is a constant.
w
iff there is a path between h1(x) and h1(y)
in the cuckoo graph.
that they are in the same bucket is at most
(another union bound over all possible path lengths.)
table size is m n keys

128. Don’t put all your eggs in one bucket
Hash table
We say that two keys x, y are in the same bucket (conceptually)
For two distinct keys x, y, the probability
∞
=1
4
c · m
=
4
m
·
∞
=1
1
c
=
4
m(c − 1)
= O
1
m
x
y
z
where c > 1 is a constant.
w
iff there is a path between h1(x) and h1(y)
in the cuckoo graph.
that they are in the same bucket is at most
(another union bound over all possible path lengths.)
table size is m n keys
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA

129. Don’t put all your eggs in one bucket
Hash table
We say that two keys x, y are in the same bucket (conceptually)
For two distinct keys x, y, the probability
∞
=1
4
c · m
=
4
m
·
∞
=1
1
c
=
4
m(c − 1)
= O
1
m
x
y
z
where c > 1 is a constant.
w
iff there is a path between h1(x) and h1(y)
in the cuckoo graph.
that they are in the same bucket is at most
(another union bound over all possible path lengths.)
table size is m n keys

130. Don’t put all your eggs in one bucket
Hash table
We say that two keys x, y are in the same bucket (conceptually)
For two distinct keys x, y, the probability
∞
=1
4
c · m
=
4
m
·
∞
=1
1
c
=
4
m(c − 1)
= O
1
m
x
y
z
where c > 1 is a constant.
The time for an operation on x is bounded byw
iff there is a path between h1(x) and h1(y)
in the cuckoo graph.
that they are in the same bucket is at most
(another union bound over all possible path lengths.)
the number of items in the bucket. (assuming there are no cycles.)
table size is m n keys

131. Don’t put all your eggs in one bucket
Hash table
We say that two keys x, y are in the same bucket (conceptually)
For two distinct keys x, y, the probability
∞
=1
4
c · m
=
4
m
·
∞
=1
1
c
=
4
m(c − 1)
= O
1
m
x
y
z
where c > 1 is a constant.
The time for an operation on x is bounded byw
So we have that the expected time per operation is O(1)
iff there is a path between h1(x) and h1(y)
in the cuckoo graph.
that they are in the same bucket is at most
(another union bound over all possible path lengths.)
the number of items in the bucket. (assuming there are no cycles.)
(assuming that m 2cn and there are no cycles).
table size is m n keys

132. Don’t put all your eggs in one bucket
Hash table
We say that two keys x, y are in the same bucket (conceptually)
For two distinct keys x, y, the probability
∞
=1
4
c · m
=
4
m
·
∞
=1
1
c
=
4
m(c − 1)
= O
1
m
x
y
z
where c > 1 is a constant.
The time for an operation on x is bounded byw
So we have that the expected time per operation is O(1)
iff there is a path between h1(x) and h1(y)
in the cuckoo graph.
that they are in the same bucket is at most
(another union bound over all possible path lengths.)
the number of items in the bucket. (assuming there are no cycles.)
Further, lookups take O(1) time in the worst case.
(assuming that m 2cn and there are no cycles).
table size is m n keys

133. Rehashing
The previous analysis on the expected running time holds when there are no cycles.

134. Rehashing
The previous analysis on the expected running time holds when there are no cycles.
However, we would expect there to be cycles every now and then, causing a rehash.

135. Rehashing
The previous analysis on the expected running time holds when there are no cycles.
However, we would expect there to be cycles every now and then, causing a rehash.
How often does this happen? (sketch proof)

136. Rehashing
The previous analysis on the expected running time holds when there are no cycles.
However, we would expect there to be cycles every now and then, causing a rehash.
How often does this happen? (sketch proof)
Consider inserting n keys into the table. . .

137. Rehashing
The previous analysis on the expected running time holds when there are no cycles.
However, we would expect there to be cycles every now and then, causing a rehash.
A cycle is a path from a vertex i back to itself.
How often does this happen? (sketch proof)
Consider inserting n keys into the table. . . i

138. Rehashing
The previous analysis on the expected running time holds when there are no cycles.
However, we would expect there to be cycles every now and then, causing a rehash.
A cycle is a path from a vertex i back to itself.
How often does this happen? (sketch proof)
Consider inserting n keys into the table. . .
so use previous result with i = j.. . .
i

139. Rehashing
The previous analysis on the expected running time holds when there are no cycles.
However, we would expect there to be cycles every now and then, causing a rehash.
A cycle is a path from a vertex i back to itself.
How often does this happen? (sketch proof)
Consider inserting n keys into the table. . .
so use previous result with i = j.. . .
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
i

140. Rehashing
The previous analysis on the expected running time holds when there are no cycles.
However, we would expect there to be cycles every now and then, causing a rehash.
A cycle is a path from a vertex i back to itself.
How often does this happen? (sketch proof)
Consider inserting n keys into the table. . .
so use previous result with i = j.. . .
For any positions i and j, and any constant c > 1, if m 2cn then the probability that there exists a
shortest path in the cuckoo graph from i to j with length 1, is at most 1
c ·m
.
LEMMA
The probability that a position i is involved in a cycle is at most
∞
=1
1
c · m
=
1
m(c − 1)
.
(another union bound over all possible path lengths.)
i

141. Rehashing
The probability that a position i is involved in a cycle is at most
∞
=1
1
c · m
=
1
m(c − 1)
.
(another union bound over all possible path lengths.)

142. Rehashing
The probability that a position i is involved in a cycle is at most
∞
=1
1
c · m
=
1
m(c − 1)
.
The probability that there is at least one cycle is at most
m ·
1
m(c − 1)
=
1
c − 1
.
(another union bound over all possible path lengths.)

143. Rehashing
The probability that a position i is involved in a cycle is at most
∞
=1
1
c · m
=
1
m(c − 1)
.
The probability that there is at least one cycle is at most
m ·
1
m(c − 1)
=
1
c − 1
.
(another union bound over all possible path lengths.)
(union bound over all m positions in the table.)

144. Rehashing
The probability that a position i is involved in a cycle is at most
∞
=1
1
c · m
=
1
m(c − 1)
.
The probability that there is at least one cycle is at most
m ·
1
m(c − 1)
=
1
c − 1
.
If we set c = 3, the probability is at most 1
2 that a cycle occurs
(another union bound over all possible path lengths.)
(union bound over all m positions in the table.)
(that there is a rehash) during the n insertions.

145. Rehashing
The probability that a position i is involved in a cycle is at most
∞
=1
1
c · m
=
1
m(c − 1)
.
The probability that there is at least one cycle is at most
m ·
1
m(c − 1)
=
1
c − 1
.
If we set c = 3, the probability is at most 1
2 that a cycle occurs
The probability that there are two rehashes is 1
4 , and so on.
(another union bound over all possible path lengths.)
(union bound over all m positions in the table.)
(that there is a rehash) during the n insertions.

146. Rehashing
The probability that a position i is involved in a cycle is at most
∞
=1
1
c · m
=
1
m(c − 1)
.
The probability that there is at least one cycle is at most
m ·
1
m(c − 1)
=
1
c − 1
.
If we set c = 3, the probability is at most 1
2 that a cycle occurs
The probability that there are two rehashes is 1
4 , and so on.
So the expected number of rehashes during n insertions is at most
∞
i=1
1
2
i
= 1.
(another union bound over all possible path lengths.)
(union bound over all m positions in the table.)
(that there is a rehash) during the n insertions.

147. Rehashing
If the expected time for one rehash is O(n) then
the expected time for all rehashes is also O(n)
(this is because we only expect there to be one rehash).

148. Rehashing
If the expected time for one rehash is O(n) then
Therefore the amortised expected time for the rehashes over the n insertions is
the expected time for all rehashes is also O(n)
(this is because we only expect there to be one rehash).
O(1) per insertion (i.e. divide the total cost with n).

149. Rehashing
If the expected time for one rehash is O(n) then
Therefore the amortised expected time for the rehashes over the n insertions is
Why is the expected time per rehash O(n)?
the expected time for all rehashes is also O(n)
(this is because we only expect there to be one rehash).
O(1) per insertion (i.e. divide the total cost with n).

150. Rehashing
If the expected time for one rehash is O(n) then
Therefore the amortised expected time for the rehashes over the n insertions is
Why is the expected time per rehash O(n)?
First pick a new random h1 and h2 and construct the cuckoo graph
the expected time for all rehashes is also O(n)
(this is because we only expect there to be one rehash).
O(1) per insertion (i.e. divide the total cost with n).
using the at most n keys.

151. Rehashing
If the expected time for one rehash is O(n) then
Therefore the amortised expected time for the rehashes over the n insertions is
Why is the expected time per rehash O(n)?
First pick a new random h1 and h2 and construct the cuckoo graph
the expected time for all rehashes is also O(n)
(this is because we only expect there to be one rehash).
O(1) per insertion (i.e. divide the total cost with n).
using the at most n keys.
Check for a cycle in the graph in O(n) time (and start again if you find one)

152. Rehashing
If the expected time for one rehash is O(n) then
Therefore the amortised expected time for the rehashes over the n insertions is
Why is the expected time per rehash O(n)?
First pick a new random h1 and h2 and construct the cuckoo graph
the expected time for all rehashes is also O(n)
(this is because we only expect there to be one rehash).
O(1) per insertion (i.e. divide the total cost with n).
using the at most n keys.
Check for a cycle in the graph in O(n) time (and start again if you find one)
(you can do this using breadth-first search)

153. Rehashing
If the expected time for one rehash is O(n) then
Therefore the amortised expected time for the rehashes over the n insertions is
Why is the expected time per rehash O(n)?
If there is no cycle, insert all the elements,
First pick a new random h1 and h2 and construct the cuckoo graph
the expected time for all rehashes is also O(n)
(this is because we only expect there to be one rehash).
O(1) per insertion (i.e. divide the total cost with n).
using the at most n keys.
Check for a cycle in the graph in O(n) time (and start again if you find one)
(you can do this using breadth-first search)
this takes O(n) time in expectation (as we have seen).

154. A word about the assumptions
We have assumed true randomness. As we have discussed, this is not realistic.

155. A word about the assumptions
We have assumed true randomness. As we have discussed, this is not realistic.
We have seen that weakly universal hash families are realistic
where any two keys x, y are independent

156. A word about the assumptions
We have assumed true randomness. As we have discussed, this is not realistic.
We have seen that weakly universal hash families are realistic
where any two keys x, y are independent
A set H of hash functions is weakly universal if for any two distinct keys x, y ∈ U,
Pr h(x) = h(y) 1
m (where h is picked uniformly at random from H)

157. A word about the assumptions
We have assumed true randomness. As we have discussed, this is not realistic.
We have seen that weakly universal hash families are realistic
We can define a stronger hash families with k-wise independence.
here the hash values of any choice of k keys are independent.
where any two keys x, y are independent
A set H of hash functions is weakly universal if for any two distinct keys x, y ∈ U,
Pr h(x) = h(y) 1
m (where h is picked uniformly at random from H)

158. A word about the assumptions
We have assumed true randomness. As we have discussed, this is not realistic.
We have seen that weakly universal hash families are realistic
We can define a stronger hash families with k-wise independence.
here the hash values of any choice of k keys are independent.
where any two keys x, y are independent
A set H of hash functions is weakly universal if for any two distinct keys x, y ∈ U,
Pr h(x) = h(y) 1
m (where h is picked uniformly at random from H)
A set H of hash functions is k-wise independent if
for any k distinct keys x1, x2 . . . xk ∈ U and k values v1, v2, . . . vk ∈ {0, 1, 2 . . . m − 1},
Pr


i
h(xi) = vi

 =
1
mk
(where h is picked uniformly at random from H)

159. A word about the assumptions
We have assumed true randomness. As we have discussed, this is not realistic.
We have seen that weakly universal hash families are realistic
We can define a stronger hash families with k-wise independence.
here the hash values of any choice of k keys are independent.
where any two keys x, y are independent

160. A word about the assumptions
We have assumed true randomness. As we have discussed, this is not realistic.
We have seen that weakly universal hash families are realistic
We can define a stronger hash families with k-wise independence.
here the hash values of any choice of k keys are independent.
where any two keys x, y are independent

161. A word about the assumptions
We have assumed true randomness. As we have discussed, this is not realistic.
We have seen that weakly universal hash families are realistic
We can define a stronger hash families with k-wise independence.
here the hash values of any choice of k keys are independent.
where any two keys x, y are independent
It is feasible to construct a (log n)-wise independent family of hash functions
such that h(x) can be computed in O(1) time

162. A word about the assumptions
We have assumed true randomness. As we have discussed, this is not realistic.
We have seen that weakly universal hash families are realistic
We can define a stronger hash families with k-wise independence.
here the hash values of any choice of k keys are independent.
where any two keys x, y are independent
It is feasible to construct a (log n)-wise independent family of hash functions
such that h(x) can be computed in O(1) time
By changing the cuckoo hashing algorithm to perform a rehash after log n moves
it can be shown (via a similar but harder proof) that the results still hold

163. A word about the assumptions
We have assumed true randomness. As we have discussed, this is not realistic.
We have seen that weakly universal hash families are realistic
We can define a stronger hash families with k-wise independence.
here the hash values of any choice of k keys are independent.
where any two keys x, y are independent
THEOREM
In the Cuckoo hashing scheme:
• Every lookup and every delete takes O(1) worst-case time,
• The space is O(n) where n is the number of keys stored
• An insert takes amortised expected O(1) time
It is feasible to construct a (log n)-wise independent family of hash functions
such that h(x) can be computed in O(1) time
By changing the cuckoo hashing algorithm to perform a rehash after log n moves
it can be shown (via a similar but harder proof) that the results still hold