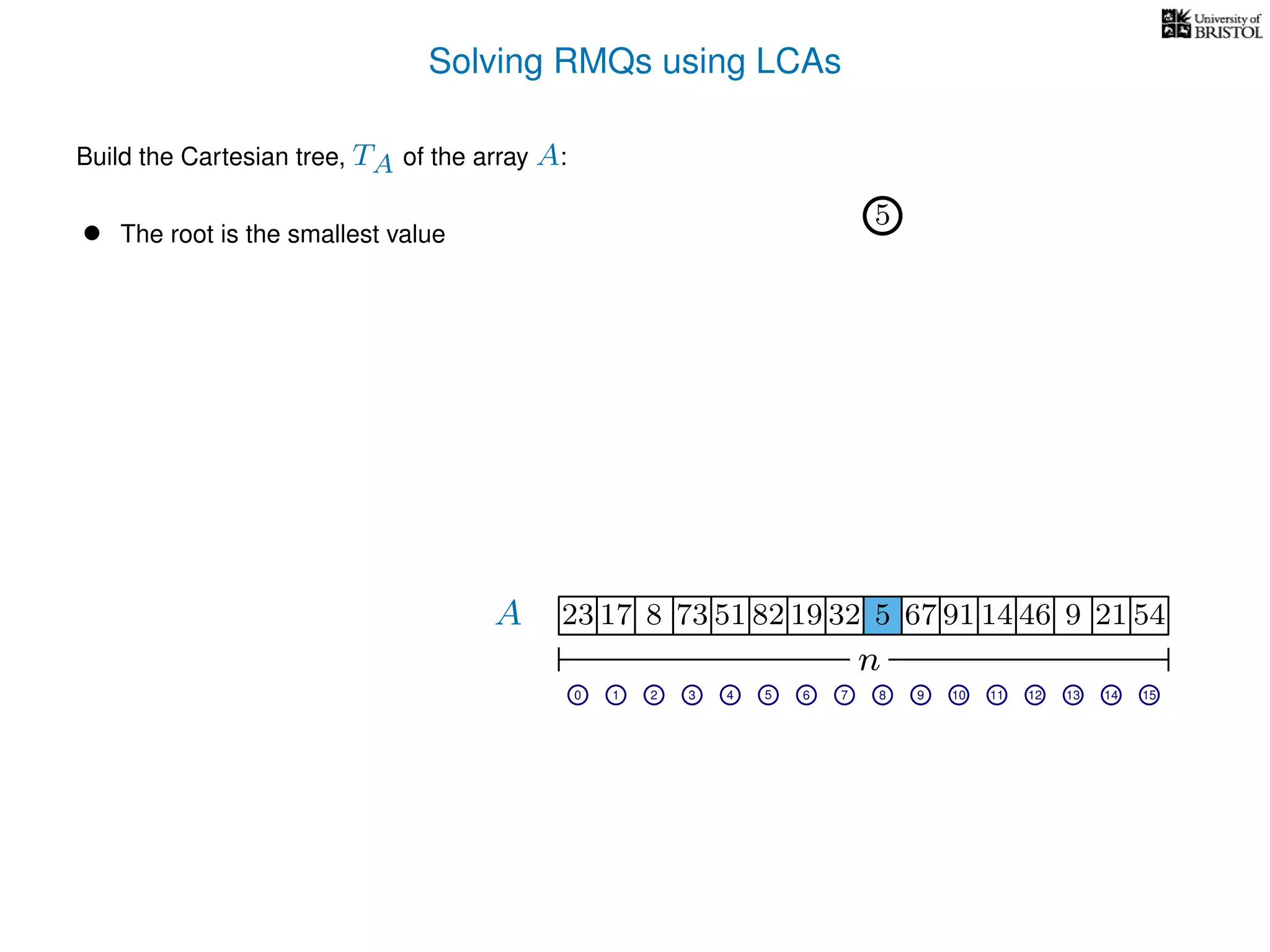
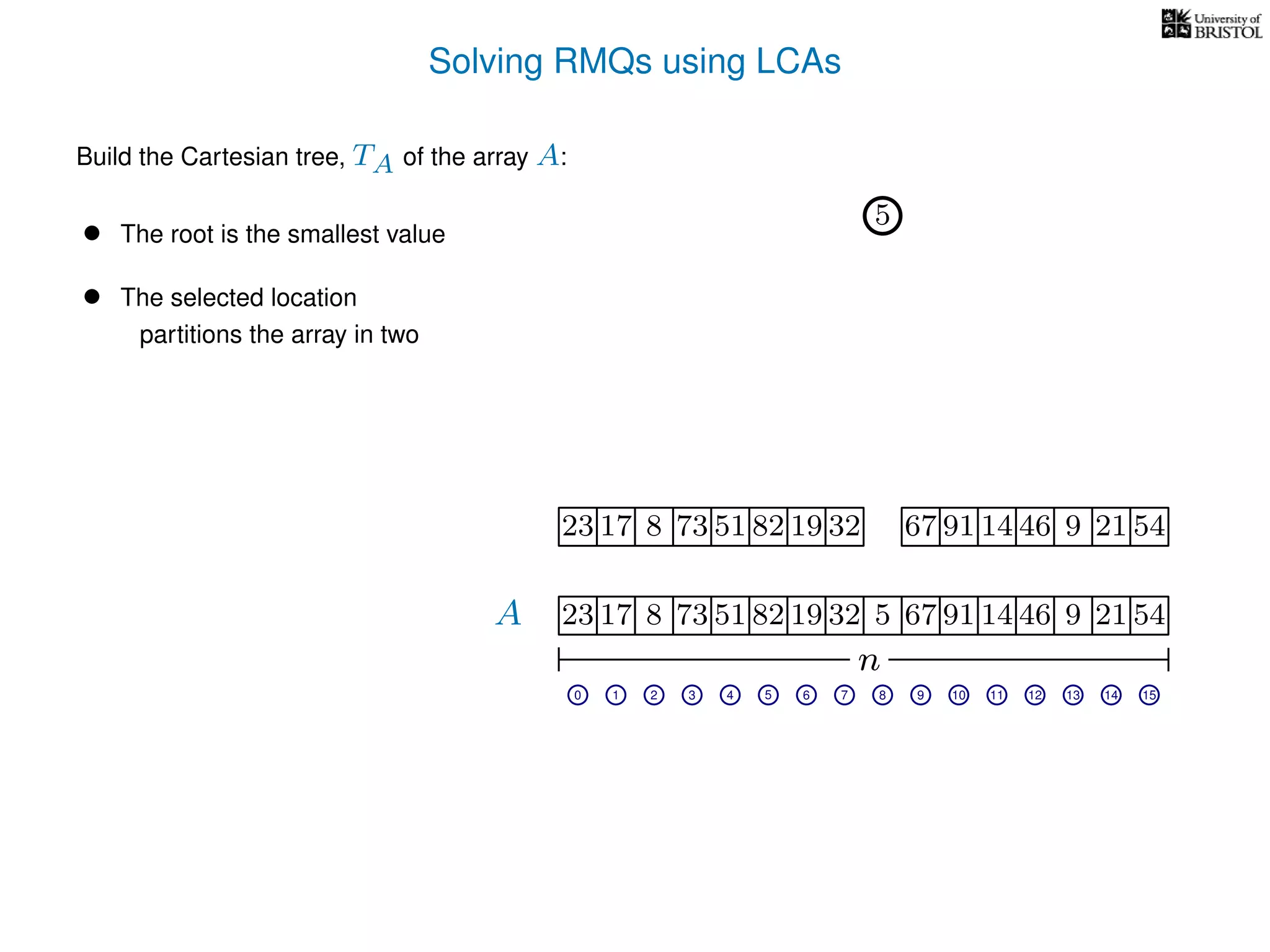
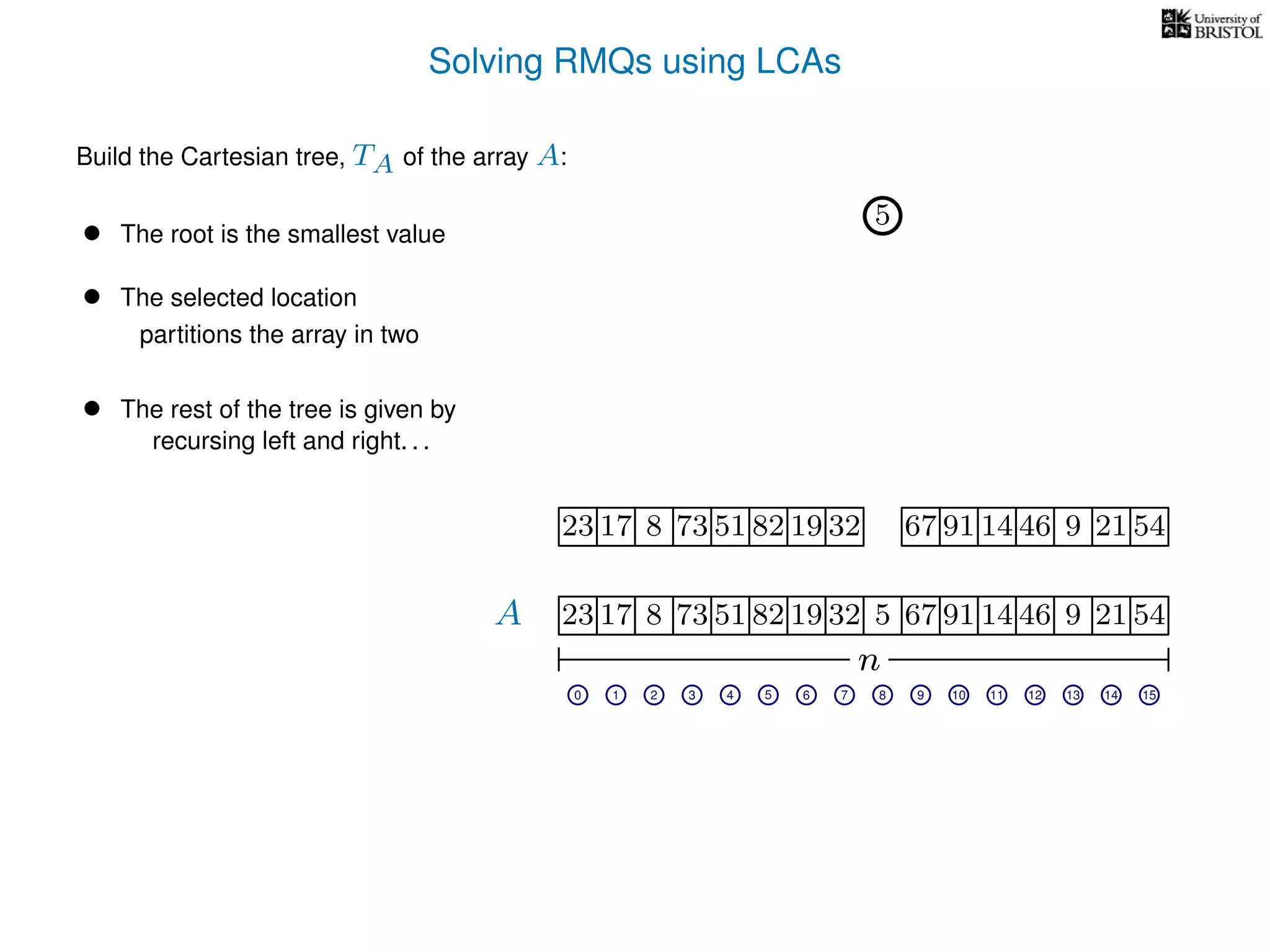
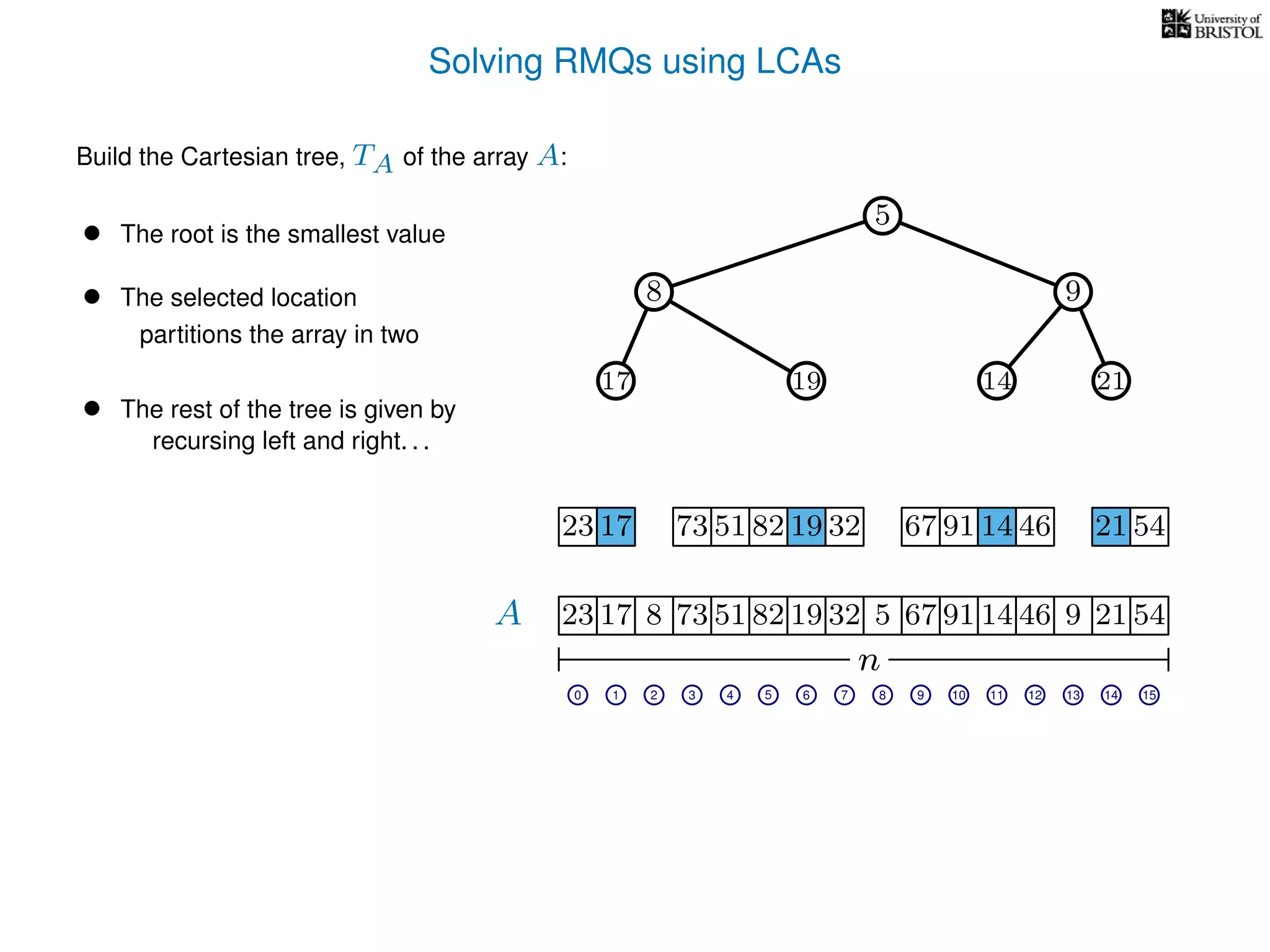
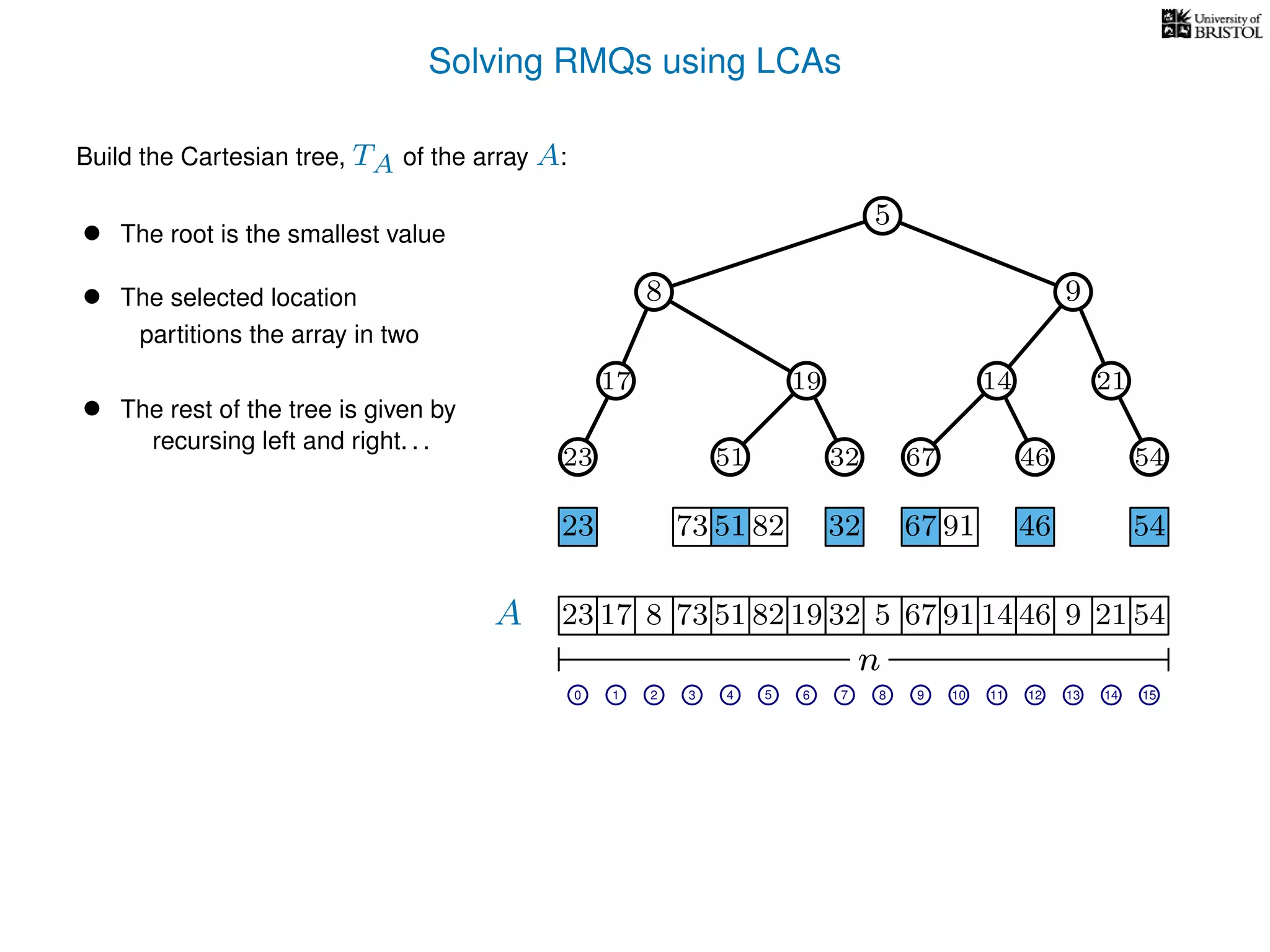
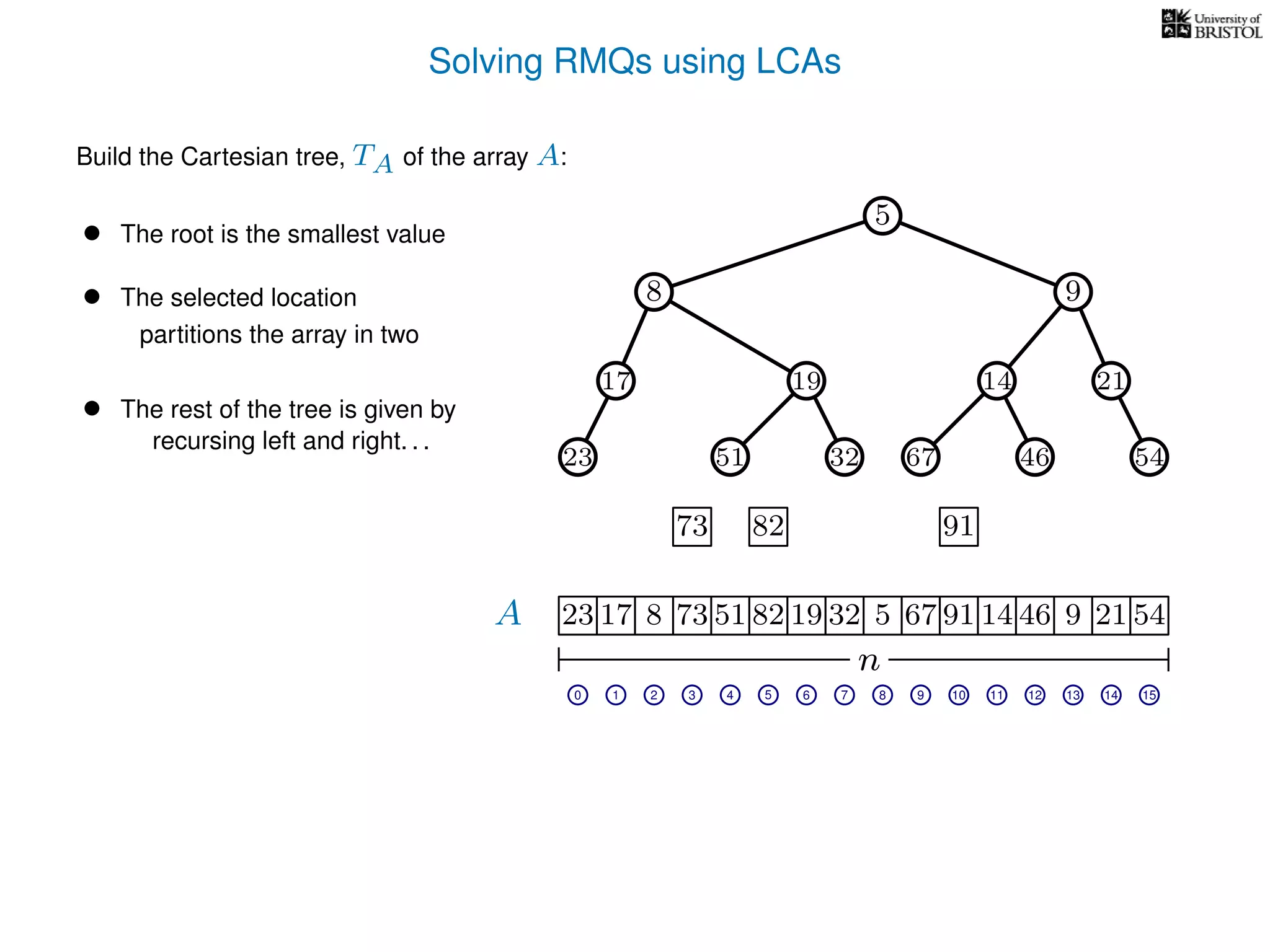
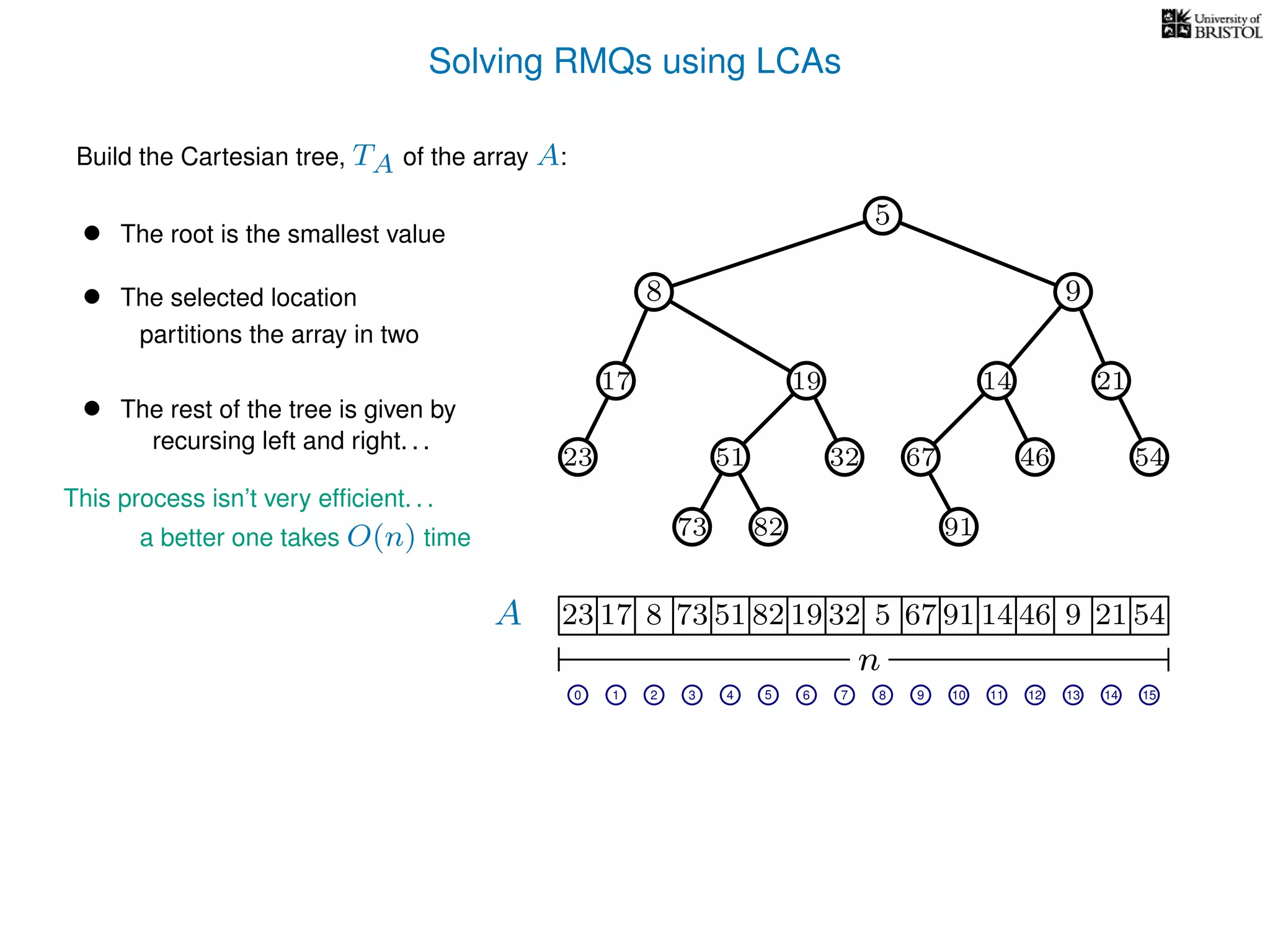
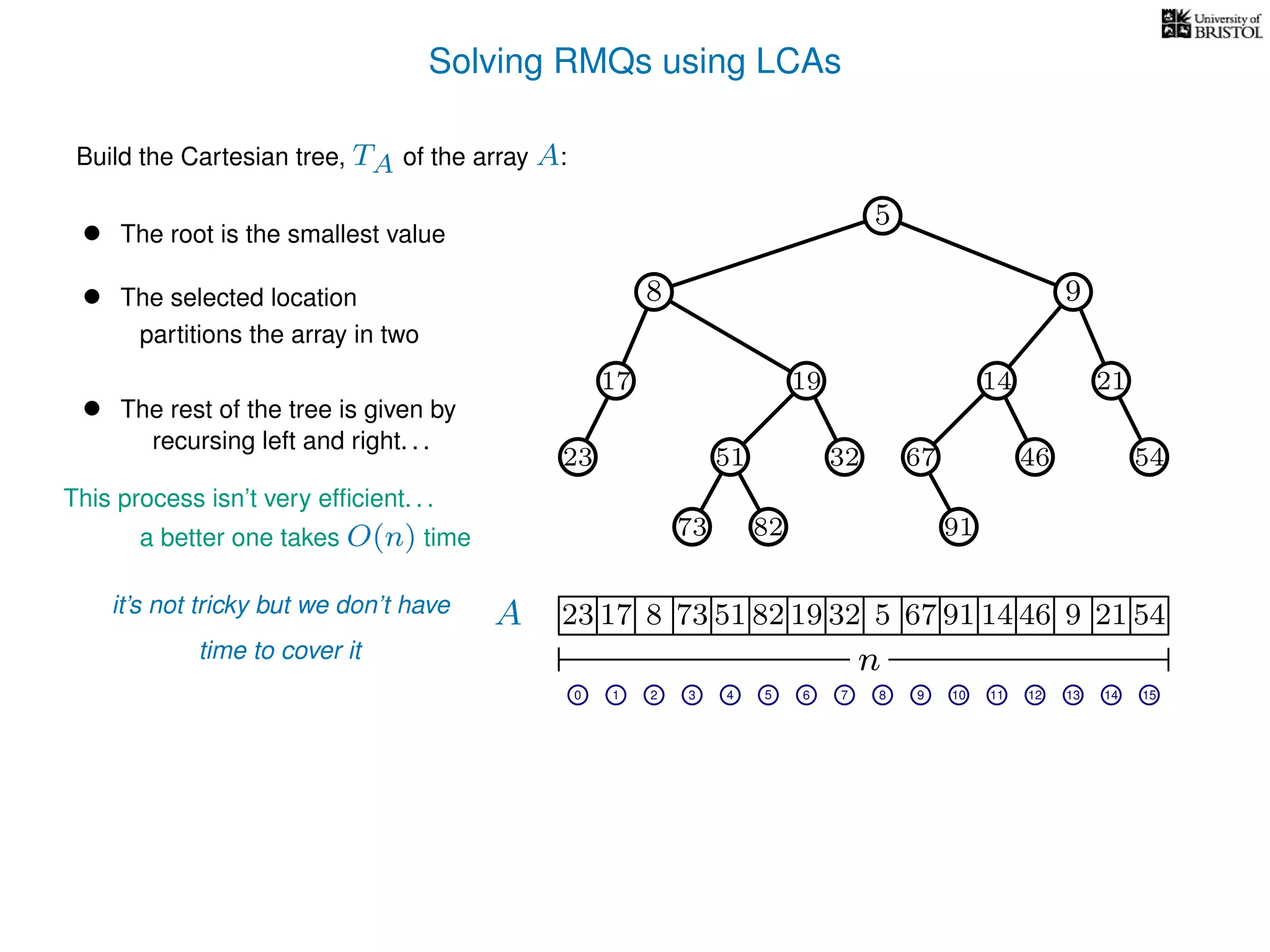
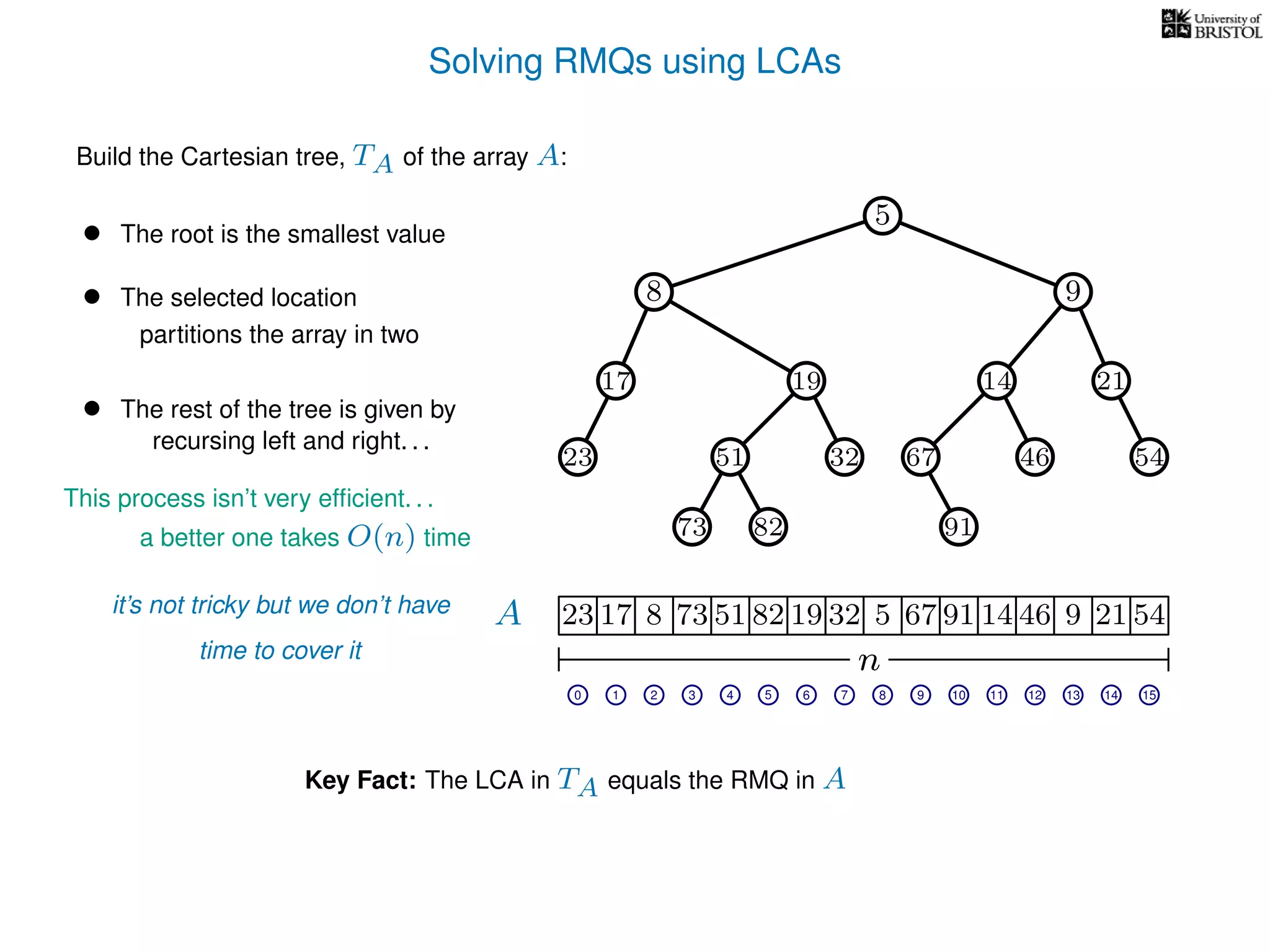
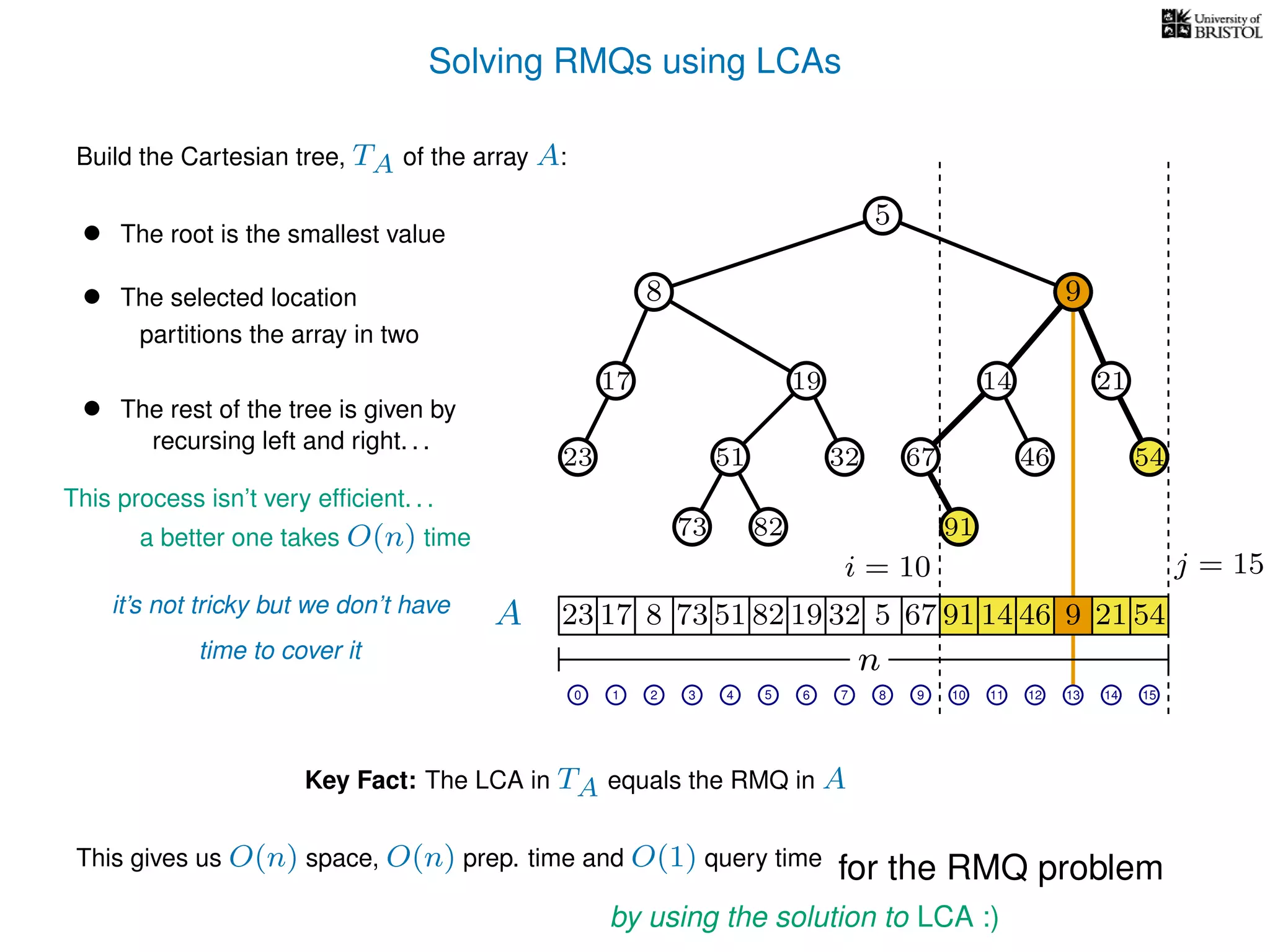
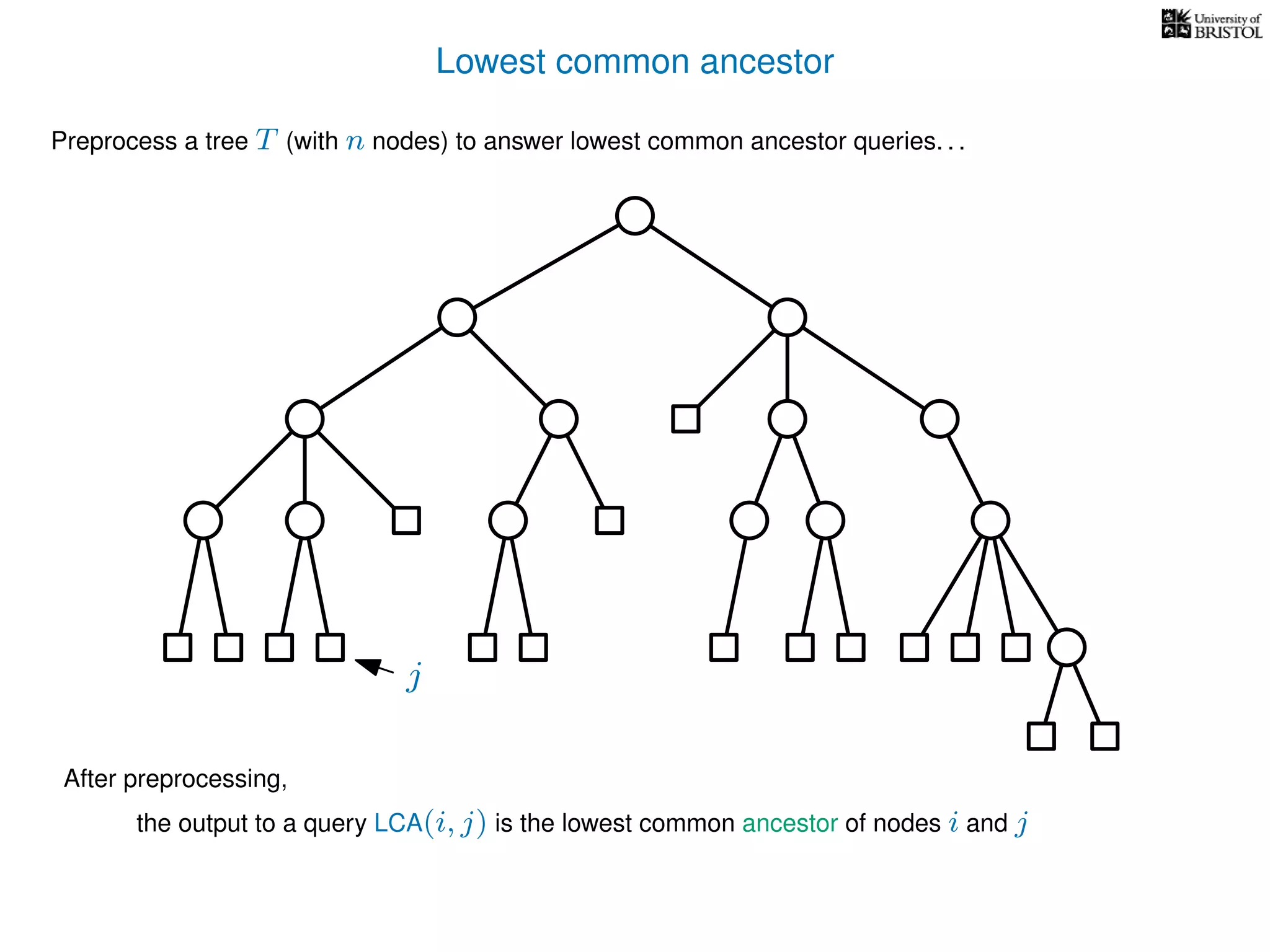
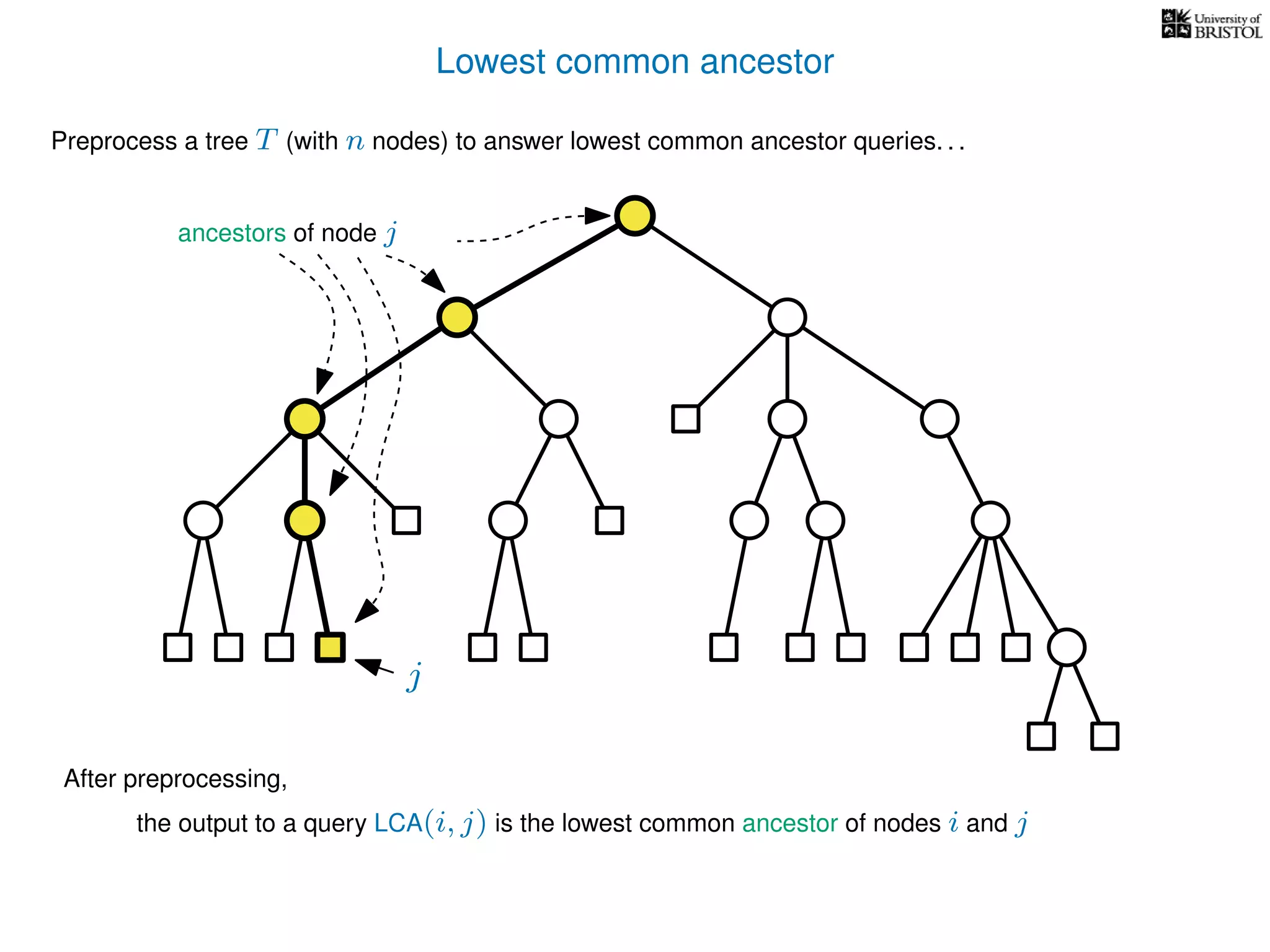
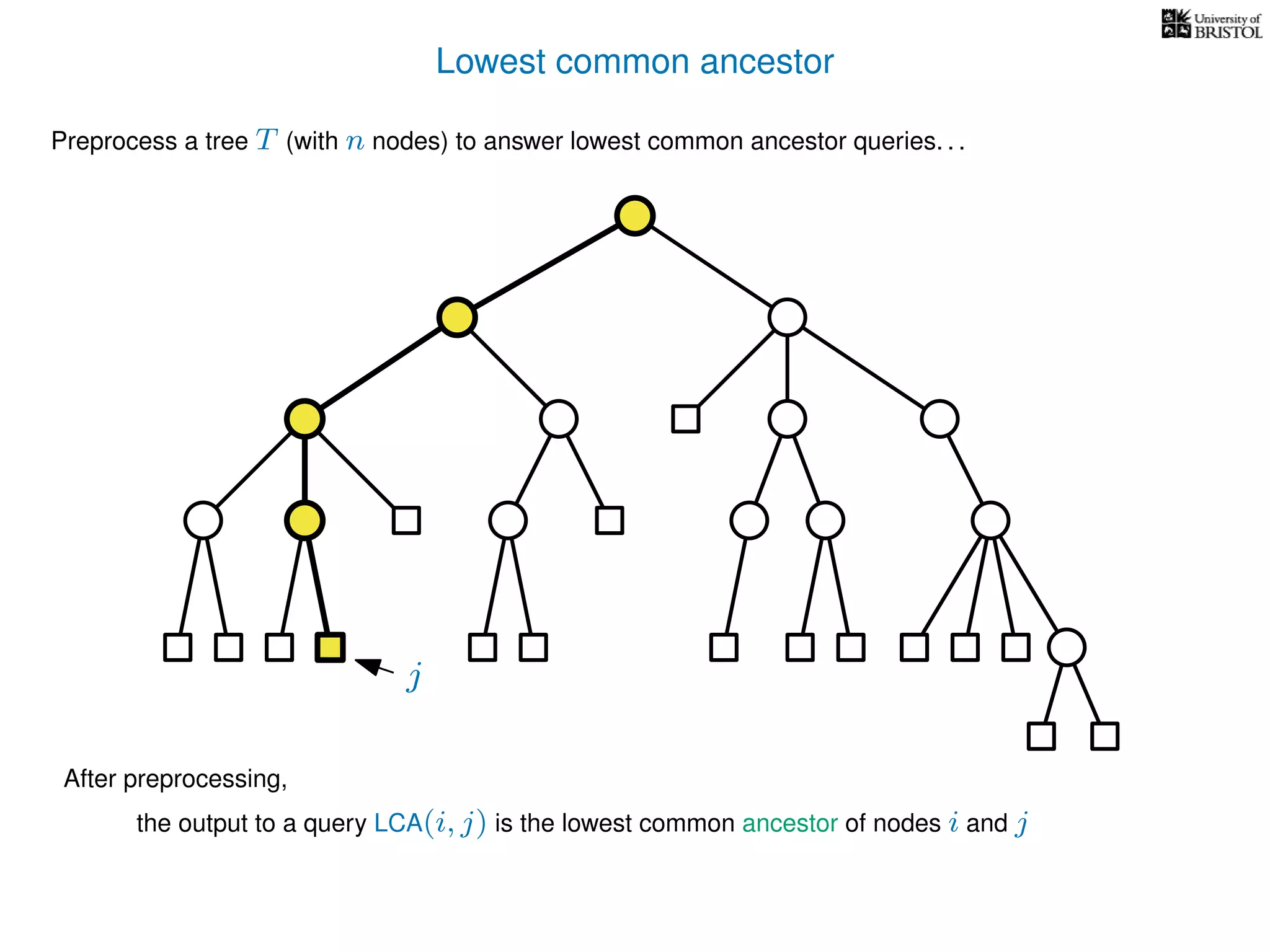
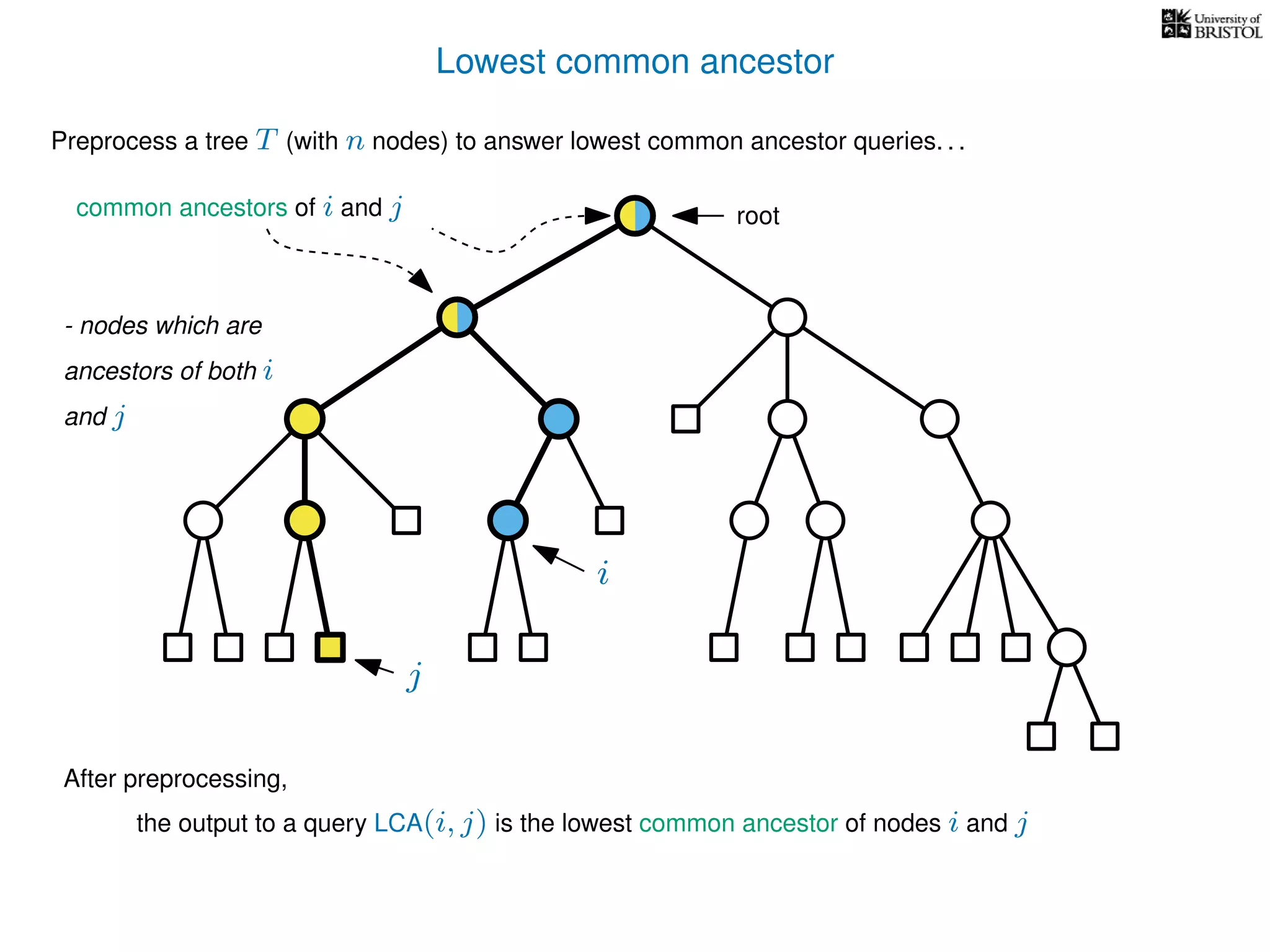
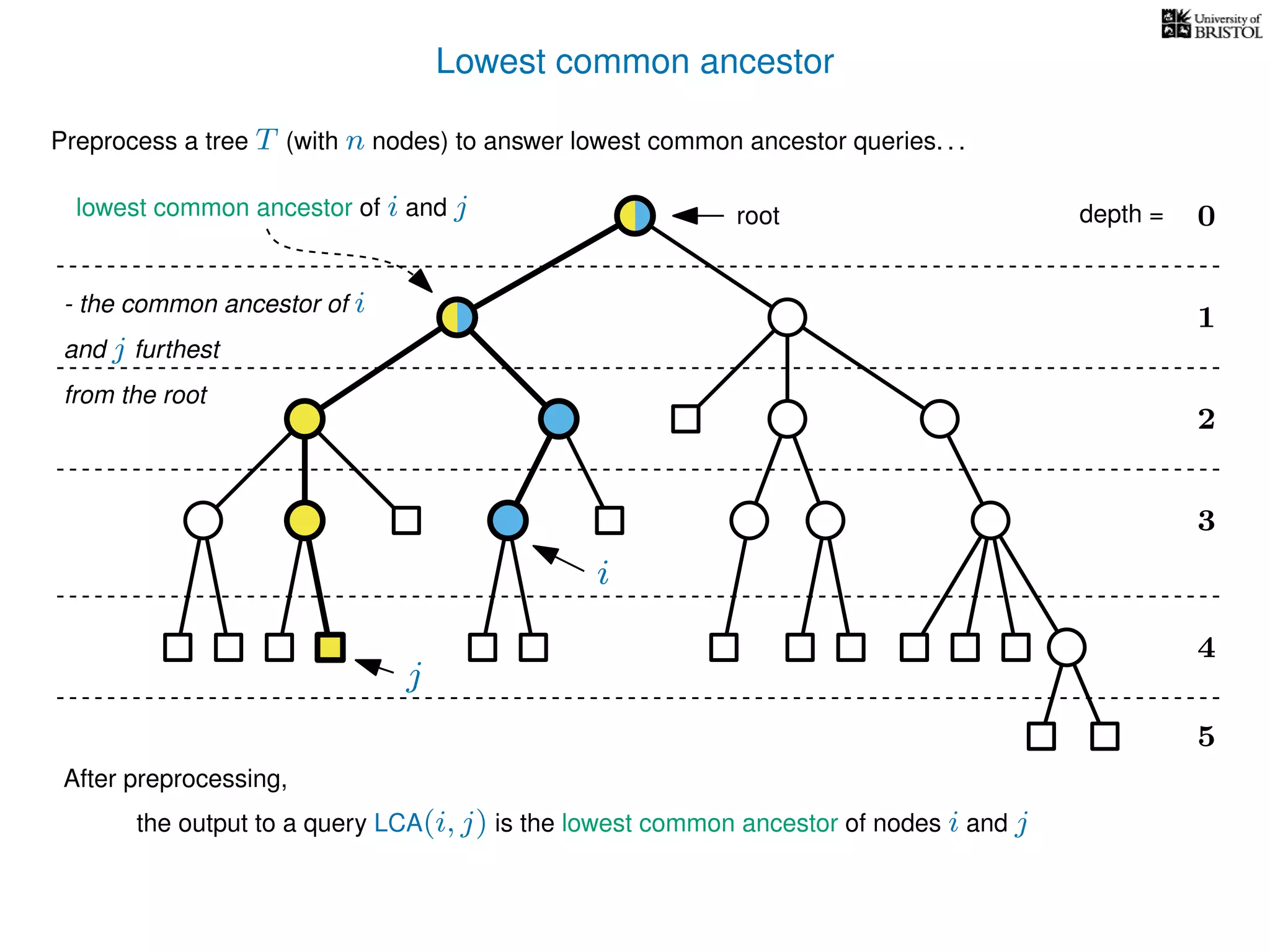
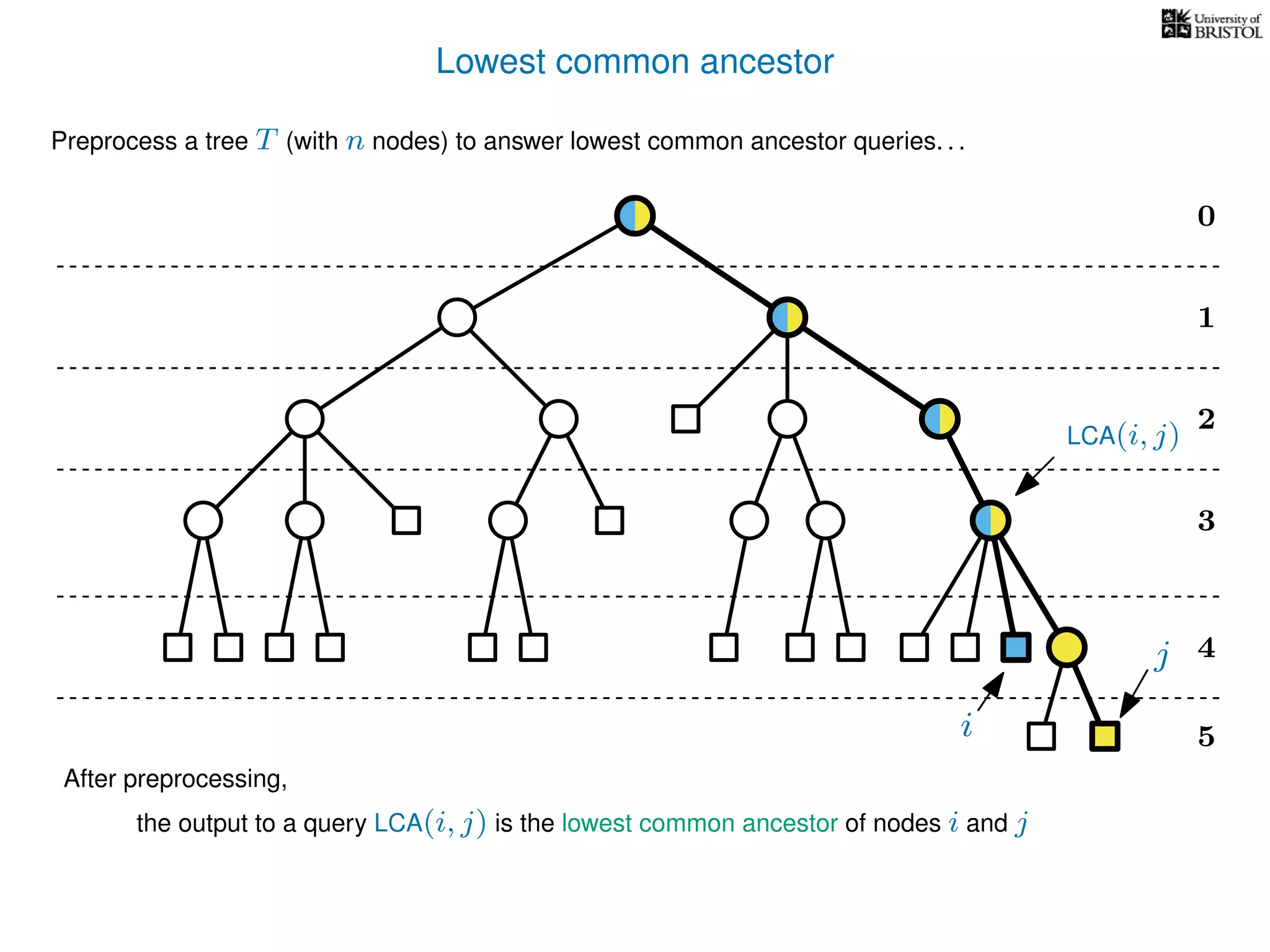
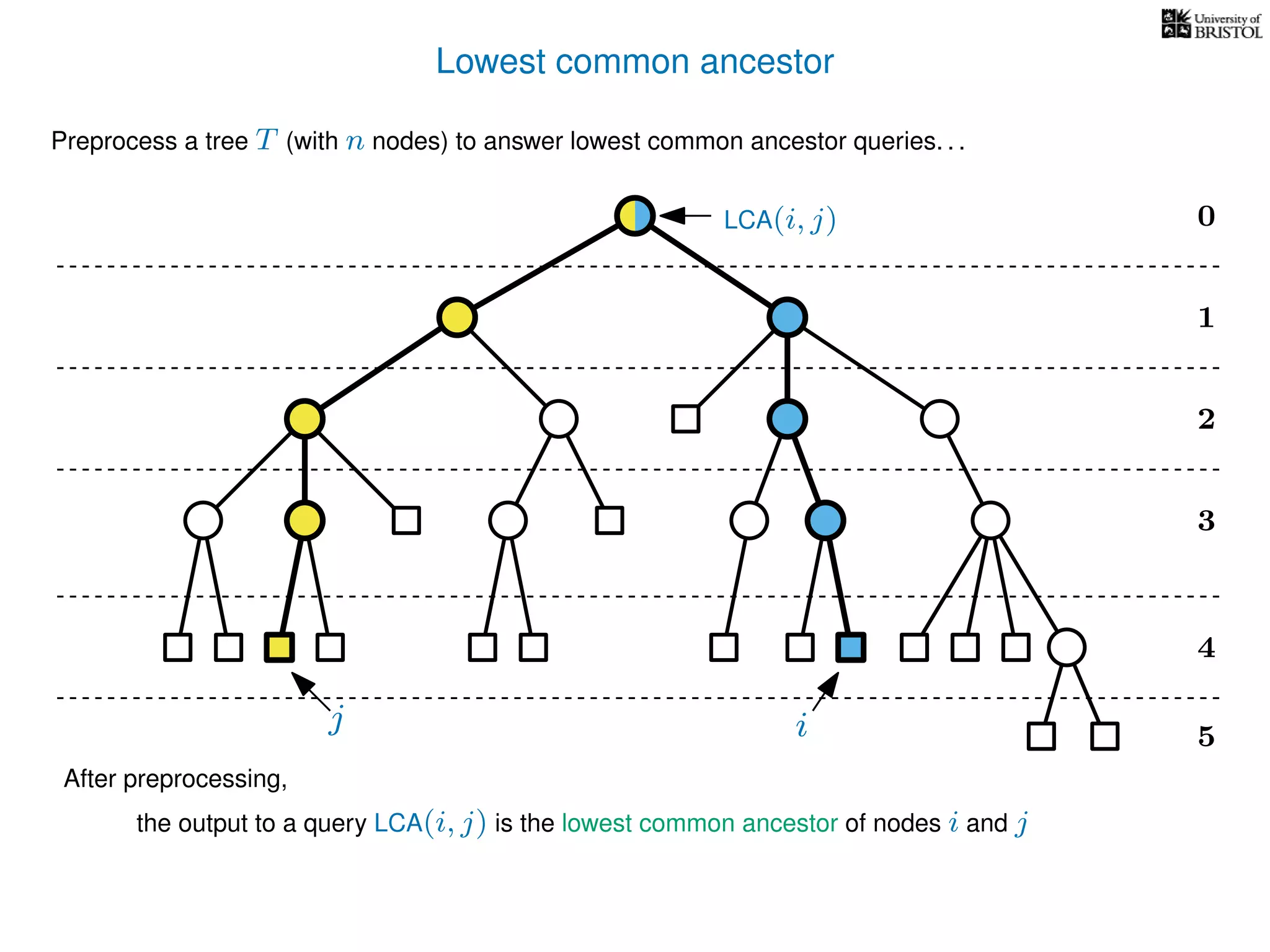
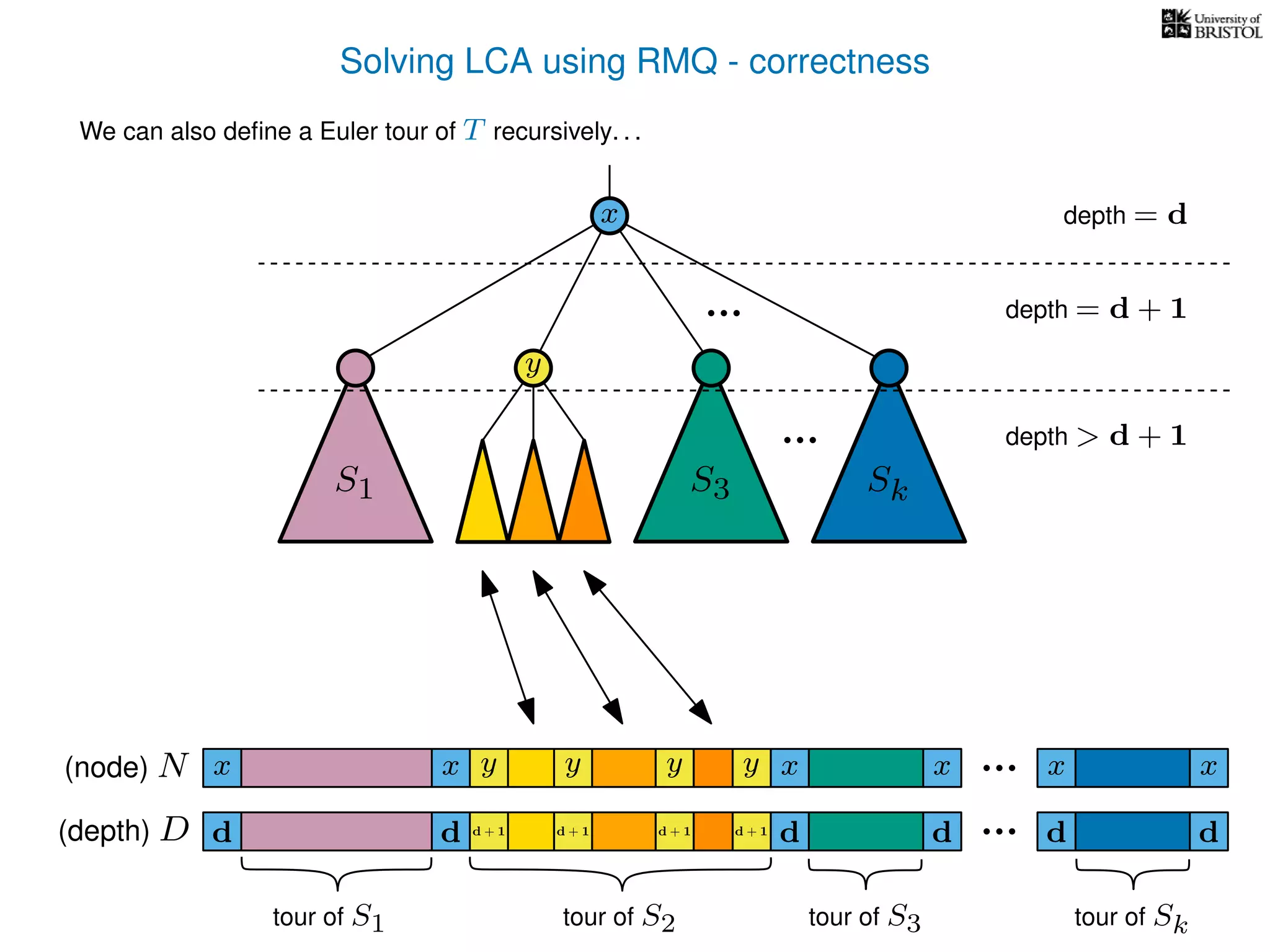
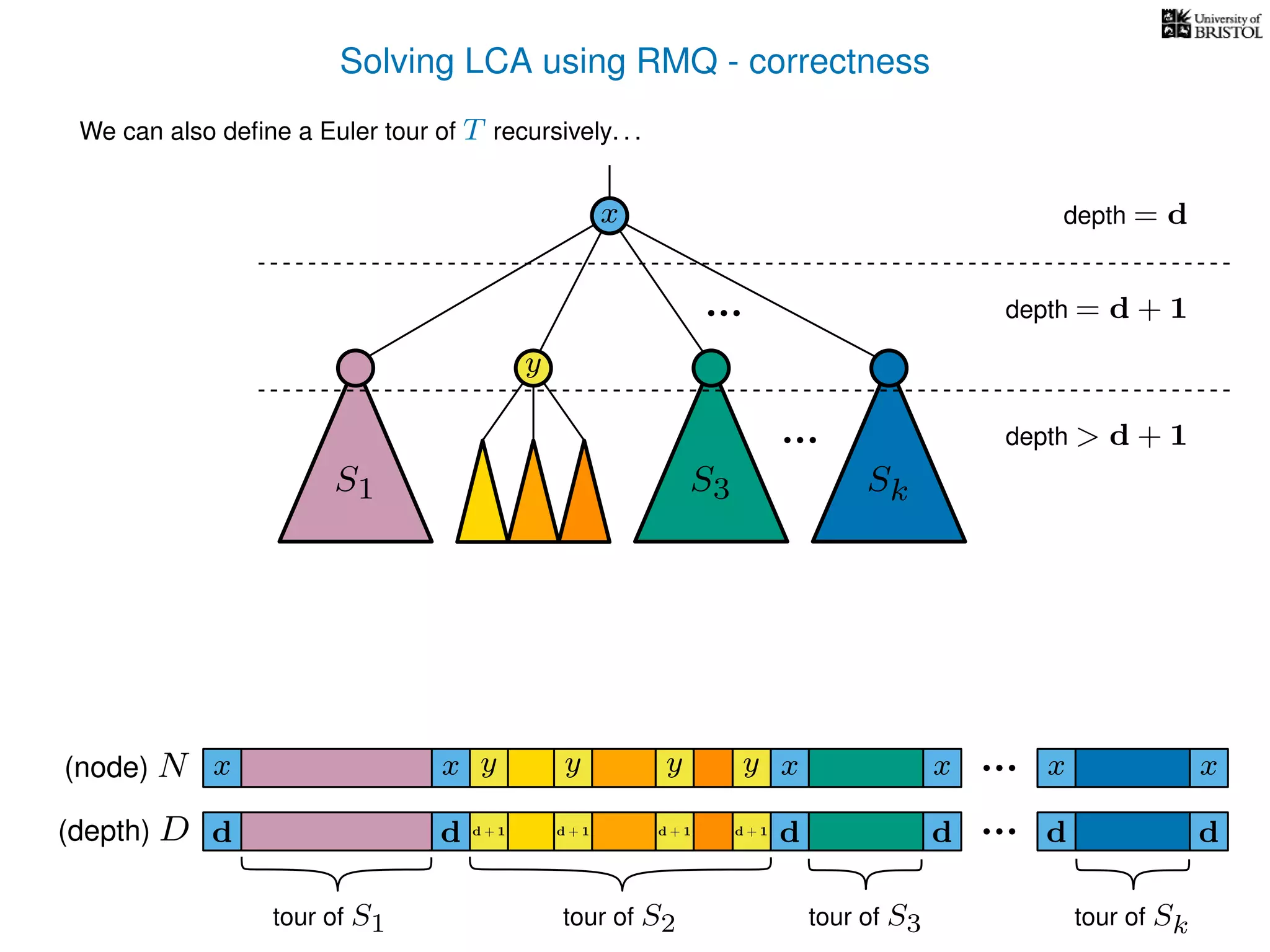
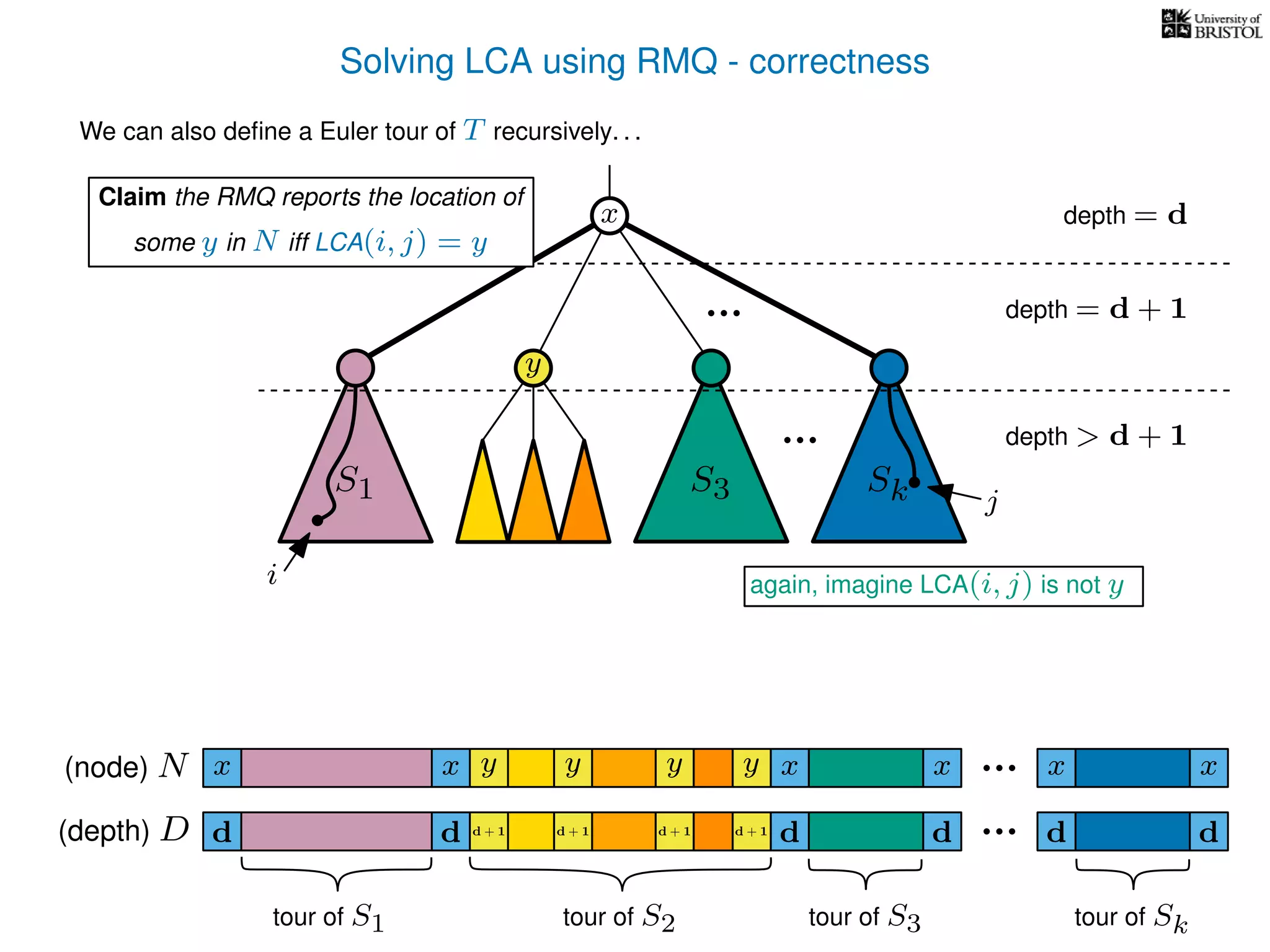
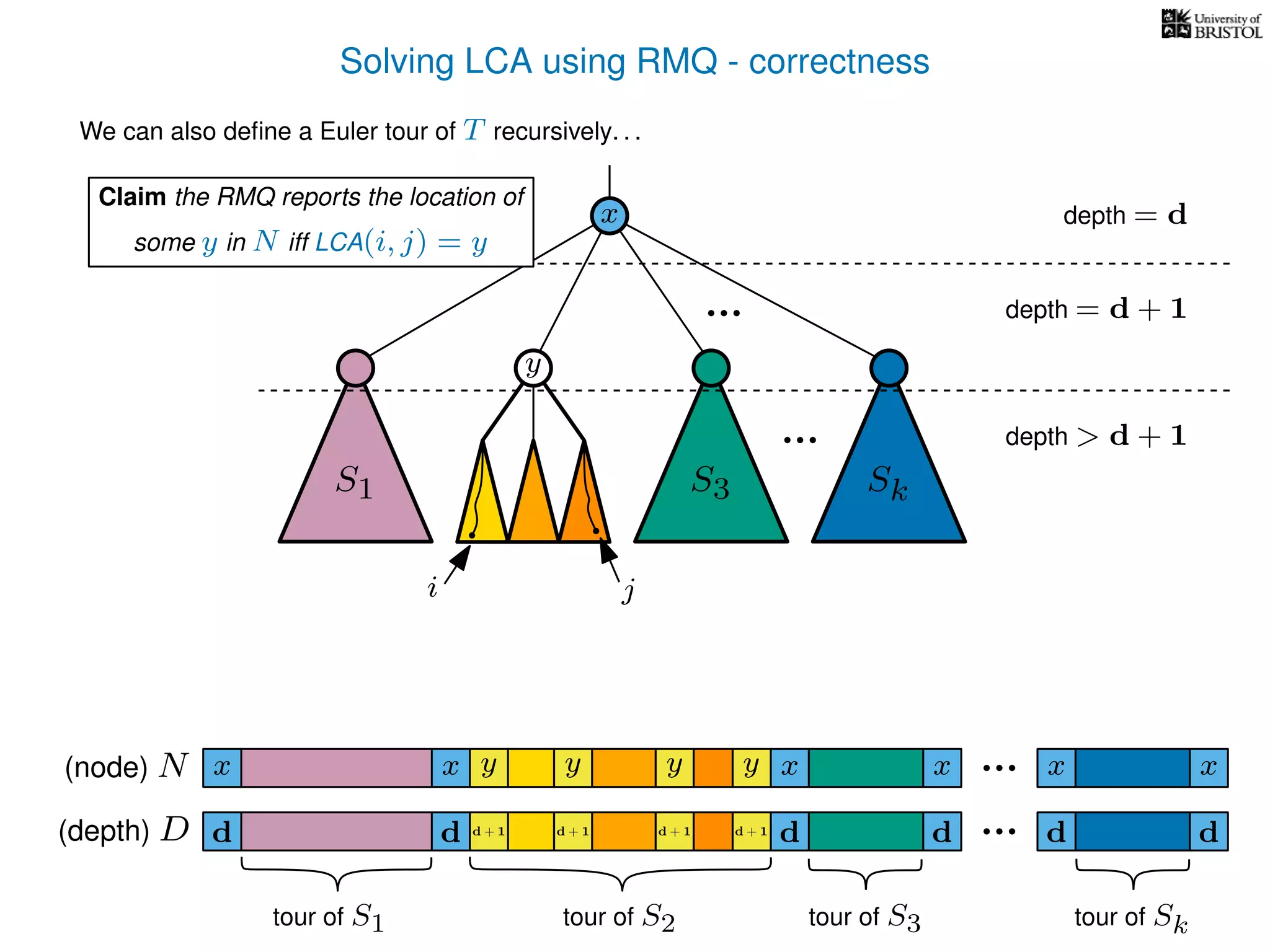
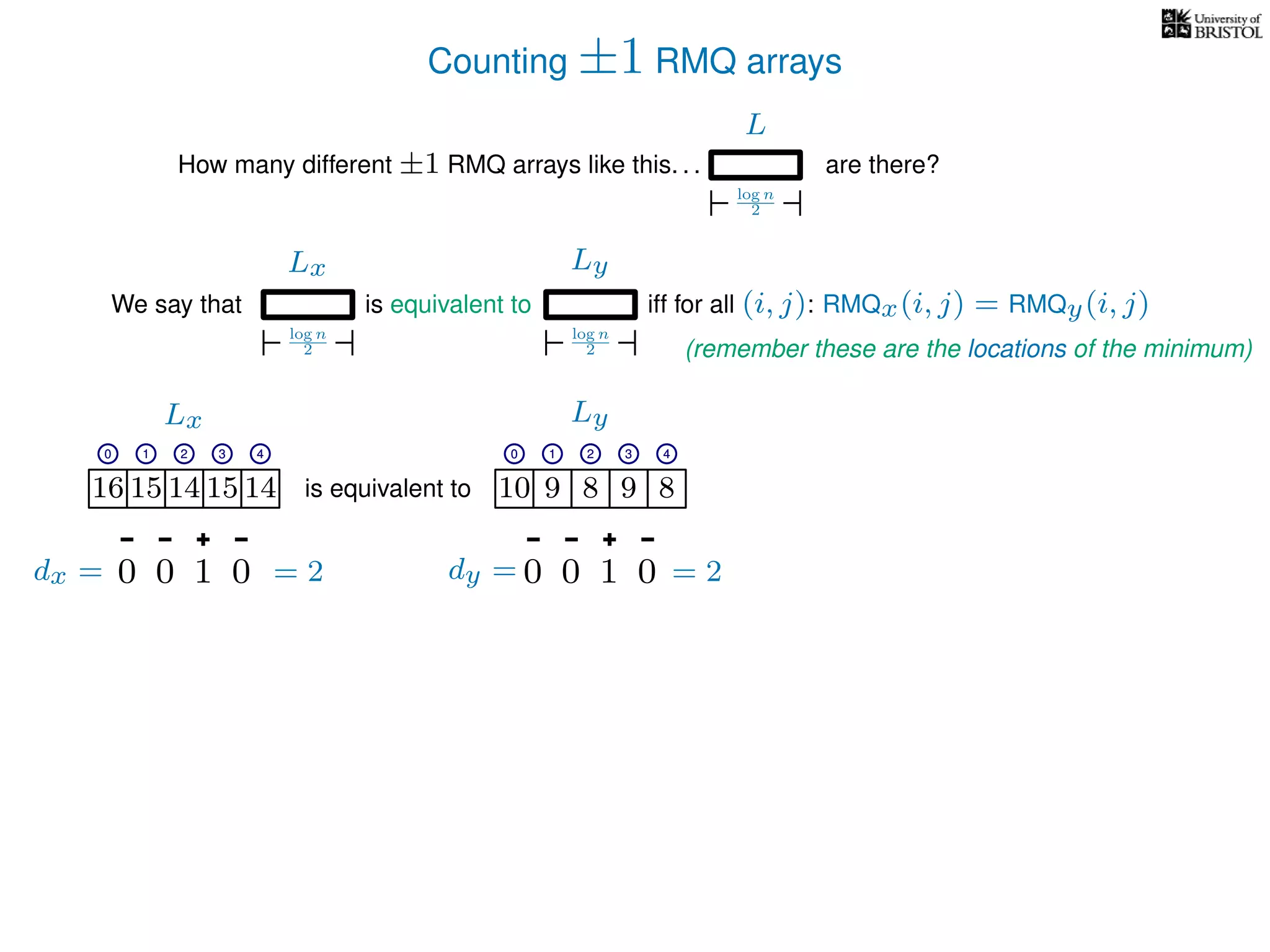
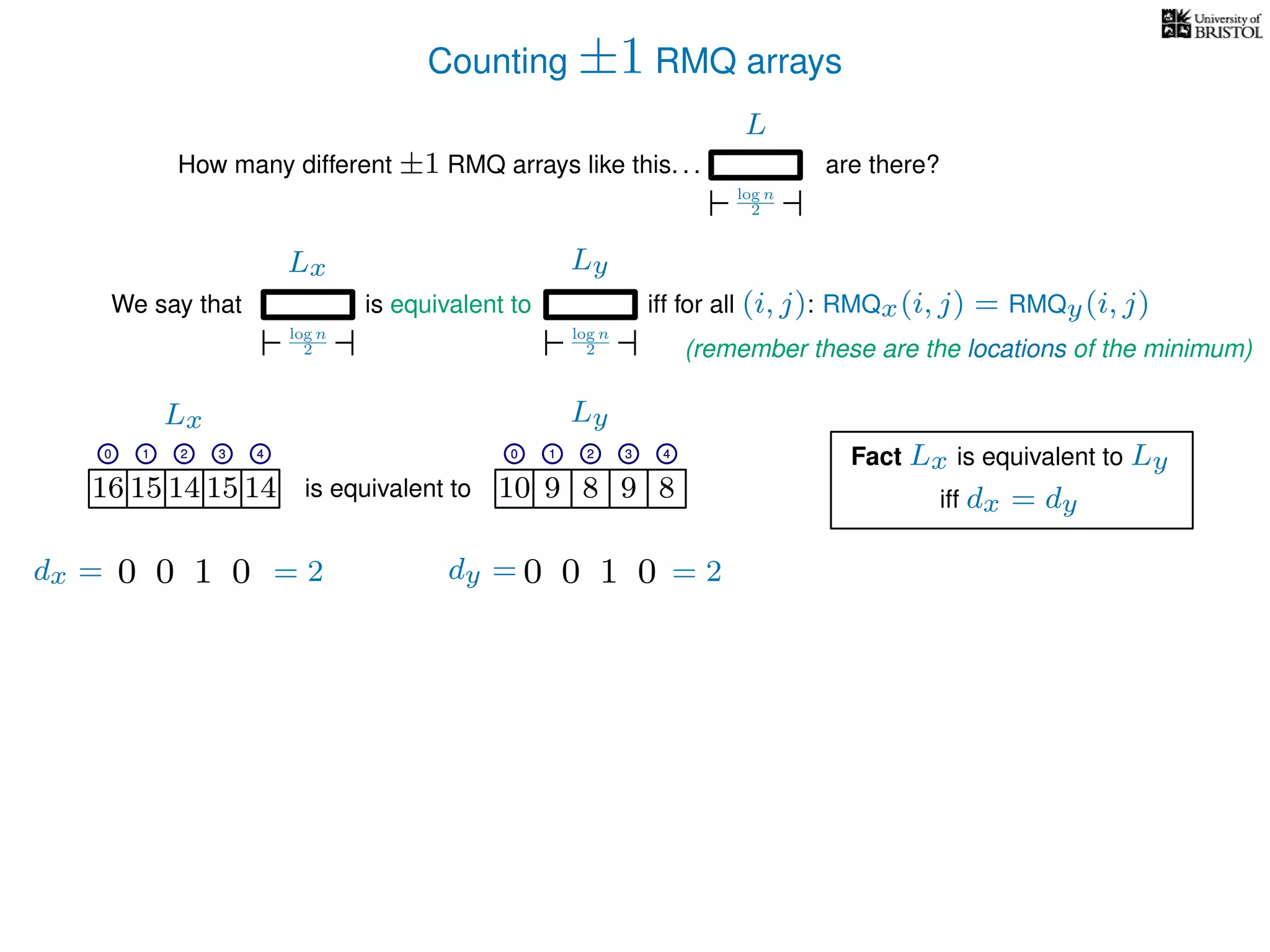
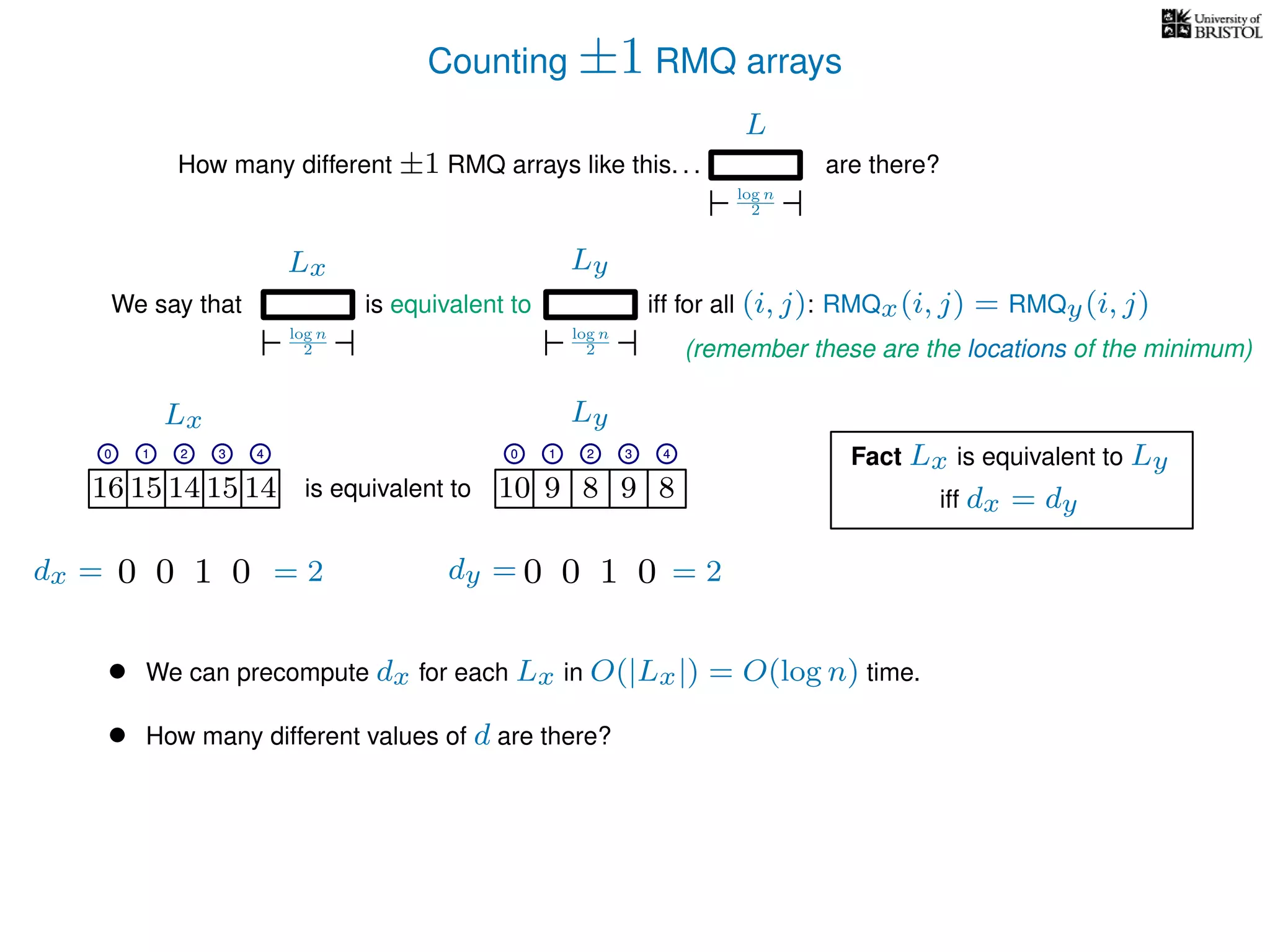
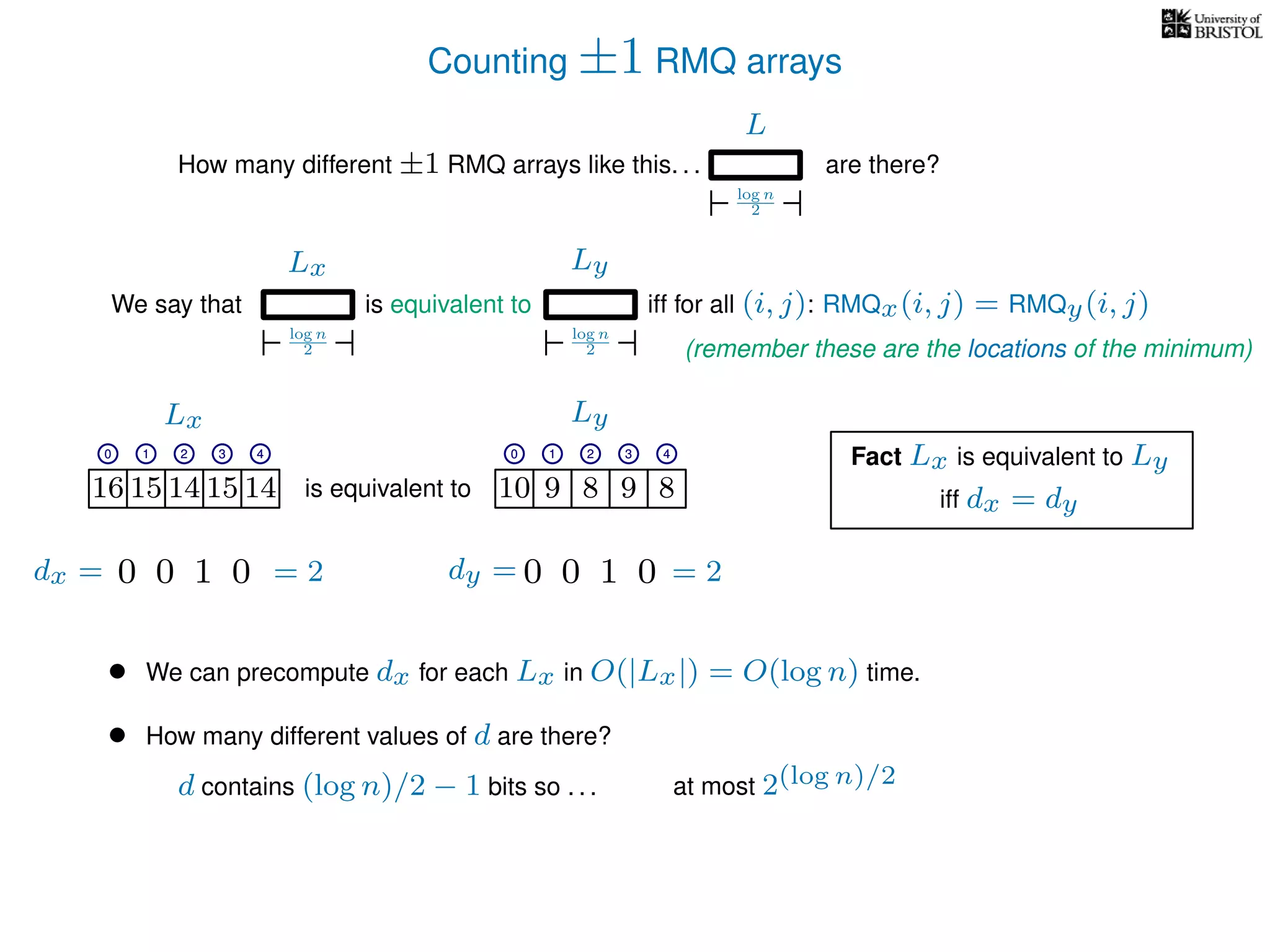
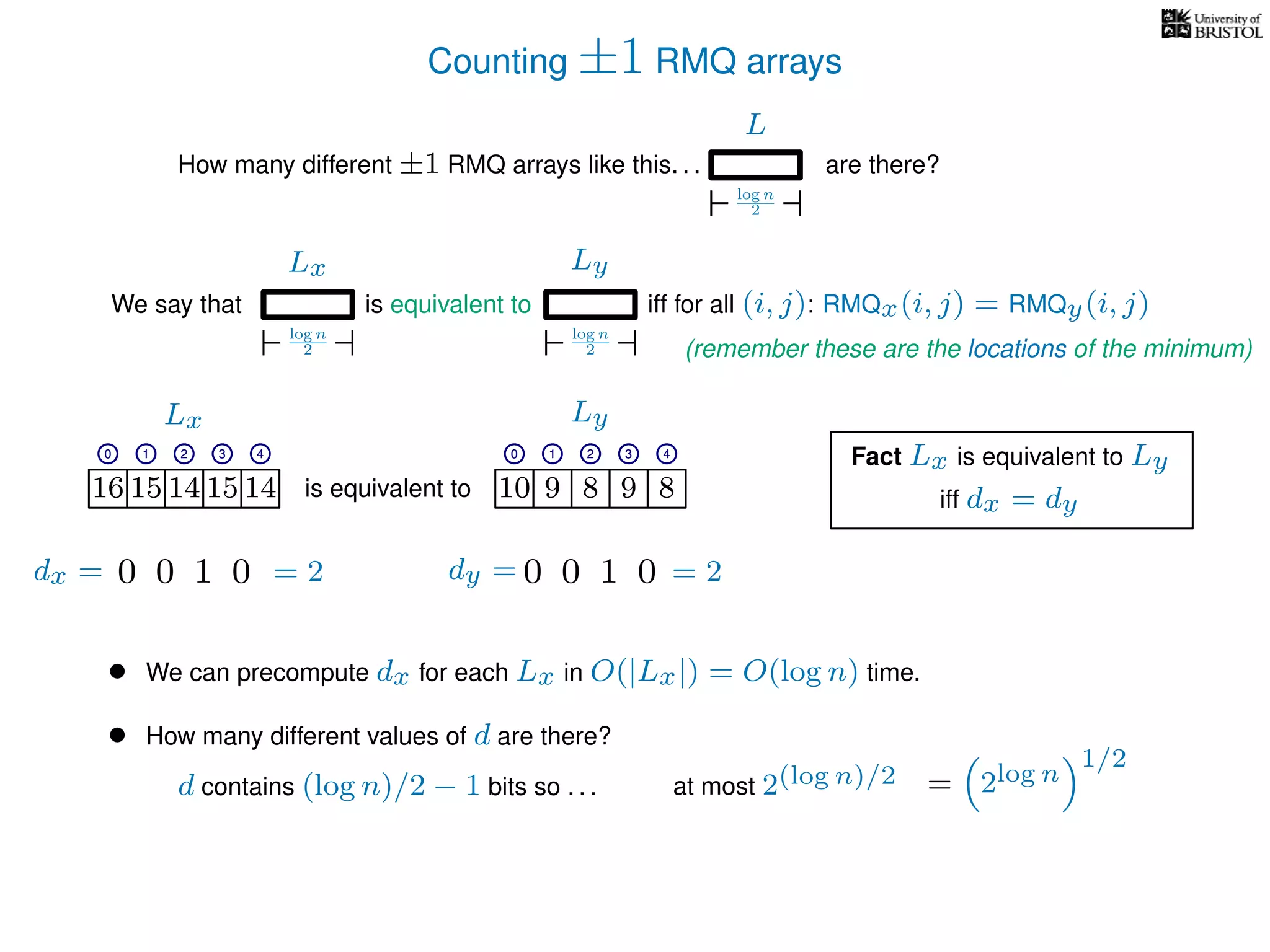
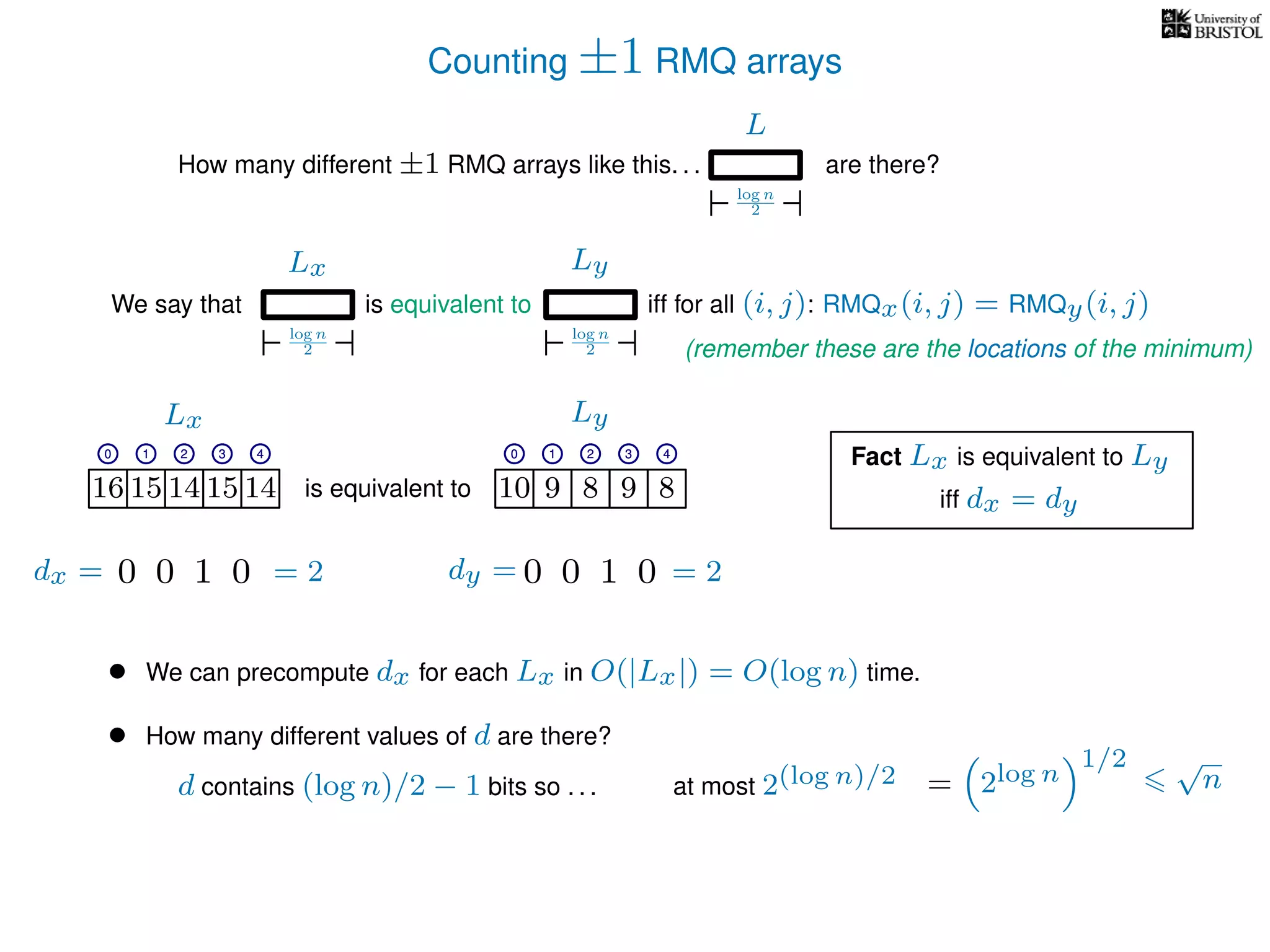
The document discusses algorithms for finding the lowest common ancestor (LCA) in a tree with n nodes, emphasizing the preprocessing required to efficiently answer queries. It outlines the structure needed to handle various LCA queries, and hints at using Euler tours and range minimum queries as methods for optimization. Additionally, it mentions ideal time and space complexities for effective LCA solutions.

1. Advanced Algorithms – COMS31900
Lowest Common Ancestor
(with a bit on on Range Minimum Queries)
Benjamin Sach

2. Advanced Algorithms – COMS31900
Benjamin Sach
Lowest Common Ancestor
(with a bit on on Range Minimum Queries)

3. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .

4. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
After preprocessing,

5. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
After preprocessing,
?!
!? ?
!?

6. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j

7. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
i
root

8. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
i
root

9. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
i
ancestors of node i
root

10. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
i
ancestors of node i
- nodes on the path
from i to the root
root

11. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j

12. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
j

13. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
j

14. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
j
ancestors of node j

15. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
j
ancestors of node j
- nodes on the path
from j to the root

16. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
j

17. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
i
j
root

18. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
i
j
rootcommon ancestors of i and j
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j

19. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
i
j
rootcommon ancestors of i and j
- nodes which are
ancestors of both i
and j
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j

20. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
i
j
root
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j

21. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
i
j
root
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
4
5
3
0
1
2

22. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
i
j
root
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
depth =
4
5
3
0
1
2

23. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
i
j
root
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
depth =lowest common ancestor of i and j
4
5
3
0
1
2

24. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
i
j
root depth =lowest common ancestor of i and j
- the common ancestor of i
and j furthest
from the root
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
4
5
3
0
1
2

25. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
4
5
3
0
1
2

26. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
i
j 4
5
3
0
1
2
LCA(i, j)

27. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
4
5
3
0
1
2

28. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
4
5
3
0
1
2
ij
LCA(i, j)

29. Lowest common ancestor
Preprocess a tree T (with n nodes) to answer lowest common ancestor queries. . .
After preprocessing,
the output to a query LCA(i, j) is the lowest common ancestor of nodes i and j
4
5
3
0
1
2
ij
LCA(i, j)
• Ideally, we would like O(n) space, O(n) prep. time and O(1) query time

30. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
7
0
9
6
1

31. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
the nodes are numbered between
0 and (n − 1)
7
0
9
6
1

32. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
7
0
9
6
1

33. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
Write down every node you visit
. . . and its depth
7
0
9
6
1

34. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
0(node) N
Write down every node you visit
. . . and its depth
(depth) D 0
7
0
9
6
1

35. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
10(node) N
Write down every node you visit
. . . and its depth
(depth) D 10
7
0
9
6
1

36. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 50(node) N
Write down every node you visit
. . . and its depth
(depth) D 210
7
0
9
6
1

37. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 50(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210
7
0
9
6
9
1

38. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 50(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2
7
0
9
6
9
1

39. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 100(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3
7
0
9
6
9
1

40. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 50(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2
7
0
9
6
9
1

41. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 10(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1
7
0
9
6
9
1

42. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 10(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2
7
0
9
6
9 6
1

43. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 10(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1
7
0
9
6
9 6
1

44. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 00(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1
7
0
0
9
6
9 6
1

45. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 20(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1
7
0
0
9
6
9 6
1

46. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 00(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0
7
0
0
9
6
9 6
1

47. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 30(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1
7
0
0
9
6
9 6
1

48. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 30(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2
7
7
0
0
9
6
9 6
1

49. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 30(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1
7
7
0
0
9
6
9 6
1

50. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 80(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2
7
7
0
0
9
6
9 6
1

51. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 30(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1
7
7
0
0
9
6
9 6
1

52. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 00(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0
7
7
0
0
9
6
9 6
1

53. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 40(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1
7
7
0
0
9
6
9 6
1

54. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
7
7
0
0
9
6
9 6
1

55. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
7
7
0
0
9
6
9 6
1

56. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
7
7
0
0
9
6
9 6
1

57. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1

58. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
how do we find LCA(i,j)?
7
i j
7
0
0
9
6
9 6
1

59. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
how do we find LCA(i,j)?
7
i j
Find i and j in N
7
0
0
9
6
9 6
1

60. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
how do we find LCA(i,j)?
7
i j
Find i and j in N
7
i j
0
0
9
6
9 6
1

61. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
how do we find LCA(i,j)?
7
i j
Find i and j in N
7
i j
Compute RMQ(i , j ) in D
0
0
9
6
9 6
1

62. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
how do we find LCA(i,j)?
7
i j
Find i and j in N
7
i j
Compute RMQ(i , j ) in D
0
0
9
6
9 6
1

63. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
9
6
9 6
1

64. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
ji
9
6
9 6
1

65. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
ji
9
6
Find i and j in N
9 6
1

66. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
ji
9
6
Find i and j in N
i j
9 6
1

67. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
ji
9
6
Find i and j in N
i j
Compute RMQ(i , j ) in D
9 6
1

68. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
ji
9
6
Find i and j in N
i j
Compute RMQ(i , j ) in D
9 6
1
11

69. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
9
6
9 6
1

70. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
9
6
9 6
1
ji

71. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
9
6
9 6
1
ji
Find i and j in N. . .

72. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
9
6
9 6
1
ji
Find i and j in N. . . which copy of i?

73. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
Compute an Euler tour of T. . .
(a depth first search with repeats)
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
How long is the tour?
We follow each edge twice. . .
and there are (n − 1) edges
Write down every node you visit
. . . and its depth
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
how do we find LCA(i,j)?
9
6
9 6
1
ji
Find i and j in N. . . which copy of i?
any copy is fine

74. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1

75. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i

76. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]

77. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)

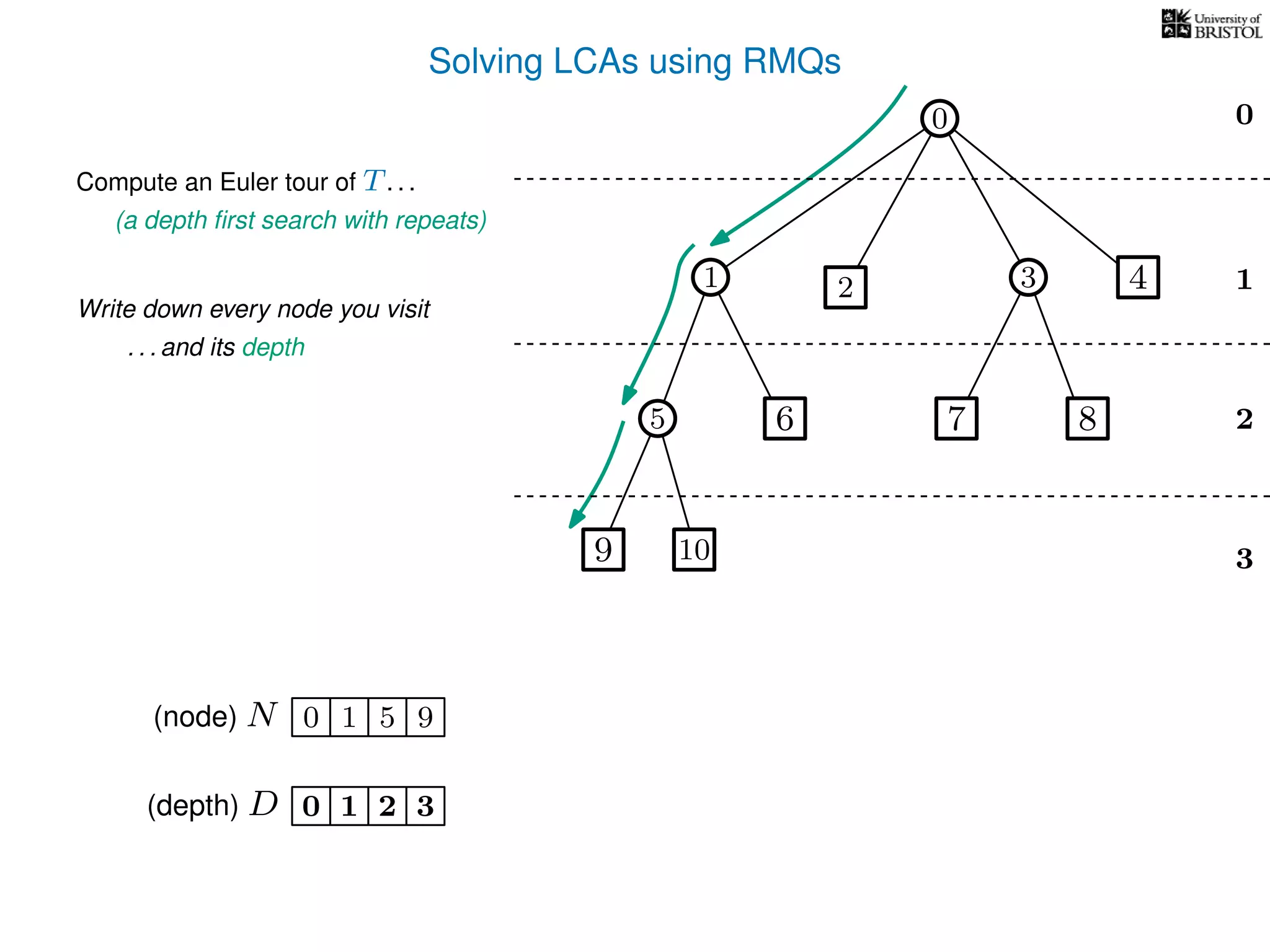
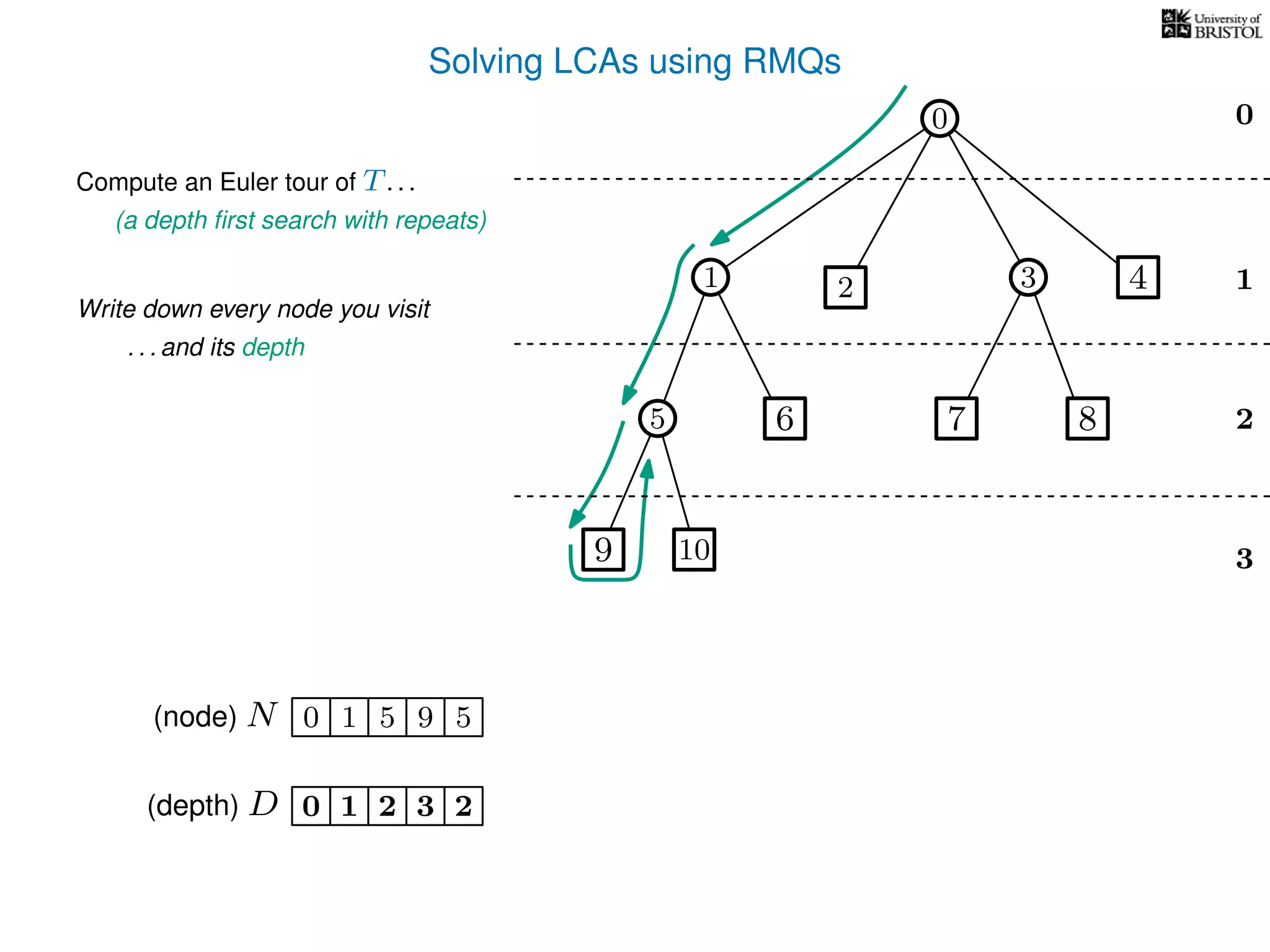
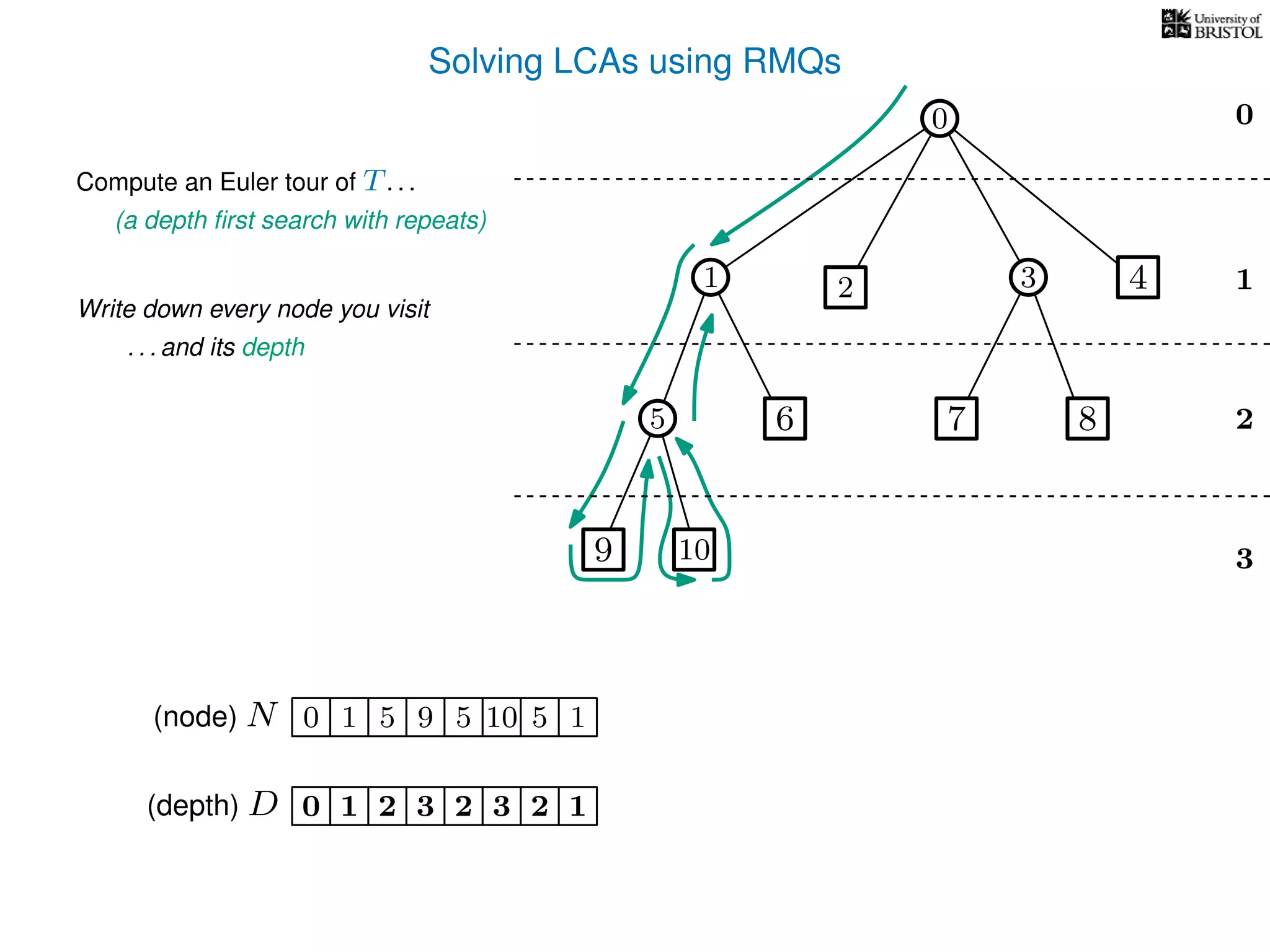
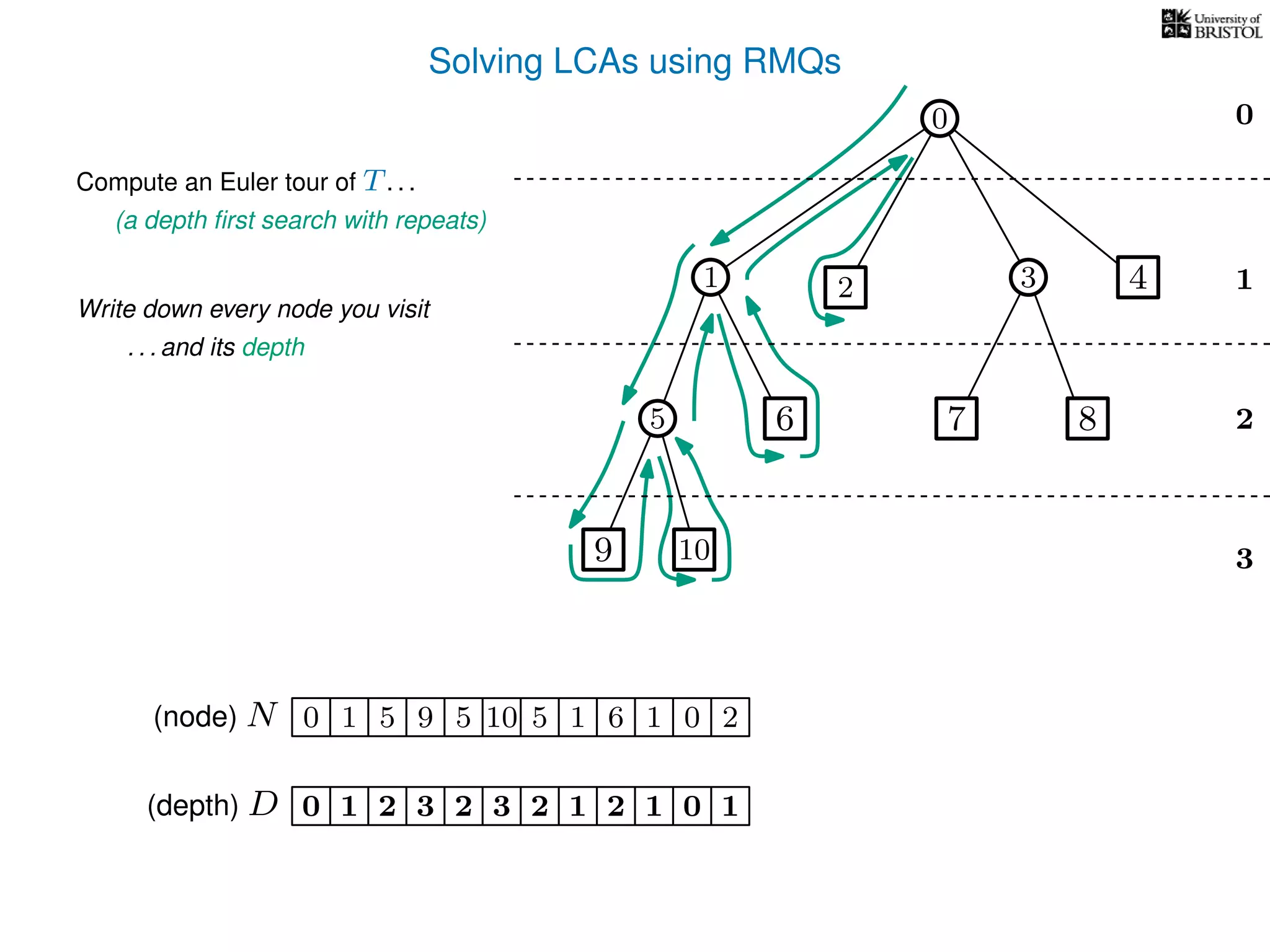
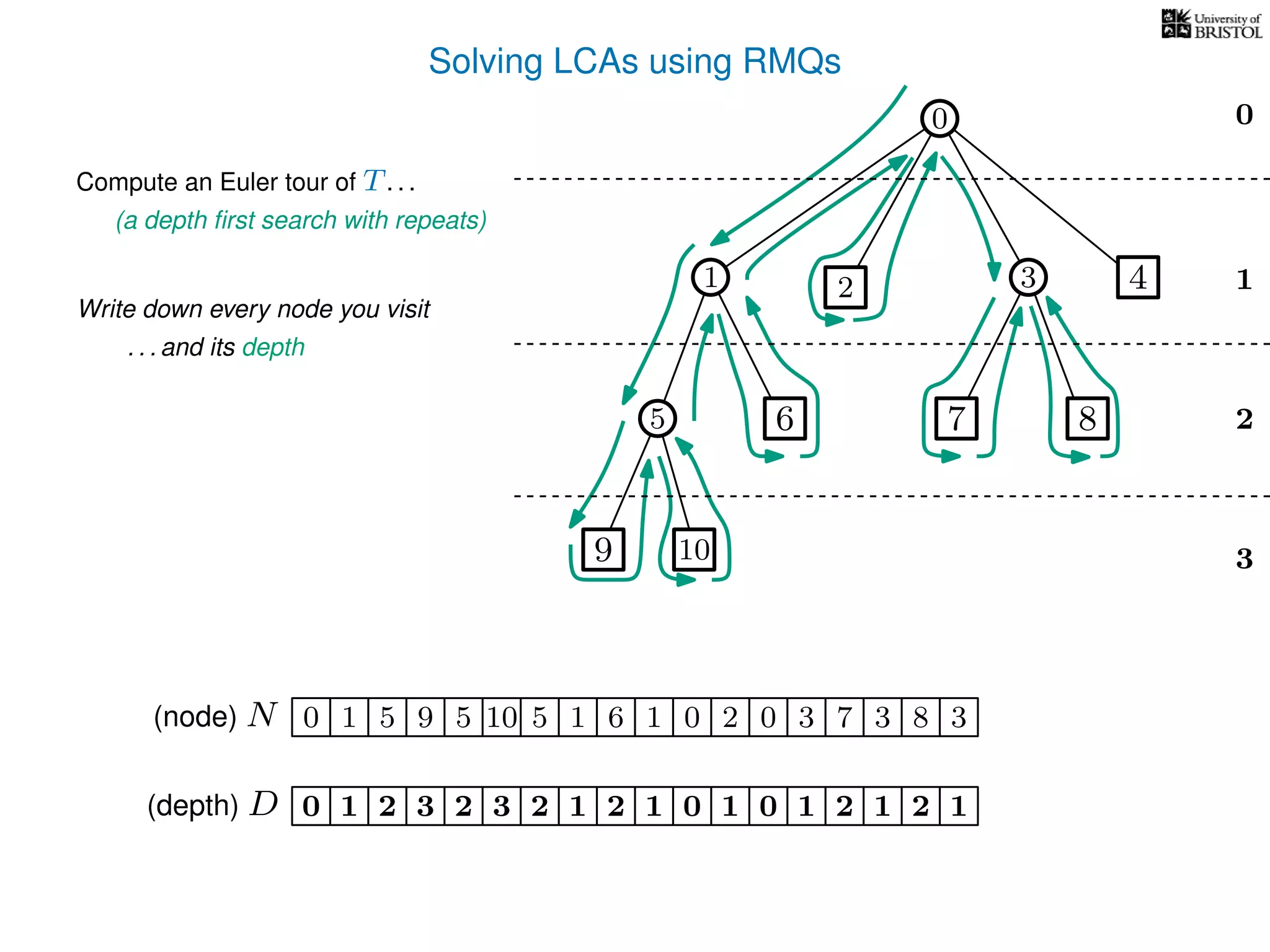
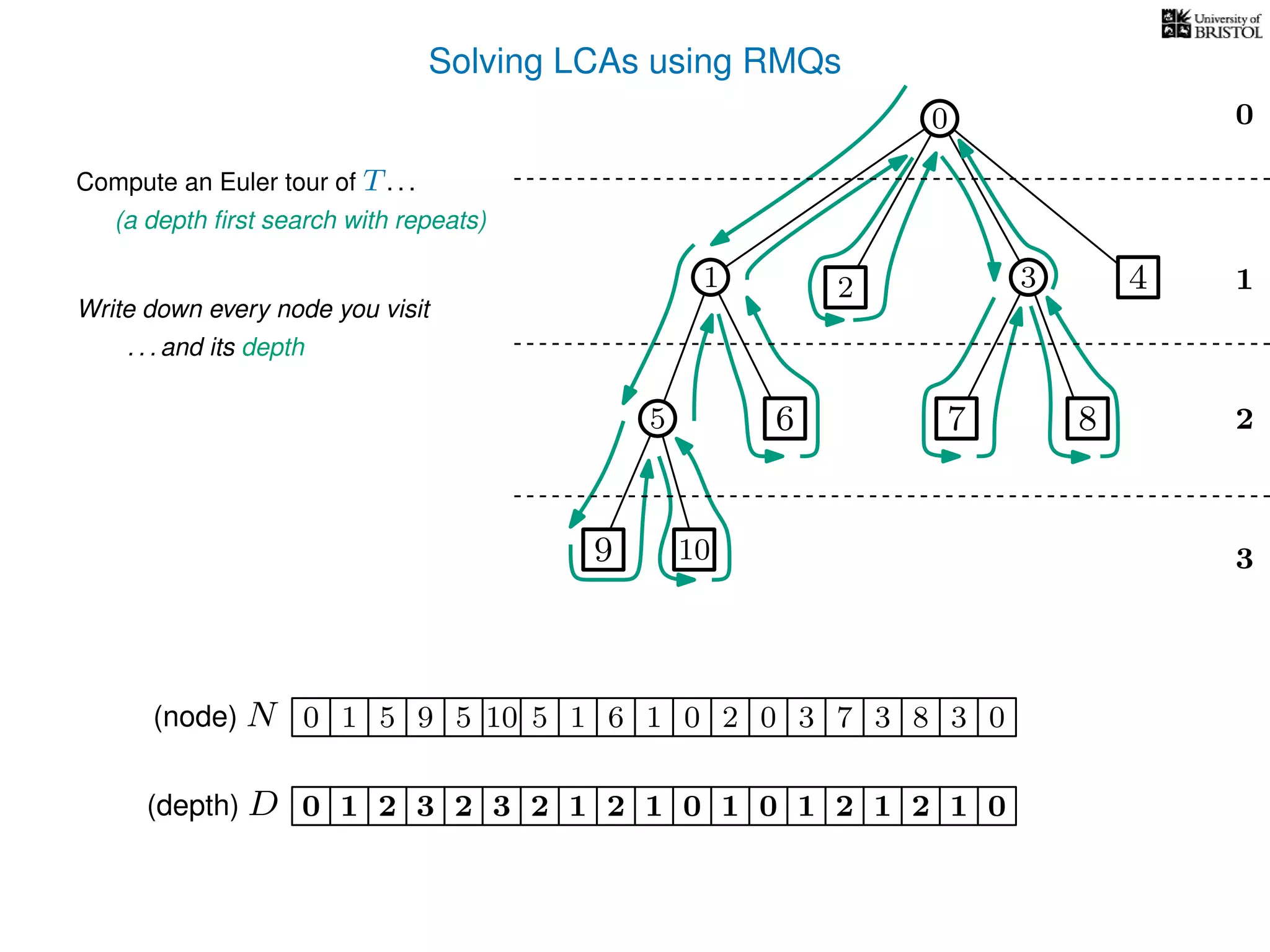
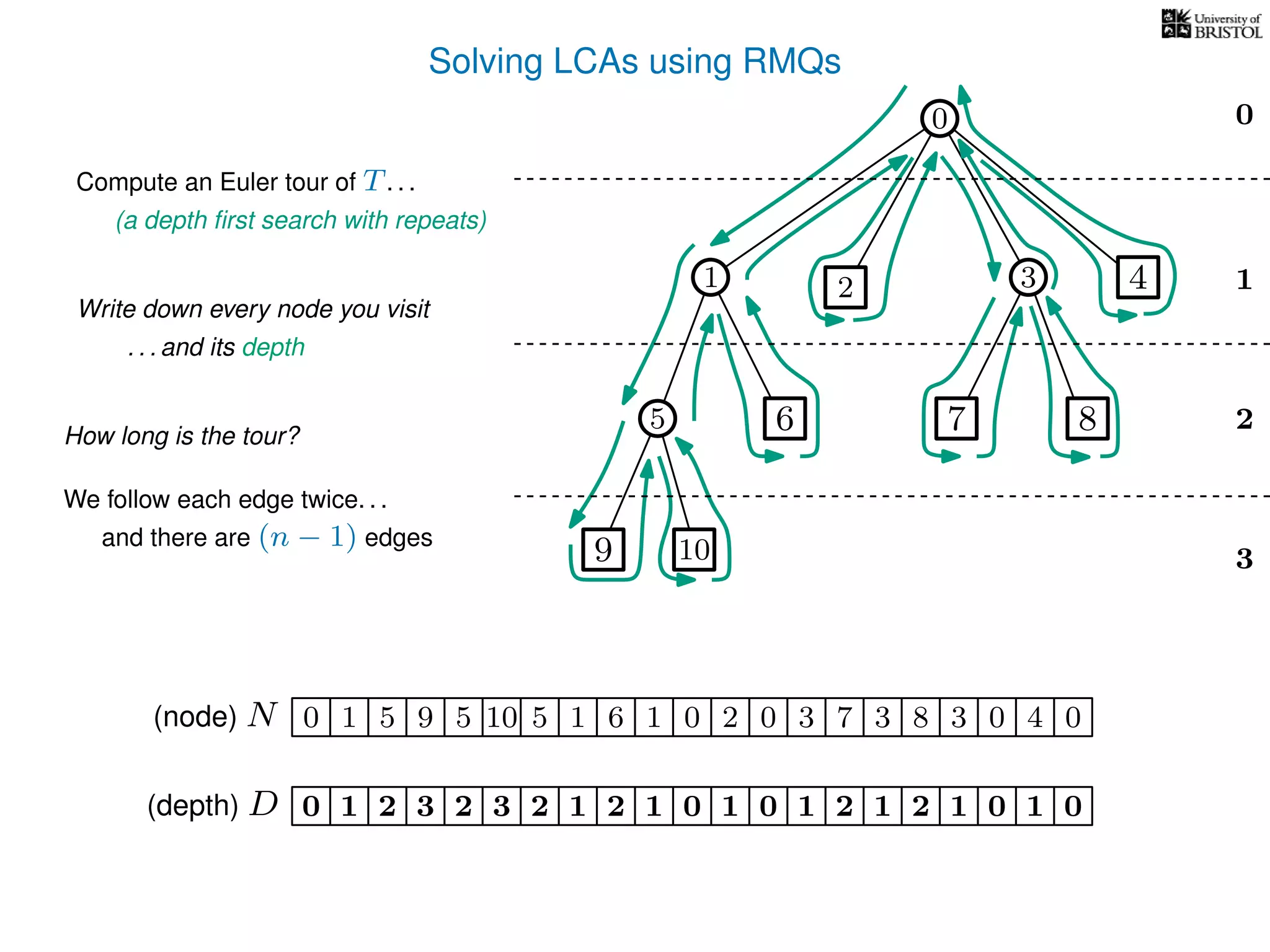
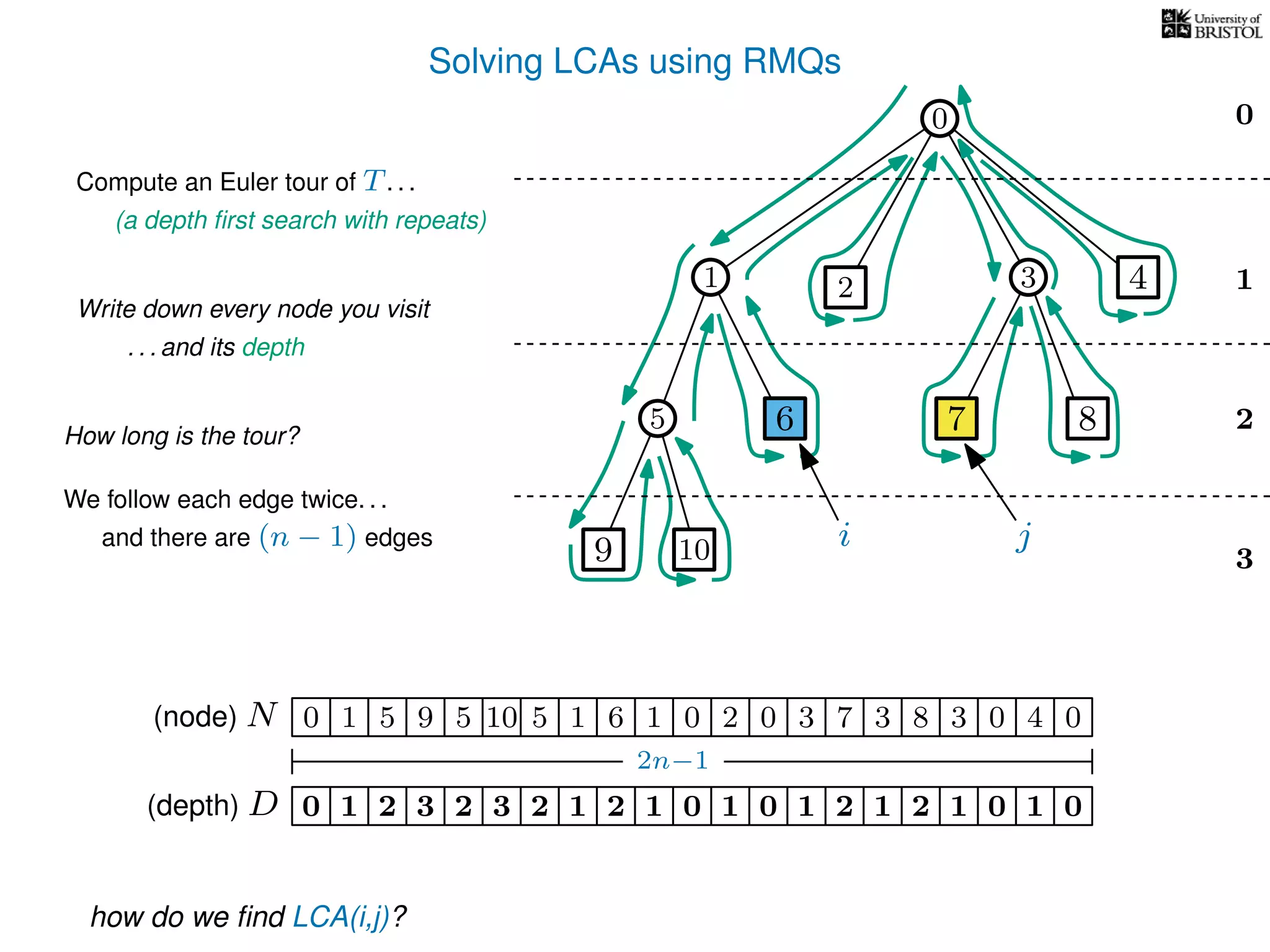
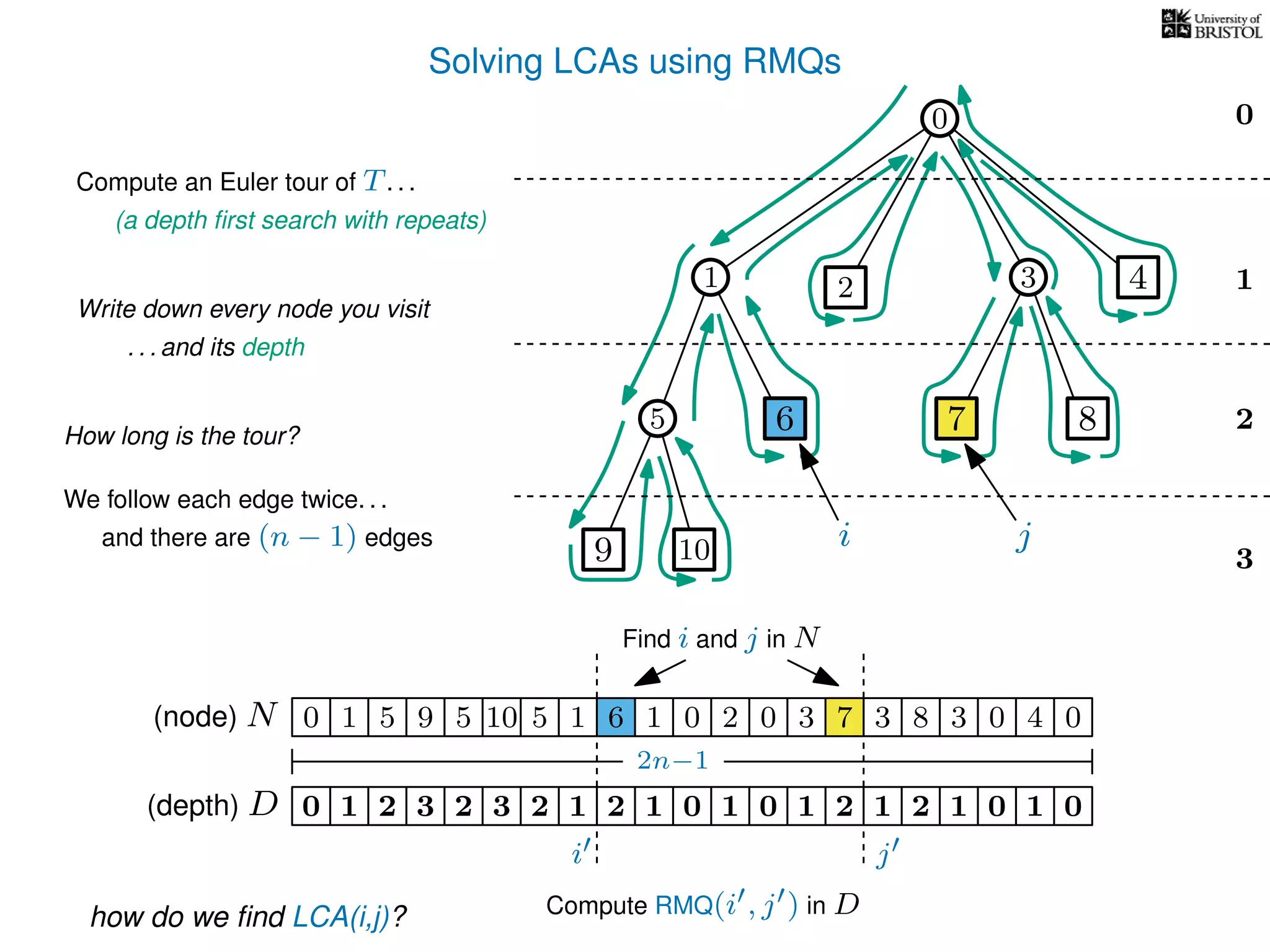
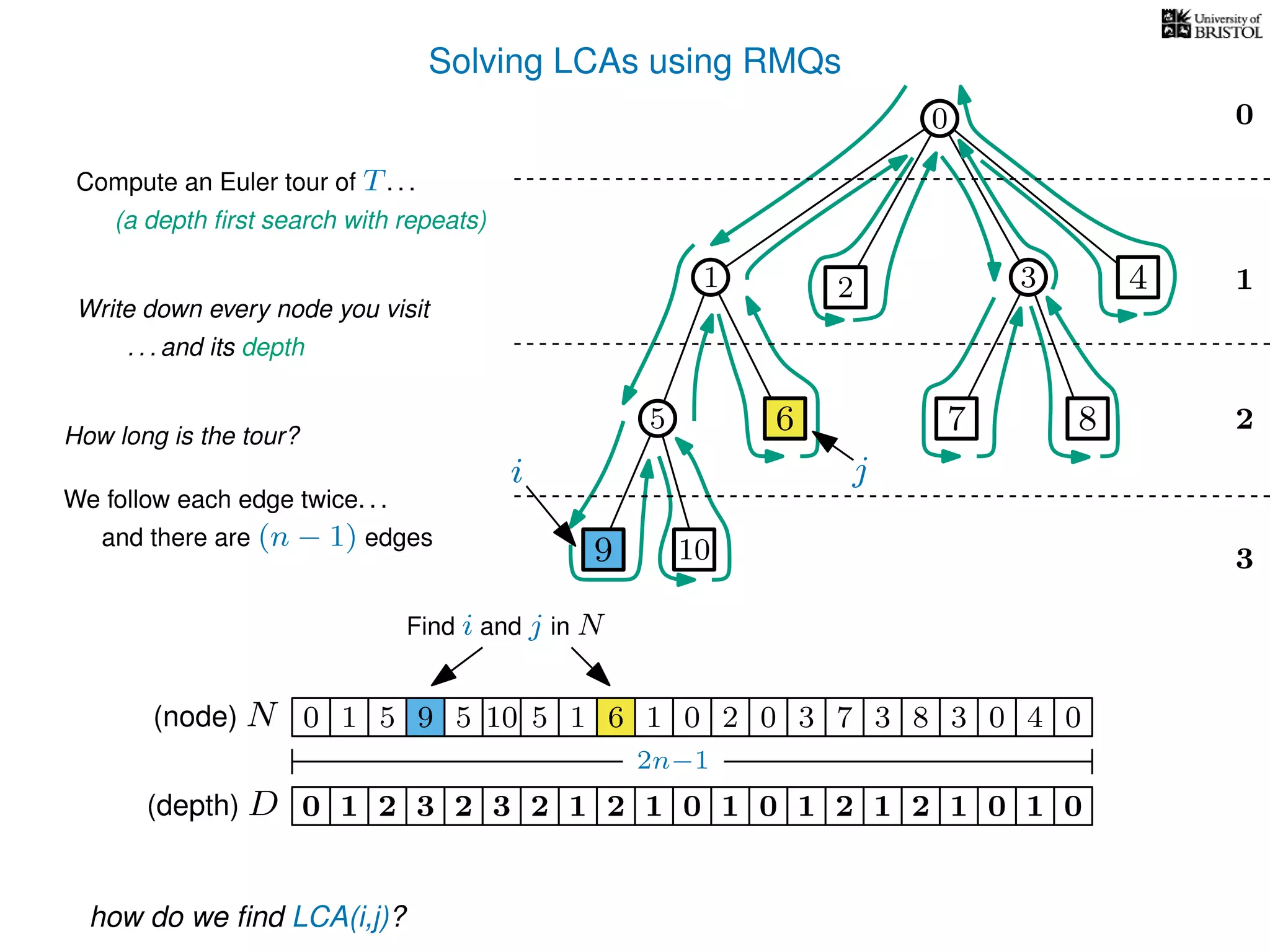
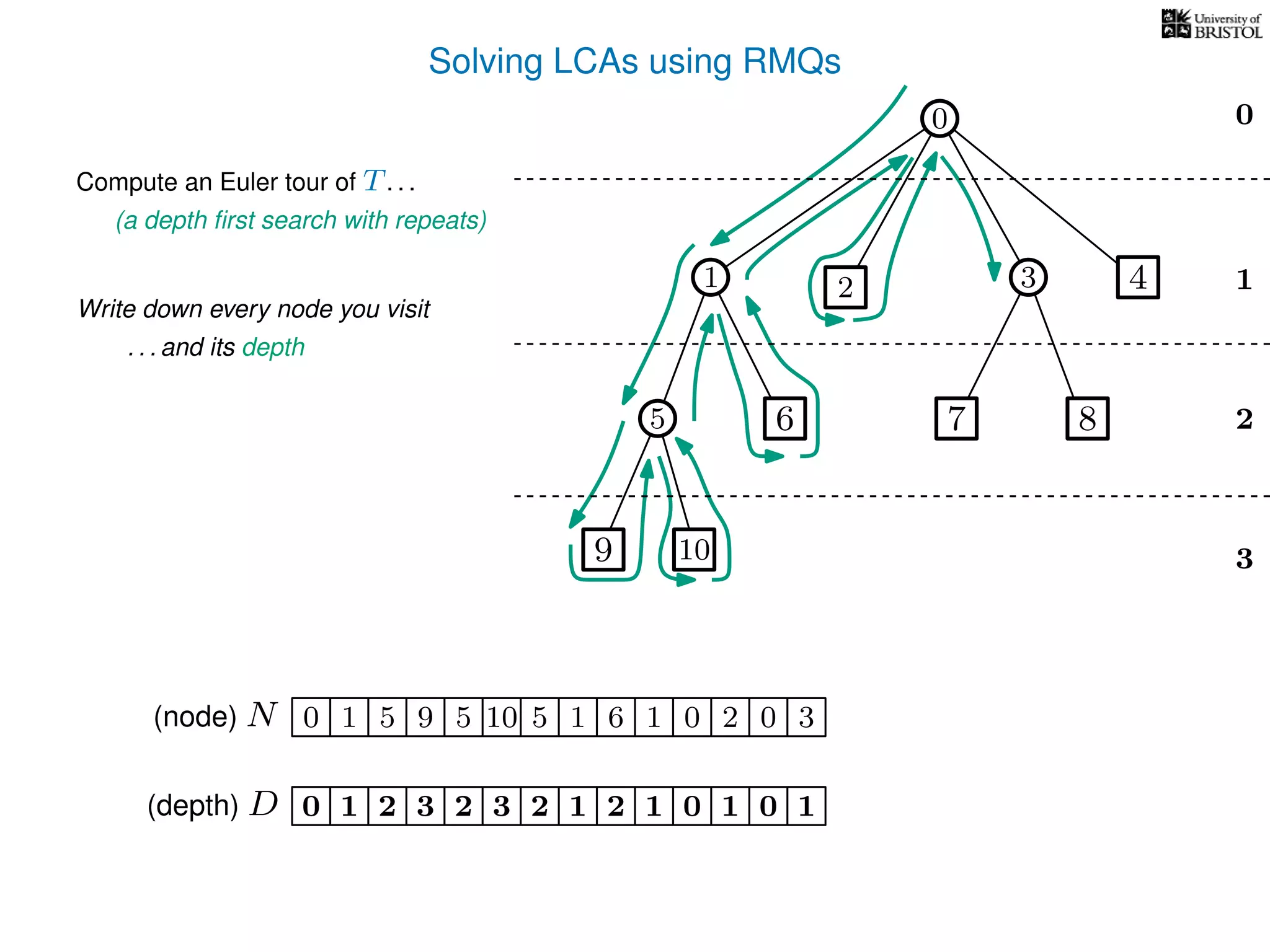
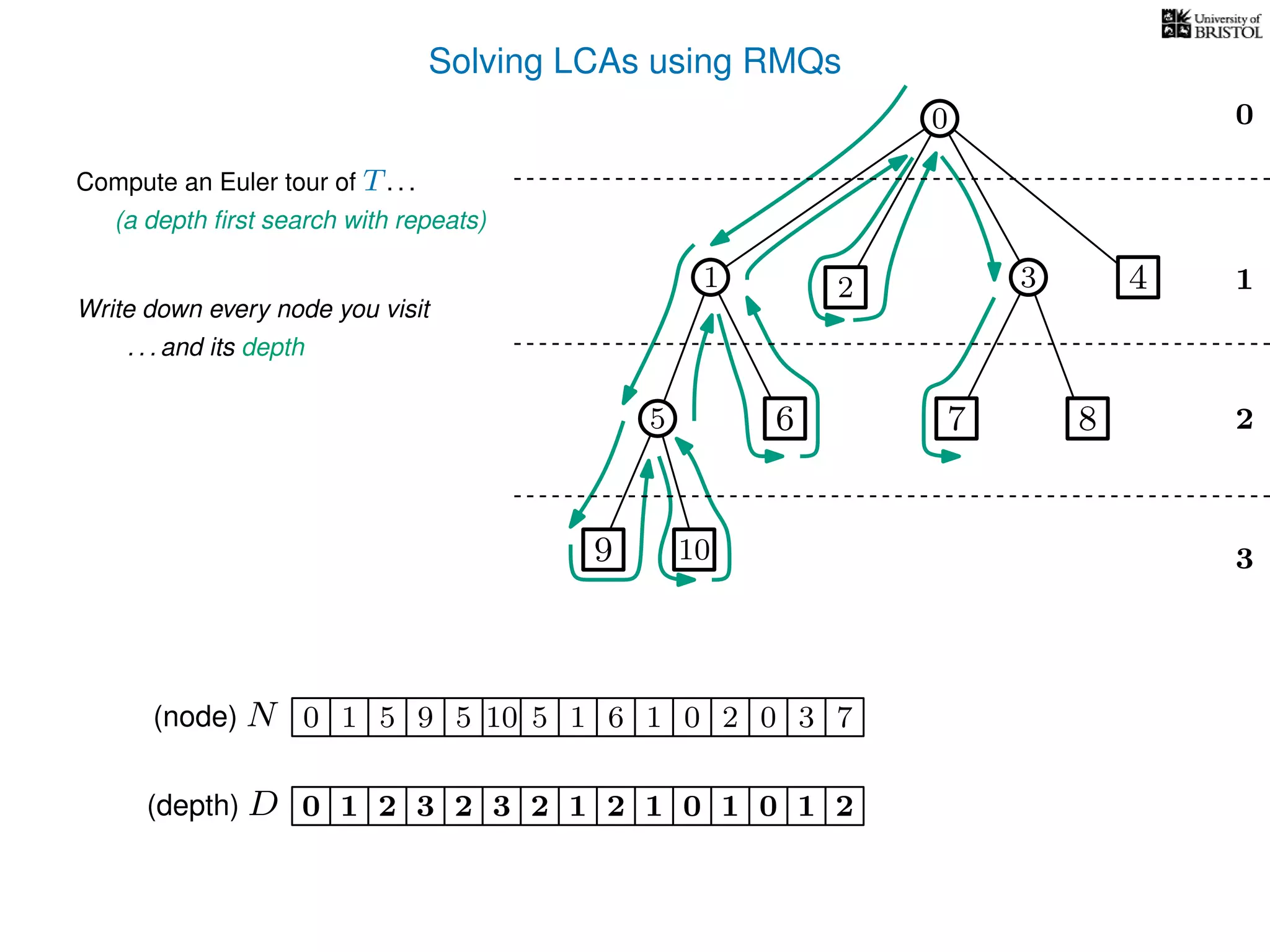
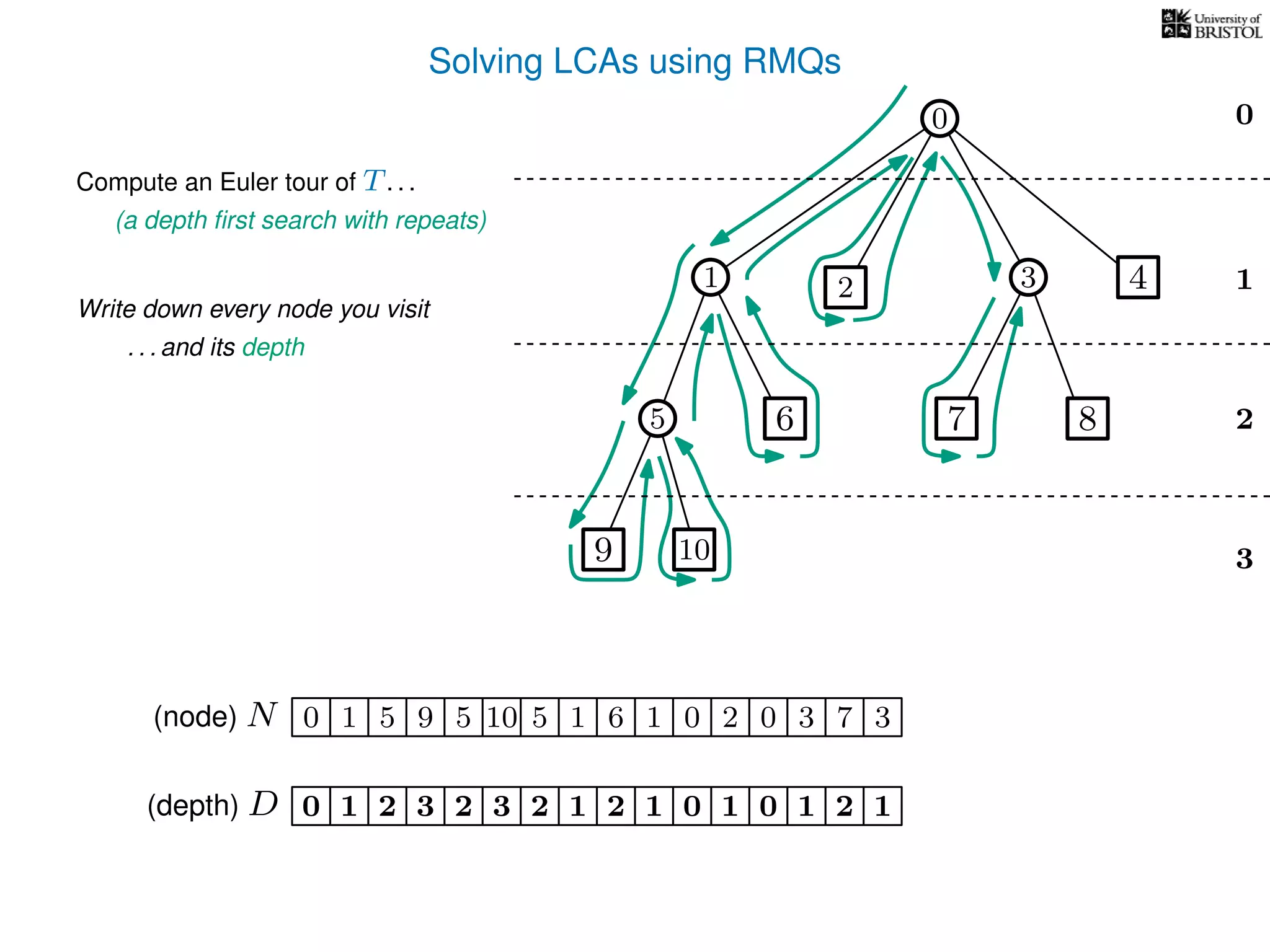
78. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(n)

79. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(n)
O(?)

80. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(?)

81. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(?)
O(1)

82. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(?)
O(1)
O(?)

83. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(?)
O(1)
O(?)
O(1)

84. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(?)
O(1)
O(?)
O(1)
Prep. time O(n + prepRMQ(n))
Query time O(1 + queryRMQ(n))
Space O(n + spaceRMQ(n))
depends on the RMQ structure used

85. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(?)
O(1)
O(?)
O(1)
Prep. time O(n log log n)
Query time O(1)
Space O(n log log n)
using the best result from last lecture

86. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
why does this work?
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(?)
O(1)
O(?)
O(1)
Prep. time O(n log log n)
Query time O(1)
Space O(n log log n)
using the best result from last lecture

87. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
depth > d + 1
S2
x

88. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
children
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
depth > d + 1
S2
x

89. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
subtrees
children
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
depth > d + 1
S2
x

90. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
subtrees
children
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
S2
x

91. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
S2
x

92. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
y yy y
d + 1 d + 1d + 1 d + 1
x
y

93. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
y yy y
d + 1 d + 1d + 1 d + 1
x
y

94. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
x
y

95. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
i j
x
y

96. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
i j imagine LCA(i, j) is not y
x
y

97. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
i j imagine LCA(i, j) is not y
i and j are in here so RMQ does not return the location of a y
x
y

98. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
i j imagine LCA(i, j) is not y
i and j are in here so RMQ does not return the location of a y
x
y
(all of the ys are out of range)

99. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
x
y

100. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
i
j
x
y

101. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
i
j
again, imagine LCA(i, j) is not y
x
y

102. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
i
j
again, imagine LCA(i, j) is not y
i and j cross an x (which has smaller depth than y)
so the RMQ location isn’t a y
x
y

103. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
x
y

104. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
x
i j
y

105. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
x
i j
y
now imagine LCA(i, j) is y

106. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
x
i j
y
now imagine LCA(i, j) is y
i and j cross a y (which is the smallest in the range)

107. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
x
i j
y
now imagine LCA(i, j) is y
i and j cross a y (which is the smallest in the range)

108. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
x
i j
y
now imagine LCA(i, j) is y
i and j cross a y (which is the smallest in the range)

109. Solving LCA using RMQ - correctness
We can also define a Euler tour of T recursively. . .
S1 S3 Sk
depth = d
depth = d + 1
x x xx(node) N
(depth) D
x x
d d dd d d
tour of S1 tour of S2 tour of S3 tour of Sk
depth > d + 1
Claim the RMQ reports the location of
some y in N iff LCA(i, j) = y
y yy y
d + 1 d + 1d + 1 d + 1
x
i j
y
now imagine LCA(i, j) is y
i and j cross a y (which is the smallest in the range)
so the RMQ reports a y

110. Ongoing Summary
We have seen an O(n log log n) space, O(n log log n) prep. time and O(1) query time solution
for the Lowest Common Ancestor problem
which uses solution 3 for RMQ from last lecture

111. Ongoing Summary
Can we do better?
We have seen an O(n log log n) space, O(n log log n) prep. time and O(1) query time solution
for the Lowest Common Ancestor problem
which uses solution 3 for RMQ from last lecture

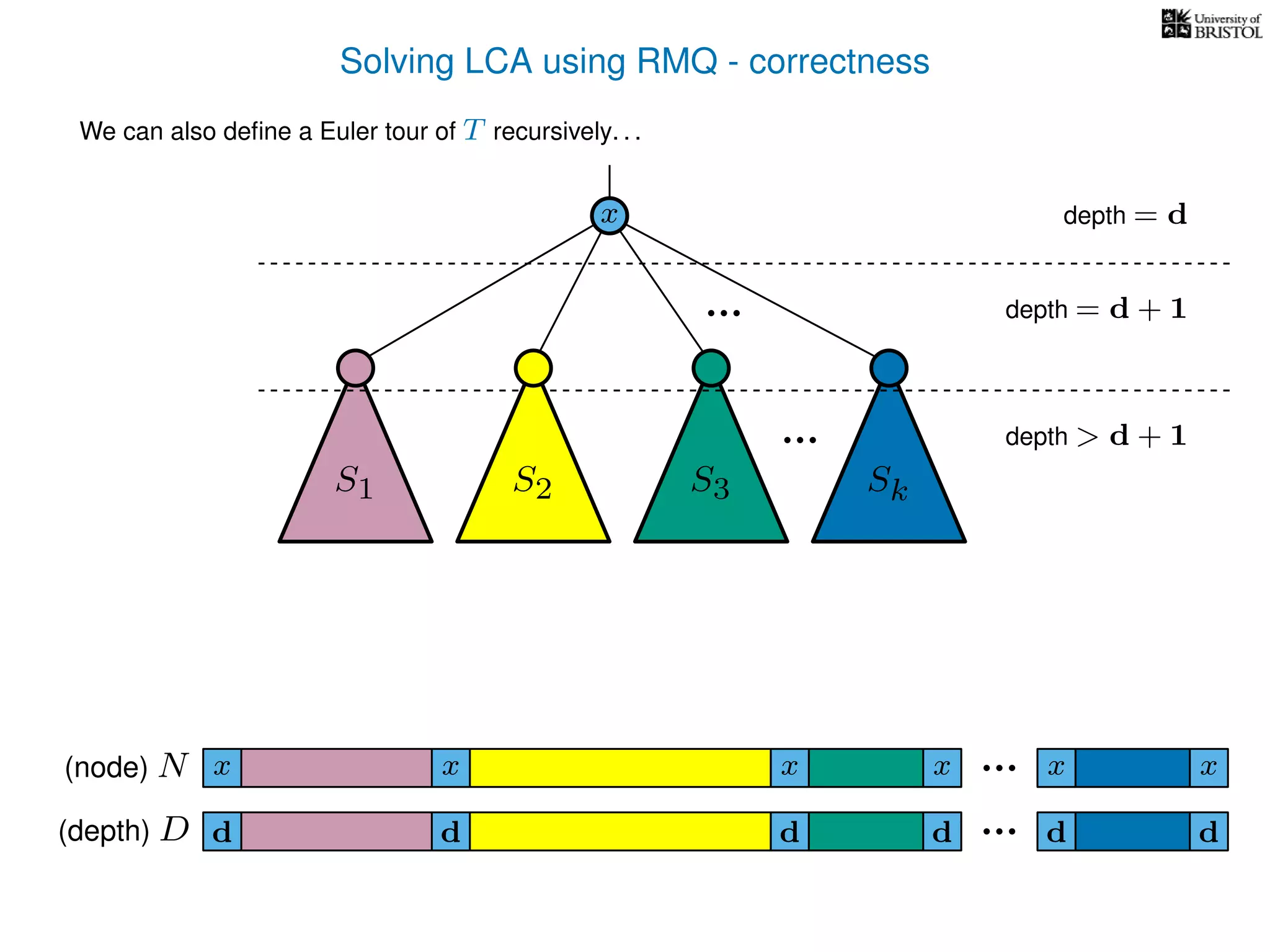
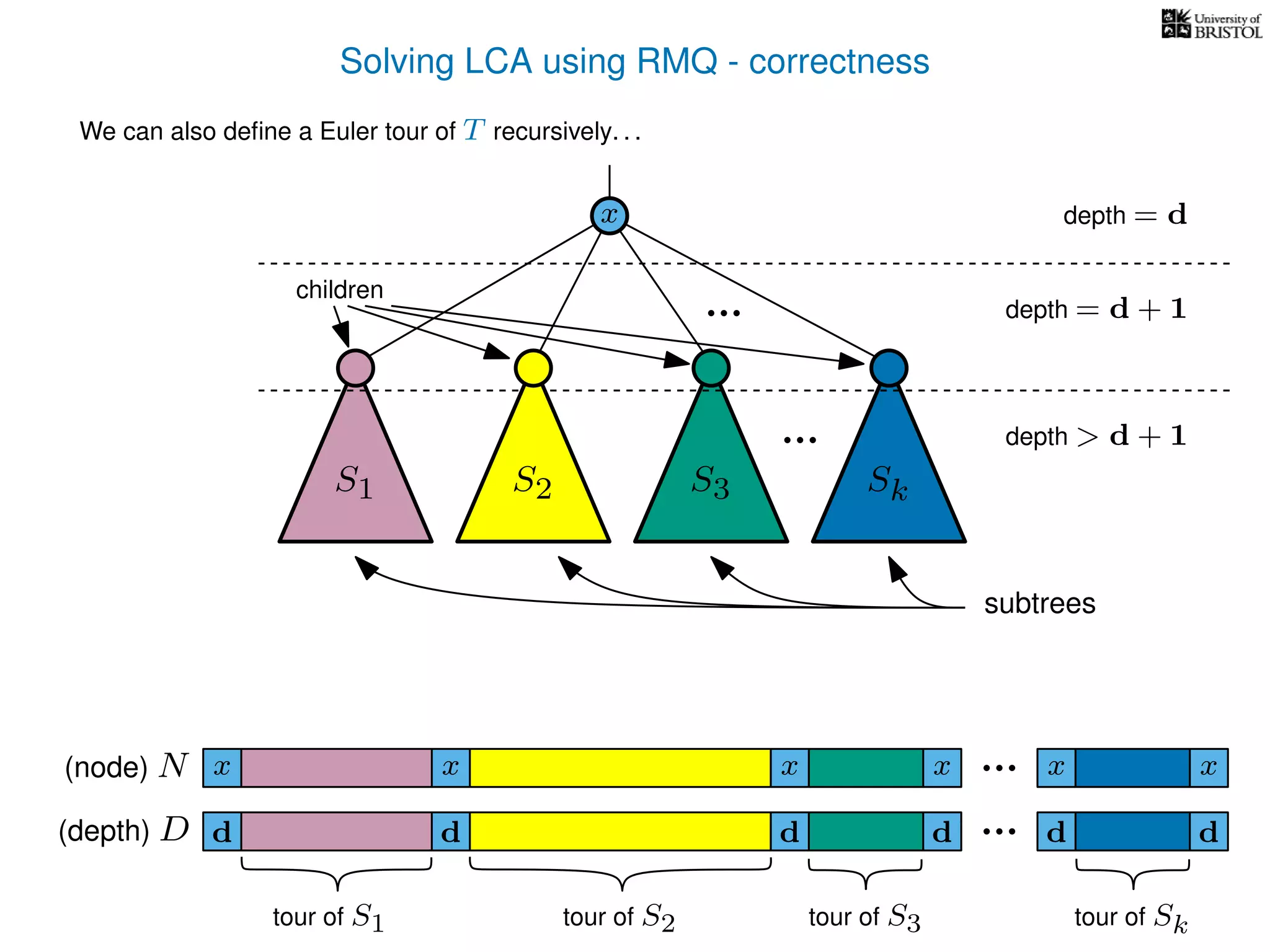
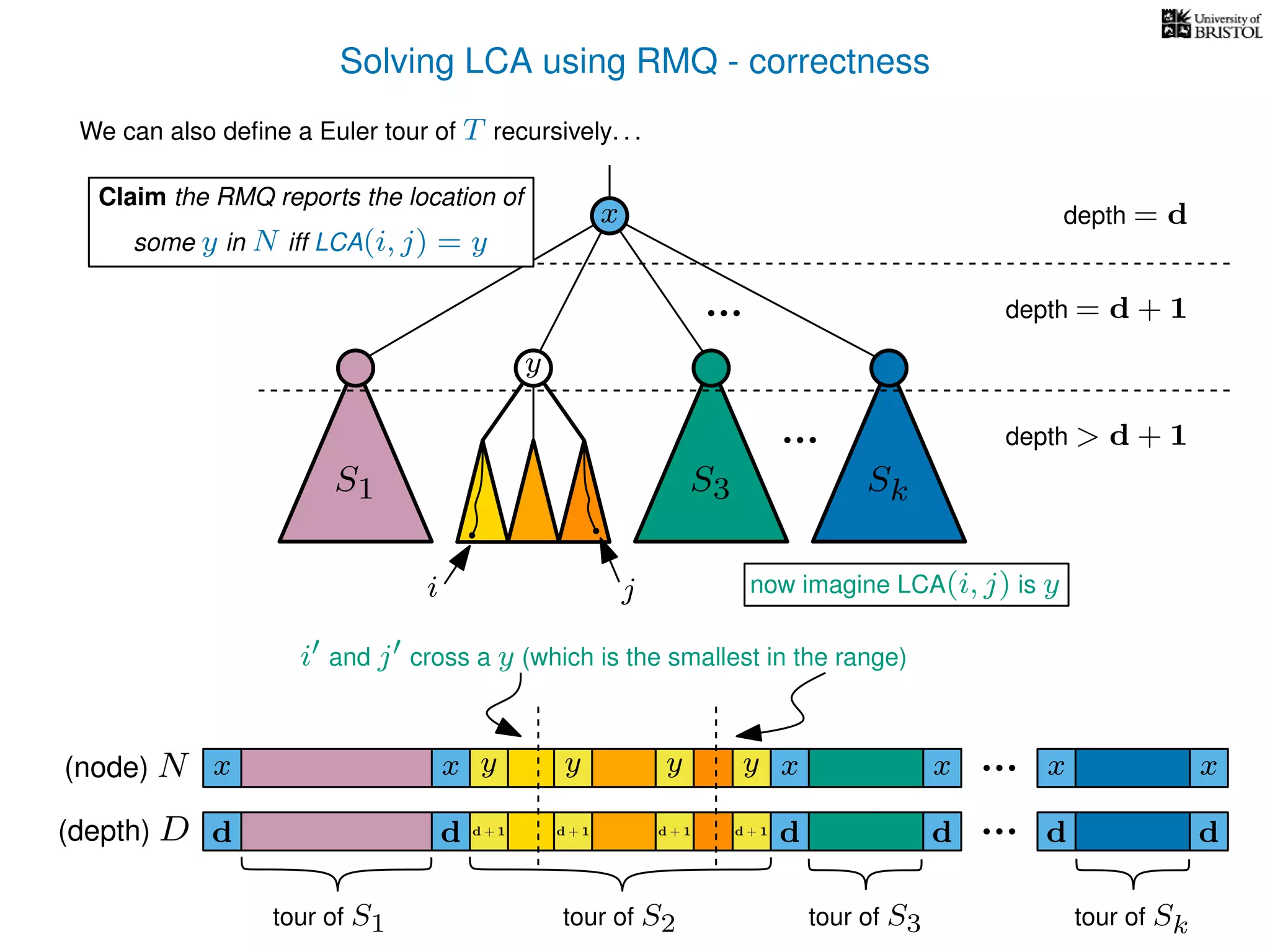
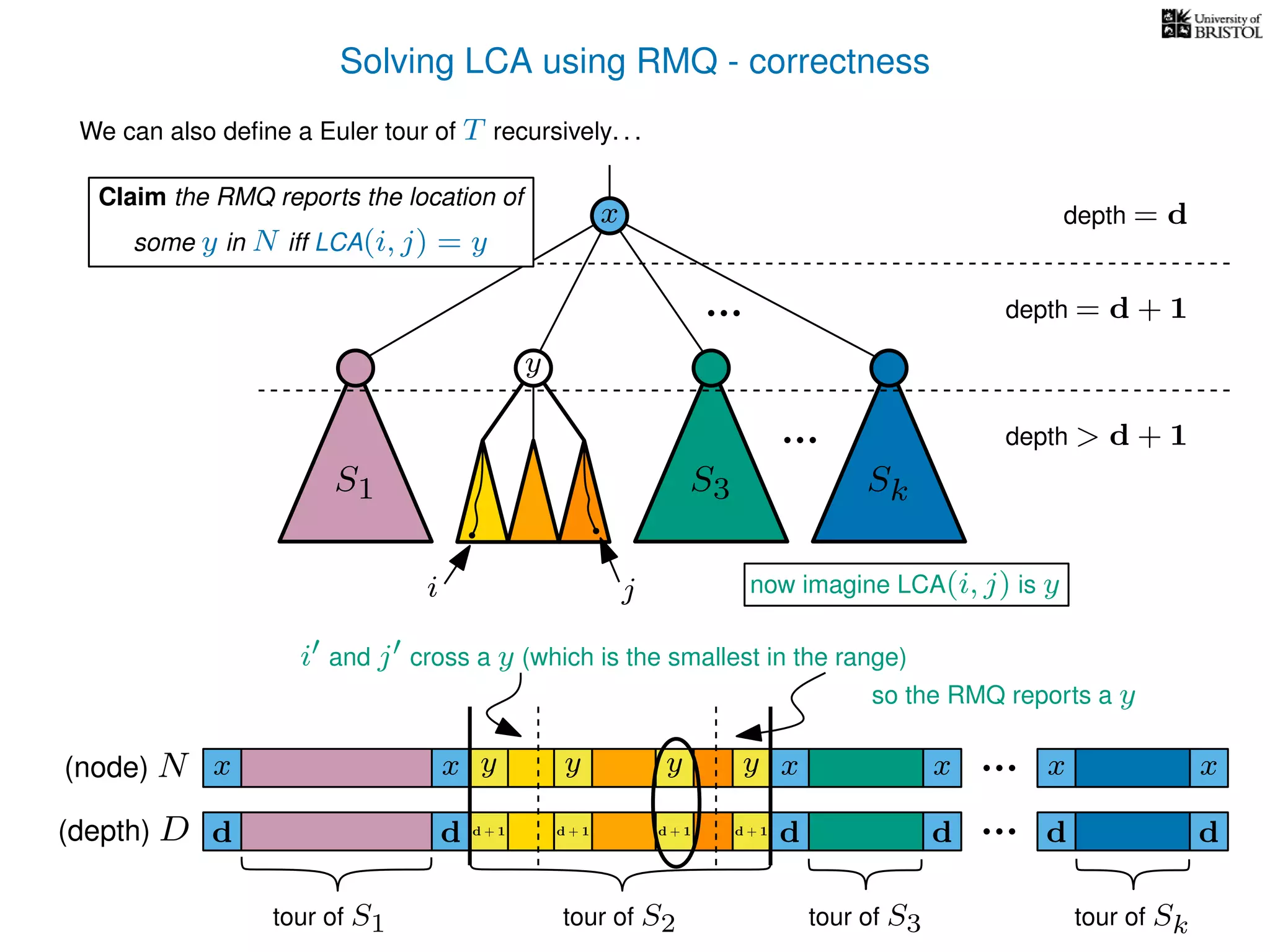
112. Solving LCAs using RMQs - efficiency
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]

113. Solving LCAs using RMQs - efficiency
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
Notice anything interesting about D?
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]

114. Solving LCAs using RMQs - efficiency
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
Notice anything interesting about D? D[i + 1] = D[i] ± 1
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]

115. ±1 Range minimum query
A
Preprocess an integer array A (length n) to answer range minimum queries. . .
n
After preprocessing, a range minimum query is given by RMQ(i, j)
the output is the location of the smallest element in A[i, j]
e.g. RMQ(3, 7) = 5, which is the location of the smallest element in A[3, 7]
i = 3 j = 7
RMQ(3, 7) = 5
• Can we exploit this ±1 property to get a more efficient RMQ data structure?
• Ideally we would like O(n) space, O(n) prep. time and O(1) query time
where for all k, we have A[k + 1] = A[k] ± 1
16 1715 16 15 14 15 16 17 18 19 20 21 20 19 20
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
(in a tie, report the leftmost)

116. Low-resolution RMQ (again)
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
i j
Preprocess the array H which has length ˜n = 2n
log n to answer RMQs. . .
in O(n) space/prep time
Preprocess each array Li (which has length (log n)/2) to answer RMQs. . .
in O(log n log log n) space/prep time
How do we answer a query in A in O(1) time?
Do one query in H and one query in two different Li and return the smallest
˜n = 2n
log n
log n
2
min of these
as there are O(n/ log n) Li arrays, we have O(n log log n) total space/prep time
L0
L1
L2
L3
L4
L5 L˜n
goes in here
all of these
go in here

117. Low-resolution RMQ (again)
A
Key Idea replace A with a smaller, ‘low resolution’ array H
H
˜n
i j
and many small arrays L0, L1, L2 . . . ‘for the details’
n
i j
Preprocess the array H which has length ˜n = 2n
log n to answer RMQs. . .
in O(n) space/prep time
Preprocess each array Li (which has length (log n)/2) to answer RMQs. . .
in O(log n log log n) space/prep time
How do we answer a query in A in O(1) time?
Do one query in H and one query in two different Li and return the smallest
˜n = 2n
log n
log n
2
min of these
as there are O(n/ log n) Li arrays, we have O(n log log n) total space/prep time
too big and slow!
L0
L1
L2
L3
L4
L5 L˜n
goes in here
all of these
go in here

118. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?

119. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to

120. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
(remember these are the locations of the minimum)

121. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
(remember these are the locations of the minimum)

122. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
RMQx(0, 2) = RMQy(0, 2) = 2
RMQx(3, 4) = RMQy(3, 4) = 4
RMQx(0, 4) = RMQy(0, 4) = 2
RMQx(0, 1) = RMQy(0, 1) = 1
(remember these are the locations of the minimum)

123. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
(remember these are the locations of the minimum)

124. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
(remember these are the locations of the minimum)

125. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
0100 0100
(remember these are the locations of the minimum)

126. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
0100 0100
(remember these are the locations of the minimum)

127. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
0100 0100dx = dy == 2 = 2
(remember these are the locations of the minimum)

128. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
Fact Lx is equivalent to Ly
iff dx = dy
0100 0100dx = dy == 2 = 2
(remember these are the locations of the minimum)

129. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
Fact Lx is equivalent to Ly
• We can precompute dx for each Lx in O(|Lx|) = O(log n) time.
iff dx = dy
0100 0100dx = dy == 2 = 2
(remember these are the locations of the minimum)

130. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
Fact Lx is equivalent to Ly
• We can precompute dx for each Lx in O(|Lx|) = O(log n) time.
• How many different values of d are there?
iff dx = dy
0100 0100dx = dy == 2 = 2
(remember these are the locations of the minimum)

131. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
Fact Lx is equivalent to Ly
• We can precompute dx for each Lx in O(|Lx|) = O(log n) time.
• How many different values of d are there?
iff dx = dy
0100 0100dx = dy == 2 = 2
d contains (log n)/2 − 1 bits so . . .
(remember these are the locations of the minimum)

132. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
Fact Lx is equivalent to Ly
• We can precompute dx for each Lx in O(|Lx|) = O(log n) time.
• How many different values of d are there?
iff dx = dy
0100 0100dx = dy == 2 = 2
d contains (log n)/2 − 1 bits so . . . at most 2(log n)/2
(remember these are the locations of the minimum)

133. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
Fact Lx is equivalent to Ly
• We can precompute dx for each Lx in O(|Lx|) = O(log n) time.
• How many different values of d are there?
iff dx = dy
0100 0100dx = dy == 2 = 2
d contains (log n)/2 − 1 bits so . . . at most 2(log n)/2 = 2log n
1/2
(remember these are the locations of the minimum)

134. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
Fact Lx is equivalent to Ly
• We can precompute dx for each Lx in O(|Lx|) = O(log n) time.
• How many different values of d are there?
iff dx = dy
0100 0100dx = dy == 2 = 2
d contains (log n)/2 − 1 bits so . . . at most 2(log n)/2 = 2log n
1/2 √
n
(remember these are the locations of the minimum)

135. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
Fact Lx is equivalent to Ly
• We can precompute dx for each Lx in O(|Lx|) = O(log n) time.
• How many different values of d are there?
• For each value of d we store RMQ(i, j) for all i, j
iff dx = dy
0100 0100dx = dy == 2 = 2
d contains (log n)/2 − 1 bits so . . . at most 2(log n)/2 = 2log n
1/2 √
n
(remember these are the locations of the minimum)

136. Counting ±1 RMQ arrays
L
log n
2
How many different ±1 RMQ arrays like this. . . are there?
Ly
log n
2
We say that iff for all (i, j): RMQx(i, j) = RMQy(i, j)
Lx
log n
2
is equivalent to
16 15 14 15 14 10 9 8 9 8is equivalent to
Lx Ly
0 1 2 3 4 0 1 2 3 4
16 15 14 15 14 10 9 8 9 8
0 1 2 3 4 0 1 2 3 4
Fact Lx is equivalent to Ly
• We can precompute dx for each Lx in O(|Lx|) = O(log n) time.
• How many different values of d are there?
• For each value of d we store RMQ(i, j) for all i, j
iff dx = dy
. . . this requires O(
√
n log2 n) = O(n) total space and prep. time
0100 0100dx = dy == 2 = 2
d contains (log n)/2 − 1 bits so . . . at most 2(log n)/2 = 2log n
1/2 √
n
(remember these are the locations of the minimum)

137. RMQ on the L arrays in linear space
A
Key Idea replace A with a smaller, ‘low resolution’ array H
n
˜n = 2n
log n
log n
2
L0
L1
L2
L3
L4
L5 L˜n
d0 d1 d2 d3 d4 d5 d˜n
precompute the value of dx for each Lx
in O(n) total space and prep. time
Precompute all the RMQ answers for
every value 0 d
√
n
in O(n) total space and prep. time
To perform a query within some Lx
• Look up dx
• Find the row dx in the table
• Find the entry giving RMQx(i, j)
row d3
This takes O(1) time

138. Optimal ±1 RMQ
Key Idea replace A with a smaller, ‘low resolution’ array H
and many small arrays L0, L1, L2 . . . ‘for the details’
Preprocess the array H (which has length ˜n = 8n
log n ) to answer RMQs. . .
in O(n) space/prep time
Preprocess each array Li (which has length (log n)/2) to answer RMQs. . .
in O(log n) space/prep time
How do we answer a query in A in O(1) time?
Do one query in H and one query in two different Li and return the smallest
˜n = 2n
log n
as there are O(n/ log n) Li arrays, we have O(n) total space/prep time
A
H
˜n
i j
n
i j
log n
2
min of these
L0
L1
L2
L3
L4
L5 L˜n
goes in here
all of these
go in here

139. Ongoing Summary
for the Lowest Common Ancestor problem
We have seen an O(n) space, O(n) prep. time and O(1) query time solution
for the ±1 Range Minimum Query problem
which improves solution 3 for RMQ from last lecture
(but only for ±1 inputs)
which uses solution 3 for RMQ from last lecture
We have seen an O(n log log n) space, O(n log log n) prep. time and O(1) query time solution

140. Ongoing Summary
How does this affect our LCA solution?
for the Lowest Common Ancestor problem
We have seen an O(n) space, O(n) prep. time and O(1) query time solution
for the ±1 Range Minimum Query problem
which improves solution 3 for RMQ from last lecture
(but only for ±1 inputs)
which uses solution 3 for RMQ from last lecture
We have seen an O(n log log n) space, O(n log log n) prep. time and O(1) query time solution

141. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(n)
O(1)
O(1)
O(1)

142. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(n)
O(1)
O(1)
O(1)

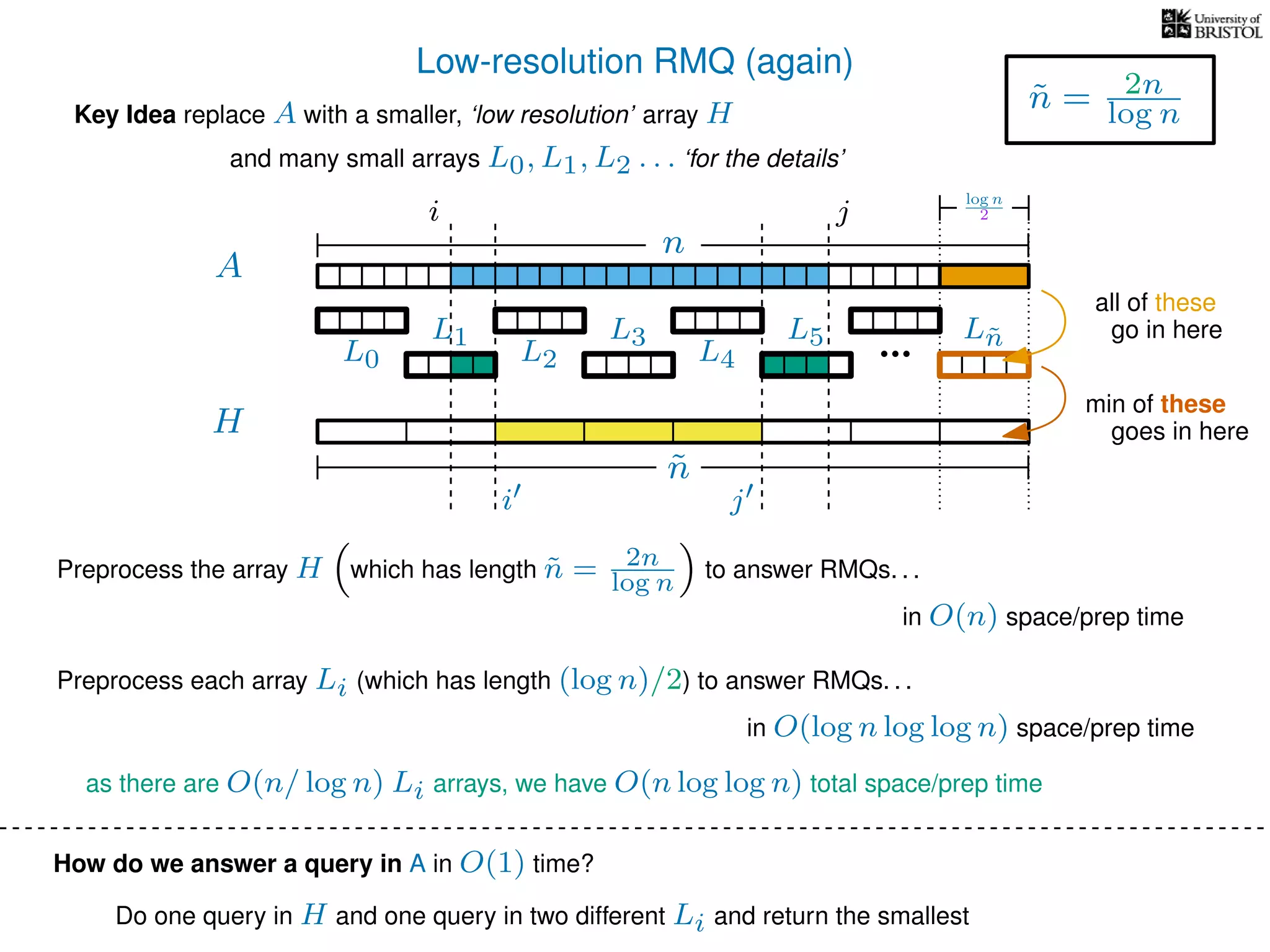
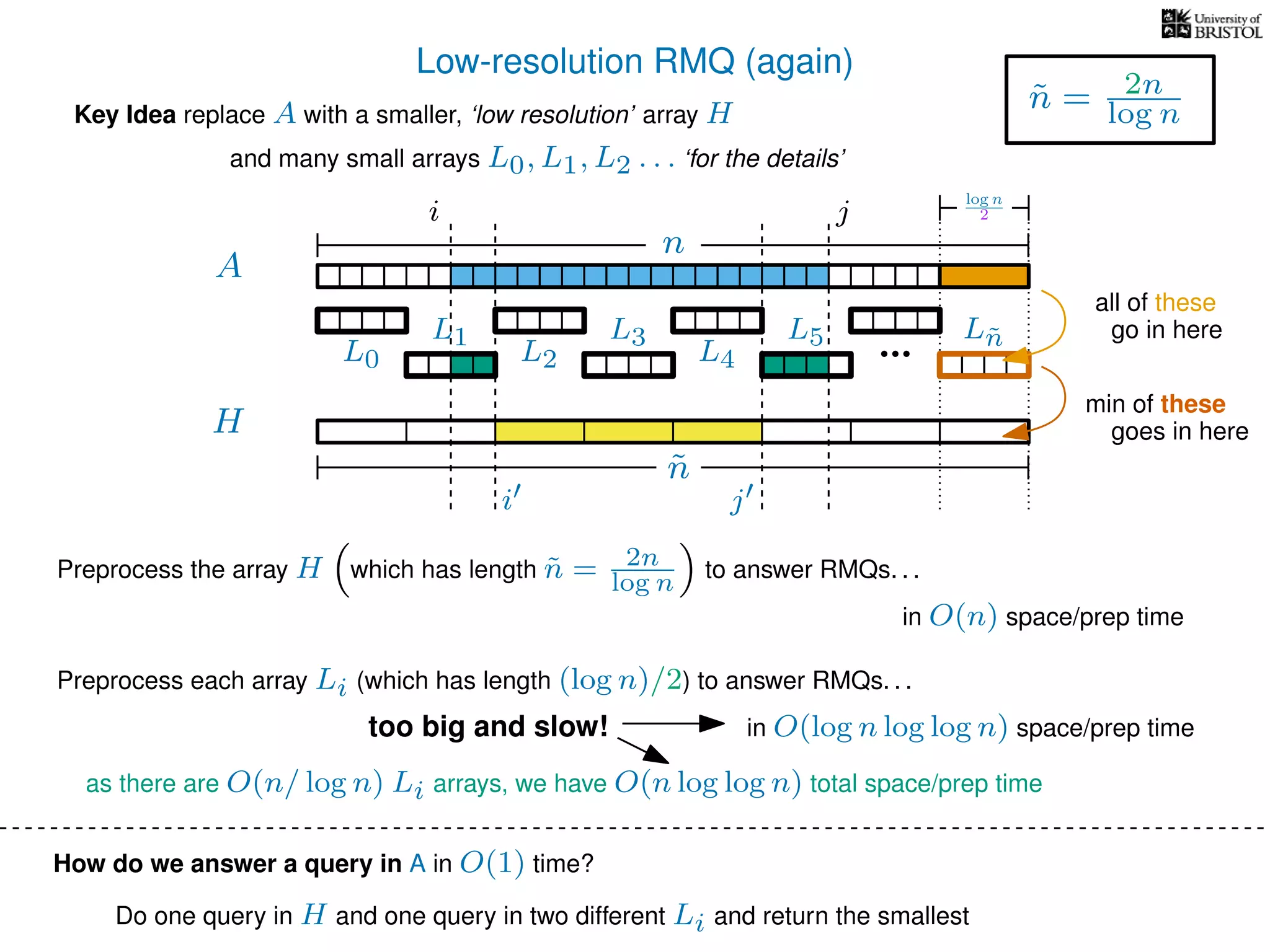
143. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(n)
O(1)
O(1)
O(1)
This gives us O(n) space, O(n) prep. time and O(1) query time
for the LCA problem

144. Solving LCAs using RMQs
3
0
1
2
2 3 4
5 8
10
1 5 5 10 5 1 1 0 2 0 3 3 8 3 0 4 00(node) N
(depth) D 3210 2 3 2 1 2 1 1 0 1 2 1 2 1 0 1 0
2n−1
7
7
0
0
9
6
9 6
1
Preprocessing Summary
1. Construct N and D from T
2. Add a pointer from each
3. Preprocess D for RMQs
node i to some N[i ] = i
Query Summary - LCA(i,j)
1. Find (any) i st. N[i ] = i
2. Find (any) j st. N[j ] = j
3. Compute RMQ(i , j ) in D
4. LCA(i, j) = N[RMQ(i , j )]
O(n)
O(1)
O(n)
O(n)
O(1)
O(1)
O(1)
This gives us O(n) space, O(n) prep. time and O(1) query time
for the LCA problem
by using the solution to ±1RMQ

145. Ongoing Summary
We have seen an O(n) space, O(n) prep. time and O(1) query time solution
for the Lowest Common Ancestor problem
which uses the solution to ±1RMQ
We have seen an O(n) space, O(n) prep. time and O(1) query time solution
for the ±1 Range Minimum Query problem
which improves solution 3 for RMQ from last lecture
(but only for ±1 inputs)

146. Ongoing Summary
What about the general Range Minimum Query problem?
We have seen an O(n) space, O(n) prep. time and O(1) query time solution
for the Lowest Common Ancestor problem
which uses the solution to ±1RMQ
We have seen an O(n) space, O(n) prep. time and O(1) query time solution
for the ±1 Range Minimum Query problem
which improves solution 3 for RMQ from last lecture
(but only for ±1 inputs)
(when the inputs aren’t ±1)

147. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
Build the Cartesian tree, TA of the array A:
6 13

148. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
6 13

149. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
6 13

150. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
partitions the array in two
6 13

151. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
17 823 73 51 82 19 32 67 91 14 46 9 21 54
partitions the array in two
6 13

152. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
17 823 73 51 82 19 32 67 91 14 46 9 21 54
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
6 13

153. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
17 823 73 51 82 19 32 67 91 14 46 9 21 54
8 9
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
6 13

154. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location 8 9
1723 73 51 82 19 32 67 91 14 46 21 54
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
6 13

155. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location 8 9
1723 73 51 82 19 32 67 91 14 46 21 54
17 14 21
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
6
19
13

156. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location 8 9
17 14 21
23 73 51 82 32 67 91 46 54
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
6
19
13

157. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location 8 9
17 14 21
23 73 51 82 32 67 91 46 54
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
6
23 51 67 46 5432
19
13

158. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location 8 9
17 14 21
73 82 91
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
6
23 51 67 46 5432
19
13

159. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location 8 9
17 14 21
73 82 91
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
6
23 51 67 46 5432
19
13

160. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
This process isn’t very efficient. . .
a better one takes O(n) time
8 9
17 14 21
73 82 91
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
6
23 51 67 46 5432
19
13

161. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
This process isn’t very efficient. . .
a better one takes O(n) time
8 9
17 14 21
73 82 91
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
it’s not tricky but we don’t have
time to cover it
6
23 51 67 46 5432
19
13

162. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
This process isn’t very efficient. . .
a better one takes O(n) time
8 9
17 14 21
73 82 91
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
it’s not tricky but we don’t have
time to cover it
Key Fact: The LCA in TA equals the RMQ in A
6
23 51 67 46 5432
19
13

163. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46
i = 3 j = 7
RMQ(3, 7) = 6
9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
This process isn’t very efficient. . .
a better one takes O(n) time
8 9
17 14 21
73 82 91
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
it’s not tricky but we don’t have
time to cover it
Key Fact: The LCA in TA equals the RMQ in A
6
23 51 32 67 46 54
73
32
19
13

164. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
This process isn’t very efficient. . .
a better one takes O(n) time
8 9
17 14 21
73 82 91
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
it’s not tricky but we don’t have
time to cover it
Key Fact: The LCA in TA equals the RMQ in A
6
23 51 67 46 5432
19
13

165. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
This process isn’t very efficient. . .
a better one takes O(n) time
8 9
17 14 21
73 82 91
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
it’s not tricky but we don’t have
time to cover it
Key Fact: The LCA in TA equals the RMQ in A
6
23 51 67 46 5432
19
9
91
54
i = 10 j = 15
13

166. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
This process isn’t very efficient. . .
a better one takes O(n) time
8 9
17 14 21
73 82 91
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
it’s not tricky but we don’t have
time to cover it
Key Fact: The LCA in TA equals the RMQ in A
This gives us O(n) space, O(n) prep. time and O(1) query time
for the RMQ problem
6
23 51 67 46 5432
19
9
91
54
i = 10 j = 15
13

167. Solving RMQs using LCAs
A
n
17 823 73 51 82 19 32 5 67 91 14 46 9 21 54
0 1 2 3 4 5 7 8 9 10 11 12 14 15
5
Build the Cartesian tree, TA of the array A:
• The root is the smallest value
• The selected location
This process isn’t very efficient. . .
a better one takes O(n) time
8 9
17 14 21
73 82 91
partitions the array in two
• The rest of the tree is given by
recursing left and right. . .
it’s not tricky but we don’t have
time to cover it
Key Fact: The LCA in TA equals the RMQ in A
This gives us O(n) space, O(n) prep. time and O(1) query time
for the RMQ problem
6
23 51 67 46 5432
19
9
91
54
i = 10 j = 15
13
by using the solution to LCA :)

168. Summary
We have seen an O(n) space, O(n) prep. time and O(1) query time solution
for the Range Minimum Query problem
which uses the solution to LCA
We have seen an O(n) space, O(n) prep. time and O(1) query time solution
for the Lowest Common Ancestor problem
which uses the solution to ±1RMQ
We have seen an O(n) space, O(n) prep. time and O(1) query time solution
for the ±1 Range Minimum Query problem
which improves solution 3 for RMQ from last lecture
(but only for ±1 inputs)
(which works for all inputs)