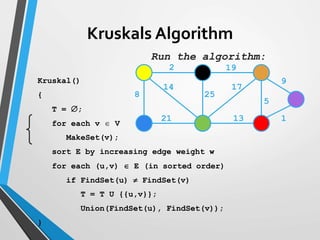
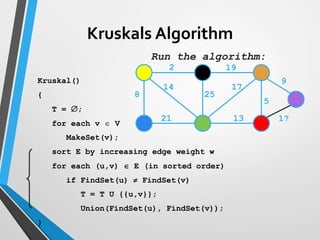
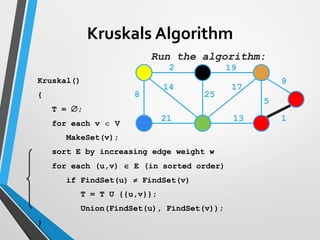
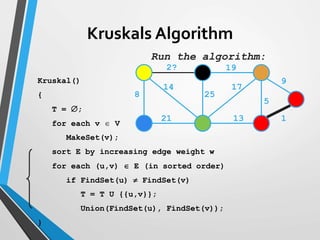
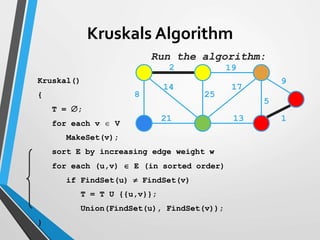
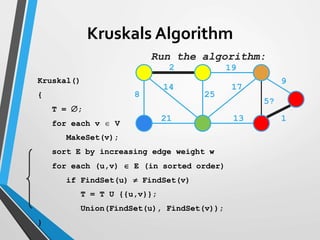
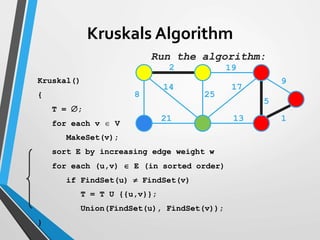
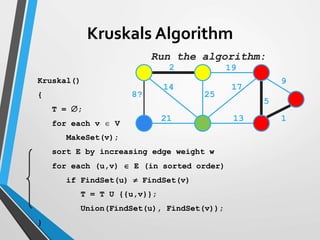
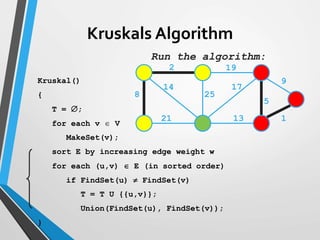
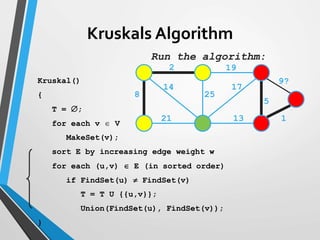
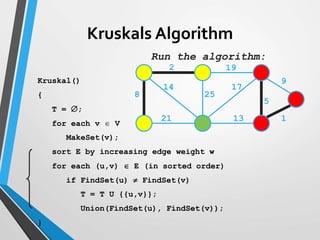
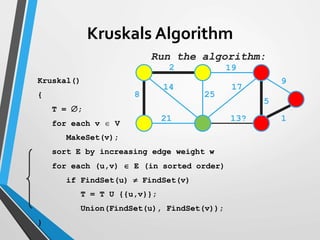
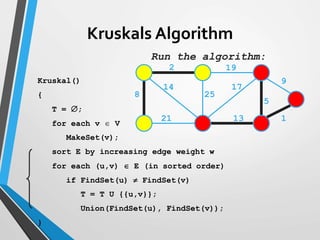
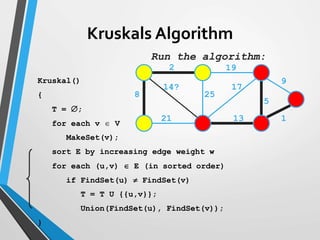
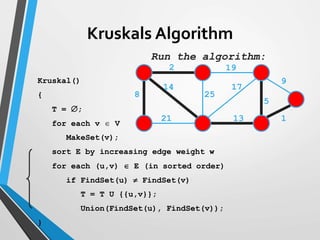
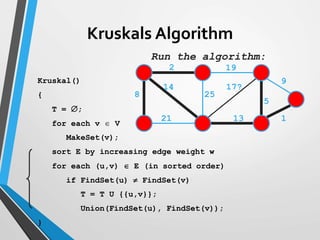
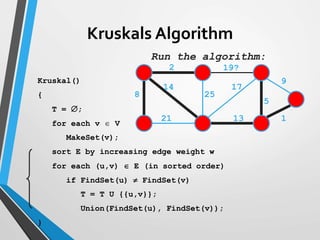
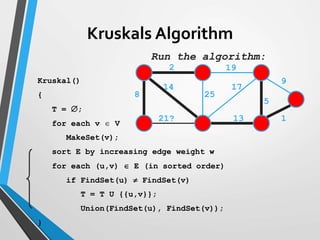
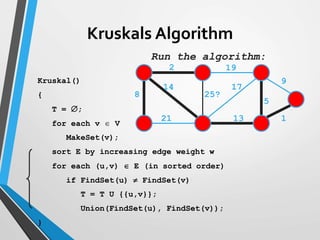
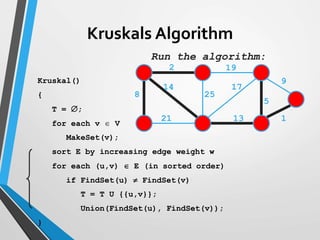
The document discusses minimum spanning trees (MST) and two algorithms for finding them: Prim's algorithm and Kruskal's algorithm. Prim's algorithm operates by building the MST one vertex at a time, starting from an arbitrary root vertex and at each step adding the cheapest connection to another vertex not yet included. Kruskal's algorithm finds the MST by sorting the edges by weight and sequentially adding edges that connect different components without creating cycles.

1. Saga Valsalan
www.SagaValsalan.blogspot.in
www.YouTube.com/SagaValsalan
www.Facebook.com/SagaValsalan

2. Minimum SpanningTrees (MST)
• A minimum spanning tree (MST) or minimum weight
spanning tree is a spanning tree of a connected, undirected
graph.
• It connects all the vertices together with the minimal total
weighting for its edges.
• MST is a tree ,because it is acyclic
• Any undirected graph has a minimum spanning forest, which
is a union of minimum spanning trees for its connected
components.
• If a graph has N vertices then the spanning tree will have N-1
edges
Minimum SpanningTrees (MST)

3. Minimum SpanningTrees (MST)
2 19
9
1
5
13
17
25
14
8
21

4. Prims Algorithm
• Prim's algorithm is a greedy algorithm that finds a
minimum spanning tree for a weighted undirected graph.
• It finds a subset of the edges that forms a tree that
includes every vertex, where the total weight of all the
edges in the tree is minimized.
• The algorithm operates by building this tree one vertex at
a time, from an arbitrary starting vertex, at each step
adding the cheapest possible connection from the tree to
another vertex.

5. Prims Algorithm
Procedure:
• Initialize the min priority queue Q to contain all the
vertices.
• Set the key of each vertex to ∞ and root’s key is set to
zero
• Set the parent of root to NIL
• If weight of vertex is less than key value of the vertex,
connect the graph.
• Repeat the process till all vertex are used.

6. MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Initialize the min priority queue Q to contain
all the vertices.
Set the key of each vertex to ∞
Set the parent of root to NIL
Root’s key is set to 0
Until queue become null set
Input– Graph, Weight, Root
Set the parent of ‘v’ as ‘u’
Set the key of v = weight of edge
connecting uv
Prims Algorithm

7. MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
14
10
3
6 4
5
2
9
15
8
Run on example graph
Prims Algorithm

8.   
  


14
10
3
6 4
5
2
9
15
8
Run on example graph
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

9.   
0  


14
10
3
6 4
5
2
9
15
8
Pick a start vertex r
r
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

10.   
0  


14
10
3
6 4
5
2
9
15
8
Black vertices have been removed from Q
u
Prims Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);

11.   
0  
3

14
10
3
6 4
5
2
9
15
8
Black arrows indicate parent pointers
u
Prims Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);

12. 14  
0  
3

14
10
3
6 4
5
2
9
15
8
u
Prims Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);

13. 14  
0  
3

14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

14. 14  
0 8 
3

14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

15. 10  
0 8 
3

14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

16. 10  
0 8 
3

14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

17. 10 2 
0 8 
3

14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

18. 10 2 
0 8 15
3

14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

19. 10 2 
0 8 15
3

14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

20. 10 2 9
0 8 15
3

14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

21. 10 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

22. 5 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

23. 5 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

24. 5 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

25. 5 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

26. 5 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
Prims Algorithm

27. MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
5 2 9
0 8 15
3
4
3
4
5
2
9
15
8
Prims Algorithm

28. Kruskals Algorithm
• Kruskal's algorithm is a minimum-spanning-tree
algorithm which finds an edge of the least possible
weight that connects any two trees in the forest.
• It is a greedy algorithm, adding increasing cost arcs
at each step.
• This means it finds a subset of the edges that forms
a tree that includes every vertex, where the total
weight of all the edges in the tree is minimized.
• To visit all nodes, with minimum cost, without cycle
formation

29. Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm
T-Tree
E-Edge
V-Vertices
v-Vertex
MakeSet(x): S = S U {{x}}
Union(Si, Sj): S = S - {Si, Sj} U {Si U Sj}
FindSet(X): return Si  S such that x  Si

30. 2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

31. 2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

32. 2 19
9
1?
5
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

33. 2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

34. 2? 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

35. 2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

36. 2 19
9
1
5?
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

37. 2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

38. 2 19
9
1
5
13
17
25
14
8?
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

39. 2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

40. 2 19
9?
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

41. 2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

42. 2 19
9
1
5
13?
17
25
14
8
21
Run the algorithm:
Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
Kruskals Algorithm

43. Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskals Algorithm

44. Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
2 19
9
1
5
13
17
25
14?
8
21
Run the algorithm:
Kruskals Algorithm

45. Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskals Algorithm

46. Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
2 19
9
1
5
13
17?
25
14
8
21
Run the algorithm:
Kruskals Algorithm

47. Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
2 19?
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskals Algorithm

48. Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
2 19
9
1
5
13
17
25
14
8
21?
Run the algorithm:
Kruskals Algorithm

49. Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
2 19
9
1
5
13
17
25?
14
8
21
Run the algorithm:
Kruskals Algorithm

50. Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskals Algorithm

51. Kruskal()
{
T = ;
for each v  V
MakeSet(v);
sort E by increasing edge weight w
for each (u,v)  E (in sorted order)
if FindSet(u)  FindSet(v)
T = T U {{u,v}};
Union(FindSet(u), FindSet(v));
}
2 19
9
1
5
13
17
25
14
8
21
Run the algorithm:
Kruskals Algorithm

52. ThankYou