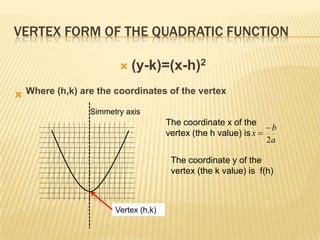
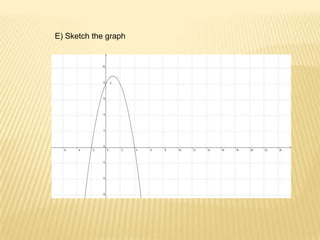
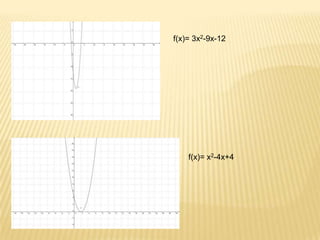
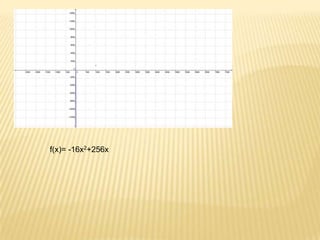
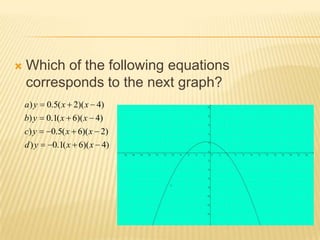
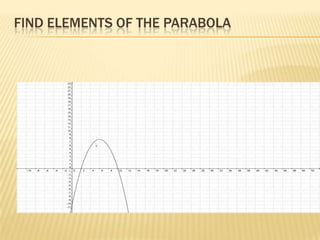
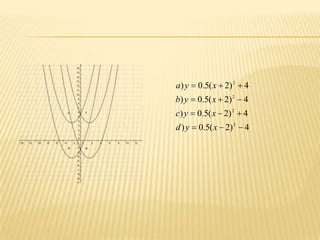
The document discusses quadratic functions and their key properties. It defines a quadratic function as a polynomial function of second degree whose graph is a parabola. The standard form of a quadratic function is given as f(x) = ax^2 + bx + c, where a, b, and c are constants and a cannot equal 0. It also discusses the vertex form of a quadratic function and how to find the vertex, x-intercepts, y-intercept, equation of the symmetry axis, and sketch the graph of example quadratic functions.

1. QUADRATIC FUNCTION

2. QUADRATIC FUNCTION
 It´s a polynomial function of second degree,
whose graph is a curve called parabola.
f ( x) a x2 bx c
 Where a,b and c are constan, c is the interts,
a≠0 , c is the y-intercept.

3. VERTEX FORM OF THE QUADRATIC FUNCTION
 (y-k)=(x-h)2
 Where (h,k) are the coordinates of the vertex
Simmetry axis
The coordinate x of the
b
vertex (the h value) is x
2a
The coordinate y of the
vertex (the k value) is f(h)
Vertex (h,k)

4.  The vertex can be a maximum value or a
minimum value.
 The vertex is maximum if the parabola opens
downwards a<0
The vertex is minimum if the parabola opens
upwards a>0

5. Solve: f(x)= -x2+2x+8 a=-1 b=2
c=8
A) Find the roots(x intercepts)
B) Find the vertex
C) Find the y-intercept
D) Write the equation of the symmetry axis
E) Sketch the graph
C) Find the y-intercept c=8
A) 0=-x2+2x+8
0=-(x2-2x-8) D) Write the equation of the symmetry axis
0=(x2-2x-8) x=1
0=(x-4)(x+2)
Roots are x=4, x=-2
B) Find the vertex(h,k)
h= -b/2 a = -(2)/2(-1) = 1
k= f(h)= -(1)2+2(1)+8 = 9

6. E) Sketch the graph

7. SOLVE F(X)= 3X2-9X-12
 A) Find the roots(x intercepts)
 B) Find the vertex
 C) Find the y-intercept
 D) Write the equation of the symmetry axis
 E) Sketch the graph
 f(x)= 3x2-9x-12
 f(x)= x2-4x+4
 f(x)= -16x2+256x

8. f(x)= 3x2-9x-12
f(x)= x2-4x+4

9. f(x)= -16x2+256x

10.  Which of the following equations
corresponds to the next graph?
a) y 0.5( x 2)( x 4)
b) y 0.1( x 6)( x 4)
c) y 0.5( x 6)( x 2)
d)y 0.1( x 6)( x 4)

11.  Match each equation with the corresponding
graph
2
a) y 0.5 x
2
b) y 0.5 x
2
c) y 0.2 x
d)y 2.5 x 2

12. FIND ELEMENTS OF THE PARABOLA

13. a) y 0.5( x 2) 2 4
b) y 0.5( x 2) 2 4
c) y 0.5( x 2) 2 4
d)y 0.5( x 2) 2 4