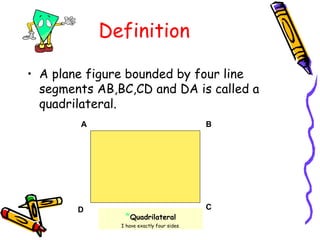
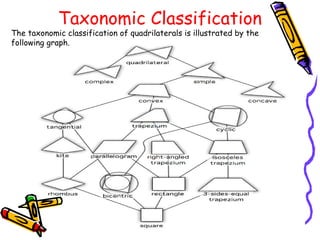
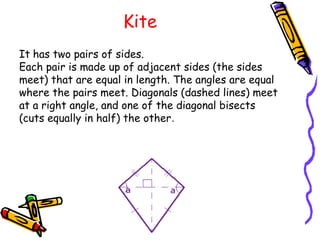
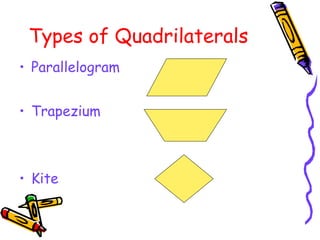
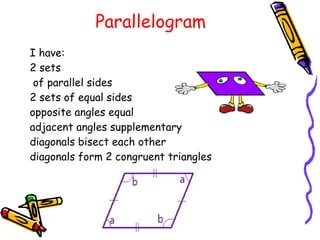
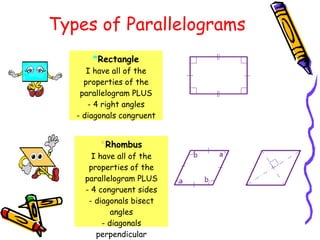
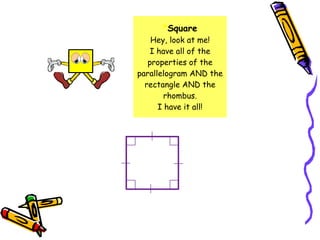
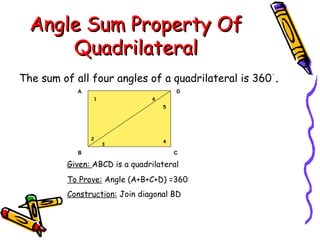
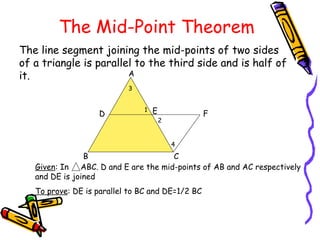
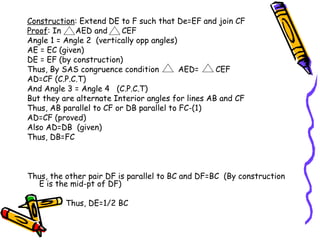
1) A quadrilateral is a polygon with four sides and four vertices. There are over 9 million types of quadrilaterals that can be classified as simple or complex. 2) Quadrilaterals include parallelograms, trapezoids, kites, and more. A parallelogram has two sets of parallel sides and opposite/adjacent angles are equal. A square is a special type of rectangle and parallelogram. 3) The interior angles of any quadrilateral sum to 360 degrees. The line segment between the midpoints of two sides of a triangle is parallel to the third side and half its length.

1. MATHS PROJECT
Quadrilaterals
- Shaunak Bhima ni
IX-B

2. Definition
• A plane figure bounded by four line
segments AB,BC,CD and DA is called a
quadrilateral.
A B
D C
*Quadrilateral
I have exactly four sides.

3. In geometry, a quadrilateral is a polygon with four
sides and four vertices. Sometimes, the term
quadrangle is used, for etymological symmetry with
triangle, and sometimes tetragon for consistence with
pentagon.
There are over 9,000,000 quadrilaterals. Quadrilaterals
are either simple (not self-intersecting) or complex
(self-intersecting). Simple quadrilaterals are either
convex or concave.

4. Taxonomic Classification
The taxonomic classification of quadrilaterals is illustrated by the
following graph.

5. Types of Quadrilaterals
• Parallelogram
• Trapezium
• Kite

7. Parallelogram
I have:
2 sets
of parallel sides
2 sets of equal sides
opposite angles equal
adjacent angles supplementary
diagonals bisect each other
diagonals form 2 congruent triangles

8. Types of Parallelograms
*Rectangle
I have all of the
properties of the
parallelogram PLUS
- 4 right angles
- diagonals congruent
*Rhombus
I have all of the
properties of the
parallelogram PLUS
- 4 congruent sides
- diagonals bisect
angles
- diagonals
perpendicular

9. *Square
Hey, look at me!
I have all of the
properties of the
parallelogram AND the
rectangle AND the
rhombus.
I have it all!

10. Is a square a rectangle?
Some people define categories exclusively, so that a rectangle is a
quadrilateral with four right angles that is not a square. This is
appropriate for everyday use of the words, as people typically use
the less specific word only when the more specific word will not do.
Generally a rectangle which isn't a square is an oblong.
But in mathematics, it is important to define categories inclusively,
so that a square is a rectangle. Inclusive categories make
statements of theorems shorter, by eliminating the need for tedious
listing of cases. For example, the visual proof that vector addition is
commutative is known as the "parallelogram diagram". If categories
were exclusive it would have to be known as the "parallelogram (or
rectangle or rhombus or square) diagram"!

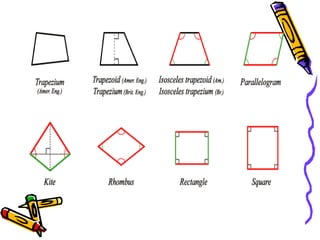
11. Trapezium
I have only one set of parallel sides.
[The median of a trapezium is parallel to the
bases and equal to one-half the sum of the
bases.]
Trapezoid Regular Trapezoid

12. Kite
It has two pairs of sides.
Each pair is made up of adjacent sides (the sides
meet) that are equal in length. The angles are equal
where the pairs meet. Diagonals (dashed lines) meet
at a right angle, and one of the diagonal bisects
(cuts equally in half) the other.

13. Some other types of
quadrilaterals
Cyclic quadrilateral: the four
vertices lie on a circumscribed circle.
Tangential quadrilateral: the four
edges are tangential to an inscribed
circle. Another term for a tangential
polygon is inscriptible.
Bicentric quadrilateral: both cyclic
and tangential.

14. Angle Sum Property Of
Quadrilateral
.
The sum of all four angles of a quadrilateral is 360 .
A D
1 6
5
2
4
3
B C
Given: ABCD is a quadrilateral
To Prove: Angle (A+B+C+D) =360.
Construction: Join diagonal BD

15. Proof: In ABD
Angle (1+2+6)=180 - (1)
(angle sum property of )
In BCD
Similarly angle (3+4+5)=180 – (2)
Adding (1) and (2)
Angle(1+2+6+3+4+5)=180+180=360
Thus, Angle (A+B+C+D)= 360

16. The Mid-Point Theorem
The line segment joining the mid-points of two sides
of a triangle is parallel to the third side and is half of
it. A
3
D
1 E F
2
4
B C
Given: In ABC. D and E are the mid-points of AB and AC respectively
and DE is joined
To prove: DE is parallel to BC and DE=1/2 BC

17. Construction: Extend DE to F such that De=EF and join CF
Proof: In AED and CEF
Angle 1 = Angle 2 (vertically opp angles)
AE = EC (given)
DE = EF (by construction)
Thus, By SAS congruence condition AED= CEF
AD=CF (C.P.C.T)
And Angle 3 = Angle 4 (C.P.C.T)
But they are alternate Interior angles for lines AB and CF
Thus, AB parallel to CF or DB parallel to FC-(1)
AD=CF (proved)
Also AD=DB (given)
Thus, DB=FC
Thus, the other pair DF is parallel to BC and DF=BC (By construction
E is the mid-pt of DF)
Thus, DE=1/2 BC

18. THE END
- Shaunak Bhimani
IX-B
ROLL NO. 04