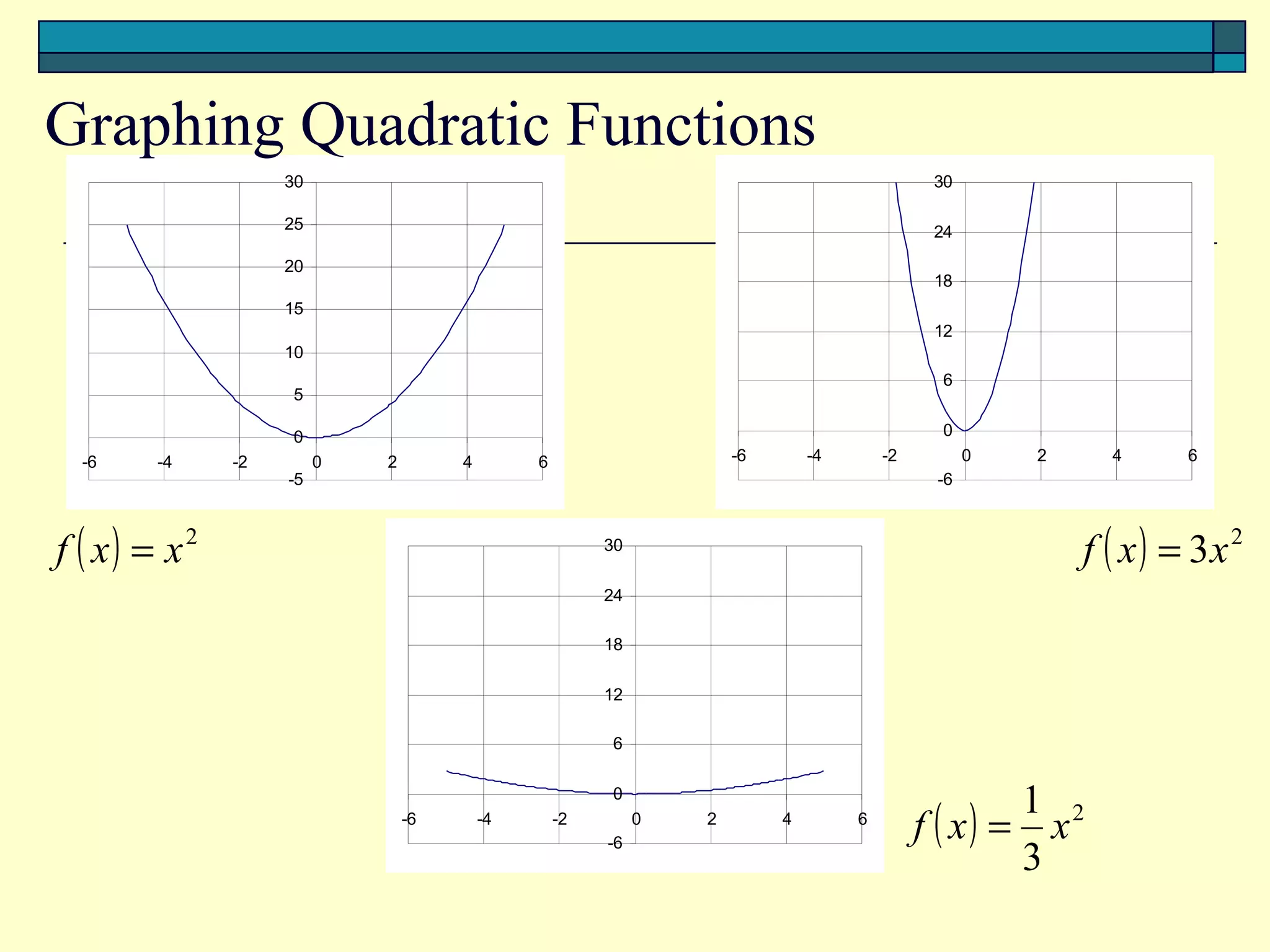
The document discusses graphing quadratic functions of the form f(x) = ax^2 + bx + c. The key points are: 1) The graph of any quadratic function is a parabola. 2) To graph f(x) = a(x - h)^2 + k, find the vertex (h, k), x-intercepts by setting f(x) = 0, y-intercept, and plot points to form the parabola shape. 3) The vertex of f(x) = ax^2 + bx + c is (-b/2a, f(-b/2a)), which is the minimum if a > 0 and maximum if a

1. Graphing Quadratic Functions
Graphs of Quadratic Functions
Any quadratic function can be expressed in the form
f ( x ) = ax 2 + bx + c, a ≠ 0
Where a, b, c are real numbers and the graph of any quadratic function is called
a parabola.

2. Graphing Quadratic Functions
30 30
25 24
20
18
15
12
10
6
5
0 0
-6 -4 -2 0 2 4 6 -6 -4 -2 0 2 4 6
-5 -6
f ( x) = x2 30
f ( x ) = 3x 2
24
18
12
6
1 2
f ( x) =
0
-6 -4 -2
-6
0 2 4 6
x
3

3. Graphing Quadratic Functions
Graphing Quadratic Functions With Equations in
the Form f ( x ) = a( x − h ) 2T k
+
To graph f ( x ) = a( x − h ) 2 + k ,
1) Determine whether the parabola opens upward or downward. If a > 0, it
opens upward. It a < 0, it opens downward.
2) Determine the vertex of the parabola. The vertex is (h, k).
3) Find any x-intercepts by replacing f (x) with 0. Solve the resulting Quadratic
equation for x.
4) Find the y-intercept by replacing x with 0.
5) Plot the intercepts and vertex and additional points as necessary. Connect
these points with a smooth curve that is shaped like a cup.

4. Graphing Quadratic Functions
EXAMPLE
Graph the function f ( x ) = −2( x + 4 ) − 8.
2
SOLUTION
1) Determine how the parabola opens.
2) Find the vertex. The vertex of the parabola is at (h, k).
3) Find the x-intercepts.
4) Find the y-intercept.
5) Graph the parabola.

5. Graphing Quadratic Functions
The Vertex of a Parabola Whose Equation is
f ( x ) = ax 2 +T + c
bx
Consider the parabola defined by the quadratic function
f ( x ) = ax 2 + bx + c.
The parabola’s vertex is
 b  b 
− ,
 2a f  −  .
  2a  


6. Graphing Quadratic Functions
EXAMPLE
Graph the function f ( x) = 6 − 4x + x2.
SOLUTION
1) Determine how the parabola opens.
2) Find the vertex.
3) Find the x-intercepts.
4) Find the y-intercept.
5) Graph the parabola.

7. Minimums & Maximums
Minimum and Maximum: Quadratic Functions
Consider f ( x ) = ax 2 + bx + c.
1) If a > 0, then f has a minimum that occurs at x = − b .
2a
This minimum value is f  − b .
 
 2a 
b
2) If a < 0, then f has a maximum that occurs at x = − .
2a
This maximum value is f  − b .
 
 2a 

8. Minimums & Maximums
EXAMPLE
A person standing close to the edge on the top of a 200-foot
building throws a baseball vertically upward. The quadratic
function
s ( t ) = −16t 2 + 64t + 200
models the ball’s height above the ground, s (t), in feet, t
seconds after it was thrown.
When will the ball reach its highest point? How high is it?
How many seconds does it take until the ball finally hits the
ground? Round to the nearest tenth of a second.

9. 11.3 Quadratic Functions & Their Graphs
Reference: Blitzer’s Introductory and Intermediate Algebra