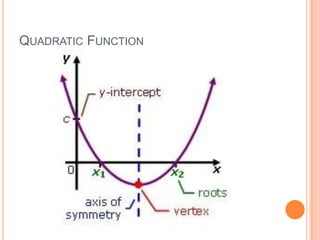
The document provides an overview of quadratic functions and their transformations. It defines key concepts like parabolas, quadratic functions, vertex form, and the parent function. It explains how to graph quadratic functions and how their graphs are transformed through reflection, stretching, compression, and translation based on changes to the coefficients in the function. Examples are provided to demonstrate finding features of quadratic functions like the vertex, axis of symmetry, minimum/maximum values, and describing the transformations.

1. 4-1 QUADRATIC FUNCTIONS AND
TRANSFORMATIONS
Chapter 4 Quadratic Functions and Equations
©Tentinger

2. ESSENTIAL UNDERSTANDING AND
OBJECTIVES
 Essential Understanding: The graph of any
quadratic function is the transformation of the graph
of the parent function y = x2
 Objectives:
 Students will be able to:
 Identify and graph quadratic functions
 Identify and graph the transformations of quadratic
functions (reflect, stretch, compression, translation)
 Solve for the minimum and maximum values of
parabolas

3. IOWA CORE CURRICULUM
 Algebra
 A.CED.1. Create equations and inequalities in one variable and use
them to solve problems. Include equations arising from linear and
quadratic functions, and simple rational and exponential functions.
 Functions
 F.IF.4. For a function that models a relationship between two quantities,
interpret key features of graphs and tables in terms of the quantities, and
sketch graphs showing key features given a verbal description of the
relationship.
 F.IF.6. Calculate and interpret the average rate of change of a function
(presented symbolically or as a table) over a specified interval. Estimate
the rate of change from a graph.
 F.IF.7. Graph functions expressed symbolically, and show features of the
graph, by hand in simple cases and using technology for more
complicated cases.
 F.BF.3. Identify the effect on the graph of f(x) + k, kf(x), f(kx), and f(x+k)
for specific values of k (both positive and negative); find the value of k
given the graphs. Experiment with cases and illustrate an explanation of
the effects on the graph using technology.

4. VOCABULARY
 Parabola: the graph of a quadratic function, it
makes a U shape
 Quadratic Function: ax2 + bx + c
 Vertex Form: f(x) = a(x – h)2 +k, where a doesn’t
equal zero, vertex is (h, k)
 Axis of Symmetry: line that divides the parabola
into two mirror images. Equation x = h
 Parent Function: y = x2

5. QUADRATIC FUNCTION

6. GRAPHING A QUADRATIC FUNCTION
 Graphing a Function in the form f(x) = ax2
 f(x) = (1/2)x2
 Plot the vertex
 Find and plot two points on one side of the axis of
symmetry
 Plot the corresponding points on other side of the axis of
symmetry
 Sketch the curve
 Graph: f(x) = -(1/3)x2
 What can you say about the graph of the function
f(x) = ax2 if a is a negative number?

7. TRANSFORMATIONS
 Vertex form: f(x) = a(x-h)2 + k
 Reflection: if a is positive the graph opens up, if a is
negative it reflects across the x-axis and opens
downward
 If the parabola opens upward, the y coordinate of the
vertex is a minimum
 If the parabola opens downward, the y coordinate of
the vertex is a maximum
 Stretch a > 1 the graph becomes more narrow
 Compression 0< a < 1 the graph becomes more flat

8. TRANSFORMATIONS
 Standard form: f(x) = a(x-h)2 + k
 Vertical Translation: k value, on the outside of the
parentheses. Moves graph up and down
 Horizontal translation: opposite of the h value, on
the inside of the parentheses. Moves graph left and
right.

9. EXAMPLES
 For the equations below, write the vertex, the axis
of symmetry, the max or min value, and the domain
and range. Then describe the transformations.
 f(x) = x2 – 5
 f(x) = (x – 4)2
 f(x) = -(x + 1)2
 f(x) = 3(x – 4)2 – 2
 f(x) = -2(x +1)2

10. HOMEWORK
 Pg. 199 – 200
 # 9-33 (3s) 35-37, 38, 40 – 42