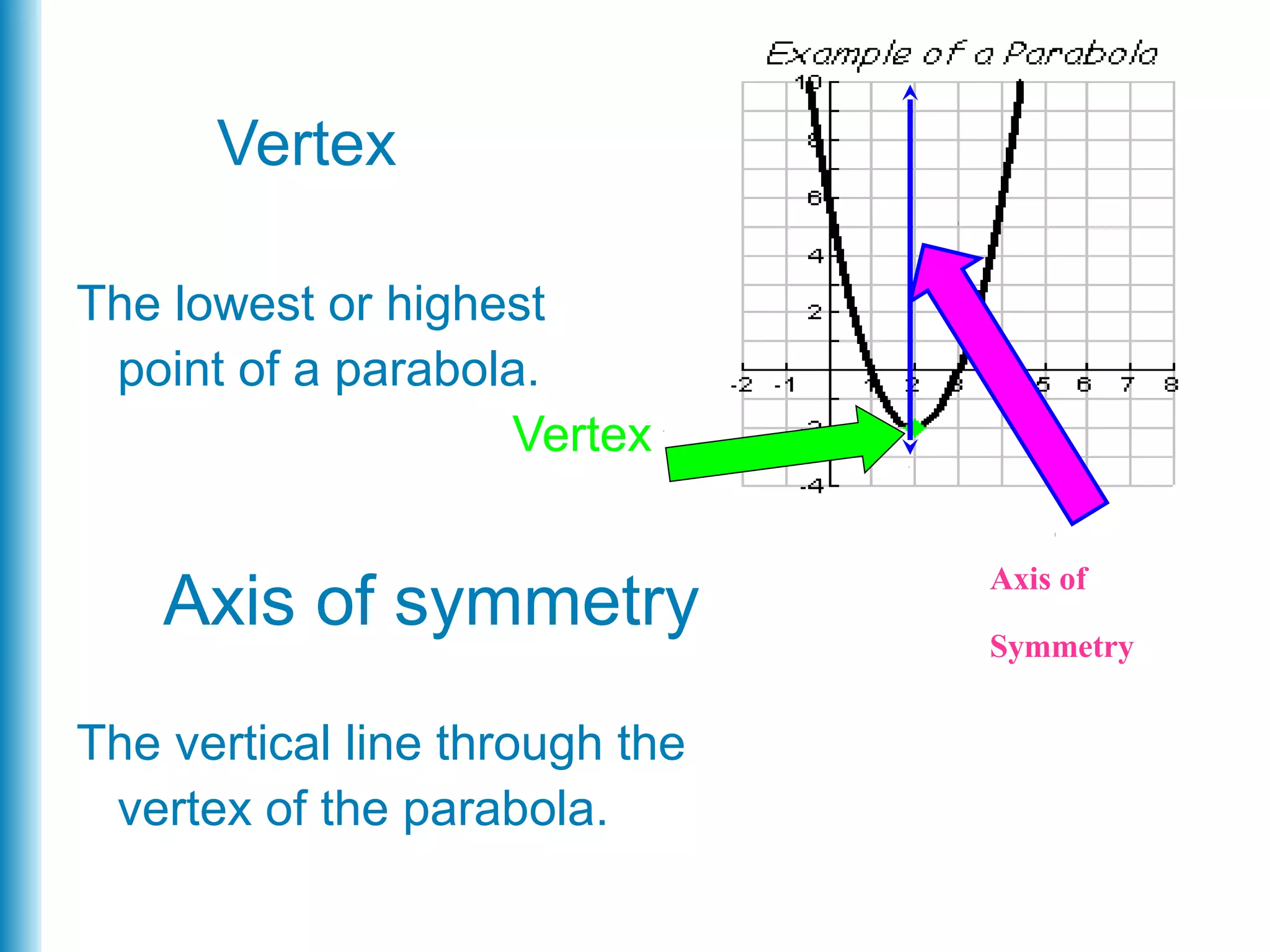
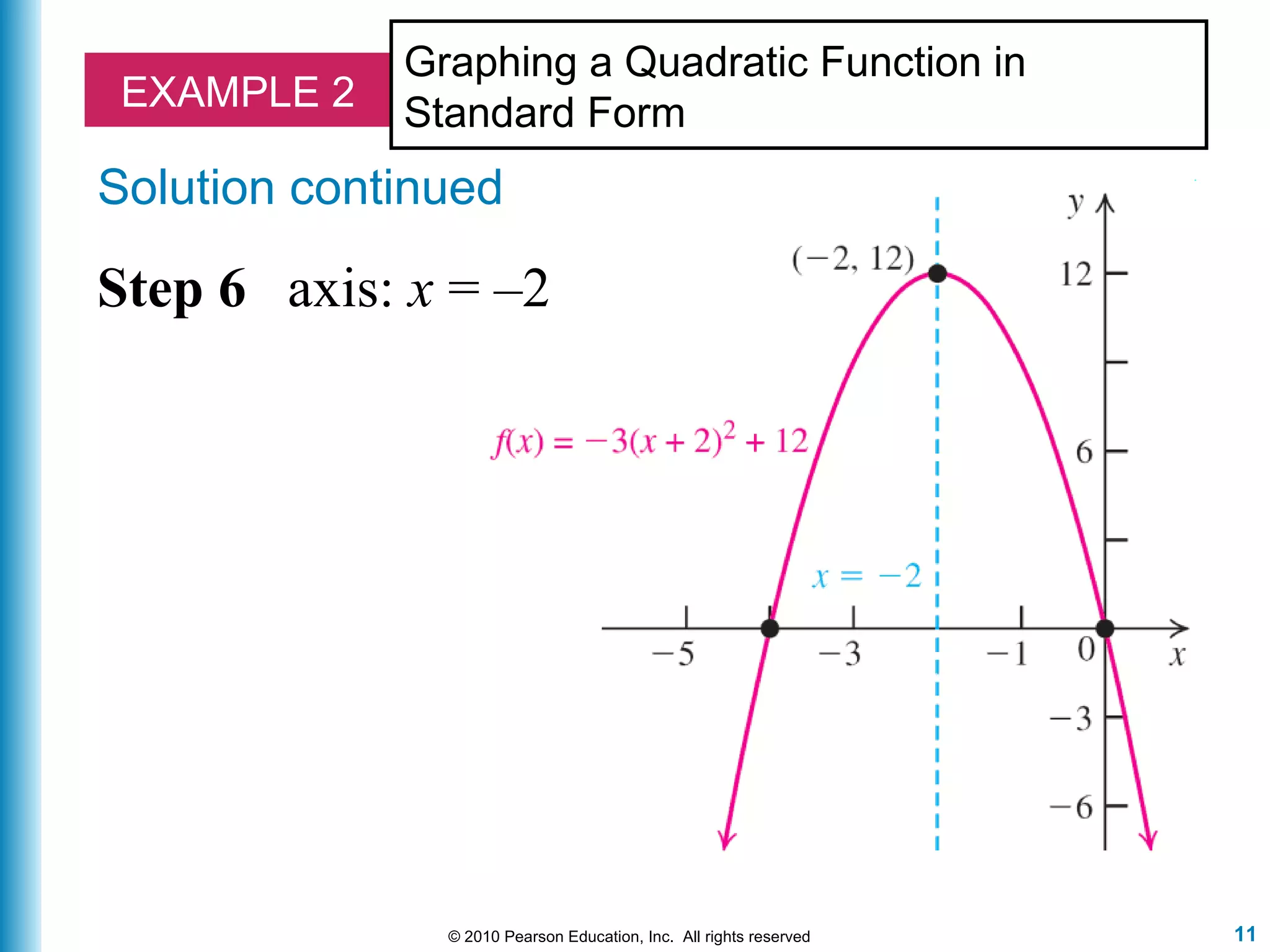
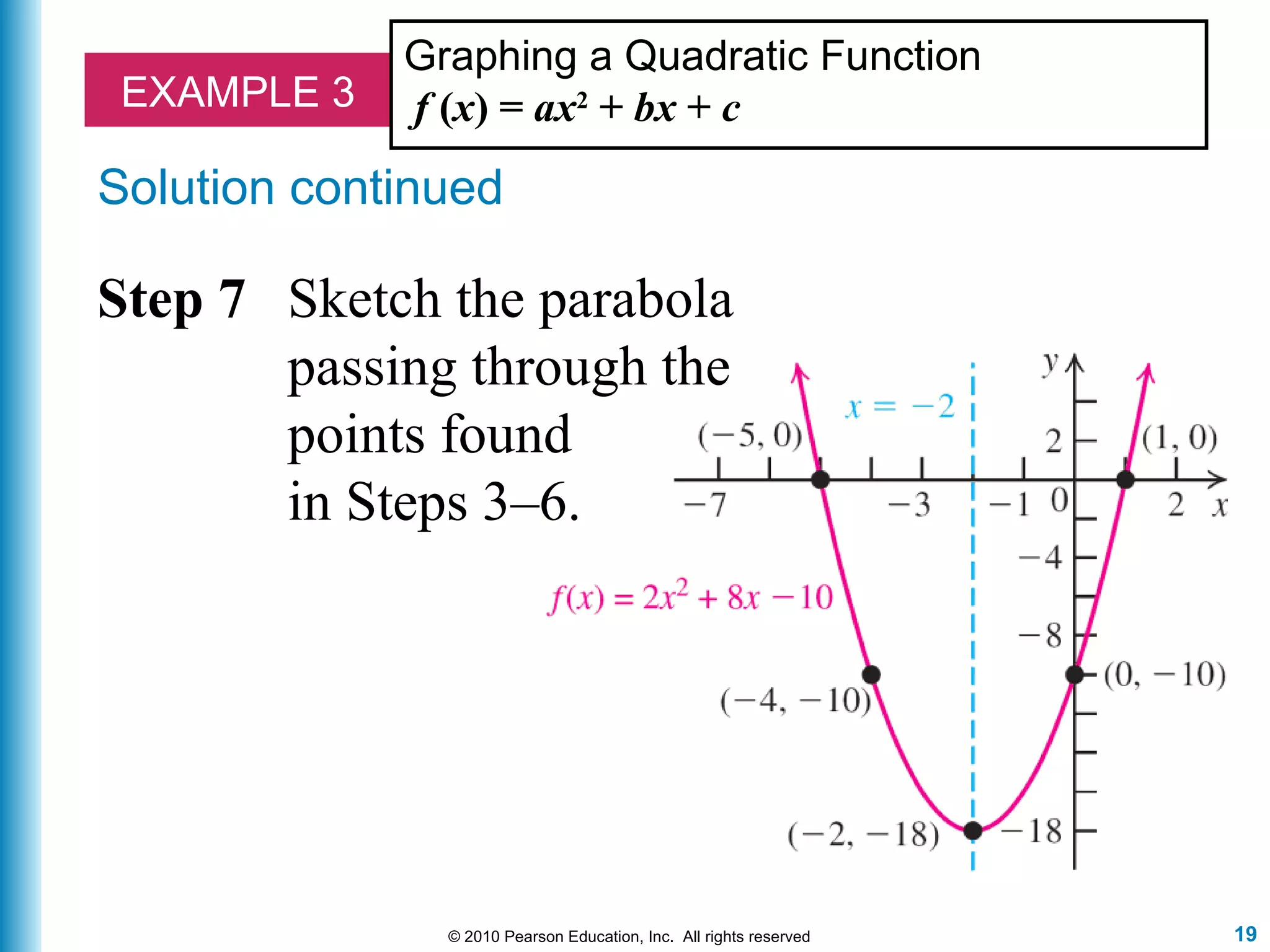
The document discusses quadratic functions and how to graph them. It defines a quadratic function as a function of the form f(x) = ax^2 + bx + c, where a ≠ 0. It explains that the graph of such a function is a parabola, and provides steps to find characteristics of the parabola like the vertex, axis of symmetry, x-intercepts, and y-intercept in order to graph the function. Examples are included to demonstrate applying these steps to graph specific quadratic functions.

1. 1© 2010 Pearson Education, Inc. All rights reserved
QUADRATIC FUNCTION
A function of the form
where a, b, and c, are real numbers with a ≠ 0,
is called a quadratic function.
f x( ) = ax2
+ bx + c,

2. 2© 2010 Pearson Education, Inc. All rights reserved
THE STANDARD FORM OF
A QUADRATIC FUNCTION
The quadratic function
is in standard form. The graph of f is a
parabola with vertex (h, k). The parabola is
symmetric with respect to the line x = h, called
the axis of symmetry of the parabola. If a > 0,
the parabola opens up and k is the minimum
value of f, and if a < 0, the parabola opens down
and k is the maximum value of f.
f x( ) = a x − h( )2
+ k, a ≠ 0

3. Vertex
The lowest or highest
point of a parabola.
Vertex
Axis of symmetry
The vertical line through the
vertex of the parabola.
Axis of
Symmetry

4. 4© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 1 Finding a Quadratic Function
Find the standard form of the quadratic
function whose graph has vertex (–3, 4) and
passes through the point (–4, 7).

5. 5© 2010 Pearson Education, Inc. All rights reserved
PROCEDURE FOR GRAPHING
f (x) = a(x – h)2
+ k
Step 1 The graph is a parabola. Identify a,
h, and k.
Step 2 Determine how the parabola opens.
If a > 0, the parabola opens up.
If a < 0, the parabola opens down.
Step 3 Find the vertex. The vertex is (h, k).
If a > 0 (or a < 0), the function f has
a minimum (or a maximum) value k
at x = h.

6. 6© 2010 Pearson Education, Inc. All rights reserved
PROCEDURE FOR GRAPHING
f (x) = a(x – h)2
+ k
Step 4 Find the x-intercepts (if any). Set
f (x) = 0 and solving the
equation a(x – h)2
+ k = 0 for
x.
If the solutions are real numbers, they
are the x-intercepts. If not, the
parabola either lies above the x-axis
(when a > 0) or below the x-axis
(when a < 0).

7. 7© 2010 Pearson Education, Inc. All rights reserved
PROCEDURE FOR GRAPHING
f (x) = a(x – h)2
+ k
Step 6 Sketch the graph. Plot the points
found in Steps 3–5 and join them by a
parabola. Show the axis x = h of the
parabola by drawing a dashed line.
Step 5 Find the y-intercept. Replace x with
0. Then f (0) = ah2
+ k is the
y-intercept.

8. 8© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 2
Graphing a Quadratic Function in
Standard Form
Sketch the graph of ( ) ( )
2
3 2 12.f x x= − + +
Solution
Step 1 a = –3, h = –2, and k = 12
Step 2 a = –3, a < 0, the parabola opens down.
Step 3 (h, k) = (–2, 12); the function f has a
maximum value 12 at x = –2.

9. 9© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 2
Graphing a Quadratic Function in
Standard Form
Step 4 Set f (x) = 0 and solve for x.
( )
( )
( )
2
2
2
0 3 2 12
12 3 2
4 2
x
x
x
= − + +
− = − +
= +
2 2
0 or 4
-intercepts: 0 and 4
x
x x
x
+ = ±
= = −
−
Solution continued

10. 10© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 2
Graphing a Quadratic Function in
Standard Form
Solution continued
Step 5 Replace x with 0.
( ) ( )
( )
2
0 3 0 2 12
3 4 12 0
-intercept is 0 .
f
y
= − + +
= − + =

11. 11© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 2
Graphing a Quadratic Function in
Standard Form
Solution continued
Step 6 axis: x = –2

12. 12© 2010 Pearson Education, Inc. All rights reserved
PROCEDURE FOR GRAPHING
f (x) = ax2
+ bx + c
Step 1 The graph is a parabola. Identify a,
b, and c.
Step 2 Determine how the parabola opens.
If a > 0, the parabola opens up.
If a < 0, the parabola opens down.
Step 3 Find the vertex (h, k). Use the
formula:
( ), , .
2 2
b b
h k f
a a
  
= − − ÷ ÷
  

13. 13© 2010 Pearson Education, Inc. All rights reserved
Step 4 Find the x-intercepts (if any).
Let y = f (x) = 0. Find x by solving
the equation ax2
+ bx + c = 0. If the
solutions are real numbers, they are the
x-intercepts. If not, the parabola either
lies above the x-axis (when a > 0) or
below the x-axis (when a < 0).
PROCEDURE FOR GRAPHING
f (x) = ax2
+ bx + c

14. 14© 2010 Pearson Education, Inc. All rights reserved
Step 5 Find the y-intercept. Let x = 0. The
result f (0) = c is the y-intercept.
Step 7 Draw a parabola through the points
found in Steps 3–6.
Step 6 The parabola is symmetric with
respect to its axis,
Use this symmetry to find additional
points.
.
2
b
x
a
= −
PROCEDURE FOR GRAPHING
f (x) = ax2
+ bx + c

15. 15© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 3
Graphing a Quadratic Function
f (x) = ax2
+ bx + c
Solution
Sketch the graph of ( ) 2
2 8 10.f x x x= + −
Step 1 a = 2, b = 8, and c = –10
Step 2 a = 2, a > 0, the parabola opens up.

16. 16© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 3
Graphing a Quadratic Function
f (x) = ax2
+ bx + c
Step 3 Find (h, k).
( )
( ) ( ) ( )
( ) ( )
2
2
2 2
2 2 2 8 2 10 18
, 2, 18
8
2
b
h
a
k f
h k
= − = − = −
= − = − + − − = −
= − −
Minimum value of –18 at x = –2
Solution continued

17. 17© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 3
Graphing a Quadratic Function
f (x) = ax2
+ bx + c
Solution continued
Step 4 Let f (x) = 0.
2
2 8 10 0x x+ − =
x-intercepts: –5 and 1

18. 18© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 3
Graphing a Quadratic Function
f (x) = ax2
+ bx + c
Solution continued
( ) ( ) ( )
2
0 2 0 8 0 10
-intercept is 10 .
f
y
= + −
−
Step 5 Let x = 0.
Step 6 Axis of symmetry is x = –2. The
symmetric image of (0, –10) with
respect to the axis x = –2 is (–4, –10).

19. 19© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 3
Graphing a Quadratic Function
f (x) = ax2
+ bx + c
Solution continued
Step 7 Sketch the parabola
passing through the
points found
in Steps 3–6.

20. 20© 2010 Pearson Education, Inc. All rights reserved
EXAMPLE 4
Identifying the Characteristics of a
Quadratic Function from Its Graph
The graph of f (x) = –2x2
+8x – 5 is shown.
Find the domain and range of f.
Solution
The domain is (–∞, ∞).
The range is (–∞, 3].