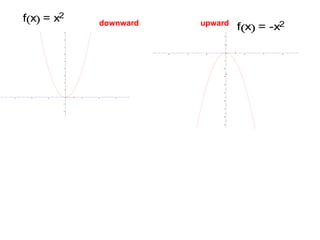
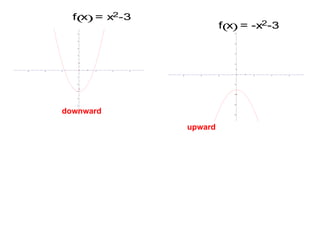
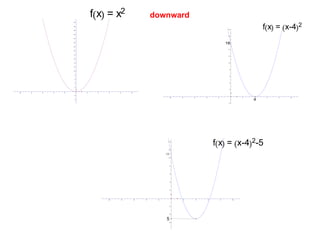
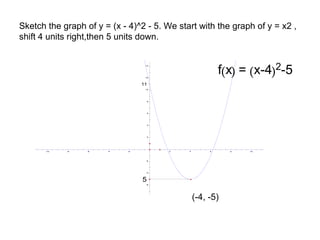
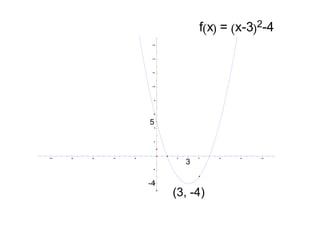
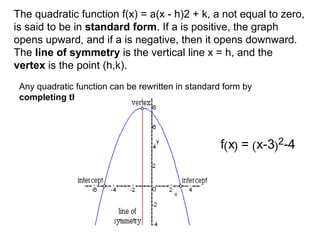
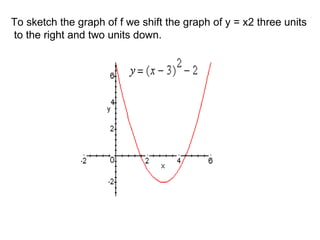
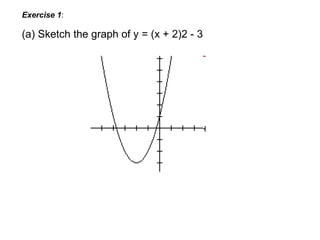
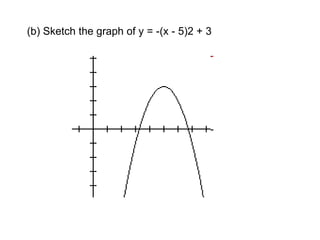
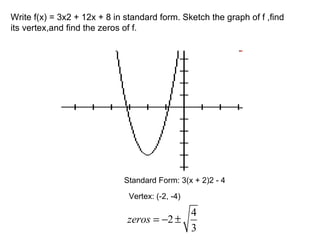
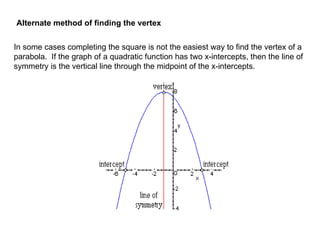
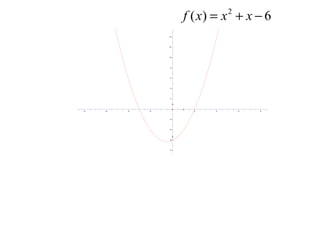
A quadratic function has the form f(x) = ax^2 + bx + c, where a != 0. The graph of a quadratic function is a parabola, which is symmetric around its axis of symmetry. Any quadratic function can be written in standard form by completing the square, where the standard form is f(x) = a(x-h)^2 + k. The vertex of the parabola is the point (h, k) and the line of symmetry is x = h.