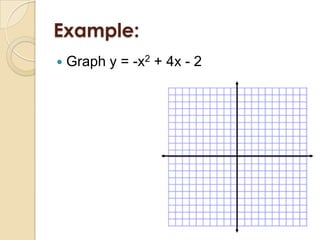
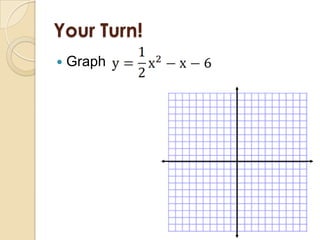
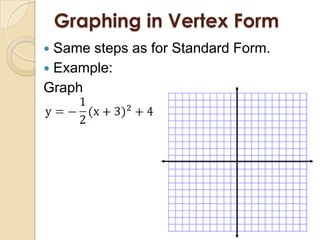
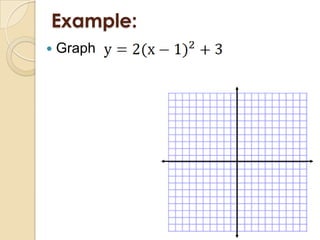
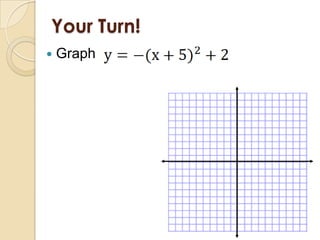
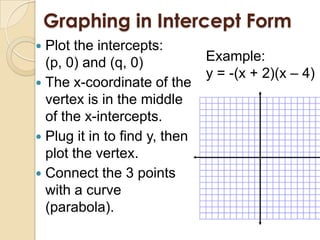
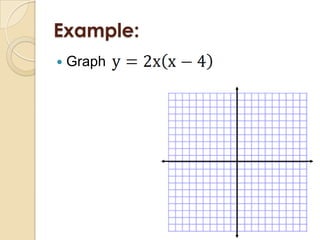
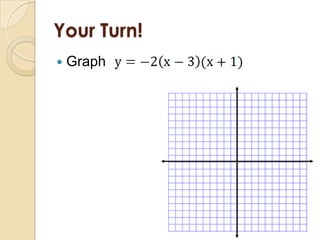
This document discusses graphing quadratic functions. It defines a quadratic function as having the form y = ax^2 + bx + c, where a is not equal to 0. The graph of a quadratic function is a U-shaped parabola. It discusses finding the vertex and axis of symmetry in standard form, vertex form, and intercept form. Examples are provided for graphing quadratic functions written in these three forms.

1. 5.1 Graphing Quadratic
Functions

2. What is a Quadratic Function?
 A function with the form y = ax2 + bx + c
where a 0.
 The graph is U-shaped and is called a
parabola.

3. Why Study Quadratics?
 Many things we see every day are
modeled by quadratic functions.
 What are some examples?
◦ Water in a drinking fountain
◦ The McDonald’s Golden Arches
◦ The path of a basketball

4. Quadratic Vocab
 The lowest or highest point is called the
vertex.
 The axis of symmetry is a vertical line
through the vertex.

5. Effects of “a”
 Standard Form: y = ax2 + bx + c
 Just like with absolute value functions:
◦ If a > 0 (+), the parabola opens up
◦ If a < 0 (-), the parabola opens down
◦ If |a| < 1, the parabola is wider than y = x2
◦ If |a| > 1, the parabola is narrower than
y = x2

6. Finding the Vertex
 The x-coordinate of the vertex is
 To find the y, plug in the x-coordinate.
 Example: Find the vertex.
y = 2x2 – 8x + 6
 Axis of symmetry is the line x =

7. Graphing in Standard Form
 Find and plot the vertex. Example:
 Draw the axis of y = 2x2 – 8x + 6
symmetry.
 Choose two x values on
one side and plot the
points.
 Use symmetry to plot
two points on the other
side.
 Connect the points with
a curve (parabola).

8. Example:
 Graph y = -x2 + 4x - 2

9. Your Turn!
 Graph

10. Vertex Form
 y = a(x – h)2 + k
 The vertex is (h, k)
 Axis of symmetry is x = h.
 Just like absolute value functions:
◦ h shifts right or left
◦ k shifts up or down
◦ a determines direction and width

11. Graphing in Vertex Form
 Same steps as for Standard Form.
 Example:
Graph

12. Example:
 Graph

13. Your Turn!
 Graph

14. Intercept Form
 y = a(x – p)(x – q)
 X-intercepts are p and q
 Axis of symmetry is halfway between
(p, 0) and (q, 0).

15. Graphing in Intercept Form
 Plot the intercepts:
(p, 0) and (q, 0) Example:
y = -(x + 2)(x – 4)
 The x-coordinate of the
vertex is in the middle
of the x-intercepts.
 Plug it in to find y, then
plot the vertex.
 Connect the 3 points
with a curve
(parabola).

16. Example:
 Graph

17. Your Turn!
 Graph

18. Writing in Standard Form
 Multiply! (Use FOIL)
 Example:
 Write in standard form:

19. Example:
 Write in standard form:

20. Your Turn!
 Write in standard form:
 1.
 2.