This document contains notes and materials for a Math 9 class covering quadratic functions for the 6th week of the 1st quarter. It includes: 1. A math prayer to work problems and trust in God's help. 2. An overview of topics to be covered: illustrating quadratic functions, transforming between general and vertex forms, and determining parts of quadratic graphs. 3. A review question asking students to identify which situation represents a quadratic function. 4. Examples of transforming between the general and vertex forms of quadratic functions. 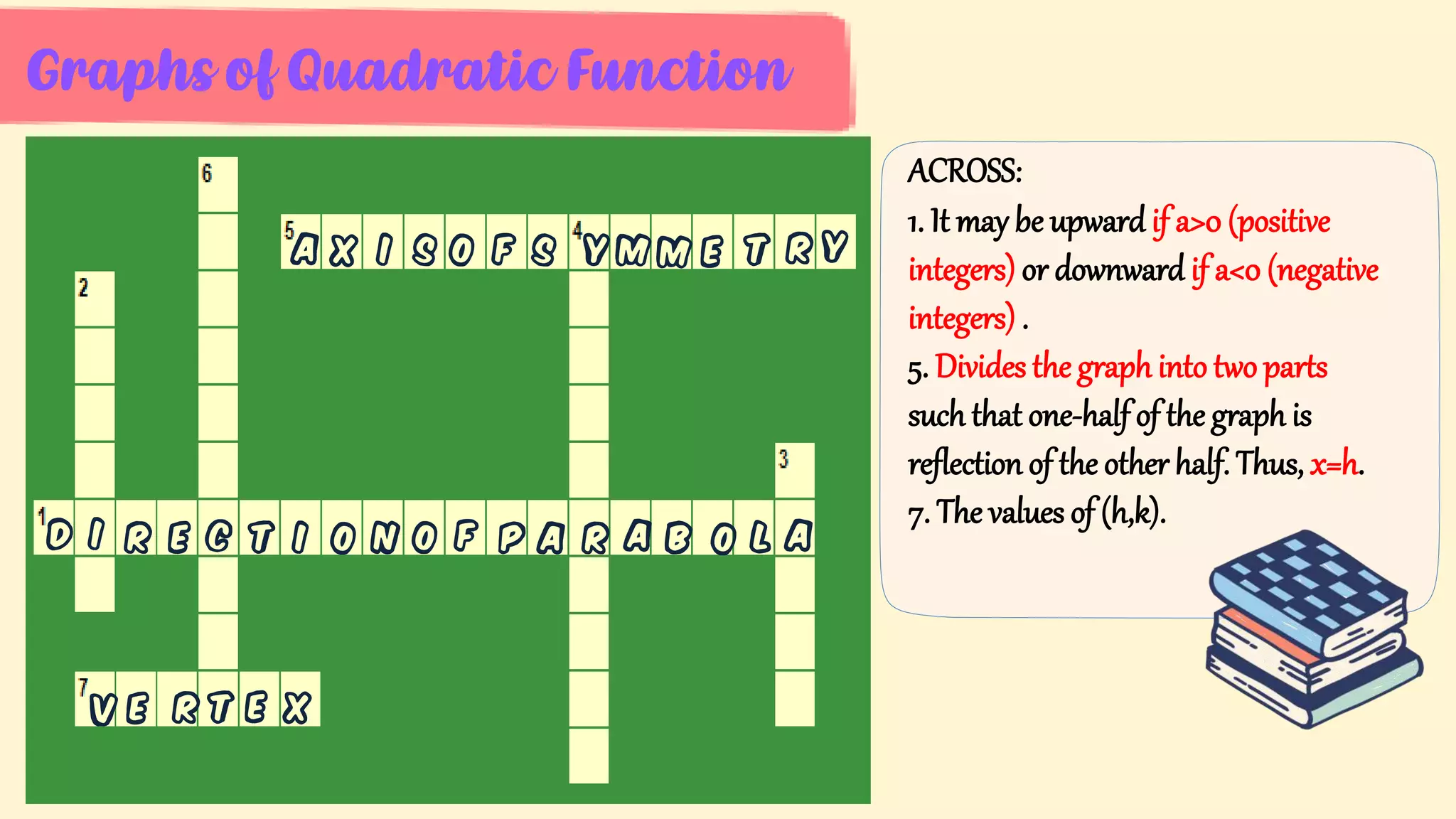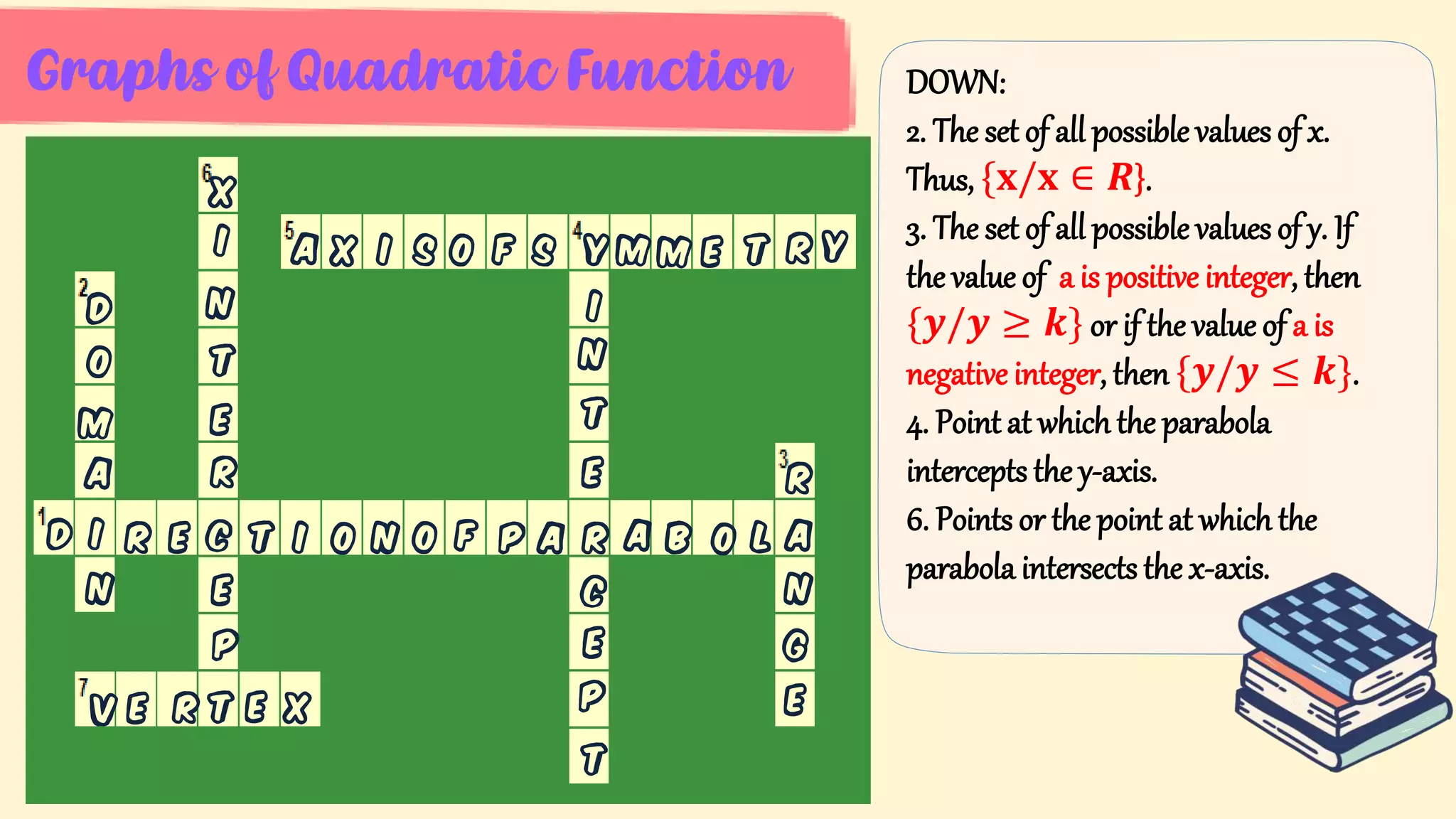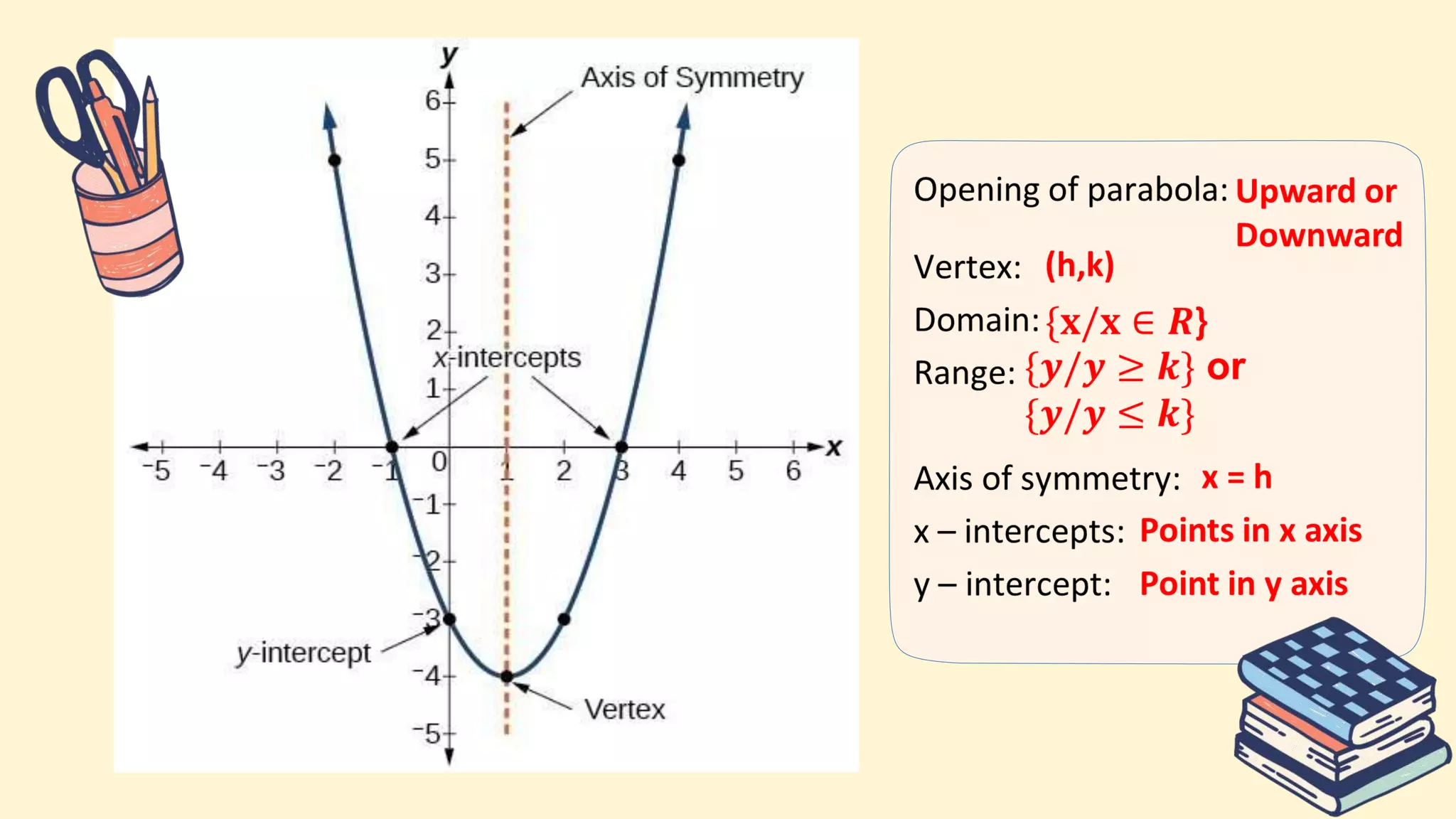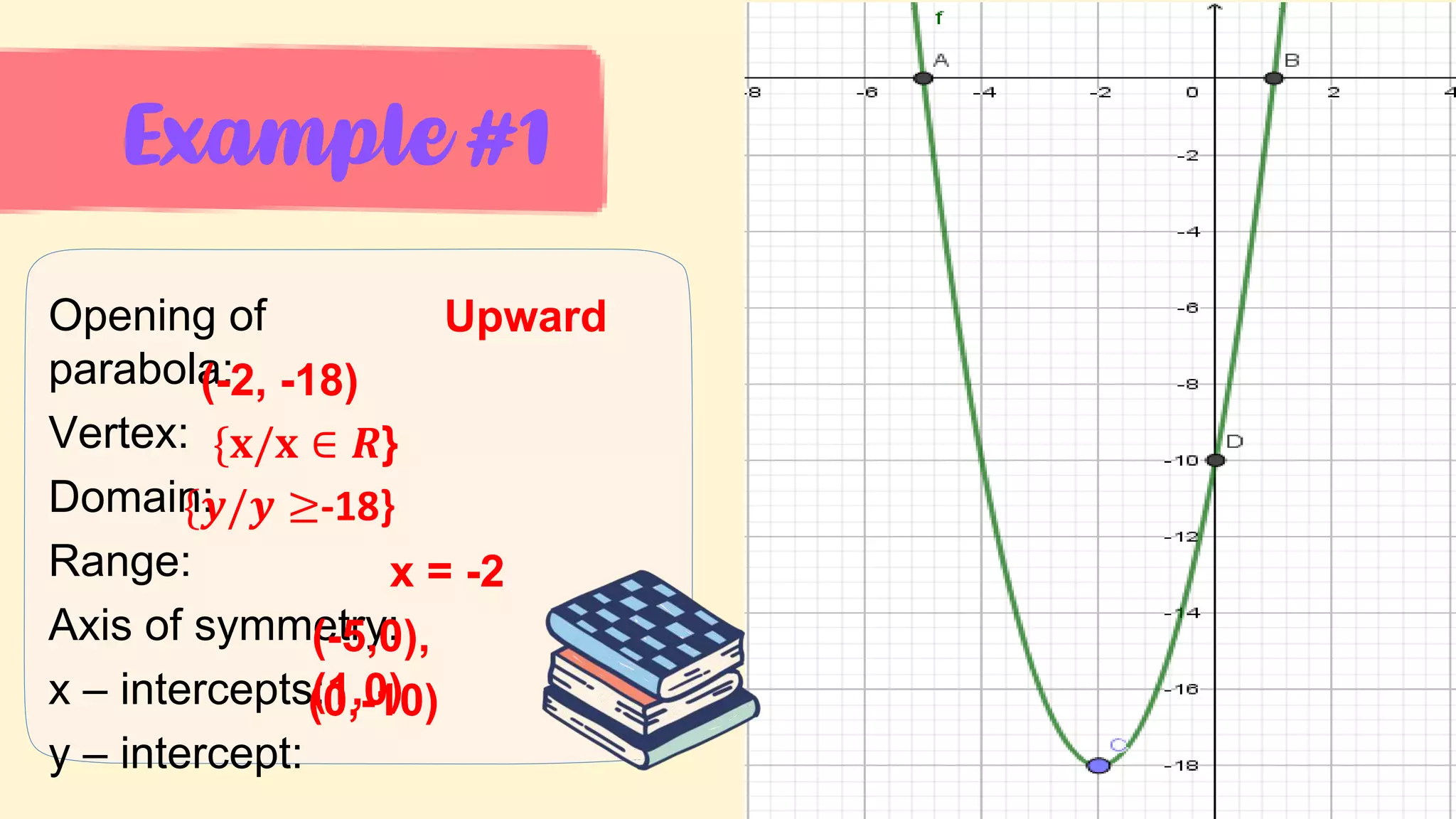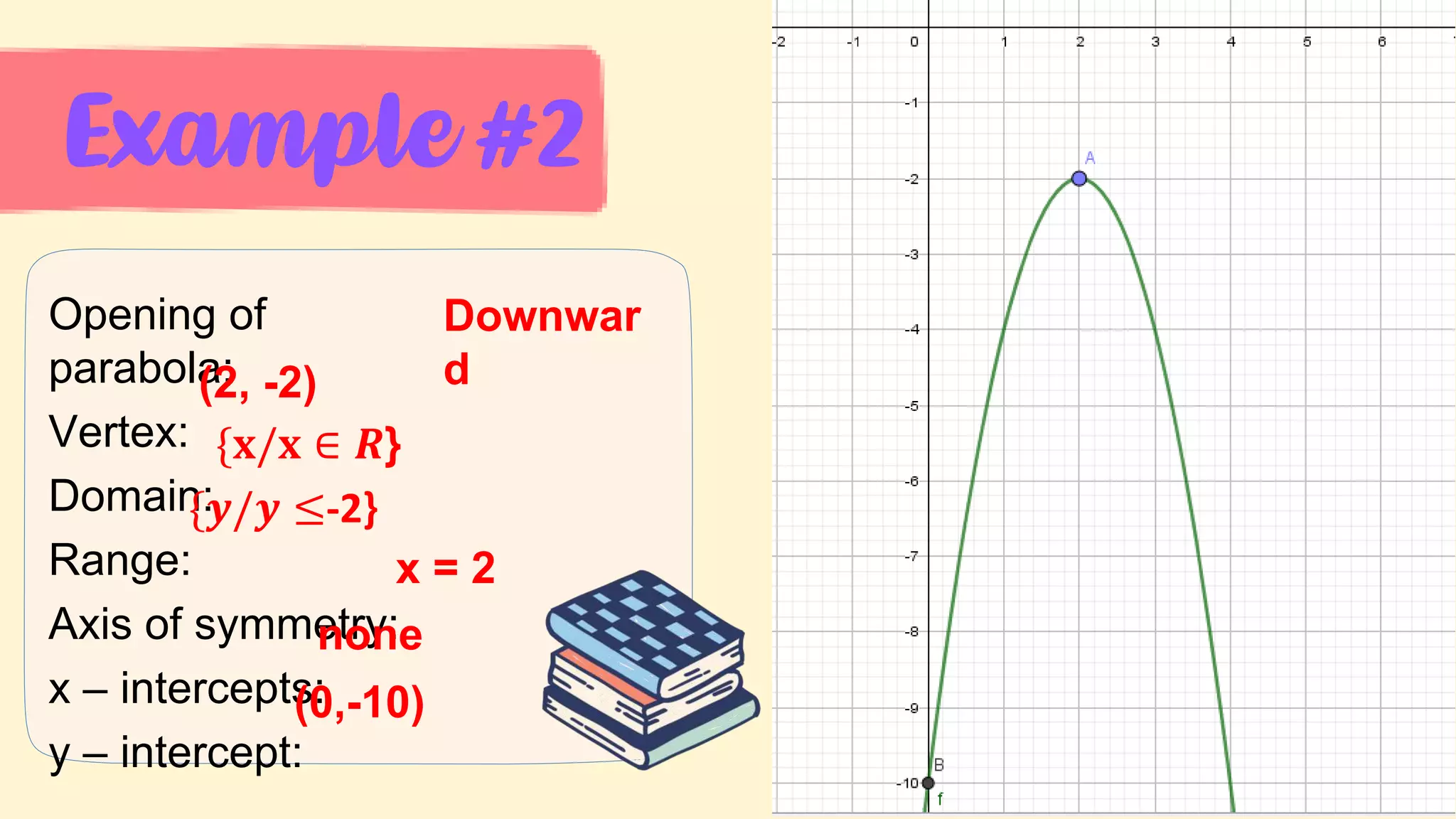5. Key parts of graphs of quadratic functions including the vertex, axis of symmetry, x- and y-intercepts, and the effect of the leading coefficient on

1. Math 9 – Quarter 1 – Week 6

2. Math Prayer
Workout your problem within parenthesis, do not run away.
Put all your trust on God
Exponentially He will do even the most impossible thing
Multiply the joy in your heart, let others experience it too
Divide your loneliness, share it with people around you
Add enthusiasmto realize your dreams, go straight to your plan.
Finally, subtract all the worries and anxieties that you have,
give themall to the Lord and He will carry you
Amen

3. What you’ll learn
a. Illustrate quadratic function,
b. Transformquadratic function in general form into
vertex form and vice versa, and
c. Determine the different parts of the graph of quadratic
function.

4. Review
Which of the following situations
represent the QUADRATIC
FUNCTION? Justify your answer.

6. General form to
Vertex form
𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐
GENERAL FORM
𝑦 = 𝑎(𝑥 − ℎ)2
+𝑘
VERTEX FORM

7. Example #1
a = 3 b = -12 c =
16
𝒚 = 𝒂(𝒙 − 𝒉)𝟐
+𝒌
𝒚 = 𝟑(𝒙 − 𝟐)𝟐
+𝟒
𝒉 =
−𝒃
𝟐𝒂
ℎ =
−(−12)
2(3)
ℎ =
12
6
𝒉 = 𝟐
𝒌 =
𝟒𝒂𝒄 − 𝒃𝟐
𝟒𝒂
k =
4(3)(16) − (−12)2
4(3)
k =
192 − 144
12
k =
48
12
𝒌 = 𝟒
𝒚 = 𝟑𝒙𝟐
− 𝟏𝟐𝒙 + 𝟏𝟔

8. Example #2
𝒂 = 𝟏 𝒃 = 𝟐 𝒄 = −𝟏
𝒚 = 𝒂(𝒙 − 𝒉)𝟐
+𝒌
𝒚 = (𝒙 + 𝟏)𝟐
−𝟐
𝒉 =
−𝒃
𝟐𝒂
ℎ =
−(2)
2(1)
ℎ =
−2
2
𝒉 = −𝟏
𝒌 =
𝟒𝒂𝒄 − 𝒃𝟐
𝟒𝒂
k =
4(1)(−1) − (2)2
4(1)
k =
−4 − 4
4
k =
−8
4
𝒌 = −𝟐
𝒚 = 𝒙𝟐
+ 𝟐𝒙 − 𝟏

9. Vertex form to
General form
𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐
GENERAL FORM
𝑦 = 𝑎(𝑥 − ℎ)2
+𝑘
VERTEX FORM

10. Example #1
𝒚 = 𝟑(𝒙 − 𝟐)𝟐
+𝟒
𝒚 = 𝟑(𝒙 − 𝟐)𝟐
+𝟒
𝒚 = 𝟑 𝒙𝟐
− 𝟒𝐱 + 𝟒 + 𝟒
𝒚 = 𝟑𝒙𝟐
− 𝟏𝟐𝐱 + 𝟏𝟐 + 𝟒
𝒚 = 𝟑𝒙𝟐
− 𝟏𝟐𝐱 + 𝟏𝟔

11. Example #2
𝒚 = (𝒙 + 𝟏)𝟐
−𝟐
𝒚 = (𝒙 + 𝟏)𝟐
−𝟐
𝒚 = 𝒙𝟐
+ 𝟐𝐱 + 𝟏 − 𝟐
𝒚 = 𝒙𝟐
+ 𝟐𝐱 − 𝟏

12. Graphs of Quadratic Function
ACROSS:
1. It may be upward if a>0 (positive
integers) or downward if a<0 (negative
integers) .
5. Divides the graph into two parts
such that one-half of the graph is
reflection of the other half. Thus, x=h.
7. The values of (h,k).
V e r T E X
t
D I r e c T I O N O F p A r A B O L A
a x i s f s y m m e r Y
O

13. Graphs of Quadratic Function DOWN:
2. The set of all possible values of x.
Thus, {𝐱/𝐱 ∈ 𝑹}.
3. The set of all possible values of y. If
the value of a is positive integer, then
{𝒚/𝒚 ≥ 𝒌} or if the value of a is
negative integer, then {𝒚/𝒚 ≤ 𝒌}.
4. Point at which the parabola
intercepts the y-axis.
6. Points or the point at which the
parabola intersects the x-axis.
V e r T E X
D
O
M
A
I
N
x
n
t
e
c
e
p
t
D I r e c T I O N O F p A r A B O L A
a x i s f s y m m e r Y
I
n
O
r
n
G
e
t
t
e
e
p
r

14. Graphs of
Quadratic Function
Parabola opens UPWARD if a>0 (positive integers)
Parabola opens DOWNWARD if a<0 (negative integers)
values of h and k or (h,k)

15. The set of all possible values of x. Thus, {𝐱/𝐱 ∈ 𝑹}
The set of all possible values of y. If the value of a is
positive integer, then {𝒚/𝒚 ≥ 𝒌} or if the value of a
is negative integer, then {𝒚/𝒚 ≤ 𝒌}
Divides the graph into two parts such that one-half
of the graph is reflection of the other half. Thus, x=h

16. Points or the point at which the parabola intersects
the x-axis. A parabola can have either 2,1 or zero
real x intercepts.
Point at which the parabola intercepts the y-axis

18. Example #1
Opening of
parabola:
Vertex:
Domain:
Range:
Axis of symmetry:
x – intercepts:
y – intercept:
(-2, -18)
Upward
(-5,0),
(1,0)
(0,-10)
x = -2
{𝐱/𝐱 ∈ 𝑹}
{𝒚/𝒚 ≥-18}

19. Example #2
Opening of
parabola:
Vertex:
Domain:
Range:
Axis of symmetry:
x – intercepts:
y – intercept:
(2, -2)
Downwar
d
none
(0,-10)
x = 2
{𝐱/𝐱 ∈ 𝑹}
{𝒚/𝒚 ≤-2}

20. Try this:
Jung Ho Yeon decided to play
badminton at Imus plaza
after attending the mass in
Imus Cathedral. As she hits
the shuttle cock, it forms a
parabola. Based on the
parabola formed write
GREEN LIGHT if the given
statement is true and RED
LIGHT if it is false.

21. 1. The opening of the parabola is downward.
RED LIGHT
2. The vertex of the parabola is (2,1).
GREEN LIGHT
3. The range of the parabola is {𝒚/𝒚 ≥ 𝟏}.
RED LIGHT
4. The axis of symmetry of the parabola is 𝒙 = 𝟐.
RED LIGHT
5. There are no x – intercept in the given graph.
GREEN LIGHT
6. The y – intercept of the parabola is only (-3, -1)
RED LIGHT
7. The equation in vertex form of the given
parabola is 𝑦 = −2(𝑥 + 2)2
+ 1. Hence, its
general form is 𝑦 = −2𝑥2
− 4𝑥 + 1.
RED LIGHT

22. Activity no. 6

23. Reminders:
Check your messenger and google
classroom for your activities
Submit your activities on time
1
2
3 Keep your self updated