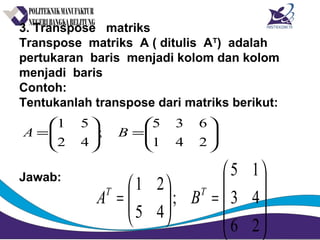
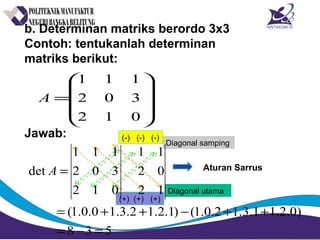
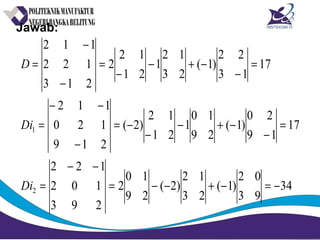
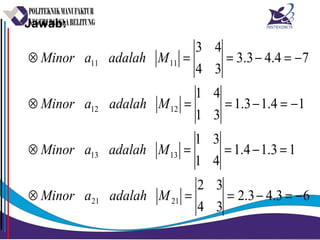
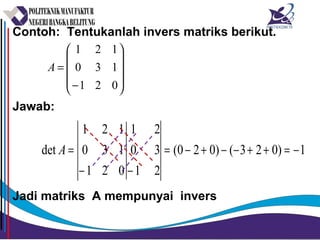
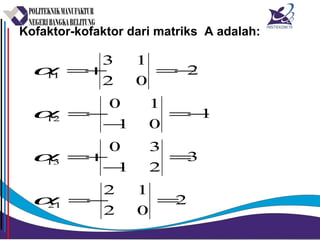
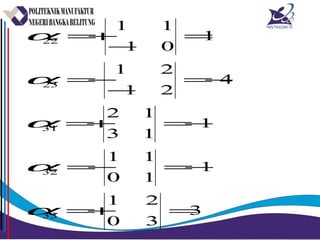
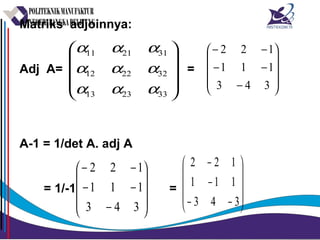
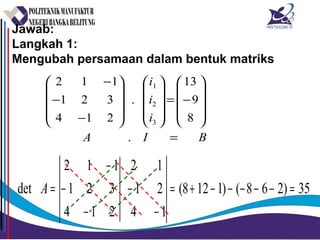
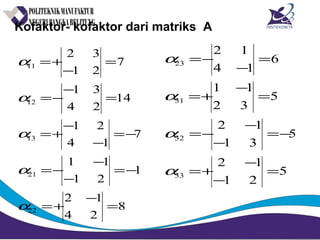
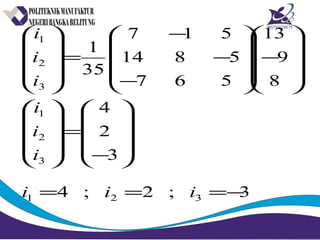
Matriks adalah susunan bilangan dalam bentuk persegi panjang yang diatur menurut baris dan kolom. Matriks dapat dijumlahkan, dikurangkan, dikalikan, dan ditemukan inversnya jika memenuhi syarat tertentu. Determinan dan minor digunakan untuk menghitung invers matriks.