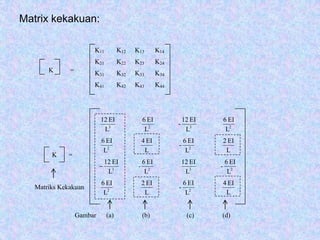
![ANALISA STRUKTUR METODE
MATRIKS
• Analisa Struktur Metode Matriks (ASMM) adalah suatu
metode untuk menganalisa struktur dengan
menggunakan bantuan matriks, yang terdiri dari : matriks
kekakuan, matriks perpindahan, dan matriks gaya.
Dengan menggunakan hubungan :
{ P } = [ K ] { U }
dimana :
{ P } = matriks gaya
[ K ] = matriks kekakuan
{ U } = matriks perpindahan
• Salah satu cara yang digunakan untuk menyelesaikan
persamaan di atas, yaitu dengan menggunakan Metode
Kekakuan.](https://image.slidesharecdn.com/analisamatriks-160620032238/85/Analisa-matriks-1-320.jpg)
Recommended
More Related Content
What's hot
What's hot (20)
Similar to Analisa matriks
Similar to Analisa matriks (20)
Recently uploaded
Recently uploaded (10)
Analisa matriks
- 1. ANALISA STRUKTUR METODE MATRIKS • Analisa Struktur Metode Matriks (ASMM) adalah suatu metode untuk menganalisa struktur dengan menggunakan bantuan matriks, yang terdiri dari : matriks kekakuan, matriks perpindahan, dan matriks gaya. Dengan menggunakan hubungan : { P } = [ K ] { U } dimana : { P } = matriks gaya [ K ] = matriks kekakuan { U } = matriks perpindahan • Salah satu cara yang digunakan untuk menyelesaikan persamaan di atas, yaitu dengan menggunakan Metode Kekakuan.
- 2. • Pada Metode Kekakuan, variable yang tidak diketahui besarnya adalah : perpindahan titik simpul struktur (rotasi dan defleksi) sudah tertentu/pasti. Jadi jumlah variable dalam metode kekakuan sama dengan derajat ketidaktentuan kinematis struktur. • Metode Kekakuan dikembangkan dari persamaan kesetimbangan titik simpul yang ditulis dalam : “ Koefisien Kekakuan “ dan “ Perpindahan titik simpul yang tidak diketahui “.
- 3. Types of Elements Spring elements Truss elements (plane & 3D) Beam elements (2D &3D) Plane Frame Grid elements Plane Stress Plane Strain Axisymmetric elements Plate Shell
- 4. Degrees of Freedom (DOF) • Derajat kebebasan yang dimiliki oleh suatu struktur. • Tiap jenis elemen akan mempunyai jumlah dan jenis kebebasan tertentu. Hitung derajat kebebasan element dari jenis element yang disebutkan sebelumnya
- 5. Metode Kekakuan Langsung (Direct Stiffness Method) matriks kekakuan U1, P1 U2, P2 { P } = [ K ] { U } U3, P3 U4, P4 gaya perpindahan P1 K11 K12 K13 K14 U1 P2 K21 K22 K23 K24 U2 P3 K31 K32 K33 K34 U3 P4 K41 K42 K43 K44 U4 1 1 2 =
- 6. P1 = K11 . U1 + K12 . U2 + K13 . U3 + K14 . U4 Kesetimbangan gaya di arah U1 P2 = K21 . U1 + K22 . U2 + K23 . U3 + K24 . U4 Kesetimbangan gaya di arah U2 P3 = K31 . U1 + K32 . U2 + K33 . U3 + K34 . U4 Kesetimbangan gaya di arah U3 P4 = K41 . U1 + K42 . U2 + K43 . U3 + K44 . U4 Kesetimbangan gaya di arah U4
- 7. • Jika U1 = 1 dan U2 = U3 = U4 = 0 , maka : P1 = K11 ; P2 = K21 ; P3 = K31 ; P4 = K41 Lihat Gambar (a) • Jika U2 = 1 dan U2 = U3 = U4 = 0 , maka : P1 = K12 ; P2 = K22 ; P3 = K32 ; P4 = K42 Lihat Gambar (b) • Jika U3 = 1 dan U2 = U3 = U4 = 0 , maka : P1 = K13 ; P2 = K23 ; P3 = K33 ; P4 = K43 Lihat Gambar (c) • Jika U4 = 1 dan U2 = U3 = U4 = 0 , maka : P1 = K14 ; P2 = K24 ; P3 = K34 ; P4 = K44 Lihat Gambar (d)
- 8. U1’ = 1 P1’ = K11 P2’ = K21 P3’ = K31 P4’ = K41 U1’ = 1 P1’ = K11 P2’ = K21 P3’ = K31 P4’ = K41 U1’ = 1 P1’ = K11 P2’ = K21 P3’ = K31 P4’ = K41 U1’ = 1 P1’ = K11 P2’ = K21 P3’ = K31 P4’ = K41
- 9. Matrix kekakuan: K11 K12 K13 K14 K21 K22 K23 K24 K31 K32 K33 K34 K41 K42 K43 K44 2323 L EI6 L EI12 - L EI6 L EI12 L EI2 L EI6 - L EI4 L EI6 22 2323 L EI6 - L EI12 L EI6 L EI12 -− Matriks Kekakuan L EI4 L EI6 - L EI2 L EI6 22 Gambar (a) (b) (c) (d) K = K =
- 10. Jika pada batang bekerja gaya aksial : L, EA K11 = L EA K21 = L EA − U1, P1 U2, P2 U3, P3 U4, P4 U1’,P1’ U2’,P2’ U1’= 1 K12 = - L EA U2’= 1 K22 = L EA 1 1 2 Matriks kekakuan elemen dengan melibatkan gaya aksial : 6 x 6 K = 2323 L EI6 L EI12 -0 L EI6 L EI12 0 L EI2 L EI6 -0 L EI4 L EI6 0 22 2323 L EI6 - L EI12 0 L EI6 L EI12 0 -− L EI4 L EI6 -0 L EI2 L EI6 0 22 00 L EA -00 L EA 00 L EA -00 L EA −
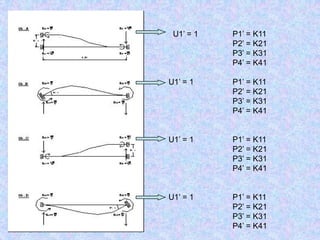
- 11. Contoh q Sebuah balok statis tak tentu seperti pada gambar 1 1 2 2 3 L, EI L, EI Menentukan keaktifan ujung-ujung elemen Menentukan matriks tujuan DOF : 2 2 rotasi Matriks kekakuan struktur [ Ks ] 2 x 2 Membuat matrik kekakuan elemen : [ Ks ] = [ K1 ] + [ K2 ] 1 2 3 0 1 2 0 0 0 1 2 1 2 3 0 0 0 1 2 0 1 1 2 0
- 12. Membuat matrik kekakuan elemen : Elemen 1 0 0 0 1 2323 L EI6 L EI12 - L EI6 L EI12 0 L EI2 L EI6 - L EI4 L EI6 22 0 2323 L EI6 - L EI12 L EI6 L EI12 -− 0 L EI4 L EI6 - L EI2 L EI6 22 1 K1 = [ K1 ] = Matriks Tujuan { T1 } = { 0 0 0 1 }T 0 L EI4 2 x 2 0 0
- 13. Elemen 2 0 1 0 2 2323 L EI6 L EI12 - L EI6 L EI12 0 L EI2 L EI6 - L EI4 L EI6 22 1 2323 L EI6 - L EI12 L EI6 L EI12 -− 0 L EI4 L EI6 - L EI2 L EI6 22 2 Matriks Tujuan { T2 } = { 0 1 0 2 }T 2 x 2 K2 = [ K2 ] = L EI4 L EI2 L EI2 L EI4
- 14. = + 0 0 = Matriks Kekakuan Global Struktur [ Ks ] = [ K1 ] + [ K2 ] [ Ks ] 2 x 2 L EI4 L EI2 L EI2 L EI4 0 L EI4 L EI4 L EI2 L EI2 L EI8 Untuk mendapatkan deformasi ujung-ujung aktif struktur, maka digunakan hubungan : { Ps } = [ Ks ] { Us } { Us } = [ Ks ]-1 { Ps } dimana : Us = deformasi ujung-ujung aktif Ks = kekakuan struktur Ps = gaya-gaya pada ujung aktif elemen akibat beban luar (aksi)
- 15. q 0 0 Untuk contoh di atas, maka : Ps = Menghitung invers matrik kekakuan global [ Ks ]-1 [ Ks ] = [ Ks ]-1 = 82- 2-4 EI L 2.2-4.8 1 = 82- 2-4 EI28 L Jadi : { Us } = [ Ks ]-1 { Ps } Us = 82- 2-4 EI28 L 2 Lq 12 1 − 2 Lq 12 1 L EI4 L EI2 L EI2 L EI8 2 Lq 12 1 − 2 Lq 12 1 2 Lq 12 1 − 2 Lq 12 1
- 16. U1 1 U1 2 U1 3 U1 4 0 0 0 U2 1 U2 2 U2 3 U2 4 0 0 Us = EI28 L Us = Deformasi untuk masing-masing elemen Elemen 1 : U1 = = Elemen 2 : U2 = = 22 Lq 6 1 -Lq 3 1 − 22 Lq 6 4 Lq 6 1 + EI Lq 168 3 3 − EI Lq 168 5 3 Rotasi di joint 2 Rotasi di joint 3 EI Lq 168 3 3 − EI Lq 168 3 3 − EI Lq 168 5 3
- 17. q 0 0 0 0 0 0 PR2 =PR1 = Reaksi akibat beban luar : 2 Lq 12 1 −2 Lq 12 1 2 Lq 2 Lq 2 Lq 12 1 − 2 Lq 12 1 2 Lq 2 Lq
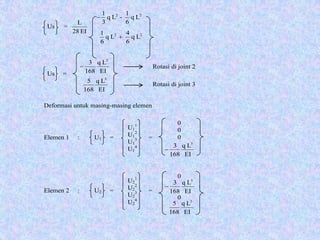
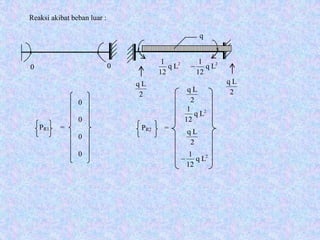
- 18. 0 0 0 0 0 0 0 Gaya akhir elemen : Elemen 1 : { P1 } = [ K1 ] + { PR1 } P1 = + P1 = = 2323 L EI6 L EI12 - L EI6 L EI12 L EI2 L EI6 - L EI4 L EI6 22 2323 L EI6 - L EI12 L EI6 L EI12 -− L EI4 L EI6 - L EI2 L EI6 22 EI Lq 168 3 3 − 2 Lq 56 4 − 2 Lq 56 2 − Lq 56 6 − Lq 56 6 2 Lq 28 2 − 2 Lq 28 1 − Lq 28 3 − Lq 28 3
- 19. 0 0 0 0 Elemen 2 : { P2 } = [ K2 ] + { PR2 } P2 = + P2 = = 2323 L EI6 L EI12 - L EI6 L EI12 L EI2 L EI6 - L EI4 L EI6 22 2323 L EI6 - L EI12 L EI6 L EI12 -− L EI4 L EI6 - L EI2 L EI6 22 EI Lq 168 5 3 2 Lq 56 4 Lq 56 32 Lq 56 24 2 Lq 28 2 Lq 28 16 Lq 28 12 EI Lq 168 3 3 − 2 Lq 12 1 − 2 Lq 12 1 2 Lq 2 Lq
- 20. q 0 - - + - + + Free Body Diagram : Menggambar gaya-gaya dalam : Bidang D : Bidang M : 2 Lq 28 22 Lq 28 1 Lq 28 3 2 Lq 28 2 Lq 28 16 Lq 28 3 Lq 28 12 Lq 28 3 Lq 28 3 Lq 28 16 Lq 28 12 2 Lq 28 2 2 Lq 28 1
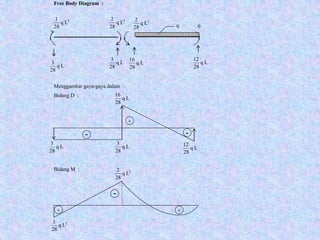
- 21. Elemen Portal 2D B C P EI EI L L/2L/2 A A B C 1 2 DOF = 2 0 1 1 2 Sebuah portal statis tak tentu seperti pada gambar Matriks kekakuan struktur [ Ks ] 2 x 2 [ Ks ] = [ K1 ] + [ K2 ]
- 22. [ K1 ] = 0 0 0 Elemen 1 0 1 0 2 x 2 1 Matriks Tujuan { T1 } = { 0 1 }T 2 x 2 Elemen 2 1 2 1 2 x 2 2 Matriks Tujuan { T2 } = { 1 2 }T 2 x 2 K1 = [ K2 ] = L EI4 L EI2 L EI2 L EI4 L EI2 L EI4 L EI4 L EI2 L EI4 K2 = L EI2 L EI4 L EI4 L EI2
- 23. = + 0 = 0 0 Matriks Kekakuan Global Struktur [ Ks ] = [ K1 ] + [ K2 ] [ Ks ] 2 x 2 Untuk mendapatkan deformasi ujung-ujung aktif struktur, maka digunakan hubungan : { Ps } = [ Ks ] { Us } { Us } = [ Ks ]-1 { Ps } dimana : Us = deformasi ujung-ujung aktif Ks = kekakuan struktur Ps = gaya-gaya pada ujung aktif elemen akibat beban luar (aksi) L EI4 L EI2 L EI2 L EI4 L EI4 L EI2 L EI2 L EI8 L EI4
- 24. P Untuk contoh di atas, maka : 0 0 Ps = Menghitung invers matrik kekakuan global [ Ks ]-1 [ Ks ] = [ Ks ]-1 = 82- 2-4 EI L 2.2-4.8 1 = 82- 2-4 EI28 L LP 8 1 − LP 8 1 L EI4 L EI2 L EI2 L EI8 LP 8 1 − LP 8 1
- 25. Jadi : { Us } = [ Ks ]-1 { Ps } Us = 82- 2-4 EI28 L Us = EI28 L Us = LP 8 1 − LP 8 1 22 Lq 6 1 -Lq 3 1 − 22 Lq 6 4 Lq 6 1 + EI LP 112 3 2 − EI LP 112 5 2 Rotasi di joint B Rotasi di joint C U1 1 U1 2 0 U2 1 U2 2 Deformasi untuk masing-masing elemen Elemen 1 : U1 = = Elemen 2 : U2 = = EI LP 112 3 2 − EI LP 112 3 2 − EI LP 112 5 2
- 26. P Reaksi akibat beban luar : 0 0 LP 8 1 −LP 8 1 0 PR1 = 0 PR2 = LP 8 1 − LP 8 1 0 0 0 P1 = + P1 = Hasil perhitungan hanya momen saja Gaya akhir elemen : Elemen 1 : { P1 } = [ K1 ] + { PR1 } EI LP 112 3 2 − LP 56 6 − LP 56 3 − L EI2 L EI4 L EI4 L EI2 P2 = + P2 = = 0 0 Hasil perhitungan hanya momen saja Elemen 2 : { P2 } = [ K2 ] + { PR2 } EI LP 112 5 2 LP 8 1 − LP 8 1 EI LP 112 3 2 − L EI2 L EI4 L EI4 L EI2 2 Lq 56 6 2 Lq 28 3
- 27. P 0 Dihitung lagi Dihitung lagi Free Body Diagram : P 56 9 LP 56 6 P 28 17 P 28 11 P 56 9 P 56 9 P 56 9 P 28 17 P 28 17 LP 56 6 LP 56 3 Bidang M : - - + LP 56 6 LP 56 3 LP 56 11 + Bidang D : Bidang N : - +P 28 17 - P 56 9 P 28 11 P P 28 17 - P 56 9 -
- 28. Transformasi Sumbu θ 1 2’ 2 3 1’ 3’ U3, P3 u3, p3 U1, P1 U2, P2 u1, p1 u2, p2 u1 u2 u3 = C S 0 -S C 0 0 0 1 U1 U2 U3 C = cos θ S = sin θ Koordinat Lokal dan Global
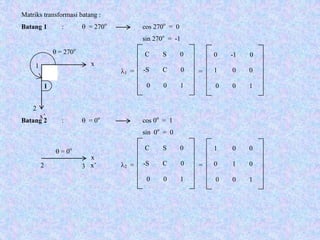
- 29. C S 0 -S C 0 0 0 1 C = cos θ S = sin θ u1 u2 u3 u4 u5 u6 = λ 0 0 λ U1 U2 U3 U4 U5 U6 [ u ] = [ R ] [ U ] R = matriks rotasi Atau dapat ditulis : u = λ U Dimana : λ = Untuk transformasi sumbu sebuah titik dengan 6 dof dapat ditulis :
- 30. P1 P2 P3 P4 P5 P6 = λΤ 0 0 λΤ p1 p2 p3 p4 p5 p6 [ P ] = [ R ]T [ p ] R = matriks rotasi K Transformasi sumbu juga berlaku untuk gaya : p = λ P P = λ-1 p λ-1 = λT P = λT p p = k u ; u = R U P = RT p P = K U = RT k u K = RT k R = RT k R U
- 31. Matriks kekakuan elemen untuk 6 dof : 6 x 6 k = 2323 L EI6 L EI12 -0 L EI6 L EI12 0 L EI2 L EI6 -0 L EI4 L EI6 0 22 2323 L EI6 - L EI12 0 L EI6 L EI12 0 -− L EI4 L EI6 -0 L EI2 L EI6 0 22 00 L EA -00 L EA 00 L EA -00 L EA − β 0 0 -β 0 0 0 12 6L 0 -12 6L 0 6L 4L2 0 -6L 2L2 -β 0 0 β 0 0 0 -12 -6L 0 12 -6L 0 6L 2L2 0 -6L 4L2 Dimana : α = β = [ K ] = [ R ]T [ k ] [ R ] k = α L EI 3 I LA 2
- 32. C -S 0 S C 0 0 0 1 C -S 0 S C 0 0 0 1 0 0 β 0 0 -β 0 0 0 12 6L 0 -12 6L 0 6L 4L2 0 -6L 2L2 -β 0 0 β 0 0 0 -12 -6L 0 12 -6L 0 6L 2L2 0 -6L 4L2 K = α C S 0 -S C 0 0 0 1 C S 0 -S C 0 0 0 1 0 0 g1 g2 g4 -g1 -g2 g4 g3 g5 -g2 -g3 g5 g6 -g4 -g5 g7 g1 g2 -g4 g3 -g5 g6 Dimana : g1 = α ( β C2 + 12 S2 ) g5 = α 6 L C g2 = α C S ( β - 12 ) g6 = α 4 L2 g3 = α ( β S2 + 12 C2 ) g7 = α 2 L2 g4 = -α 6 L S K =
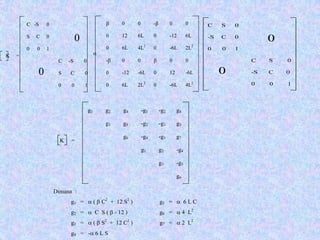
- 33. Sebuah portal seperti gambar, dengan menggunakan transformasi sumbu hitunglah gaya-gaya dalam yang bekerja q = 1,68 k/ft L = 10 ft M = 14 kft = 168 kin L = 10 ft 1 2 3 1 2 E = 30.000 ksi A = 5 in2 I = 50 in4 L = 10 ft 1 2 1 2 3 0 0 3 1 0 0 2 0 0 Sumbu Global DOF [ Ks ] 3 x 3 1 2 1 2 3 2 4 5 4 5 6 13 Sumbu Lokal DOF [ k ] 3 x 3 6 1 3 2 2
- 34. 1 2 x x’ 1 θ = 270o λ1 = C S 0 -S C 0 0 0 1 = 0 -1 0 1 0 0 0 0 1 2 3 x x’ θ = 0o λ2 = C S 0 -S C 0 0 0 1 = 1 0 0 0 1 0 0 0 1 Matriks transformasi batang : Batang 1 : θ = 270o cos 270o = 0 sin 270o = -1 Batang 2 : θ = 0o cos 0o = 1 sin 0o = 0
- 35. C S 0 -S C 0 0 0 1 C S 0 -S C 0 0 0 1 0 0 0 -1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 -1 0 0 0 0 1 0 0 0 0 0 0 0 1 C S 0 -S C 0 0 0 1 C S 0 -S C 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 R1 = = R2 = =
- 36. g1 g2 g4 -g1 -g2 g4 g3 g5 -g2 -g3 g5 g6 -g4 -g5 g7 g1 g2 -g4 g3 -g5 -g4 g6 0 0 0 1 0 2 Matriks kekakuan system struktur Elemen 1 : α1 = 33 1 12).10( 50.30.000 L EI = = 0,87 β1 = 50 12).(10.5 I LA 22 1 = = 1.440 C = 0 ; S = -1 { T } = { 0 0 0 1 0 2 }T 0 0 0 1 0 2 K1 = g1 -g4 0 -g4 g6 0 0 0 0 1 2 3 10,44 -626,4 0 -626,4 50.112 0 0 0 0 1 2 3 g1 = α ( β C2 + 12 S2 ) = 0,87 [ 0 + 12 (-1)2 ] = 10,44 g4 = -α 6 L S = -0,87 . 6 . 120 (-1) = 626,4 g6 = α 4 L2 = 0,87 . 4 . 1202 = 50.112 Sehingga : K1 = K1 =
- 37. g1 g2 g4 -g1 -g2 g4 g3 g5 -g2 -g3 g5 g4 g6 -g4 -g5 g7 g1 g2 -g4 g3 -g5 g4 g7 g6 1 0 2 0 0 3 g1 g4 g4 g4 g6 g7 g4 g7 g6 1 2 3 Elemen 2 : α2 = 33 1 12).10( 50.30.000 L EI = = 0,87 β2 = 50 12).(10.5 I LA 22 1 = = 1.440 C = 1 ; S = 0 { T } = { 1 0 2 0 0 3 }T 1 0 2 0 0 3 1 2 3 K2 = K2 = 1.252,8 0 0 0 50.112 25.056 0 25.056 50.112 1.263,24 -626,4 0 -626,4 100.224 25.056 0 25.056 50.112 g1 = α ( β C2 + 12 S2 ) = 0,87 [ 1.440 . 12 + 12 (0)2 ] = 1.252,8 g4 = -α 6 L S = -0,87 . 6 . 120 (0) = 0 g6 = α 4 L2 = 0,87 . 4 . 1202 = 50.112 g7 = α 2 L2 = 0,87 . 2 . 1202 = 25.056 Sehingga : KS = K2 =
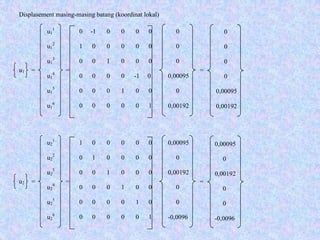
- 38. q = 0,14 k/in 168 kin168 kin168 kin 0 0 0 168 0 1.263,24 -626,4 0 -626,4 100.224 25.056 0 25.056 50.112 - 1 0 168 0 0,00095 0,00192 -0,00096 Defleksi horizontal di 2 Rotasi di 2 Rotasi di 3 Matriks beban : 8,4 8,4 PS = { Ps } = [ Ks ] { Us } { Us } = [ Ks ]-1 { Ps } US = US =
- 39. u1 1 u1 2 u1 3 u1 4 u1 5 u1 6 0 0 0 0,00095 0 0,00192 = 0 0 0 0 0,00095 0,00192 u2 1 u2 2 u2 3 u2 4 u2 5 u2 6 0,00095 0 0,00192 0 0 -0,0096 = 0,00095 0 0,00192 0 0 -0,0096 Displasement masing-masing batang (koordinat lokal) u1 = = u2 = = 0 -1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 -1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1
- 40. 0 1,193 k 47,512 kin 0 -1,193 k 95,620 kin 0 1,193 k 3,959 kft 0 -1,193 k 7,968 kft Gaya akhir batang : Elemen 1 : { P1 } = [ k1 ] { u1 } + { 0 } P1 = = 1,19 k -7,8 k -95,84 kin -1,19 k -9 k 168 kin 1,19 k -7,8 k -7,99 kft -1,19 k -9 k 14 kft Elemen 2 : { P2 } = [ k2 ] { u2 } + { Faksi } P2 = =
- 41. q = 1,68 k/ft 14 kft 7,8 k 9 k 1 2 1,19 k1,19 k 7,99 kft 1,193 k 1,193 k 0 3,959 7,968 kft Free body diagram : 3,959 + - 7,99 14 + + - + + - 1,193 1,193 7,8 9 - 1,191,19
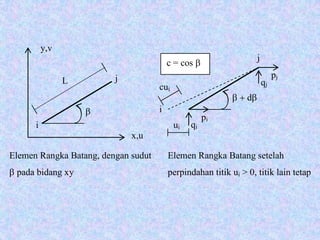
- 42. KONSTRUKSI RANGKA BATANG • Pada Konstruksi Rangka Batang (KRB), perhitungan matriks kekakuan elemen [ K ] berdasarkan kasus rangka batang 2 Dimensi. Gaya yang bekerja hanya tarik dan tekan aksial saja, sedang gaya momen dan lintang tidak terjadi. • Perhatikan gambar dengan elemen struktur batang dengan luas A dan Modulus Elastisitas E konstan. Perhitungan kekakuan elemen hanya mengandung elemen A, E dan empat titik koordinat, yaitu : xi, xj, yi, dan yj.
- 43. β x,u y,v L i j β + dβ i j cui ui qi pi qj pj Elemen Rangka Batang, dengan sudut Elemen Rangka Batang setelah β pada bidang xy perpindahan titik ui > 0, titik lain tetap c = cos β
- 44. C2 CS -C2 -CS ui = pi qi pj qj Pertama, harus menghitung : L = ( ) ( )2 ij 2 ij y-yx-x + C = cos β = L x-x ij S = sin β = L y-y ij Perpendekan aksial cui menghasilkan gaya tekan aksial F = icu L AE Dimana : x dan y merupakan komponen dari ; pi = - pj = Fc qi = - qj = Fs Komponen ini menghasilkan kesetimbangan statis, sehingga diperoleh : L AE
- 45. K = C2 CS -C2 -CS CS S2 -CS -S2 -C2 -CS C2 CS -CS -S2 CS S2 Hasil yang sama juga akan diperoleh dengan cara memberikan perpindahan pada vi, uj, dan vj, dimana gaya bekerja sendiri-sendiri. Dan jika 4 dof dengan nilai tidak nol bekerja bersama-sama, dan dengan superposisi masing-masing elemen matriks kekakuan, dapat dihitung sebagai berikut : L AE
- 46. C2 CS -C2 -CS CS S2 -CS -S2 -C2 -CS C2 CS -CS -S2 CS S2 ui vi uj vj pi qi pj qj K = 1 0 -1 0 0 0 0 0 -1 0 1 0 0 0 0 0 Hubungan matriks kekakuan dengan gaya dapat ditulis sebagai berikut : [ K ] { D } = { F } = Untuk kasus khusus : 1. Jika nilai β = 0, sebagai batang horizontal, matriks kekakuan elemen [ K ] 4 x 4 Hanya berisi 4 komponen yang tidak bernilai nol, yaitu : k11 = k33 = -k13 = -k31 = L AE L AE L AE
- 47. K = 0 0 0 0 0 1 0 -1 0 0 0 0 0 -1 0 1 1. Jika nilai β = 90, sebagai batang vertikal, matriks kekakuan elemen [ K ] 4 x 4 Hanya berisi 4 komponen yang tidak bernilai nol, yaitu : k22 = k44 = -k24 = -k42 = L AE L AE
- 48. Sebuah Konstruksi Rangka Batang dengan luas A dan Modulus Elastisitas E yang sama, seperti pada Gambar L L L L 1 4 3 765 2 3 4 2 5 1 v u Hitunglah matriks kekakuaan masing-masing elemen
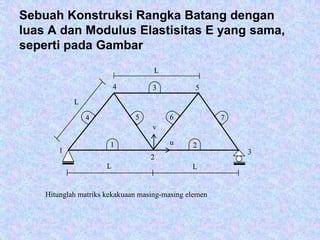
- 49. K = C2 CS -C2 -CS CS S2 -CS -S2 -C2 -CS C2 CS -CS -S2 CS S2 K1 = 1 0 -1 0 0 0 0 0 -1 0 1 0 0 0 0 0 Perumusan untuk mencari nilai matriks kekakuan elemen dengan sudut β : Batang 1, 2 dan 3 merupakan batang horizontal, sehingga β = 0o Maka : [ K1 ] = [ K2 ] = [ K3 ] L AE L AE
- 50. K4 = 0,250 0,433 -0,250 -0,433 0,433 0,750 -0,433 -0,750 -0,250 0,433 0,250 -0,433 -0,433 -0,750 0,433 0,750 K5 = 0,250 -0,433 -0,250 0,433 -0,433 0,750 0,433 -0,750 -0,250 0,433 0,250 -0,433 0,433 -0,750 - 0,433 0,750 Batang 4 dan 6 merupakan batang diagonal dengan sudut β = 60o Dimana : C = cos 60o = 0,5 S = sin 60o = 0,866 Maka : [ K4 ] = [ K6 ] Batang 5 dan 7 merupakan batang diagonal dengan sudut β = 300o Dimana : C = cos 300o = 0,5 S = sin 300o = -0,866 Maka : [ K5 ] = [ K7 ] L AE L AE