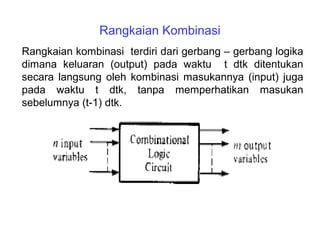
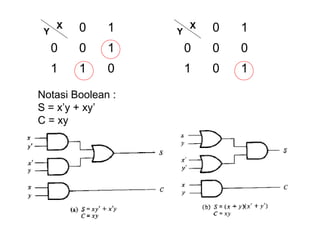
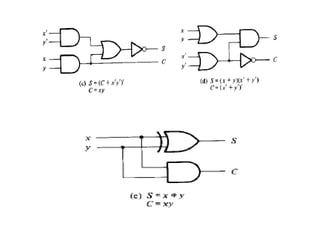
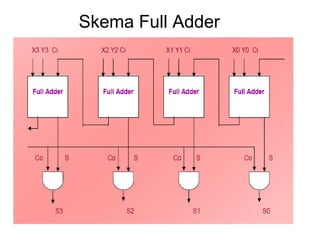
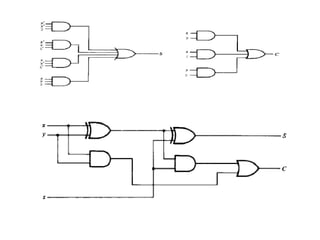
Rangkasan dokumen tersebut adalah: (1) Rangkasian kombinasi seperti adder dan subtractor digunakan untuk operasi aritmatika biner seperti penjumlahan dan pengurangan; (2) Sistem bilangan biner bertanda menggunakan representasi komplemen kedua untuk menyatakan bilangan positif dan negatif; (3) Operasi aritmatika biner melibatkan aplikasi aturan-aturan logika pada tabel kebenaran rangkaian kombinasi.

1. Aritmatika Biner
&
Rangkaian Kombinasi
(Adder, Subtractor)
By Muzakki

2. Penjumlahan
Aturan dasar penjumlahan pada sistem bilangan
biner :
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, simpan (carry) 1

3. 103
(1000)
102
(100)
101
(10)
100
(1)
8
3
2
3
3
8
Simpan (carry) 1 1
Jumlah 1 1 6 1
Penjumlahan Desimal
25
32
24
16
23
8
22
4
21
2
20
1
1
1
1
1
0
0
0
1
1
1
Simpan (carry) 1 1 1 1
Jumlah 1 1 0 1 0 0
Penjumlahan Biner

4. Kelemahan Unsigned Integer
• Hanya dapat menyatakan bilangan positif
saja
• Sistem ini tidak bisa digunakan untuk
menyatakan integer negatif

5. Bit Bertanda
Bit 0 menyatakan bilangan positif
Bit 1 menyatakan bilangan negatif
A6 A5 A4 A3 A2 A1 A0
0 1 1 0 1 0 0 = + 52
B6 B5 B4 B3 B2 B1 B0
1 1 1 0 1 0 0 = - 52
Bit Tanda
Bit Tanda
Magnitude
Magnitude

6. Kelemahan Representasi Nilai Tanda
• Adanya representasi ganda pada nilai 0
– -000000002 = - 0
– 100000002 = + 0
• Masalah pada operasi aritmatika
penjumlahan dan pengurangan yang
membutuhkan pertimbangan tanda
maupun nilai bilangan

7. Metode untuk menyatakan bit bertanda digunakan sistem
komplement kedua (2’s complement form)
Komplemen ke 2
Komplemen ke 1
Biner 0 diubah menjadi 1
Biner 1 diubah menjadi 0
1 0 1 1 0 1 0
0 1 0 0 1 0 1
Misal
Biner Awal
Komplemen pertama

8. Membuat Komplemen ke 2
1. Ubah bit awal menjadi komplemen pertama
2. Tambahkan 1 pada bit terakhir (LSB)
1 0 1 1 0 1
0 1 0 0 1 0
1
0 1 0 0 1 1
Misal
Biner Awal = 45
Komplemen 1
Tambah 1 pada LSB
Komplemen 2

9. Menyatakan Bilangan Bertanda dengan Komplemen ke 2
1. Apabila bilangannya positif, magnitude dinyatakan
dengan biner aslinya dan bit tanda (0) diletakkan di
depan MSB.
2. Apabila bilangannya negatif, magnitude dinyatakan
dalam bentuk komplemen ke 2 dan bit tanda (1)
diletakkan di depan MSB
0 1 0 1 1 0 1 Biner = + 45
1 0 1 0 0 1 1 Biner = - 45
Bit Tanda
Bit Tanda
Biner asli
Komplemen ke 2

10. Negasi
Operasi mengubah sebuah bilangan negatif menjadi
bilangan positif ekuivalennya, atau mengubah
bilangan positif menadi bilangan negatif ekuivalennya.
Hal tersebut dilakukan dengan meng-komplemenkan
ke 2 dari biner yang dikehendaki
Misal : negasi dari + 9 adalah – 9
+ 9 = 01001 Biner awal
- 9 = 10111 Negasi (Komplemen ke 2)
+ 9 = 01001 Di negasi lagi

11. Dua bilangan positif
Dilakukan secara langsung. Misal penjumlahan +9 dan +4
Penjumlahan di Sistem Komplemen ke 2
+9  0 1 0 0 1
+4  0 0 1 0 0
0 1 1 0 1
Bit tanda ikut dalam operasi penjumlahan

12. Bilangan positif dan sebuah bilangan negatif
yang lebih kecil
Misal penjumlahan +9 dan -4. Bilangan -4 diperoleh dari
komplemen ke dua dari +4
+9  0 1 0 0 1
-4  1 1 1 0 0
0 0 1 0 11
Carry diabaikan, hasilnya adalah 00101 ( = +5)

13. Bilangan positif dan sebuah bilangan negatif
yang lebih Besar
Misal penjumlahan -9 dan +4. Bilangan -9 diperoleh dari
komplemen ke dua dari +9
-9  1 0 1 1 1
+4  0 0 1 0 0
1 1 0 1 1
Bit tanda ikut dalam operasi penjumlahan

14. Dua Bilangan Negatif
Misal penjumlahan -9 dan -4. Bilangan -9 dan - 4 masing –
masing diperoleh dari komplemen ke dua dari +9 dan -4
-9  1 0 1 1 1
-4  1 1 1 0 0
1 0 0 1 1
Bit tanda ikut dalam operasi penjumlahan
1
Carry diabaikan

15. Operasi Pengurangan
Aturan Umum
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
0 – 1 =1 , pinjam 1
1 1 1 0
1 0 1 1
1 1 Pinjam
0 0 1 1 Hasil
Misal

16. Operasi Pengurangan
Operasi pengurangan melibatkan komplemen ke 2 pada
dasarnya melibatkan operasi penjumlahan tidak
berbeda dengan contoh – contoh operasi penjumlahan
sebelumnya.
Prosedur pengurangan
1. Negasikan pengurang.
2. Tambahkan pada yang dikurangi
3. Hasil penjumlahan merupakan selisih antara
pengurang dan yang dikurangi

17. Misal : +9 dikurangi +4
+9  01001
+4  00100 -
Operasi tersebut akan memberikan hasil yang sama
dengan operasi
+9  01001
-4  11100 +
+9  0 1 0 0 1
-4  1 1 1 0 0
0 0 1 0 11
Carry diabaikan, hasilnya adalah 00101 ( = +5)

18. 1 0 0 1 9
1 0 1 1 11
1 0 0 1
1 0 0 1
0 0 0 0
1 0 0 1
1 1 0 0 0 1 1 99
Perkalian Biner
Perkalian biner dilakukan sebagaimana perkalian desimal

19. Rangkaian Kombinasi
Rangkaian kombinasi terdiri dari gerbang – gerbang logika
dimana keluaran (output) pada waktu t dtk ditentukan
secara langsung oleh kombinasi masukannya (input) juga
pada waktu t dtk, tanpa memperhatikan masukan
sebelumnya (t-1) dtk.

20. Adder (penjumlah)
Half Adder
Half Adder adalah rangkaian logika yang keluarannya
merupakan jumlahan dari 2 bit. Input terdiri dari input X dan
Y, dan keluarannya berupa S (jumlahan) dan C (Carry).
Tabel Kebenarannya :
X Y C S
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

21. 0 1
0 0 1
1 1 0
X
Y 0 1
0 0 0
1 0 1
X
Y
Notasi Boolean :
S = x’y + xy’
C = xy

23. Full Adder
Rangkaian Full Adder merupakan rangkaian kombinasi
yang membentuk penjumlahan aritmatika dari 3 bit input.
Terdiri dari 3 bit input ( x, y, z) dan 2 bit output ( S dan C).
X dan Y menyatakan dua bit yang akan dijumlahkan dan z
menyatakan carry dari keadaan sebelumnya.
Tabel Kebenaran
X Y Z C S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1

24. Skema Full Adder

25. 00 01 11 10
0 1 1
1 1 1
yz
x
00 01 11 10
0 1
1 1 1 1
yz
x
S = x’y’z + x’yz’ + xy’z’ + xyz
C = xy + xz + yz

27. Pengurang (Subtractor)
Half Subtractor
Merupakan rangkaian kombinasi yang digunakan untuk
mendapatkan selisih dari dua bit input (masukkannya).
Input terdiri dari x dan y, an keluaran terdiri dari B (Borrow)
dan D (Difference).
Tabel Kebenaran X Y B D
0 0 0 0
0 1 1 1
1 0 0 1
1 1 0 0
D = x’y + xy’ B = x’y
Tampak notasi boolean untuk D mempunyai notasi yang
sama dengan notasi bolean S

28. Full Subtractor
Merupakan rangkaian kombinasi yang membentuk
pengurangan antara 2 bit dengan memperhitungkan 1
yang dipinjam dari posisi sebelumnya. Rangkaian Full
Subtractor memiliki 3 input (x,y,z) dan dua output (B dan
D).
Tabel Kebenaran dari Full Subtractor
X Y Z B D
0 0 0 0 0
0 0 1 1 1
0 1 0 1 1
0 1 1 1 0
1 0 0 0 1
1 0 1 0 0
1 1 0 0 0
1 1 1 1 1
D = x’y’z + x’yz’ +xy’z’ + xyz
B = x’y + x’z + yz

29. THANK