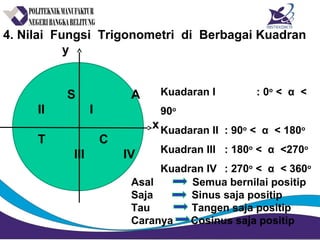
Dokumen tersebut membahas tentang trigonometri, yang meliputi pengukuran sudut, perbandingan rumus trigonometri, perbandingan trigonometri pada segitiga siku-siku, nilai fungsi trigonometri di berbagai kuadran, grafik fungsi trigonometri, kesamaan trigonometri, dan contoh soal. Secara ringkas, dokumen tersebut memberikan penjelasan mengenai dasar-dasar trigonometri beserta contoh penerapannya.

1. MATEMATIKA- IMATEMATIKA- I
Oleh:
Dr. Parulian Silalahi, M.Pd
TrigonometriTrigonometri
http://matematikapolman.esy.es

2. 1. Pengukuran Sudut
1 derajat adalah besar sudut yang disapu
oleh jari-jari lingkaran sejauh 1/360
putaran.
1 derajat = 60 menit ( 1o
= 60’) atau
1 menit = 1/60 derajat
1 derajad = π/180 radian = 0, 017 radian
1 radian = 180/ π derajat = 57, 296o

3. Contoh:
1.Sederhanakan bentuk-bentuk berikut:
a. 32o
20’ b. 15o
6”
Jawab:
a. 20’ = 20/60 o
= 0,33o
Jadi 32o
20’ = 32, 33o
b. 6” = 6/3600 = 0.0017o
Jadi 15o
6” = 15,0017o

4. 2. Nyatakan sudut berikut dalam ukuran
derajat:
a. π/3 radian
b. 2/5 radian
Jawab:
a. π/3 radian = π/3 . 180/ π derajat = 60o
b. 2/5 radian = 2/5 . 57,296o
= 22,92o

5. 2. Perbandingan rumus trigonometri
a.Sin A = 1/ cosec A
b.Cos A = 1/sec A
c.Tg A = 1/cotg A
d.TgA = sin A/ cos A
e.Cotg A = cos A/ sin A

6. 3. Perbandingan Trigonometri pada Segitiga Siku-
siku
Contoh:
Diketahui αo
sudut lancip dan sin αo
= 3/5.
Tentukan nilai perbandingan trigonometri sudut
αo
yang lain
Jawab:
b= 5
a= 3
αo
c
C =
41635 22
22
==−=
− ab

7. Jadi, nilai perbandingan trigonometri sudut αo
yang lain adalah:
Cos αo
= 4/5
Tg αo
= 3/4
Sec αo
= 5/4
Cosecαo
= 5/3
Cotg αo
= 4/3

8. Kuadaran I : 0o
< α <
90o
Kuadaran II : 90o
< α < 180o
Kuadran III : 180o
< α <270o
Kuadran IV : 270o
< α < 360o
4. Nilai Fungsi Trigonometri di Berbagai Kuadran
y
S A
II I
x
T C
III IV
Asal Semua bernilai positip
Saja Sinus saja positip
Tau Tangen saja positip
Caranya Cosinus saja positip

9. Nilai Fungsi Trigonometri

10. 5. Grafik Fungsi
Grafik y = sin x

11. Grafik Cosinus

12. Grafik Tangen

13. 6. Kesamaan Trigonometri
a.Kesamaan Genap-Ganjil
1. sin (–x) = - sin x
2. cos (-x) = cos x
3. tg (-x ) = - tg (x)
b. Kesamaan Pyhtagoras
1. sin2
t + cos2
t = 1
2. 1 + tg2
t = sec2
t
3. 1 + cot2
t = cosec2
t

14. c. Kesamaan Penambahan
1. sin (x±y) = sin x.cos y ± cos x.sin y
2. cos (x±y) = cos x.cosy sin x.sin y
3. tg (x ± y) =
d. Kesamaan Sudut Ganda
1. Sin 2x = 2 sin x.cos x
2. Cos 2 x = cos2
x - sin2
x
= 2 cos2
x - 1
= 1- 2 sin2
x
tgytgx
tgytgx
.1
±



15. e. Kesamaan Setengah Sudut
1. sin2
x =
2. cos2
x=
f. Kesamaan Hasil Kali
1. sin x. sin y = -½ [cos (x+y) – cos (x-y)]
2. cos x. cos y= ½ [cos (x+y) + cos (x-y)]
3. sin x. cos y= ½ [sin (x+y) + sin (x-y)]
4. cos x. sin y= ½ [sin (x+y) - sin (x-y)]
2
2cos1 x−
2
2cos1 x+

16. Contoh:
1.Jika tg A = 5/12, dan 0 < A < 90o
, hitunglah
a. sec A
b. cos A
Jawab:
a. 1 + tg2
A= sec2
A
1 + (5/12)2
=sec2
A
169/144= sec2
A sec A = 13/12
b. Cos A = 1/sec A = 12/13

17. 2. Jika sin P = 3/5 dan cos Q= 5/13
tentukanlah
a. sin (P + Q)
b. cos (P + Q)
c. sin 2P
Jawab:
sin2
P + cos2
P = 1
(3/5)2
+ cos2
P = 1
cos2
P = 1- 9/25 = 16/25
Cos P = 4/5
sin2
Q + cos2
Q= 1
sin2
Q+ (5/13)2
= 1
sin2
Q = 1- 25/169 =
144/169
sin Q = 12/13

18. a. Sin (P + Q) = sin P cos Q + cos P. sin Q
= 3/5 . 5/13 + 4/5 . 12/13
= 15/65 + 48/65 = 63/65
b. cos (P + Q) = cosP .cos Q – sin P. sin Q
= 4/5.5/13 - 3/5. 12/13
= 20/65- 36/65 = -16/65
c. Sin 2P = 2 sin P cos P
= 2. 3/5. 4/5 = 24/25

19. Perbandingan trigonometri sudut – sudut berelasi
Kuadran I
Kuadran II

20. Perbandingan trigonometri sudut – sudut berelasi
Kuadran III
Kuadran IV

21. TERIMA KASIH
Selamat Belajar
http://matematikapolman.esy.es/