Downloaded 13 times
Uploaded byTulus Setyawan
Perkalian matrik elementer
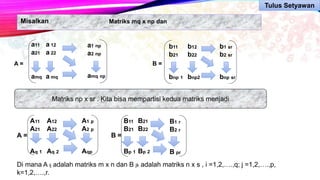
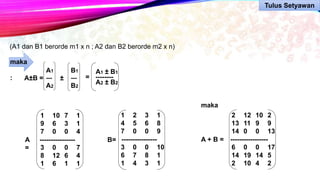
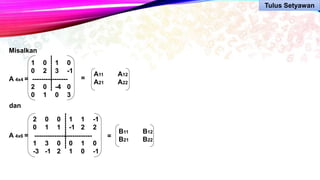
Dokumen ini membahas metode perhitungan invers matriks dan penerapannya dalam pengolahan citra digital, termasuk partisi matriks besar menjadi matriks yang lebih kecil untuk efisiensi. Terdapat penjelasan tentang operasi penjumlahan dan pengurangan matriks serta contoh perkalian matriks. Metode ini penting untuk mengatasi keterbatasan memori saat memproses citra berukuran besar.
More Related Content
![Persamaan Diferensial [orde-2]](https://cdn.slidesharecdn.com/ss_thumbnails/persamaandiferensialorde-2-150706213036-lva1-app6892-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Perkalian matrik elementer
![Modul Ajar Kurikulum Berbasis Cinta (KBC) Bahasa Arab Kelas 4 [modulguruku.com]](https://cdn.slidesharecdn.com/ss_thumbnails/modulajarkurikulumberbasiscintakbcbahasaarabkelas4modulguruku-260111161038-33bb50cf-thumbnail.jpg?width=640&height=640&fit=bounds)
![Modul Ajar Kurikulum Berbasis Cinta (KBC) Fikih Kelas 5 [modulguruku.com]](https://cdn.slidesharecdn.com/ss_thumbnails/modulajarkurikulumberbasiscintakbcfikihkelas5modulguruku-260112161659-0c632371-thumbnail.jpg?width=640&height=640&fit=bounds)
Perkalian matrik elementer
- 2. Hitung invers matrikA A = 2 3 4 3 4 5 4 5 5 Jawab : Menghitung E1 A1 = 2 3 4 ; A2 = 3 4 5 ;A3 = 4 5 5 E1 = 1/a11 0 0 −a21/a11 1 0 −a31/a11 0 1 = 0.5 0 0 −1.5 1 0 −2 0 1 Menghitung E2 N2 = E1A2 = 0.5 0 0 −1.5 1 0 −2 0 1 3 4 5 = 1.5 −0.5 −1 E2 = 1 −1.5/−0.5 0 0 1/−0.5 0 0 −(−1)/(−0.5) 1 = 1 3 0 0 −2 0 0 −2 1 E2E1 = 1 3 0 0 −2 0 0 −2 1 0.5 0 0 −1.5 1 0 2 0 1 = −4 3 0 3 −2 0 1 −2 1 Tulus Setyawan
- 3. 1. Matrikelementeradalahmatrik yang diperolehdarioperasielementeryang dikenakanpadamatrikidentitas. 2. Setiapmatrikelementermempunyai invers, dansetiapmatrikbujursangkarberordo (nxn) yang mempunyai invers ekivalenbaristerhadapmatrikidentitas I. 3. Akibatnyajika : EkEk-1Ek-2…E2E1A = I, maka, A-1 = EkEk-1Ek-2…E2E1 Matrikelementer E diperolehdaritransformasimatrikidentitasdiman apadakolomke-I digantidengannormalitas vector kolom : Ei = 1 0 … 0 1 … … 0 … 0 … 0 … 0 … … … 𝑁 𝑘. 𝑖 𝑁 𝑘. 𝑖 ⋯ 𝑁 𝑘. 𝑖 … … … … 0 0 ⋯ 0 … … 𝑁 𝑘. 𝑖 … 0 Nk,I = a1, 𝑖/a𝑖𝑖 … 1/a𝑖𝑖 … −a 𝑛, 𝑖/a𝑖𝑖 dimana: Nk,I = Ei-1Ei-2…E1IAi Tulus Setyawan
- 4. Menghitung E3 danInvers Matrik N3 = E2E1A3 = −4 3 0 3 −2 0 1 −2 1 4 5 5 = −1 2 −1 E3 = 1 0 −(−1)/(−1) 0 1 −(2)/(−1) 0 0 1/(−1) = 1 0 −1 0 1 2 0 0 −1 Jadi Invers Matriknya A-1 = E3E2E1 = 1 0 −1 0 1 2 0 0 −1 −4 3 0 3 −2 0 1 −2 1 = −5 5 −1 5 −6 2 −1 2 −1 Tulus Setyawan
- 5. Dalam teori pengolahancitra digital, sebuah citra direpresentasikan sebagai matriks yang ukurannya sangat besar. Mengolah citra digital, berarti mengolah matriks tersebut. Untuk mempermudah perhitungan terkadang sebuah matriks yang besar perlu dipartisi (disekat) terlebih dahulu. Partisi dilakukan dengan cara membagi matriks yang besar menjadi sub-sub matriks yang lebih kecil. Sebagai contoh, diketahui dua buah citra berukuran 10000 X 10000 piksel yang dinyatakan sebagai matriks berukuran 10000 X 10000 berikut : Tulus Setyawan
- 6. a 11 a 21 a10000 1 a 12 a 22 a 10000 1 a 1 10000 a 2 10000 a 10000 10000 A= b 11 b 21 b 10000 1 b 12 b 22 b 10000 1 b 1 10000 b 2 10000 b 10000 10000 B= Untuk memproses kedua citra tersebut dibutuhkan waktu sangat lama dan seringkali tidak mungkin untuk mengalikan kedua matriks karena terbatasnya memori computer untuk menyimpan kedua matriks tersebut. Tulus Setyawan
- 7. A11 A21 A100 1 A12 A22 A100 2 A1100 A2 100 A100 100 B = B11 B21 B100 1 B12 B22 B100 2 B1 100 B2 100 B100 B100 Untuk meyelesaikan permasalahan ini kedua matriks tersebut dipecah-pecah (dipartisi) menjadi matriks yang berukuran lebih kecil, misalnya menjadi matriks berukuran 100 X100. Dimana Aij, Bij, i=1,2,…,100, adalah matriks ordo 100 X 100 . Bila dilakukan operasi perkalian matriks, maka Tulus Setyawan
- 8. A11 A21 A100 1 A12 A22 A100 2 A1 100 A2100 A100 100 B11 B21 B100 1 B12 B22 B100 2 B1 100 B2 100 B100 100 = C11 C21 C100 1 C12 C22 C100 2 C1 100 C2 100 C100 100 = C Dimana Cij = ∑ Aik Bkj = Ai1 B1j + Ai2 B2j + …. + Ai100 B100j, i = 1,2,…,100; j = 1,2,….,100. Sebagai contoh, C12 = ∑ A1k BK2 = A11B12+A12B22+….+A1 100B100 2 Jadi, kita hanya perlu untuk menghitung perkalian matriks 100 X 100 . Kasus Umum 100 K=1 100 K=1
- 9. a11 a21 amq a 12 a 22 amq a1 np a2 np amq np B = b11 b21 bnp 1 b12 b22 bnp2 b1 sr b2 sr bnp sr A = Misalkan Matriks mq x np dan Matriks np x sr . Kita bisa mempartisi kedua matriks menjadi A11 A21 Aq 1 A = A12 A22 Aq 2 A1 p A2 p Aqp B = B11 B21 Bp 1 B21 B22 Bp 2 B1 r B2 r B pr Di mana A ij adalah matriks m x n dan B jk adalah matriks n x s , i =1,2,….,q; j =1,2,….,p, k=1,2,….,r. Tulus Setyawan
- 10. Matriks A4x4 disekatdengan satu dipartisi horizontal menjadi A1;2x4 dan A2;2x4. A= A1 --- A2 = 1 2 3 4 5 6 7 8 ---------------- 8 7 6 5 4 3 2 1 AT = A1 A2 --- = 1 5 8 4 2 6 7 3 3 7 6 2 4 8 5 1 ------------ Jika sebuah matriks berorde m x n dipartisi dengan satu sekatan vertical, maka akan diperoleh dua buah matriks berorde m x n1 dan m x n2, dimana n1+n2=n Matriks B3x4 dipartisi dengan satu partisi vertical menjadi B1; 3x2 dan B2; 3x2. Tulus Setyawan
- 11. Biasanya partisi yangdilakukan adalah sekali secara horizontal dan sekali secara vertical. B= B1 B2 = 1 2 3 4 8 7 6 5 9 2 3 7 --- --------- B = T B B T T 1 2 --- = 1 8 9 2 7 2 3 6 3 4 5 7 ------------ C= C11 C1 2 C21 C2 2 -------- -------- = 1 2 3 4 5 6 7 8 9 3 2 1 --------------- ------------ C = T T T C C C C T T 11 12 21 22 ----------- ----------- = 1 4 7 3 2 5 8 2 3 6 9 1 ----------------- ------------ Tulus Setyawan
- 12. C11 berorde m1x n1 C12 berorde m1 x n2 C21 berorde m2 x n2 C22 berorde m2 x n2 (perhatikan perpindahan sekat antara C12 dan C21!) OPERASI PENJUMLAHAN DAN PENGURANGAN • Partisi Vertikal A mxn = A1 A2 --- B mxn = B1 B2 --- (A1 dan B1 berorde mxn1; A2 dan B2 berorde mxn2) maka: A±B = A1 A2 --- ± B1 B2 --- = A1 ± B1 A2 ± B2 Tulus Setyawan
- 13. A = 2 71 1 9 2 4 5 0 8 4 8 7 6 1 0 2 5 8 2 3 5 3 6 2 1 1 1 12 2 --------------- B= 2 8 1 1 9 2 3 6 6 6 3 4 4 1 7 7 2 5 5 2 3 5 3 5 2 1 1 1 7 2 --------------- A – B = 0 -1 0 0 0 0 1 -1 -6 2 1 4 3 5 -6 -7 0 0 3 0 0 0 0 1 0 0 0 0 5 0 --------------- Partisi Horizontal A mxn = A1 --- A2 B mxn = B1 --- B2 Tulus Setyawan
- 14. (A1 dan B1berorde m1 x n ; A2 dan B2 berorde m2 x n) A1 ± B1 A±B = A1 --- A2 ± B1 --- B2 = A2 ± B2 -------- A = 1 10 7 1 9 6 3 1 7 0 0 4 3 0 0 7 8 12 6 4 1 6 1 1 ---------------- B= 1 2 3 1 4 5 6 8 7 0 0 9 3 0 0 10 6 7 8 1 1 4 3 1 ---------------- maka : maka A + B = 2 12 10 2 13 11 9 9 14 0 0 13 6 0 0 17 14 19 14 5 2 10 4 2 ----------------- Tulus Setyawan
- 15. OPERASI PERKALIAN 0perasi perkalianterhadap dua matriks A dan B adalah sebagai berikut: AB = A11 A21 Aq 1 A12 A22 Aq 2 A1 p A2 p Aqp B11 B21 Bp 1 B21 B22 Bp 2 B1 r B2 r B pr = C11 C21 Cq 1 C21 C22 Cq 2 C1 r C2 r C qr = C mqxsr dimana Cij = ∑ Aij Bkj = Ai 1 B1 j + Ai 2 B2 j + …. + Aip Bpj , i =1,2,…,q; j =1,2,…,r, adalah matriks mxs K=1 p Tulus Setyawan
- 16. Misalkan A 4x4 = 10 1 0 0 2 3 -1 2 0 -4 0 0 1 0 3 ---------------- ---------------- = A11 A12 A21 A22 dan A 4x6 = 2 0 0 1 1 -1 0 1 1 -1 2 2 1 3 0 0 1 0 -3 -1 2 1 0 -1 -------------------------- ---------------- = B11 B12 B21 B22 Tulus Setyawan
- 17. dimana A11 1 0 02 = , A12 = 1 0 3 -1 , A21 = 2 0 0 1 , A22 = -4 0 0 3 dan B11 = 1 0 0 0 2 1 , B12 = 1 1 -1 -1 2 2 , B21 = 1 3 0 -3 -1 2 , B22 = 0 1 0 1 0 -1 Maka perkalian matriks A dan B adalah A 4x4B 4x6 = A11 A12 A21 A22 B11 B12 B21 B22 = A11B11+A12B21 A11B12+A12B22 A21B11+A22B21 A21B12+A22B22 =C 4x6 = C11 C12 C21 C22 = 3 3 0 1 2 -1 6 12 0 -3 7 5 0 -12 0 2 -2 -2 -9 -2 7 2 2 -1 -------------------------- ---------------- Tulus Setyawan
- 18. Contoh 1 A = 12 5 3 4 7 3 4 8 1 2 6 2 3 6 1 5 8 --------- A1 A2 --- = B = B1 --- B2 = 1 3 3 5 5 2 7 6 2 4 4 3 ------ A1B1= 1 2 5 3 4 8 2 3 6 1 3 3 5 5 2 = 1.1+2.3+5.5 1.3+2.5+5.2 3.1+4.3+8.5 3.3+4.5+8.2 2.1+3.3+6.5 2.3+3.5+6.2 = 32 23 55 45 41 33 A2B2 3 4 7 1 2 6 1 5 8 7 6 2 4 4 3 = 3.7+4.2+7.4 3.6+4.4+7.3 1.7+2.2+6.4 1.6+2.4+6.3 1.7+5.2+8.4 1.6+5.4+8.3 = 57 55 35 32 49 50 AB = = A1B1 + A2B2 = 89 78 90 77 90 83 Tulus Setyawan
- 19. Contoh 2 A = 31 2 5 6 4 8 3 9 5 7 2 ---------------- ------------- B = 5 3 1 2 4 6 7 2 4 1 5 8 2 5 8 3 4 7 4 3 1 6 7 12 -------------------------- ---------------- A11B11 + A12B21= 3 1 6 4 5 3 1 7 2 4 + 2 5 8 3 2 5 8 4 3 1 = 22 11 7 58 26 22 + 24 25 21 28 49 67 = 46 36 28 86 75 89 A11B12 + A12B22= 3 1 6 4 2 4 6 1 5 8 + 2 5 8 3 3 4 7 6 7 12 Tulus Setyawan
- 20. 7 17 26 1644 68 = + 36 43 74 42 53 92 = 43 60 100 58 97 160 A21B11+A22B21= 9 5 2 4 6 1 5 8 + 7 2 = 80 37 29 + 22 41 58 = 10278 87 A21B12+A22B22= 9 5 + 7 2 3 4 7 6 7 12 5 3 1 7 2 4 2 5 8 4 3 1 = 23 61 94 + 33 42 73 = 56 103167 Tulus Setyawan
- 21. AB = A11B11+A12B21 A11B12+A12B22 A21B11+A22B21A21B12+A22B22 ---------------------------------------- --------- AB = 46 36 28 43 60 100 86 75 89 58 97 160 10278 87 56 103167 ----------------------------- ------------- Contoh 3 Toyes adalah dokter ahli penyakit cinta di Indonesia. Ia mempunyai pasien seorang wanita warga Virgnia bernama Sylvi yang mengeluhkan bahwa selama 10 tahun ini hatinya sakit karena ditinggal pacarnya. Untuk mengetahui adanya penyakit – penyakit lain yang ditimbulkan oleh sakit hati tersebut, Toyes memutuskan pergi ke Virginia untuk melakukan CT Scan pada kepala Sylvi dan mengambil citra iris matanya untuk mengetahui kemungkinan adanya penyakit yang lain. Tulus Setyawan
- 22. Dari proses fotoCT Scan dan pengambilan citra iris mata dihasilkan citra berukuran 20 M dan 15 M. Kedua citra tersebut akan dikirim ke Indonesia segera, untuk kebutuhan analisis dan hasilnya harus dikirim ke Virginia dalam waktu 2 hari. Bagaimana cara mengirim data sebesar ini, agar tidak putus di tengah jalan dan cepat sampai di tempat tujuan? JAWAB Pengiriman data yang terlalu besar mengakibatkan data mudah putus di tengah jalan, kalaupun tidak sampai putus, data tiba di tempat dalam waktu yang sangat lama. Untuk mengatasi hal ini data citra disimpan dalam bentuk matriks, kemudian dilakukan partisi menjadi data – data kecil misalnya berukuran 1 M. Tulus Setyawan
- 23. Data kecil inidikirim secara bertahap hingga lengkap. Sampai di tempat, data ini digabung lagi menjadi matriks yang besar, dan menghasilkan citra semula yang berukuran 20 M dan 15 M. Partisi matrik A yang berordo (mxn) adalah sub matrik-sub matrik yang diperoleh dari A dengan cara memberikan batasan-batasan garis horisontal diantara dua baris dan atau memberikan batasan-batasan garis vertikal diantara dua kolom. Tulus Setyawan
- 24. CONTOH 6863 4753 5532 4321 A 68 47 A 63 53 A 55 43 A 32 21 A :adalahAmatrikPartisi 2221 1211 Andaikan A matrikbujur sangkar berordo (nxn) yang mempunyai invers, yaitu : A–1 = B, dan partisinya masing- masing adalah : Karena, AB=BA=I maka diperoleh : 2221 1211 2221 1211 BB BB B; AA AA A I0 0I AA AA BB BB I0 0I BB BB AA AA 2221 1211 2221 1211 2221 1211 2221 1211 Tulus Setyawan
- 25. Dari perkalian matrikdiperoleh hasil : (1). A11 B11 + A12 B21 = I (2). A11 B12 + A12 B22 = 0 (3). B21 A11 + B22 A21 = 0 (4). B21 A12 + B22 A22 = I Dengan asumsi, A11 –1 ada, dan B22 = L–1 ada Maka rumus untuk menghitung inver matriknya adalah : (1). B12 = –(A 11 –1 A12)L–1 (2). B21 = – L–1(A21 A11 –1) (3). B11 = A11 –1+(A11 –1A12)L–1(A21 A11 – 1) (4). L = A22 – (A21A11 –1A12) CONTOH : Kasus n=4. Hitunglah invers matrik berikut ini Jawab : 6863 4753 5532 4321 A 68 47 A 63 53 A 55 43 A 32 21 A :adalahAmatrikPartisi 2221 1211 Tulus Setyawan
- 26. Menghitung L 1-1 56- 1-(-1)- (-5)-6- 5-6 1 LJadi, 6-1- 5-1- 129 98 - 68 47 31 2-1 63 53 - 68 47 AAAAL 03 11 1-2 23- 63 53 AA 31 2-1 55 43 1-2 23- AA 1-2 23- 12- 2-3 )43( 1 A 1- 12 1- 112122 1- 1121 12 1- 11 1- 11 Menghitung InversMatrik 4-5 6-13 3-3 8-13 1-2 23- 12- 6-9 31 2-1 1-2 23- )A(AL)AA(AB 1-2 69- 03 11 1-1 56- - )A(A-LB 2-3 7-8 1-1 56- 31 2-1 - L)A-(AB 1- 1121 1- 12 1- 11 1- 1111 1- 1121 1- 21 1- 12 1- 1112 Tulus Setyawan
- 27. 1-112 56-69- 2-34-5 7-86-10 BB BB A 2221 12111- CONTOH : Hitung inversmatrik A berikut : Jawab : Partisi matrik A 31554 13343 53632 23443 34532 A 315 133 536 A 54 43 32 A 234 345 A 43 32 A 2221 1211 Tulus Setyawan
- 28.
- 29.
- 30.