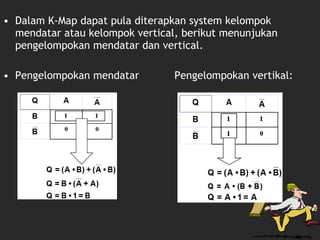
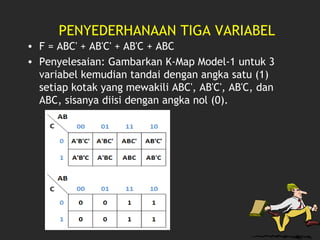
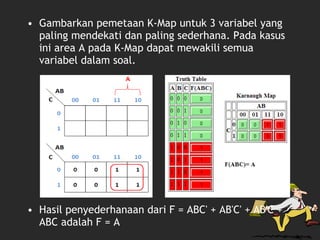
Dokumen tersebut membahas tentang Karnaugh Map dan penggunaannya untuk menyederhanakan fungsi logika. Karnaugh Map adalah pemetaan yang menggunakan kotak-kotak untuk mewakili kombinasi variabel input dan digunakan untuk menyederhanakan fungsi logika menjadi bentuk produk sumbu atau sum of products."

1. Karnaugh Map
dan
Penyederhaan dengan Karnaugh
Map
Disusun oleh:
1.Luluk Mar’ah S. K2312038
2.Alifia Dian Septi A. K2314002
3.Ary Setyaningsih K2314007
4.Cheria Drifi Asyifa K2314009
5.Egy Adhitama K2314014
6.Selfi Septiani K2314044

2. KARNAUGH MAP

3. KARNAUGH MAP
• Salah satu teknik yang paling mudah untuk
penyederhanaan rangkaian logika adalah dengan
menggunakan peta karnaugh.
• Karnaugh map adalah suatu pemetaan dengan
sejumlah kotak yang tergantung variabelnya.
• Peta karnaugh dapat digunakan untuk
menyusun :
• Aljabar Boolean Minterm
• Aljabar Boolean Maksterm

4. Penyederhanaan Fungsi Logika
• Ada dua penyederhanaan:
1. Sistem SOP (Sum Of Product)
2. Sistem POS (Product Of Sum)
• SOP ini nama lainnya persamaan
minterm dimana untuk sistem
SOP/Minterm digunakan output '1‘
• POS / Maxterm menggunakan
output '0'.

5. • Persamaan minterm di bawah adalah :
Y = A'.B'.C' + A'.B.C' + A'B.C + A.B'.C' + A.B.C
Contoh SOP / Minterm dibawah ini :

6. Contoh maxterm /POS
• Persamaan maxtermnya : Y= (A+B+C').(A'+B+C').
(A'+B'+C)

7. Langkah- langkah pemetaan menggunakan
Aljabar Boolean Minterm ( Sum Of Product
(SOP) / Jumlah Dari Perkalian
1. Menyusun Aljabar Boolean Minterm (SOP) dari
tabel kebenaran.
2. Menggambarkan satuan dalam peta karnaugh.
3. Melingkari kelompok 8, 4 atau 2 satuan
berdekatan satu sama lain.
4. Menghilangkan variabel, bila suatu variabel dan
komplemennya terdapat dalam satu lingkaran
maka variabel tersebut dapat dihilangkan.
5. Meng-OR- kan varibel yang tersisa untuk
membentuk pernyataan Aljabar Boolean
Minterm.

8. Langkah- langkah Pemetaan Menggunakan
Aljabar Boolean Maksterm (POS) :
1. Menyusun Aljabar Boolean Maksterm (POS) dari
tabel kebenaran.
2. Langkah 2, 3 dan 4 sama dengan aljabar boolean
Minterm.
5. Meng-AND- kan varibel yang tersisa untuk
membentuk pernyataan Aljabar Boolean Maksterm.

9. Analisa Masalah Untuk Membuat
Suatu Rancangan Logika
• Ubahlah fungsi tersebut menjadi bentuk SOP
(Sum of Product), sehingga menjadi :
F = AB + BC + D
• Double-bar fungsi tersebut menjadi :
F = AB + BC + D
• operasikan bar yang terbawah dari double
bar, sehingga menjadi:
F = AB * BC * D

10. Penyederhanaan fungsi logika dengan K-
Map
• Salah satu metode penyederhanaan fungsi logika untuk
maksimal 4 variabel dapat dilakukan dengan metode K-
Map (Karnaugh Map). Sebab jika lebih dari 4 variabel kita
menggunakan metode Quine Mc Cluskey.
• Map Karnaugh menggambarkan sejumlah kotak berbentukMap Karnaugh menggambarkan sejumlah kotak berbentuk
bujursangkar yang berisi MINTERM atau minimum Termbujursangkar yang berisi MINTERM atau minimum Term
dari persamaan Logika.dari persamaan Logika.
• Banyaknya kotak tergantung dari jumlah input yangBanyaknya kotak tergantung dari jumlah input yang
diberikan rangkaian logika.diberikan rangkaian logika.
Rumusan : A = 2Rumusan : A = 2nn
• DimanaDimana
• A = Jumlah KotakA = Jumlah Kotak
• n = banyaknya variabel inputn = banyaknya variabel input

11. MAP KARNAUGHMAP KARNAUGH
Variabel Input Kombinasi Jumlah Kotak
1 21
2
2 22
4
3 23
8
4 24
16

12. Penggunaan Map KarnaughPenggunaan Map Karnaugh
• Berdasarkan kepada letaknya angka logika “1”, makaBerdasarkan kepada letaknya angka logika “1”, maka
akan didapat beberapa kemungkinan yaitu :akan didapat beberapa kemungkinan yaitu :
• PairPair
merupakan satu pasang angka 1 yang berdekatan baikmerupakan satu pasang angka 1 yang berdekatan baik
secara horisontal maupun vertikal.secara horisontal maupun vertikal.
• Kuad :Kuad :
merupakan kelompok yg terdiri dari 4 buah angka 1 ygmerupakan kelompok yg terdiri dari 4 buah angka 1 yg
tersusun berdampingan dari ujung ke ujung.tersusun berdampingan dari ujung ke ujung.
• OktetOktet
merupakan kelompok dari delapan angka 1 yangmerupakan kelompok dari delapan angka 1 yang
berdampingan.berdampingan.

13. Map Karnaugh 2 variabel InputMap Karnaugh 2 variabel Input
A
B
A
0
A
1
B 0 00 10
B 1 01 11

14. Koordinat antara A dan B merupakan konjungsi, biasanya
bernilai 0 atau 1, untuk menuliskan aljabar boole diambil
kotak bernilai 1 saja:

15. Berikut terdapat 3 kotak bernilai 1:

16. • Dalam K-Map dapat pula diterapkan system kelompok
mendatar atau kelompok vertical, berikut menunjukan
pengelompokan mendatar dan vertical.
• Pengelompokan mendatar Pengelompokan vertikal:

17. Pengelompokan kombinasi:

18. PENYEDERHANAAN DUA VARIABEL
• F = AB + A'B + AB'
Penyelesaian:
• Gambarkan K-Map Model-1 untuk dua variabel Ganti
kotak-kotak yang sesuai untuk AB, A'B, dan AB,
dengan angka satu (1) dan sisanya dengan angka nol
(0)

19. • Gabungkan semua angka satu (1) sesederhana
mungkin. Untuk mempermudah dapat menggunakan
pemetaan K-Map dua variabel.
• Hasil penyederhanaan dari F = AB + A'B + AB' adalah
F = A + B
• Perbandingan dengan cara Aljabar:
F = AB + A'B + AB'
= A (B+B') + A'B
= A (1) + A'B = A + A'B = A + B

20. PENYEDERHANAAN TIGA VARIABEL
• F = ABC' + AB'C' + AB'C + ABC
• Penyelesaian: Gambarkan K-Map Model-1 untuk 3
variabel kemudian tandai dengan angka satu (1)
setiap kotak yang mewakili ABC', AB'C', AB'C, dan
ABC, sisanya diisi dengan angka nol (0).

21. • Gambarkan pemetaan K-Map untuk 3 variabel yang
paling mendekati dan paling sederhana. Pada kasus
ini area A pada K-Map dapat mewakili semua
variabel dalam soal.
• Hasil penyederhanaan dari F = ABC' + AB'C' + AB'C +
ABC adalah F = A

22. • Perbandingan dengan Aljabar:
F = ABC' + AB'C' + AB'C + ABC
= AB (C'+C) + AB' (C'+C)
= AB (1) + AB' (1)
= AB + AB'
= A (B+B')
= A (1)
= A

23. F = A'B'C + A'BC + AB'C + ABC + ABC'
• Penyelsesaian Gambarkan K-Map Model-1 untuk 3
variabel kemudian tandai dengan angka satu (1)
setiap kotak yang mewakili A'B'C, A'BC, AB'C, dan
ABC, dan ABC', sisanya diisi dengan angka nol (0).
•

24. • Gambarkan pemetaan K-Map untuk 3 variabel yang
paling mendekati dan paling sederhana. Pada kasus
ini area AB dan area C pada K-Map dapat mewakili
semua variabel dalam soal.
• Penyederhanaan dari
F = A'B'C + A'BC + AB'C + ABC + ABC' adalah
F = AB + C

25. PENYEDERHANAAN EMPAT VARIABEL
• F = A'BC'D + ABC'D + A'BCD + ABCD
• Penyelsesaian Gambarkan K-Map Model-1 untuk 4
variabel kemudian tandai dengan angka satu (1)
setiap kotak yang mewakili A'BC'D, ABC'D, A'BCD,
ABCD, sisanya diisi dengan angka nol (0).
•

26. • Gambarkan pemetaan K-Map untuk 4 variabel yang paling
mendekati dan paling sederhana. Pada kasus ini area B dab
D pada K-Map dapat mewakili semua variabel dalam soal.
• Hasil penyederhanaan dari
F = A'BC'D + ABC'D + A'BCD + ABCD adalah F = BD

27. • Perbandingan dengan Aljabar:
• F = A'BC'D + ABC'D + A'BCD + ABCD
= (A'+A) BC'D + (A'+A) BCD
= (1) BC'D + (1) BCD
= BC'D + BCD
= BD (C'+C)
= BD (1)
= BD

29. TERIMAKASIH