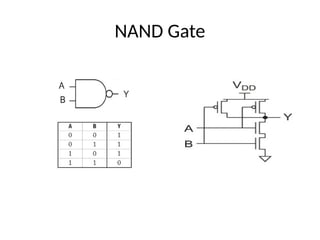
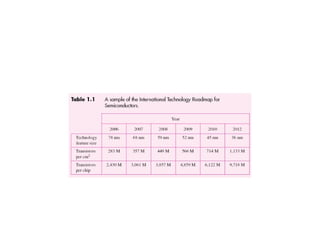
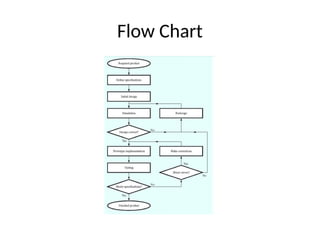
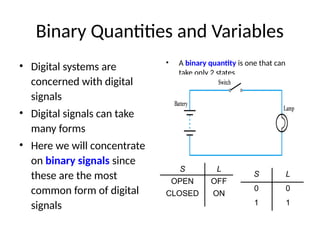
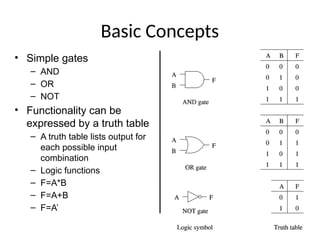
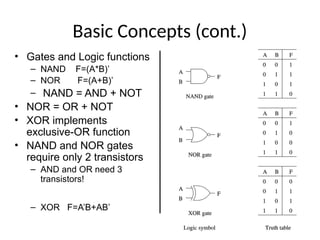
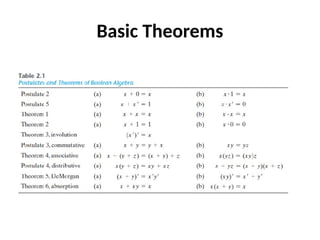
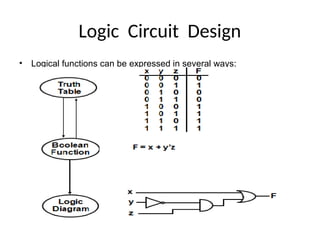
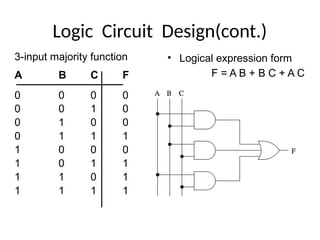
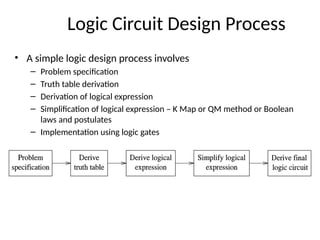
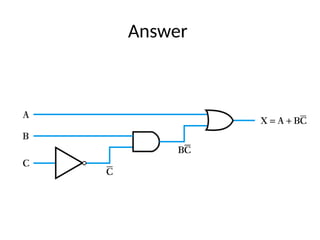
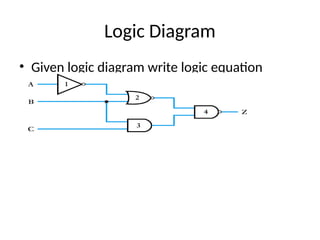
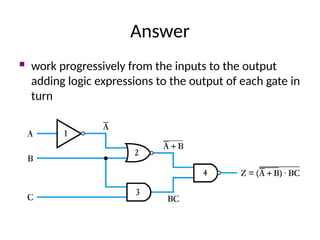
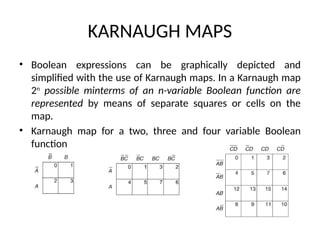
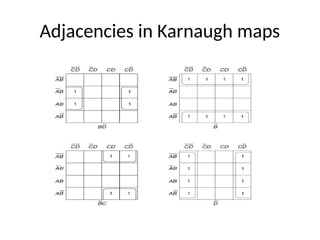
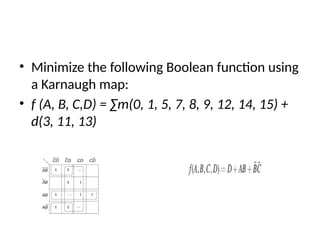
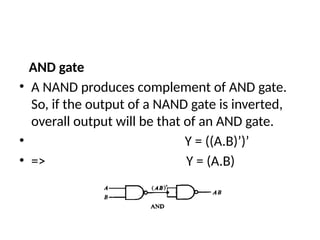
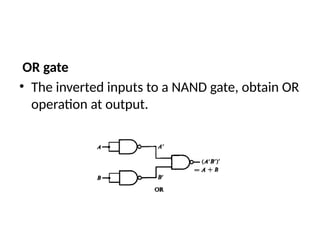
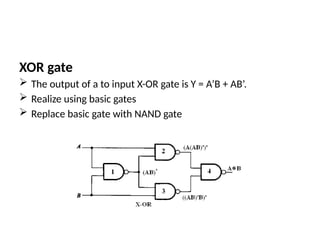
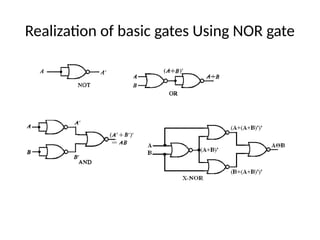
This document outlines the syllabus for a digital electronics course, covering design concepts, logic circuits, boolean algebra, and digital hardware components. It details course outcomes, including the ability to design combinational and sequential circuits, as well as write VHDL code. Additional sections discuss the design process, basic logic gates, and the application of Karnaugh maps for circuit simplification.

1. DIGITAL ELECTRONICS
BE IT III Semester
Dr. M Mohammed Sabir Hussain
Sabir.mj@gmail.com
9849217818

2. Syllabus
UNIT – I
• Design Concepts: Digital Hardware, Design
process, Design of digital hardware.
Introduction to logic circuits – Variables and
functions, Logic gates and networks. Boolean
algebra, Synthesis using gates, Design
examples. Optimized implementation of logic
functions using K-Map

3. Course Outcomes
• At the end of this course the students will be able to
• Understand the deign process of digital hardware, use Boolean algebra to
minimize the logical expressions and optimize the implementation of
logical functions.
• Understand the number representation and design combinational circuits
like adders, MUX etc.
• Design Combinational circuits using PLDS and write VHDL code for basic
gates and combinational circuits.
• Analyze sequential circuits using flip-flops and design registers, counters.
• Represent a sequential circuit using Finite State machine and apply state
minimization techniques to design a FSM

4. Suggested Readings
• 1. Moris Mano and Michael D CIletti, Digital Design,
Pearson, fourth edition,2008
• 2. Zvi Kohavi, Switching and Finite Automata Theory, 3rd
ed., Cambridge University Press-New Delhi, 2011.
• 3. R. P Jain, Modern Digital Electronics,4th ed., McGraw Hill
Education (India) Private Limited, 2003
• 4. Ronald J.Tocci, Neal S. Widmer &Gregory L.Moss, “Digital
Systems: Principles and Applications,” PHI, 10/e, 2009.
• 5. Samir Palnitkar, “Verilog HDL A Guide to Digital Design
and Synthesis,” 2nd Edition, Pearson

5. • Digital System uses
digital hardware.
• Digital computer – CPU
– Chip-IC-Gates

6. NAND Gate

7. Design Concepts
• Digital Hardware
• Design process
• Design of digital hardware

8. • Digital design is concerned with the design of
digital electronics circuits.
• Digital circuits are employed design and
construction of system such as digital
computer, data communication, digital
recording and many other applications that
require digital hardware.

9. Digital Hardware Components

15. The Design Process
Steps of a general product development process:
• 1) Define specification
• 2) Initial Design
• 3) Simulation
• 4) If Design is not correct Redesign and go to step 3
• 5) Prototype implementation
• 6) Testing
• 7) Is spec not met If minor errors Make corrections and go
to step 5 Else redesign and go to step 3
• 8) finish

16. Flow Chart

17. Design of a Digital Hardware

18. Logic Circuits
• Introduction: Logic circuits built with logic gates
• Logic gates are electronic circuits that operate
on one or more input signals to produce an
output signal.
• Electrical signals such as voltages or currents
exist as analog signals having values over a given
continuous range, say, 0 to 3 V.
• In a digital system these voltages are interpreted
to be either of two recognizable values, 0 or 1.

19. Binary Quantities and Variables
• Digital systems are
concerned with digital
signals
• Digital signals can take
many forms
• Here we will concentrate
on binary signals since
these are the most
common form of digital
signals
• A binary quantity is one that can
take only 2 states
S L
OPEN OFF
CLOSED ON
S L
0 0
1 1

20. Basic Concepts
• Simple gates
– AND
– OR
– NOT
• Functionality can be
expressed by a truth table
– A truth table lists output for
each possible input
combination
– Logic functions
– F=A*B
– F=A+B
– F=A’

21. Basic Concepts (cont.)
• Gates and Logic functions
– NAND F=(A*B)’
– NOR F=(A+B)’
– NAND = AND + NOT
• NOR = OR + NOT
• XOR implements
exclusive-OR function
• NAND and NOR gates
require only 2 transistors
– AND and OR need 3
transistors!
– XOR F=A’B+AB’

22. Logic Chips 74XX (cont.)

23. Boolean Algebra
• In 1854, George Boole developed an algebraic
system now called Boolean algebra.
• In 1938, Claude E. Shannon introduced a two valued
‐
Boolean algebra called switching algebra that
represented the properties of bistable electrical
switching circuits.
• Boolean algebra use to optimize simple circuits and
to understand the purpose of algorithms used by
software tools to optimize complex circuits involving
millions of logic gates. ( to reduce cost of the circuit)

24. Basic Definition
• Boolean algebra may be defined with a
set of elements, a set of operators, and a number of
unproved axioms or postulates.
• A set of elements is any collection of objects, usually
having a common property. If S is a set,
and x and y are certain objects, then the notation
means that x is a member of the set S
• S means that y is not an element of S.

25. • Binary operator: A binary operator defined on
a set S of elements is a rule that assigns, to
each pair of elements from S, a unique
element from S.
• Example: Consider the relation a *b = c.
We say that * is a binary operator if it specifies
a rule for finding c from the pair (a, b)

26. • Postulates: The postulates of a mathematical
system form the basic assumptions.
• Used to deduce the rules, theorems, and
properties of the system.
• The most common postulates used to
formulate various algebraic structures are as
follows:

27. • Associative law : A binary operator * on a set S is
said to be associative whenever
• Commutative law. A binary operator * on a set S is
said to be commutative whenever
• Distributive law. If * and # are two binary
operators on a set S, * is said to be distributive
over # whenever

28. • Identity element: a+0 =a , a.1 = a
• Complement : a+a’ = 1 , aa’ =0

29. Basic Theorems

30. Proofs

33. Logic Circuit Design
• Logical functions can be expressed in several ways:

34. Logic Circuit Design(cont.)
3-input majority function
A B C F
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
• Logical expression form
F = A B + B C + A C

35. Logic Circuit Design Process
• A simple logic design process involves
– Problem specification
– Truth table derivation
– Derivation of logical expression
– Simplification of logical expression – K Map or QM method or Boolean
laws and postulates
– Implementation using logic gates

36. Deriving Logical Expressions
• Derivation of logical expressions from truth tables
– sum-of-products (SOP) form
– product-of-sums (POS) form
• SOP form
– Write an AND term for each input combination that
produces a 1 output
• Write the variable if its value is 1; complement if its value 0
– OR the AND terms to get the final expression
• POS form
– Dual of the SOP form

37. Deriving Logical Expressions (cont.)
• 3-input majority function
A B C F
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
• SOP logical expression
• Four product terms
– Because there are 4 rows with
a 1 output
F = A B C + A B C +
A B C + A B C

38. Deriving Logical Expressions (cont.)
• 3-input majority function
A B C F
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
• POS logical expression
• Four sum terms
– Because there are 4 rows with
a 0 output
F = (A + B + C) (A + B + C)
(A + B + C) (A + B + C)

39. Logic function
• Implementing a function from a Boolean
expression X=A+BC’

40. Answer

41. Logic Diagram
• Given logic diagram write logic equation

42. Answer
 work progressively from the inputs to the output
adding logic expressions to the output of each gate in
turn

43. Implementing Logic function
• Given description
• Design a combinational logic circuit with three
input variables that will produce a logic 1
output when more than one input variable are
logic 1 consider input variables A,B and C

44. KARNAUGH MAPS
• Boolean expressions can be graphically depicted and
simplified with the use of Karnaugh maps. In a Karnaugh map
2n
possible minterms of an n-variable Boolean function are
represented by means of separate squares or cells on the
map.
• Karnaugh map for a two, three and four variable Boolean
function

45. • Simplify the following four-variable function:
f (A, B,C,D) f=∑m(0, 1, 4, 5, 7, 8, 9, 12, 13, 15)

46. Adjacencies in Karnaugh maps

47. Don’t Care Conditions
• Functions that include don’t care terms are said to be
incompletely specified functions. The don’t care minterms are
labeled d instead of m.
• Used to minimize Boolean functions and to maximize the
cubes.
• Simplify the given function f (A, B,C) = ∑m(0, 4, 7)+ d(1, 2, 6)

48. • Minimize the following Boolean function using
a Karnaugh map:
• f (A, B, C,D) = ∑m(0, 1, 5, 7, 8, 9, 12, 14, 15) +
d(3, 11, 13)

49. 5 variable function
• Minimize the following Boolean function using
a Karnaugh map:
1. f (A, B, C,D,E) = ∑m(0, 2, 4,6, 9, 11, 13, 15,
17, 21,25,27,29,31) .
2. f (A, B, C,D,E) = ∑m(1,4,8, 10, 11, 20,22, 24,
25, 26)+d(0,12,16,17).

50. Answer
1. BE+A’B’E’+AD’E
2. A’D’E’+B’C’D’+A’BC’D+AB’CE’+ABC’E’+AC’D’

51. Realization of POS expression
• F (A,B,C) = π M (0,1,6,7)
Ans (A+B) (A’+B’)
• F (A,B,C) = π M (0,1,6,7). d(2,3)

52. Design of multiple output circuits
• Design a ckt with 4 input and 3 output which
realise the function
F1(a,b,c,d) = ∑m(11,12,13,14,15)
F2(a,b,c,d) = ∑m(3,7,11,12,13,15)
F3(a,b,c,d) = ∑ m(3,7,12,13,14,15)
• Limitations
• PIs and Essential PIs

53. Equivalent function
• F1 = (ab)’ F2= (ab)’ + ab’ F3 = ab F4 = a’+b
Ans F1 and F2 are equivalent.

54. Realization of basic gates Using NAND gate
NOT gate
• A NOT produces complement of the input. It
can have only one input, to realize NOT tie the
inputs of a NAND gate together. Now it will
work as a NOT gate. Its output is
• Y = (A.A)’
• => Y = (A)’

55. AND gate
• A NAND produces complement of AND gate.
So, if the output of a NAND gate is inverted,
overall output will be that of an AND gate.
• Y = ((A.B)’)’
• => Y = (A.B)

56. OR gate
• The inverted inputs to a NAND gate, obtain OR
operation at output.

57. XOR gate
 The output of a to input X-OR gate is Y = A’B + AB’.
 Realize using basic gates
 Replace basic gate with NAND gate

58. Simplification
• Y = ( (AB’)’ (A’B)’)’
• apply demorgan’s law

59. Realization of basic gates Using NOR gate