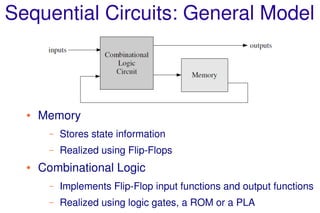
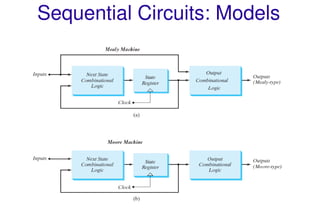
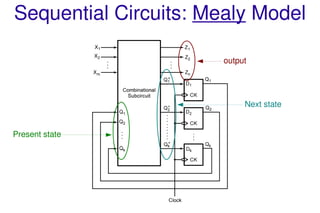
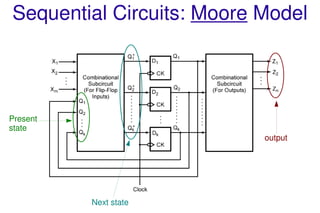
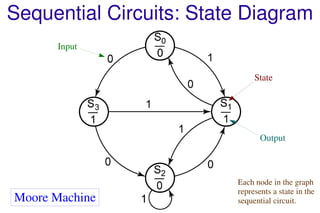
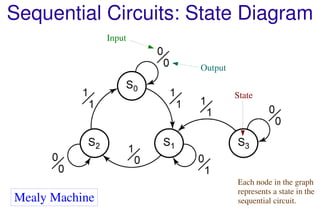
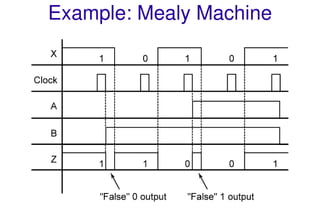
This document discusses sequential logic circuits and their analysis. It defines combinational and sequential logic, and synchronous and asynchronous circuits. There are two main types of sequential logic models - Moore and Mealy machines. Analysis of sequential circuits involves deriving their state tables and state diagrams from the circuit description. Examples show how to analyze circuits using D flip-flops, JK flip-flops, and a serial adder circuit. Multiple input state machines have state tables where the next state depends on all present inputs.