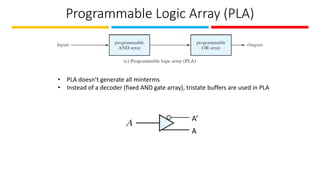
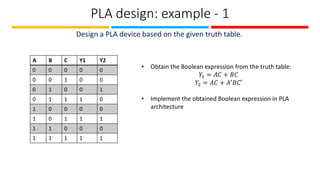
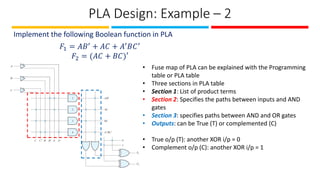
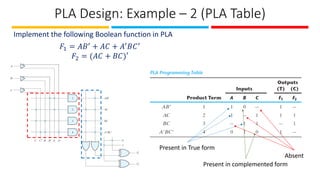
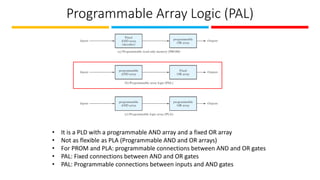
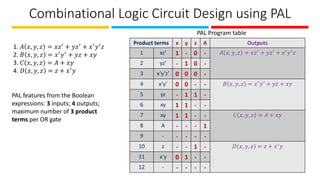
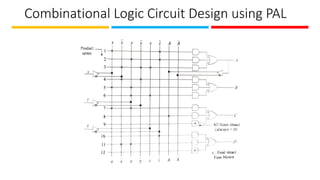
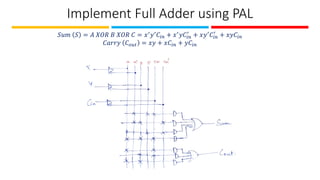
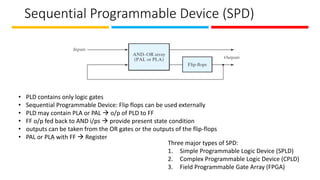
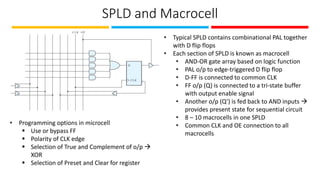
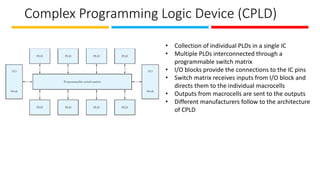
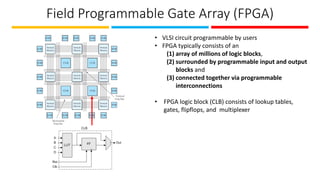
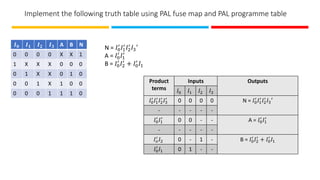
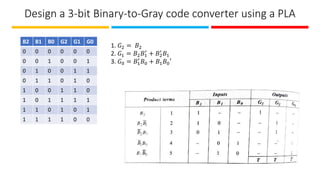
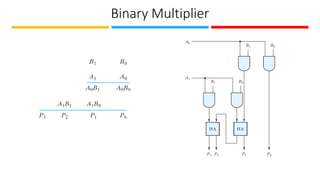
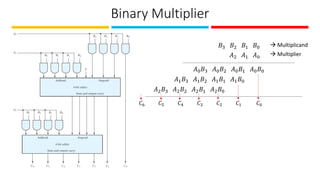
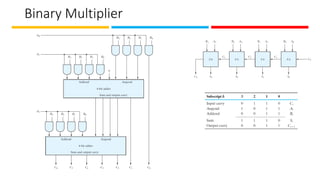
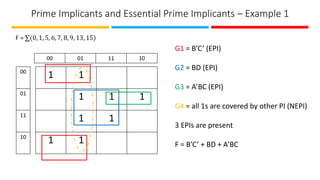
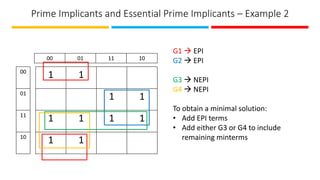
The document discusses the design and implementation of Programmable Logic Arrays (PLAs) and Programmable Array Logic (PAL), including how to obtain boolean expressions from truth tables, and examples of full adder implementations. It also covers Sequential Programmable Devices (SPDs) and their components, such as microcells and the architecture of Complex Programmable Logic Devices (CPLDs) and Field Programmable Gate Arrays (FPGAs). Additionally, the document explains the concepts of prime implicants and essential prime implicants in minimizing boolean functions.