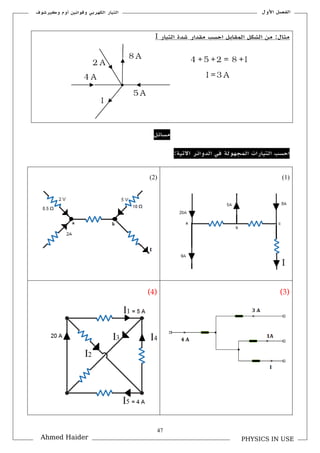
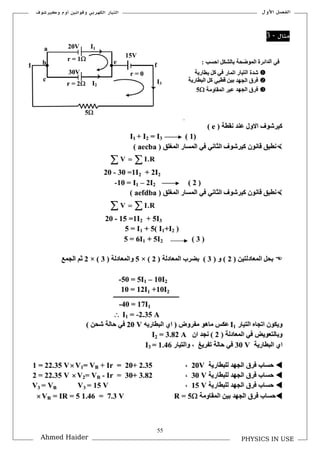
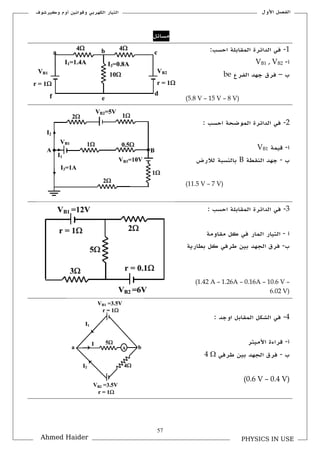
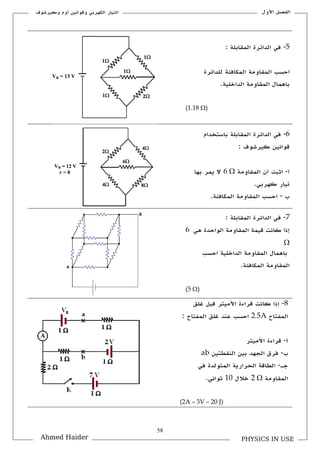
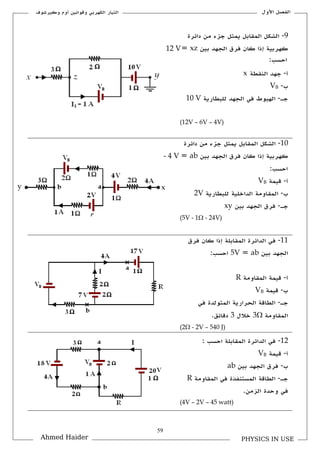
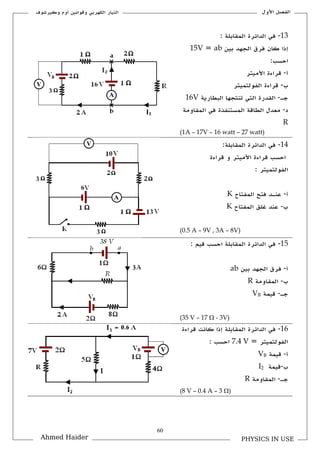
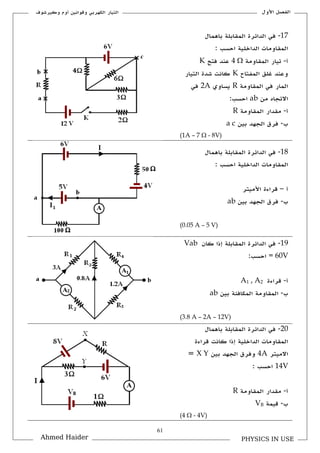
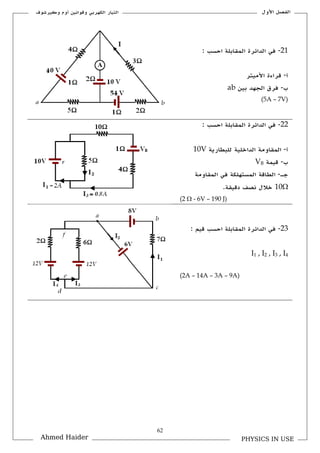
تتناول الوثيقة قوانين كيرشوف المتعلقة بالتيار والجهد في الدوائر الكهربائية، حيث يشرح كيفية استخدام هذه القوانين لحل المسائل المتعلقة بالتوازن الكهربائي. تحوي الوثيقة على صياغات رياضية توضح كيفية جمع التيارات والجهود في الدوائر المغلقة. كما تُعرض تطبيقات عملية لهذه القوانين في مسائل مختلفة.

1. 46
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
‫الكهربية‬ ‫في‬ ‫كيرشوؼ‬ ‫قوانين‬
‫هذاف‬ .‫الجهد‬ ‫قانوف‬ ‫ك‬ ‫التيار‬ ‫قانوف‬ ‫هما‬ ,‫الكهربية‬ ‫في‬ ‫قانونين‬ ‫كيرشوؼ‬ ‫األلماني‬ ‫العالم‬ ‫كضع‬
‫ب‬ ‫المتعللة‬ ‫المسائل‬ ‫حل‬ ‫في‬ ‫يساعداف‬ ‫اللانوناف‬‫ال‬ ‫التي‬ ‫ك‬ ‫المعلدة‬ ‫ك‬ ‫المركبة‬ ‫الكهربية‬ ‫الدكائر‬
.‫أكـ‬ ‫قانوف‬ ‫باستخداـ‬ ‫حلها‬ ‫يمكن‬
‫كيرشوؼ‬ ‫قانوف‬)‫(االكؿ‬:‫للتيار‬
:‫اللانوف‬ ‫نص‬
‫الداخلة‬ ‫التيارات‬ ‫مجموع‬‫عند‬‫نلطة‬‫مغللة‬ ‫كهربية‬ ‫دائرة‬ ‫في‬‫الخارجة‬ ‫التيارات‬ ‫مجموع‬ ‫يساكم‬
.‫منها‬
‫النلط‬ ‫الي‬ ‫الداخل‬ ‫للتيار‬ ‫رمزنا‬ ‫اذا‬ ,‫اخرم‬ ‫بصيغة‬ ‫ك‬‫من‬ ‫الخارج‬ ‫كالتيار‬ ) + ( ‫موجب‬ ‫بعالمة‬ ‫ة‬
( ‫بعالمة‬ ‫النلطة‬-‫ف‬ ,)‫إ‬:‫التالية‬ ‫بالصيغة‬ ‫اللانوف‬ ‫هذا‬ ‫نصيغ‬ ‫أف‬ ‫يمكن‬ ‫ننا‬
‫الجبرم‬ ‫المجموع‬‫ل‬‫نلطة‬ ‫عند‬ ‫لتيارات‬‫مغللة‬ ‫دائرة‬ ‫في‬.‫صفر‬ ‫يساكم‬
‫ن‬‫ا‬‫رياضي‬ ‫اللانوف‬ ‫هذا‬ ‫نكتب‬ ‫أف‬ ‫يمكن‬ ‫التالي‬ ‫بالرسم‬ ‫باالستعانة‬ ‫ك‬:‫التالية‬ ‫بالصيغة‬
 Iin =  Io or  I = 0
‫علل‬
1.‫يسمى‬‫ب‬ ‫األكؿ‬ ‫اللانوف‬‫الشحنة‬ ‫حفظ‬ ‫لانوف‬
‫ألف‬‫الشحنة‬ ‫ملدار‬ ‫نفس‬ ‫هو‬ ,‫ما‬ ‫نلطة‬ ‫الى‬ ‫الداخلة‬ ‫الكهربية‬ ‫الشحنة‬ ‫ملدار‬
‫النلطة‬ ‫هذق‬ ‫من‬ ‫الخارجة‬ ‫الكهربية‬‫تساكم‬ )‫باألمبير‬ (‫التيار‬ ‫شدة‬ ‫أف‬ ‫(كمعلوـ‬
‫مع‬ ‫ملطع‬ ‫تعبر‬ ‫التي‬ ) ‫بالكولوـ‬ ( ‫الشحنات‬ ‫ملدار‬) ‫ثانية‬ ( ‫الزمن‬ ‫كحدة‬ ‫في‬ ‫ين‬
2.‫التوازم‬ ‫دكائر‬ ‫في‬ ‫للتيار‬ ‫كيرشوؼ‬ ‫قانوف‬ ‫يستخدـ‬
‫في‬ ‫يتجزأ‬ ‫التيار‬ ‫الف‬‫إلى‬ ‫ها‬.‫فركع‬ ‫عدة‬

2. 47
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
‫التيار‬ ‫شدة‬ ‫ملدار‬ ‫احسب‬ ‫الملابل‬ ‫الشكل‬ ‫من‬ :‫مثاؿ‬I
‫مسائل‬
‫االتية‬ ‫الدكائر‬ ‫في‬ ‫المجهولة‬ ‫التيارات‬ ‫احسب‬:
(1)(2)
(3)(4)

3. 48
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
‫كيرشوؼ‬ ‫قانوف‬‫الثاني‬:‫للجهد‬
:‫اللانوف‬ ‫نص‬
‫دائرة‬ ‫في‬ ‫الكهربية‬ ‫الدافعة‬ ‫لللوة‬ ‫الجبرم‬ ‫المجموع‬‫مغللة‬‫يسا‬‫لفركؽ‬ ‫الجبرم‬ ‫المجموع‬ ‫كم‬
‫الجهد‬.‫الدائرة‬ ‫في‬
:‫اخرل‬ ‫بصيغة‬ ‫اللانوف‬ ‫هذا‬ ‫يصاغ‬ ‫أف‬ ‫كيمكن‬
‫الجبرم‬ ‫المجموع‬‫ا‬ ‫لفركؽ‬‫صف‬ ‫يساكم‬ ‫مغلق‬ ‫مسار‬ ‫في‬ ‫لجهد‬‫را‬
:‫التالية‬ ‫بالصيغة‬ ‫رياضيا‬ ‫اللانوف‬ ‫هذا‬ ‫نكتب‬ ‫أف‬ ‫يمكن‬ ‫التالي‬ ‫بالرسم‬ ‫باالستعانة‬
VB =  I R
(VB)1 + (VB)2 = I R1 + I R2
(VB)1 + (VB)2 – I R1 - I R2 = 0
‫الطاقة‬ ‫تساكم‬ ‫الشحنات‬ ‫لوحدة‬ ‫المكتسبة‬ ‫الطاقة‬ ‫أف‬ ‫أم‬ ‫الطاقة‬ ‫حفظ‬ ‫للانوف‬ ‫تطبيق‬ ‫اللانوف‬ ‫كهذا‬
‫ا‬ ‫لوحدة‬ ‫المفلودة‬‫لشحنات‬)‫(علل‬
‫ت‬ ‫ال‬ ‫ك‬ ‫تستحدث‬ ‫ال‬ ‫الطاقة‬ ‫الف‬‫فنى‬‫الطاقة‬ ‫مثال‬ ,‫آخر‬ ‫الى‬ ‫شكل‬ ‫من‬ ‫تتحوؿ‬ ‫لكنها‬ ‫ك‬
‫ك‬ ‫حرارية‬ ‫طاقة‬ ‫أك‬ ‫ملاكمة‬ ‫في‬ ‫حرارية‬ ‫طاقة‬ ‫الى‬ ‫تتحوؿ‬ ‫أف‬ ‫يمكن‬ ‫البطارية‬ ‫في‬ ‫الكيميائية‬
.‫مصباح‬ ‫في‬ ‫ضوئية‬
‫أف‬ ‫كمعلوـ‬:
‫لت‬ )‫(بالجوؿ‬ ‫المبذكؿ‬ ‫الشغل‬ ‫يساكم‬ ,‫نلطتين‬ ‫بين‬ ,) ‫بالفولت‬ ( ‫الجهد‬‫الشحنات‬ ‫كحدة‬ ‫حريك‬
)‫النلطتين‬ ‫هاتين‬ ‫بين‬ )‫(بالكولوـ‬
‫الليم‬ ‫على‬ ‫للحصوؿ‬ ‫حلها‬ ‫يمكن‬ ‫رياضية‬ ‫معادالت‬ ‫نكوف‬ ‫أف‬ ‫يمكن‬ ‫كيرشوؼ‬ ‫قوانين‬ ‫باستخداـ‬ ‫ك‬
.‫ايجادها‬ ‫المراد‬

4. 49
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
‫االشارات‬ ‫قاعدة‬
‫الساعة‬ ‫علارب‬ ‫مع‬‫الساعة‬ ‫علارب‬ ‫عكس‬
‫اللطب‬ ‫من‬ ‫فرضناق‬ ‫الذم‬ ‫المسار‬ ‫كاف‬ ‫إذا‬
‫الموجب‬ ‫اللطب‬ ‫إلى‬ ‫السالب‬‫فإف‬ ‫البطارية‬ ‫داخل‬
VB‫موجبة‬ ‫تكوف‬
‫اللطب‬ ‫من‬ ‫فرضناق‬ ‫الذم‬ ‫المسار‬ ‫كاف‬ ‫إذا‬
‫البطارية‬ ‫داخل‬ ‫السالب‬ ‫اللطب‬ ‫إلى‬ ‫الموجب‬
‫فإف‬VB‫سالبة‬ ‫تكوف‬
‫نفس‬ ‫هو‬ ‫فرضناق‬ ‫الذم‬ ‫المسار‬ ‫اتجاق‬ ‫كاف‬ ‫إذا‬
‫فرؽ‬ ‫فإف‬ ‫ما‬ ‫ملاكمة‬ ‫في‬ ‫المار‬ ‫في‬ ‫التيار‬ ‫اتجاق‬
‫الجهد‬‫موجب‬ ‫يكوف‬ ‫الملاكمة‬ ‫هذق‬ ‫طرفي‬ ‫بين‬
‫عكس‬ ‫هو‬ ‫فرضناق‬ ‫الذم‬ ‫المسار‬ ‫اتجاق‬ ‫كاف‬ ‫إذا‬
‫فرؽ‬ ‫فإف‬ ‫ما‬ ‫ملاكمة‬ ‫في‬ ‫المار‬ ‫في‬ ‫التيار‬ ‫اتجاق‬
.‫سالب‬ ‫يكوف‬ ‫الملاكمة‬ ‫هذق‬ ‫طرفي‬ ‫بين‬ ‫الجهد‬
‫معادالت‬ ‫تكوين‬ ‫خطوات‬
‫أف‬ ‫تعلم‬ ‫أف‬ ‫البد‬ ‫المعادالت‬ ‫تكوين‬ ‫قبل‬:
‫ال‬ ‫عدد‬‫المجاهيل‬ ‫عدد‬ = ‫معادالت‬
‫المجاهيل‬ ‫عدد‬ = ‫المغللة‬ ‫المسارات‬ ‫عدد‬–1)‫ن‬‫ا‬‫(غالب‬
1-‫نفرض‬.‫المسألة‬ ‫آخر‬ ‫إلى‬ ‫بها‬ ‫كألتزـ‬ ‫الدائرة‬ ‫أفرع‬ ‫جميع‬ ‫في‬ ‫للتيار‬ ‫عشوائية‬ ‫اتجاهات‬
2-‫األكؿ‬ ‫اللانوف‬ ‫كطبق‬ ‫تجمع‬ ‫أك‬ ‫تفرع‬ ‫نلطة‬ ‫حدد‬‫األكلى‬ ‫المعادلة‬
3-‫السا‬ ‫من‬ ‫بطارية‬ ‫كل‬ ‫في‬ ‫التيار‬ ‫اتجاق‬ ‫ضع‬:‫يلي‬ ‫كما‬ )‫البطارية‬ ‫(فوؽ‬ ‫للموجب‬ ‫لب‬

5. 51
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
4-‫نفرض‬)‫الساعة‬ ‫علارب‬ ‫عكس‬ ‫أك‬ ‫الساعة‬ ‫علارب‬ ‫(مع‬ ‫له‬ ‫عشوائي‬ ‫اتجاق‬ ‫كضع‬ ‫مغلق‬ ‫مسار‬
5-: ‫الثاني‬ ‫كيرشوؼ‬ ‫قانوف‬ ‫طبق‬
VB =  I R
: ‫البطاريات‬ ‫األيسر‬ ‫الطرؼ‬
‫في‬ ‫فرضناق‬ ‫كما‬ ‫البطارية‬ ‫في‬ ‫التيار‬ ‫اتجاق‬ ‫كاف‬ ‫إذا‬( ‫رقم‬3)‫يكػػوف‬ ‫المسار‬ ‫اتجاق‬ ‫مع‬+VB
‫في‬ ‫فرضناق‬ ‫كما‬ ‫البطارية‬ ‫في‬ ‫التيار‬ ‫اتجاق‬ ‫كاف‬ ‫إذا‬( ‫رقم‬3)‫عك‬‫ػ‬‫يكوف‬ ‫المسار‬ ‫اتجاق‬ ‫س‬- VB
: ‫الدائرة‬ ‫جهد‬ ‫فركؽ‬ ‫األيمن‬ ‫الطرؼ‬
‫يكػػوف‬ ‫المسار‬ ‫اتجاق‬ ‫مع‬ ‫فرضناق‬ ‫كما‬ ‫الملاكمة‬ ‫في‬ ‫التيار‬ ‫اتجاق‬ ‫كاف‬ ‫إذا‬+ I R
‫ال‬ ‫اتجاق‬ ‫عكس‬ ‫فرضناق‬ ‫كما‬ ‫الملاكمة‬ ‫في‬ ‫التيار‬ ‫اتجاق‬ ‫كاف‬ ‫إذا‬‫يكوف‬ ‫مسار‬- I R
6-‫الحاسبة‬ ‫اآللة‬ ‫باستخداـ‬ / ‫ن‬‫ا‬‫رياضي‬ ‫المعادالت‬ ‫تحل‬.
7-‫سالب‬ ‫التيارات‬ ‫أحد‬ ‫كاف‬ ‫إذا‬.‫المفركض‬ ‫االتجاق‬ ‫عكس‬ ‫التيار‬ ‫هذا‬ ‫اتجاق‬ ‫يكوف‬
:‫الحظ‬
‫نحسب‬ ‫توازم‬ ‫أك‬ ‫توالي‬ ‫ملاكمات‬ ‫في‬ ‫لو‬‫الملاكمة‬‫المكافئة‬.‫لهما‬
‫بجوارها‬ ‫توضع‬ ‫لبطارية‬ ‫داخلية‬ ‫ملاكمة‬ ‫في‬ ‫لو‬.
‫أمثلة‬‫محلولة‬
‫مثاؿ‬-1
‫الملاكمات‬ ‫في‬ ‫المارة‬ ‫التيارات‬ ‫ملادير‬ ‫أحسب‬R3, R2, R1:‫التالية‬ ‫الكهربية‬ ‫الدائرة‬ ‫في‬
(‫بإهماؿ‬) ‫للمصادر‬ ‫الداخلية‬ ‫الملاكمة‬

6. 51
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
‫الدائرة‬ ‫فركع‬ ‫كل‬ ‫في‬ ‫للتيارات‬ ‫اتجاهات‬ ‫عشوائية‬ ‫بصورة‬ ‫نضع‬: ‫بالشكل‬ ‫كما‬
‫تفرع‬ ‫نلطة‬ ‫نحدد‬‫نلطتين‬ ‫يوجد‬ ‫الدائرة‬ ‫هذق‬ ‫في‬‫هي‬ ‫فلط‬(c , f)
‫النلطة‬ ‫عند‬ ‫للتيار‬ ‫كيرشوؼ‬ ‫للانوف‬ ‫تطبيلا‬ ‫األكلى‬ ‫المعادلة‬c
I3 = I 1+ I 2 ……… (1)
‫النلطة‬ ‫عند‬ ‫معادلة‬ ‫لكتابة‬ ‫داعي‬ ‫ال‬f‫النلطة‬ ‫عند‬ ‫المعادلة‬ ‫نفس‬ ‫ألنها‬c
‫مغلق‬ ‫مسار‬ ‫كنحدد‬ ‫البطاريات‬ ‫في‬ ‫التيار‬ ‫اتجاق‬ ‫نضع‬‫المغ‬ ‫للمسار‬‫لق‬abcfa‫ب‬ ‫له‬ ‫رمزنا‬ ‫الذم‬ ‫ك‬‫ػ‬
loop1‫الساعة‬ ‫علارب‬ ‫مع‬ ‫اتجاهه‬ ‫الرسم‬ ‫في‬ ‫ظاهر‬ ‫كما‬ ‫هو‬ ‫ك‬‫ب‬‫للجهد‬ ‫كيرشوؼ‬ ‫قانوف‬ ‫تطبيق‬
:‫الثانية‬ ‫المعادلة‬ ‫على‬ ‫نحصل‬
VB =  I R
6 – 4 = 3I 1 – 2I2  2 = 3I 1 – 2I2 ……….. (2)
‫الحظ‬:
‫الملاكمة‬ ‫طرفي‬ ‫بين‬ ‫الجهد‬ ‫فرؽ‬3‫موجب‬‫ا‬ ‫اتجاق‬ ‫الف‬‫المار‬ ‫لتيار‬‫المسار‬ ‫اتجاق‬ ‫نفس‬ ‫هو‬ ‫فيها‬loop1.
‫الملاكمة‬ ‫طرفي‬ ‫بين‬ ‫الجهد‬ ‫فرؽ‬2‫سالب‬‫المار‬ ‫التيار‬ ‫اتجاق‬ ‫الف‬‫المسار‬ ‫اتجاق‬ ‫عكس‬ ‫فيها‬loop1.
‫المصدر‬ ‫جهد‬ ‫أف‬ ‫الحظ‬ ‫ككذلك‬V6‫المسار‬ ‫اتجاق‬ ‫نفس‬ ‫هو‬ ‫منه‬ ‫المتولد‬ ‫التيار‬ ‫اتجاق‬ ‫ألف‬ ‫موجب‬loop1.
‫المصدر‬ ‫جهد‬ ‫ك‬V4‫اتجاق‬ ‫ألف‬ ‫سالب‬‫المسار‬ ‫اتجاق‬ ‫عكس‬ ‫منه‬ ‫المتولد‬ ‫التيار‬loop1.
‫المغلق‬ ‫للمسار‬ ‫للجهد‬ ‫كيرشوؼ‬ ‫للانوف‬ ‫تطبيلا‬ ‫الثالثة‬ ‫المعادلة‬fcdef‫ب‬ ‫له‬ ‫رمزنا‬ ‫الذم‬ ‫ك‬‫ػ‬
loop2‫الساعة‬ ‫علارب‬ ‫مع‬ ‫اتجاهه‬ ‫الرسم‬ ‫في‬ ‫ظاهر‬ ‫كما‬ ‫كهو‬.
4 = 2 I2 + 8 I 3 ……….. (3)
( ‫هي‬ ‫مستللة‬ ‫معادالت‬ ‫ثالثة‬ ‫لدينا‬ ‫كاآلف‬1( ,)2( ,)3‫كايجاد‬ ‫المسألة‬ ‫نحل‬ ‫أف‬ ‫يمكن‬ ‫منها‬ ‫التي‬ ‫ك‬ )
.‫المطلوبة‬ ‫الثالثة‬ ‫التيارات‬ ‫قيم‬
:‫الحل‬

7. 52
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
‫الرياضي‬ ‫الحل‬‫الحاسبة‬ ‫اآللة‬ ‫باستخداـ‬
‫للتيار‬ ‫نعوض‬I3( ‫المعادلة‬ ‫من‬1( ‫المعادلة‬ ‫في‬ )3)
:‫على‬ ‫لنحصل‬
4 = 2 I 2 + 8 ( I 1+ I 2 )
2 I 2 + 8 I 1 +8 I 2 = 4
10 I 2 + 8 I 1 = 4 ……….(4)
‫الم‬ ‫ضع‬( ‫عادلة‬2( ‫المعادلة‬ ‫تحت‬ )4)
10 I 2 + 8 I 1 = 4 ……(4)
3I 1 – 2I2 = 2 …….. (2)
‫ب‬( ‫المعادلة‬ ‫ضرب‬2)×5
10 I 2 + 8 I 1 = 4 ……(4)
10 I2 + 15I 1 = 11 ….(2)-
‫بالجمع‬
23 I1 = 14
A0.608=1I
‫عن‬ ‫بالتعويض‬I1‫المعادلة‬ ‫في‬(4)‫على‬ ‫للحصوؿ‬
‫قيمة‬I2
10 I 2 + 8 I 1 = 4 ……(4)
10 I 2 + 8 (0.608) = 4
10 I 2 + 4.864 = 4
10 I 2 = 4 – 4.864
10 I 2 = – 0.864
A0.0864–=2I
‫التيار‬ ‫قيمة‬ ‫أف‬ ‫(الحظ‬I 2‫أف‬ ‫يعني‬ ‫هذا‬ ‫ك‬ ‫سالبة‬
‫الرسم‬ ‫في‬ ‫كضعناق‬ ‫الذم‬ ‫االتجاق‬‫لػ‬I2‫صحيحا‬ ‫ليس‬
.)‫االتجاق‬ ‫هذا‬ ‫عكس‬ ‫الصحيح‬ ‫بل‬
‫اآل‬ ‫ك‬‫التيار‬ ‫قيمة‬ ‫نعوض‬ ‫ف‬I1‫التيار‬ ‫ك‬I2‫المعادلة‬ ‫في‬
(1‫التيار‬ ‫قيمة‬ ‫اليجاد‬ )I3
I3 = I 1+ I 2 ……… (1)
I 3 = 0.608 - 0.0864 = 0.5216
:‫الثالثة‬ ‫المعادالت‬
I 1+ I 2 = I3 …….. (1)
3I 1 – 2I2 = 2…….. (2)
2 I2 + 8 I 3 = 4 ….. (3)
1-‫ن‬‫ضع‬‫المعادالت‬‫صورة‬ ‫في‬‫(أم‬ ‫صفرية‬
‫حد‬ ‫منها‬ ‫يختفي‬ ‫التي‬ ‫كالمعادلة‬ )‫صفر‬ ‫تساكم‬
:‫كاآلتي‬ ‫صفر‬ ‫مكانه‬ ‫يوضع‬
I 1+ I 2 - I3 + 1 = 1 …….. (1)
3I 1 – 2I2 + 0 – 2 = 0…….. (2)
0 + 2 I2 + 8 I 3 – 4 = 0 ….. (3)
2-:‫الحاسبة‬ ‫اآللة‬ ‫على‬ ‫المعامالت‬ ‫ندخل‬ ‫ثم‬
: ‫على‬ ‫فنحصل‬
I1 = 0.608 A
I2 = - 0.0864 A
‫المفركض‬ ‫االتجاق‬ ‫عكس‬ ‫الصحيح‬ ‫اتجاهه‬ ‫أم‬
I3 = 0.5216 A

8. 53
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
‫مثاؿ‬–2
‫الملاكمات‬ ‫في‬ ‫المارة‬ ‫التيارات‬ ‫ملادير‬ ‫أحسب‬R3, R2, R1:‫التالية‬ ‫الكهربية‬ ‫الدائرة‬ ‫في‬
) ‫للمصادر‬ ‫الداخلية‬ ‫الملاكمة‬ ‫تجاهل‬ :‫تنبيه‬ (
:‫الحل‬
‫ب‬‫تطبيق‬‫ال‬ ‫عند‬ ‫للتيار‬ ‫كيرشوؼ‬ ‫قانوف‬‫نلطة‬c:
I 1 = I 2 + I 3 ….…(1)
‫على‬ ‫الثاني‬ ‫كيرشوؼ‬ ‫قانوف‬ ‫بتطبيق‬loop1
10 – 3 = 20 I 1 + 6 I 2
7 = 20 I 1 + 6 I 2 …….. (2)
‫على‬ ‫الثاني‬ ‫كيرشوؼ‬ ‫قانوف‬ ‫بتطبيق‬loop2
8 – 3 = 6 I 2 - 10 I 3
5 = 6 I 2 – 10 I 3 …….. (3)

9. 54
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
( ‫المعادلة‬ ‫من‬1‫على‬ ‫نحصل‬ )
I 3 = I 1 – I 2
‫نعوض‬I 3( ‫المعادلة‬ ‫في‬3‫على‬ ‫لنحصل‬ )
5 = 6 I 2 – 10 (I1 – I2)  5 = 6 I 2 – 10 I1 +10 I2
5 = 16 I 2 – 10 I1………(4)
‫المعادلتين‬ ‫بحل‬(2, 4)‫المعادلة‬ ‫بضرب‬(4)×2
32 I 2 – 20 I1 = 10
6 I 2 + 20 I 1 = 7
38 I2 = 17
A0.447=2I
‫لل‬ ‫نعوض‬‫يمة‬I 2( ‫المعادلة‬ ‫في‬4‫على‬ ‫لنحصل‬ )
5 + 10 I 1 – 16 X 0.447 = 0
5 + 10 I 1 – 7.152 = 0  10 I 1 – 2.152 = 0
A0.215=1I
( ‫المعادلة‬ ‫في‬ ‫نعوض‬1‫اليجاد‬ )I 3
I 3 = I 1 – I 2
I 3 = 0.215 – 0.447
.A0.232–=3I
‫أم‬‫ا‬ ‫أف‬‫تجاق‬I 3‫ا‬‫المفركض‬ ‫االتجاق‬ ‫عكس‬ ‫لصحيح‬
‫الحل‬ ‫من‬ ‫للتأكد‬ ‫الحاسبة‬ ‫اآللة‬ ‫استخدـ‬

10. 55
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
‫مثاؿ‬-3

11. 56
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
‫مثاؿ‬–4
------------------------------------------------------
‫ك‬ ‫تجرع‬ ‫ساعة‬ ‫التعلم‬ ‫مر‬ ‫يذؽ‬ ‫لم‬ ‫من‬‫أ‬‫العمر‬ ‫طوؿ‬ ‫الجهل‬ ‫س‬

12. 57
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
‫مسائل‬.
1-‫ال‬ ‫في‬:‫احسب‬ ‫الملابلة‬ ‫دائرة‬
‫أ‬-VB1 , VB2
‫ب‬–‫ف‬‫الفرع‬ ‫جهد‬ ‫رؽ‬be
(5.8 V – 15 V – 8 V)
2-‫اح‬ ‫الموضحة‬ ‫الدائرة‬ ‫في‬‫س‬‫ب‬:
‫أ‬-‫قيمة‬VB1
‫ب‬-‫النلطة‬ ‫جهد‬B‫لالرض‬ ‫بالنسبة‬
(11.5 V – 7 V)
3-‫ف‬: ‫احسب‬ ‫الملابلة‬ ‫الدائرة‬ ‫ي‬
‫أ‬-‫ملاكمة‬ ‫كل‬ ‫في‬ ‫المار‬ ‫التيار‬
‫ب‬-‫بطارية‬ ‫كل‬ ‫طرفي‬ ‫بين‬ ‫الجهد‬ ‫فرؽ‬
(1.42 A – 1.26A – 0.16A – 10.6 V –
6.02 V)
4-‫ا‬ ‫الملابل‬ ‫الشكل‬ ‫في‬‫كجد‬:
‫أ‬-‫األميتر‬ ‫قراءة‬
‫ب‬-‫طرفي‬ ‫بين‬ ‫الجهد‬ ‫فرؽ‬4 
(0.6 V – 0.4 V)

13. 58
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
5-: ‫الملابلة‬ ‫الدائرة‬ ‫في‬
‫المكافئة‬ ‫الملاكمة‬ ‫احسب‬‫للدائرة‬
‫الداخلية‬ ‫الملاكمة‬ ‫باهماؿ‬.
(1.18 )
6-‫باستخداـ‬ ‫الملابلة‬ ‫الدائرة‬ ‫في‬
‫كيرشوؼ‬ ‫قوانين‬:
‫أ‬-‫الملاكمة‬ ‫أف‬ ‫اثبت‬6 ‫بها‬ ‫يمر‬ ‫ال‬
.‫كهربي‬ ‫تيار‬
‫ب‬-.‫المكافئة‬ ‫الملاكمة‬ ‫احسب‬
7-: ‫الملابلة‬ ‫الدائرة‬ ‫في‬
‫هي‬ ‫الواحدة‬ ‫الملاكمة‬ ‫قيمة‬ ‫كانت‬ ‫إذا‬6

‫الداخلية‬ ‫الملاكمة‬ ‫باهماؿ‬‫احسب‬
.‫المكافئة‬ ‫الملاكمة‬
(5 )
8-‫غ‬ ‫قبل‬ ‫األميتر‬ ‫قراءة‬ ‫كانت‬ ‫إذا‬‫لق‬
‫المفتاح‬2.5A: ‫المفتاح‬ ‫غلق‬ ‫عند‬ ‫احسب‬
‫أ‬-‫األميتر‬ ‫قراءة‬
‫ب‬-‫النلطتين‬ ‫بين‬ ‫الجهد‬ ‫فرؽ‬ab
‫جػ‬-‫في‬ ‫المتولدة‬ ‫الحرارية‬ ‫الطاقة‬
‫الملاكمة‬2 ‫خالؿ‬11.‫ثواني‬
(2A – 3V – 20 J)

14. 59
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
9-‫دائرة‬ ‫من‬ ‫جزء‬ ‫يمثل‬ ‫الملابل‬ ‫الشكل‬
‫بين‬ ‫الجهد‬ ‫فرؽ‬ ‫كاف‬ ‫إذا‬ ‫كهربية‬xz=12 V
:‫احسب‬
‫أ‬-‫ال‬ ‫جهد‬‫نلطة‬x
‫ب‬-VB
‫جػ‬-‫للبطارية‬ ‫الجهد‬ ‫في‬ ‫الهبوط‬10 V
(12V – 6V – 4V)
11-‫دائرة‬ ‫من‬ ‫جزء‬ ‫يمثل‬ ‫الملابل‬ ‫الشكل‬
‫بين‬ ‫الجهد‬ ‫فرؽ‬ ‫كاف‬ ‫إذا‬ ‫كهربية‬ab=- 4 V
:‫احسب‬
‫أ‬-‫قيمة‬VB
‫ب‬-‫للبطارية‬ ‫الداخلية‬ ‫الملاكمة‬2V
‫جػ‬-‫بين‬ ‫الجهد‬ ‫فرؽ‬xy
(5V - 1 - 24V)
11-‫ف‬‫فرؽ‬ ‫كاف‬ ‫إذا‬ ‫الملابلة‬ ‫الدائرة‬ ‫ي‬
‫بين‬ ‫الجهد‬ab=5V:‫احسب‬
‫أ‬-‫الملاكمة‬ ‫قيمة‬R
‫ب‬-‫قيمة‬VB
‫جػ‬-‫في‬ ‫المتولدة‬ ‫الحرارية‬ ‫الطاقة‬
‫الملاكمة‬3‫خالؿ‬3.‫دقائق‬
(2 - 2V – 540 J)
12-: ‫احسب‬ ‫الملابلة‬ ‫الدائرة‬ ‫في‬
‫أ‬-‫قيمة‬VB
‫ب‬-‫بين‬ ‫الجهد‬ ‫فرؽ‬ab
‫جػ‬-‫الملا‬ ‫في‬ ‫المستنفذة‬ ‫الطاقة‬‫كمة‬R
.‫الزمن‬ ‫كحدة‬ ‫في‬
(4V – 2V – 45 watt)
y

15. 61
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
13-‫الملابلة‬ ‫الدائرة‬ ‫في‬:
‫بين‬ ‫الجهد‬ ‫فرؽ‬ ‫كاف‬ ‫إذا‬ab=15V
:‫احسب‬
‫أ‬-‫األميتر‬ ‫قراءة‬
‫ب‬-‫الفولتميتر‬ ‫قراءة‬
‫جػ‬-‫البطارية‬ ‫تنتجها‬ ‫التي‬ ‫اللدرة‬16V
‫د‬-‫الملاكمة‬ ‫في‬ ‫المستنفذة‬ ‫الطاقة‬ ‫معدؿ‬
R
(1A – 17V – 16 watt – 27 watt)
14-:‫الملابلة‬ ‫الدائرة‬ ‫في‬
‫قراءة‬ ‫ك‬ ‫األميتر‬ ‫قراءة‬ ‫احسب‬
: ‫الفولتميتر‬
‫أ‬-‫عن‬‫ػ‬‫المفتاح‬ ‫فتح‬ ‫د‬K
‫ب‬-‫المفتاح‬ ‫غلق‬ ‫عند‬K
(0.5 A – 9V , 3A – 8V)
15-: ‫قيم‬ ‫احسب‬ ‫الملابلة‬ ‫الدائرة‬ ‫في‬
‫أ‬-‫بين‬ ‫الجهد‬ ‫فرؽ‬ab
‫ب‬-‫الملاكمة‬R
‫جػ‬-‫قيمة‬VB
(35 V – 17  - 3V)
16-‫الدائرة‬ ‫في‬‫قراءة‬ ‫كانت‬ ‫إذا‬ ‫الملابلة‬
= ‫الفولتميتر‬7.4 V: ‫احسب‬
‫أ‬-‫قيمة‬VB
‫ب‬-‫قيمة‬I2
‫جػ‬-‫الملاكمة‬R
(8 V – 0.4 A – 3 )

16. 61
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
17-‫باهماؿ‬ ‫الملابلة‬ ‫الدائرة‬ ‫في‬
: ‫احسب‬ ‫الداخلية‬ ‫الملاكمات‬
‫أ‬-‫الملاكمة‬ ‫تيار‬4 ‫فتح‬ ‫عند‬K
‫المفتاح‬ ‫غلق‬ ‫كعند‬K‫التيار‬ ‫شدة‬ ‫كانت‬
‫الملاكمة‬ ‫في‬ ‫المار‬R‫يسا‬‫كم‬2A‫في‬
‫من‬ ‫االتجاق‬ab:‫احسب‬
‫أ‬-‫الملاكمة‬ ‫ملدار‬R
‫ب‬-‫بين‬ ‫الجهد‬ ‫فرؽ‬a c
(1A – 7  - 8V)
18-‫باهماؿ‬ ‫الملابلة‬ ‫الدائرة‬ ‫في‬
: ‫احسب‬ ‫الداخلية‬ ‫الملاكمات‬
‫أ‬–‫األميتر‬ ‫قراءة‬
‫ب‬-‫بين‬ ‫الجهد‬ ‫فرؽ‬ab
(0.05 A – 5 V)
19-‫كاف‬ ‫إذا‬ ‫الملابلة‬ ‫الدائرة‬ ‫في‬Vab
= 60V:‫احسب‬
‫أ‬-‫قراءة‬A1 , A2
‫ب‬-‫بين‬ ‫المكافئة‬ ‫الملاكمة‬ab
(3.8 A – 2A – 12V)
21-‫باهماؿ‬ ‫الملابلة‬ ‫الدائرة‬ ‫في‬
‫قراءة‬ ‫كانت‬ ‫إذا‬ ‫الداخلية‬ ‫الملاكمات‬
‫االميتر‬4A‫بين‬ ‫الجهد‬ ‫كفرؽ‬X Y=
14V: ‫احسب‬
‫أ‬-‫الملاكمة‬ ‫ملدار‬R
‫ب‬-‫قيمة‬VB
(4  - 4V)

17. 62
‫األكؿ‬ ‫الفصل‬‫ككيرشوؼ‬ ‫أكـ‬ ‫كقوانين‬ ‫الكهربي‬ ‫التيار‬
PHYSICS IN USEAhmed Haider
21-: ‫احسب‬ ‫الملابلة‬ ‫الدائرة‬ ‫في‬
‫أ‬-‫ق‬‫األميتر‬ ‫راءة‬
‫ب‬-‫بين‬ ‫الجهد‬ ‫فرؽ‬ab
(5A – 7V)
22-: ‫احسب‬ ‫الملابلة‬ ‫الدائرة‬ ‫في‬
‫أ‬-‫للبطارية‬ ‫الداخلية‬ ‫الملاكمة‬10V
‫ب‬-‫قيمة‬VB
‫جػ‬-‫الملاكمة‬ ‫في‬ ‫المستهلكة‬ ‫الطاقة‬
10.‫دقيلة‬ ‫نص‬ ‫خالؿ‬
(2  - 6V – 190 J)
23-: ‫قيم‬ ‫احسب‬ ‫الملابلة‬ ‫الدائرة‬ ‫في‬
I1 , I2 , I3 , I4
(2A – 14A – 3A – 9A)