Uploaded byInfinity Tech Solutions
Network security CS2
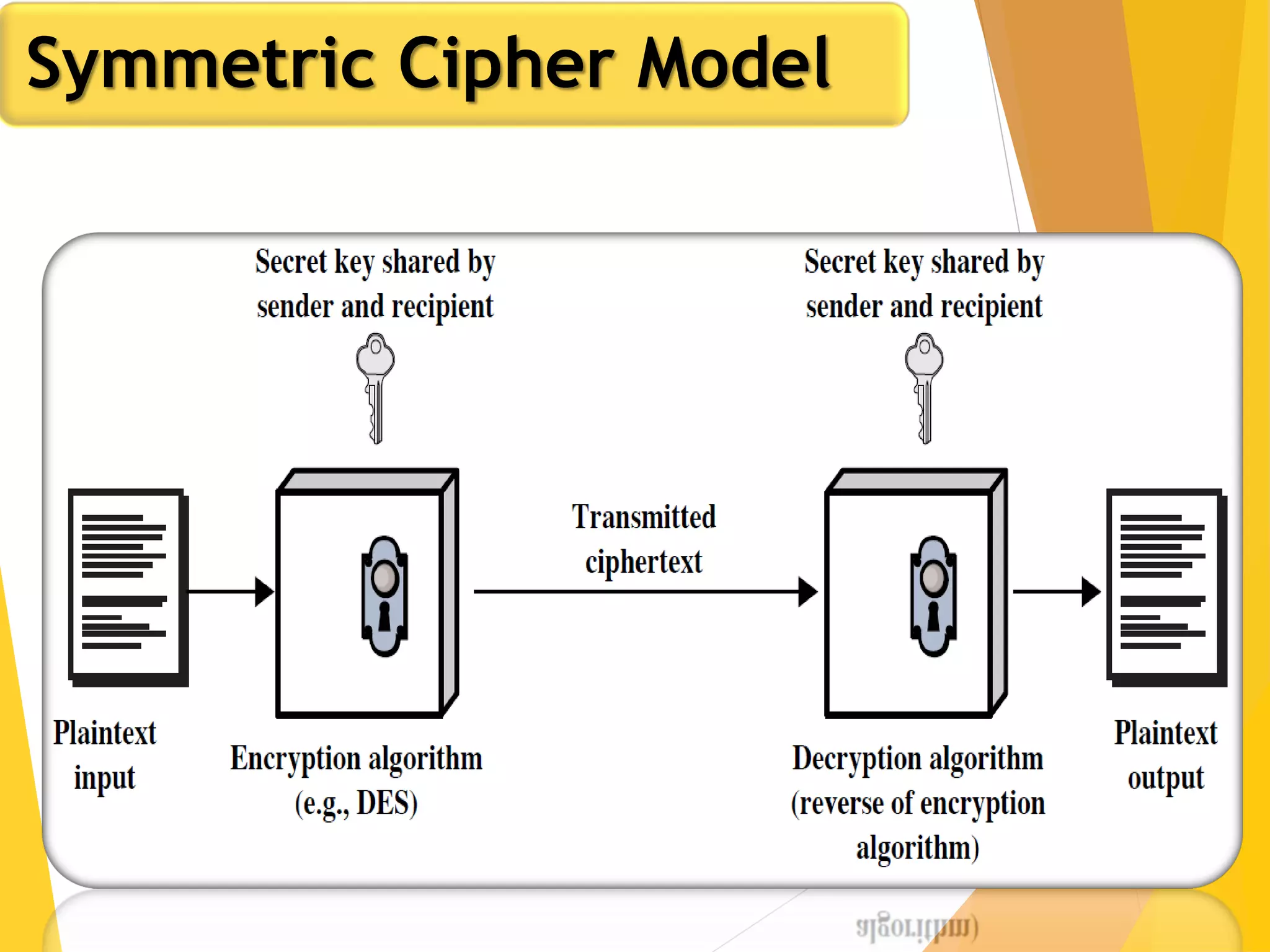
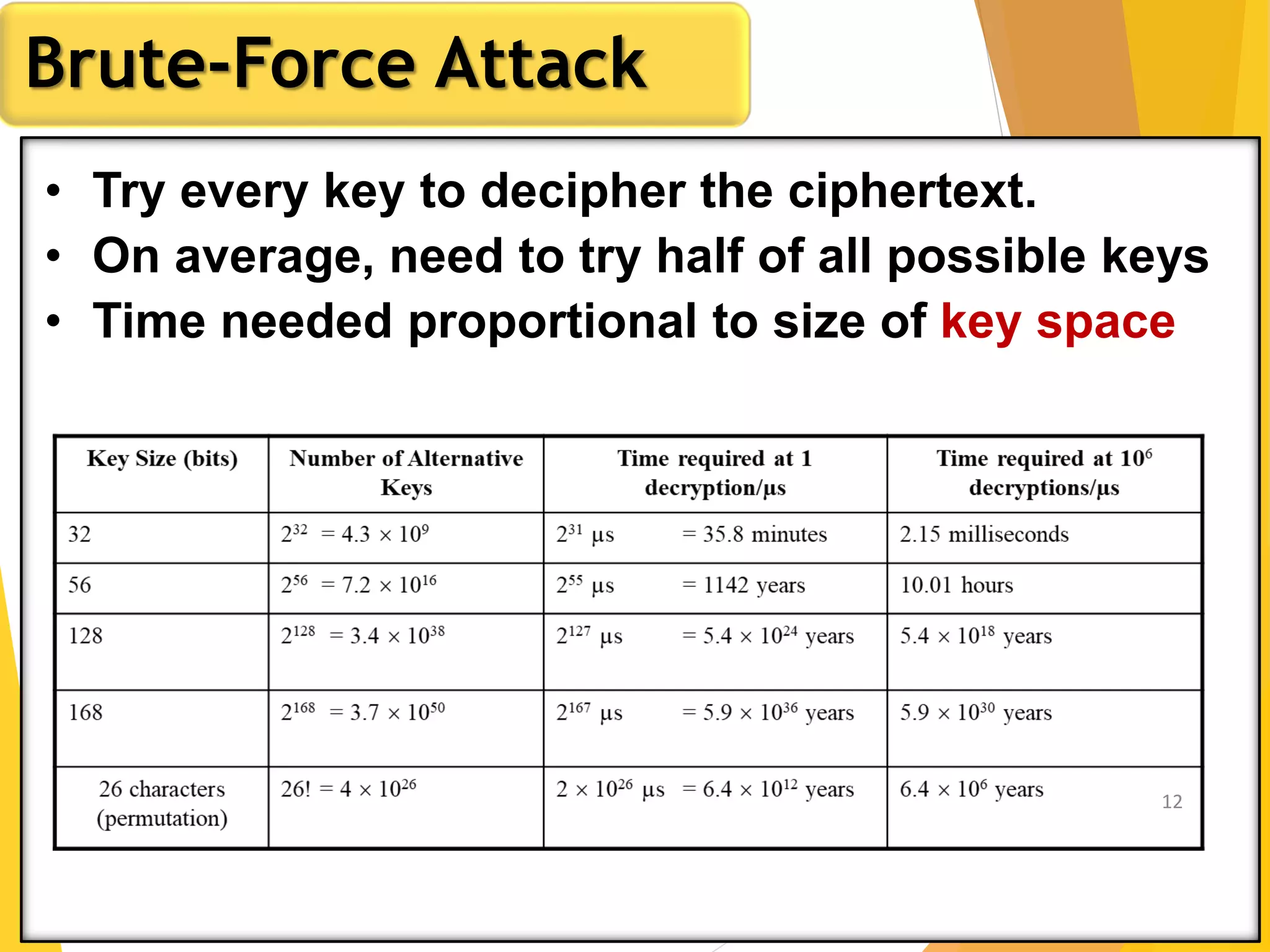
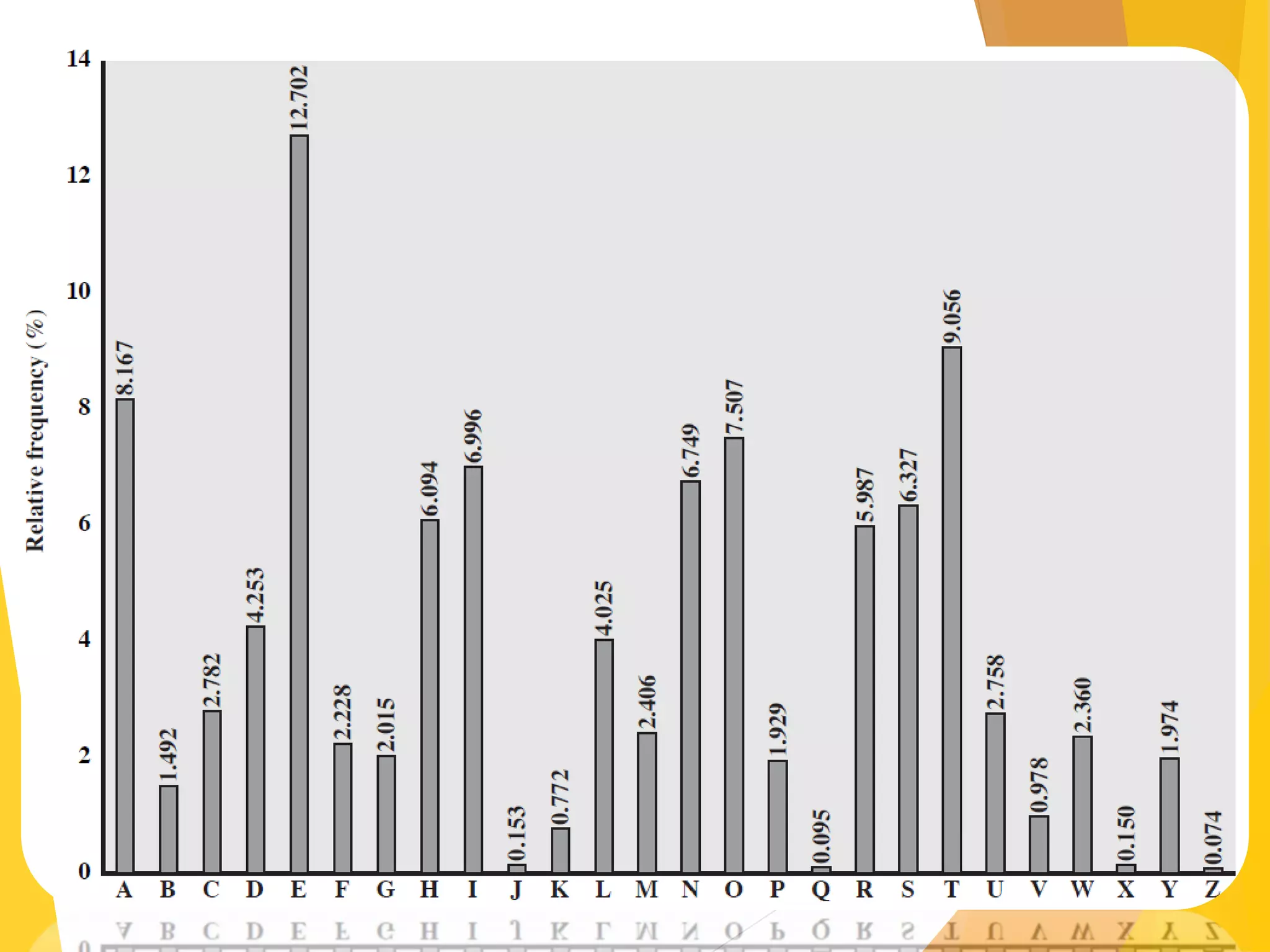
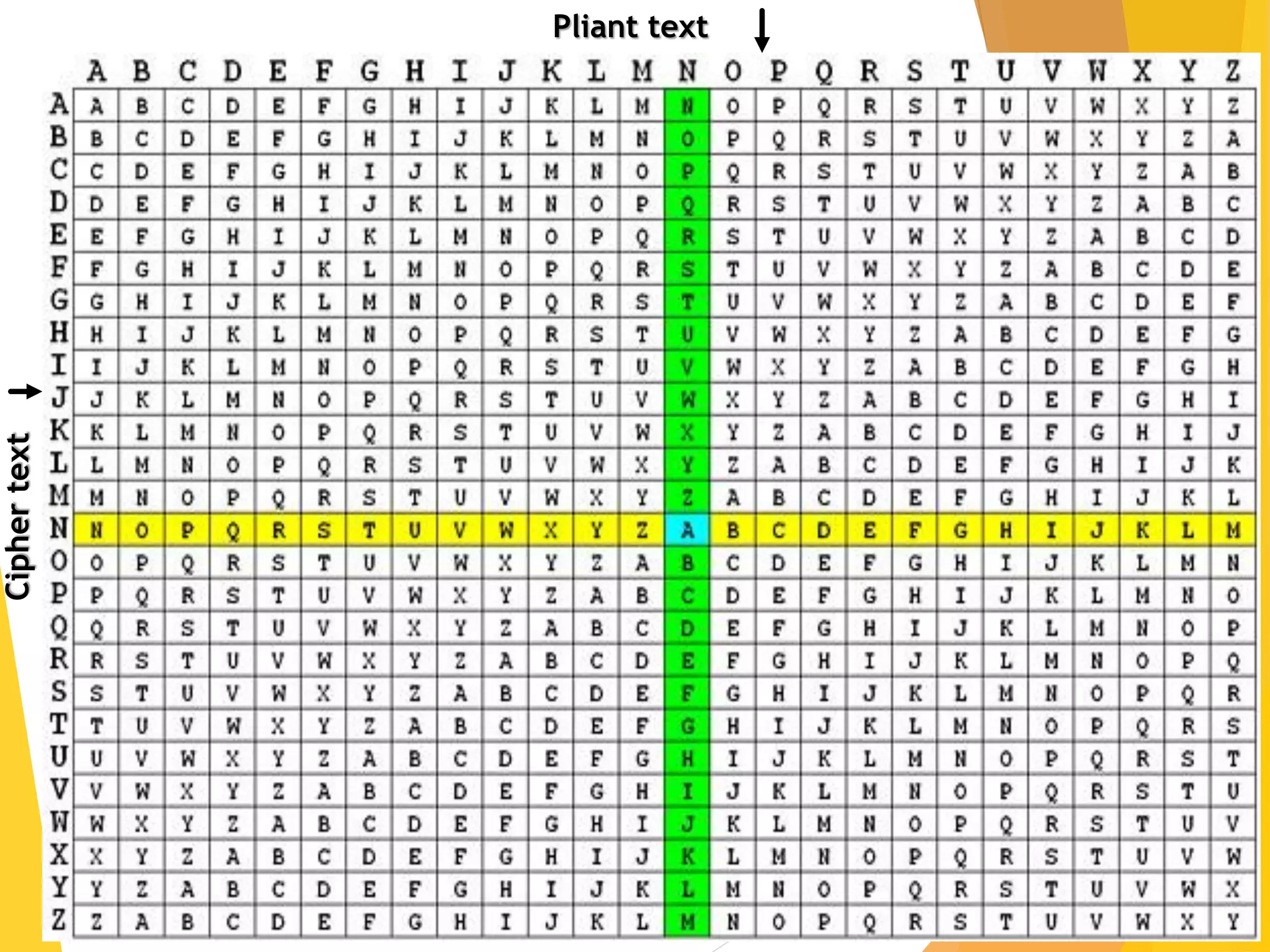
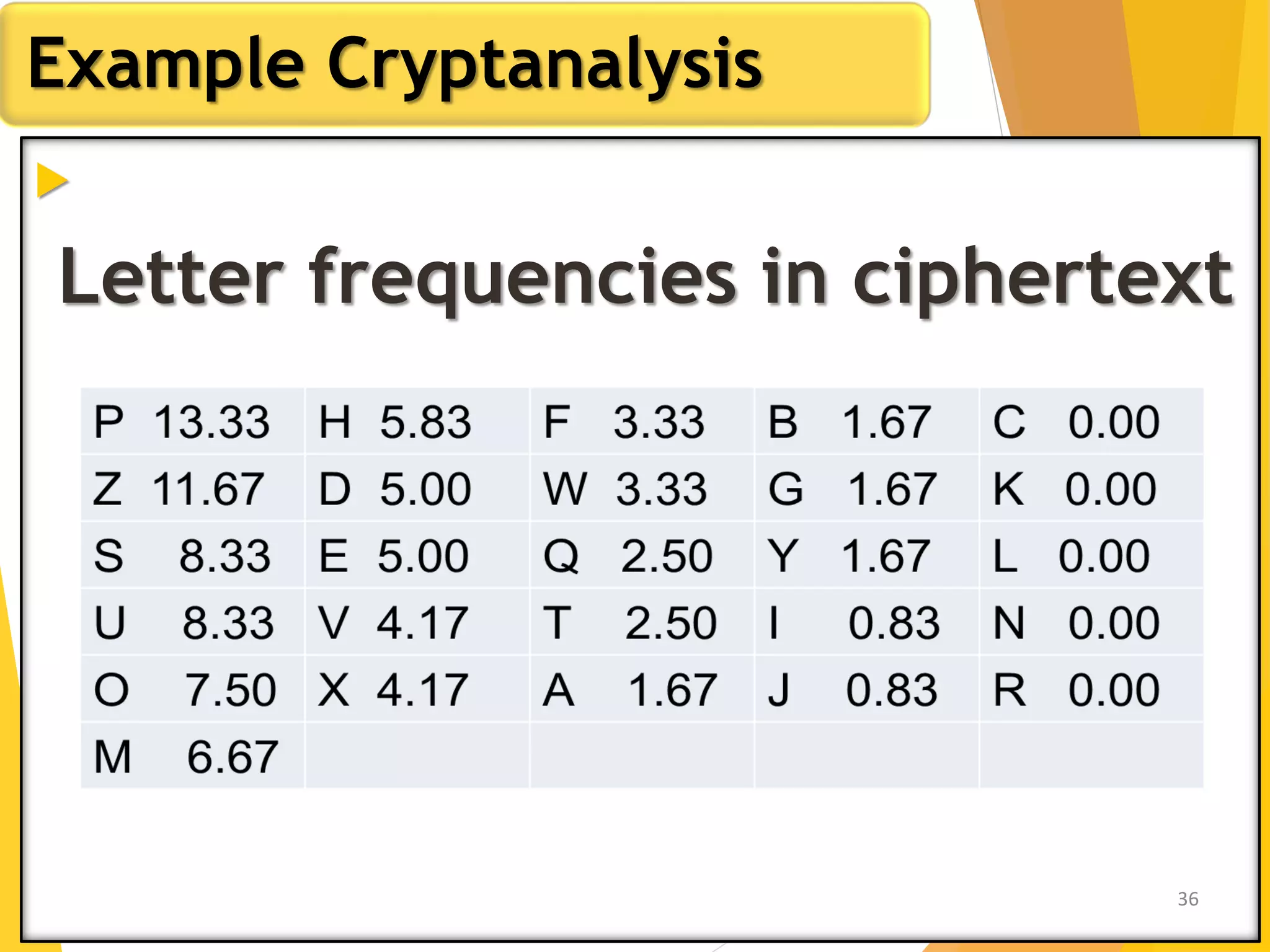
This document outlines the principles of network security, focusing on cryptography, classical encryption techniques, and various ciphers such as the Caesar cipher, Playfair cipher, and Vigenère cipher. It discusses symmetric and asymmetric encryption models, cryptanalysis methods, and the significance of key management in securing communications. Additionally, it covers the use of transposition and substitution ciphers, as well as steganography for hiding messages within other messages.
More Related Content
Network security CS2
- 1. Network Security CS-2 By: Prof.Ganesh Ingle
- 2. Session 2 objective Introduction Cryptography,Classical Encryption Breaking the Cryptosystem Modular Arithmetic, Groups and Rings Modular Arithmetic, Groups and Rings SUMMARY
- 3. Recorded Session Overview RL1.3.1= Reference Model for Network Security RL1.3.2 = Techniques to Implement Network Security - An Introduction RL2.1.1 = Overview - Layered Architecture in the service model and Networking Layers RL2.1.2 = Security at the application layers - objectives, issues and need. RL2.3.1 = Introduction to PGP RL2.3.2 = Integrity services through PGP RL2.3.3 = Confidentiality services through PGP RL2.3.4 = Brief discussion on the Cryptographic Algorithms used in PGP RL2.2.1 = E-Mail System Architecture
- 4. Cryptography, Classical Encryption Basicterminology 1. Plaintext: original message to be encrypted 2. Ciphertext: the encrypted message 3. Enciphering or encryption: the process of converting plaintext into ciphertext 4. Encryption algorithm: performs encryption 5. Two inputs: a plaintext and a secret key
- 5.
- 6. Deciphering or decryption:recovering plaintext from ciphertext Decryption algorithm: performs decryption Two inputs: ciphertext and secret key Secret key: same key used for encryption and decryption. Also referred to as a symmetric key Symmetric Cipher Model
- 7. Cipher or cryptographicsystem : A scheme for encryption and decryption Cryptography: Science of studying ciphers Cryptanalysis: Science of studying attacks against cryptographic systems Cryptology: cryptography + cryptanalysis Symmetric Cipher Model
- 8. Symmetric cipher:same key used for encryption and decryption Block cipher: encrypts a block of plaintext at a time (typically 64 or 128 bits) Stream cipher: encrypts data one bit or one byte at a time Asymmetric cipher: different keys used for encryption and decryption Ciphers
- 9. or conventional/ secret-key / single-key sender and recipient share a common key all classical encryption algorithms are symmetric The only type of ciphers prior to the invention of asymmetric-key ciphers in 1970’s by far most widely used Symmetric Encryption
- 10. Mathematically: Y =EK(X) or Y = E(K, X) X = DK(Y) or X = D(K, Y) X = plaintext Y = ciphertext K = secret key E = encryption algorithm D = decryption algorithm Both E and D are known to public Symmetric Encryption
- 11. Objective: torecover the plaintext of a ciphertext or, more typically, to recover the secret key. Kerkhoff’s principle: the adversary knows all details about a cryptosystem except the secret key. Two general approaches: brute-force attack non-brute-force attack (cryptanalytic attack) Cryptanalysis
- 12. Brute-Force Attack • Tryevery key to decipher the ciphertext. • On average, need to try half of all possible keys • Time needed proportional to size of key space 12
- 13. Plaintext isviewed as a sequence of elements (e.g., bits or characters) Substitution cipher: replacing each element of the plaintext with another element. Transposition (or permutation) cipher: rearranging the order of the elements of the plaintext. Product cipher: using multiple stages of substitutions and transpositions Classical Ciphers
- 14. Caesar Cipher ClassicalCiphers • Earliest known substitution cipher • Invented by Julius Caesar • Each letter is replaced by the letter three positions further down the alphabet. • Plain: a b c d e f g h i j k l m n o p q r s t u v w x y z Cipher: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C • Example: LOVE ??? 14
- 15. Caesar Cipher ClassicalCiphers • Mathematically, map letters to numbers: a, b, c, ..., x, y, z 0, 1, 2, ..., 23, 24, 25 • Then the general Caesar cipher is: c = EK(p) = (p + k) mod 26 p = DK(c) = (c – k) mod 26 • Can be generalized with any alphabet. • Vulnerable to brute-force attacks 15
- 16. Caesar Cipher ClassicalCiphers • Mathematically, map letters to numbers: a, b, c, ..., x, y, z 0, 1, 2, ..., 23, 24, 25 • Then the general Caesar cipher is: c = EK(p) = (p + k) mod 26 p = DK(c) = (c – k) mod 26 • Can be generalized with any alphabet. • Vulnerable to brute-force attacks 16
- 17. Monoalphabetic SubstitutionCipher Classical Ciphers • Shuffle the letters and map each plaintext letter to a different random ciphertext letter: • Plain letters: abcdefghijklmnopqrstuvwxyz • Cipher letters: DKVQFIBJWPESCXHTMYAUOLRGZN • Plaintext: ifwewishtoreplaceletters • Ciphertext: IRFRWAJUHYFTSDVFSFUUFYA • What does a key look like? • Now we have a total of 26! = 4 x 1026 keys. • With so many keys, it is secure against brute-force attacks. 17
- 18. Language Statisticsand Cryptanalysis Classical Ciphers – Human languages are not random. – Letters are not equally frequently used. – In English, E is by far the most common letter, followed by T, R, N, I, O, A, S. – Other letters like Z, J, K, Q, X are fairly rare. – There are tables of single, double & triple letter frequencies for various languages 18
- 20. Playfair Cipher Not even the large number of keys in a monoalphabetic cipher provides security. One approach to improving security is to encrypt multiple letters at a time. The Playfair Cipher is the best known such cipher. Invented by Charles Wheatstone in 1854, but named after his friend Baron Playfair. Classical Ciphers 20
- 21. Playfair Cipher Choose keyward (PLAYFAIRENCRPTION) 5x5 matrix enter element rowise left to right Fill matrix with rest of the characters Combine I and J in same cell Broke the PT into the group of alphabet(NAME) If both alphabets are same add x after first alphabet IF both alphabet appears in same row select next right alphabet IF both alphabet appears in same colum select next below alphabet Not in same row or column right below, left above Classical Ciphers 21
- 22. Playfair Cipher Choose keyward (PLAYFAIRENCRPTION) PT=NAME DIVIDE IN GROUP OF TWO NA=N and A are not in same row and column N=Y, A=E So NA =EY M=W, E=B So ME=WB PT=NAME CT=EYWB
- 23. Playfair Cipher Playfair Key Matrix Use a 5 x 5 matrix. Fill in letters of the key (w/o duplicates). Fill the rest of matrix with other letters. E.g., key = MONARCHY. Classical Ciphers 23
- 24. Encrypting andDecrypting Plaintext is encrypted two letters at a time. 1. If a pair is a repeated letter, insert filler like 'X’. 2. If both letters fall in the same row, replace each with the letter to its right (circularly). 3. If both letters fall in the same column, replace each with the the letter below it (circularly). 4. Otherwise, each letter is replaced by the letter in the same row but in the column of the other letter of the pair. 5. Security is much improved over the simple monoalphabetic cipher. 6. Was widely used for many decades 7. eg. by US & British military in WW1 and early WW2 Classical Ciphers 24
- 25. Polyalphabetic SubstitutionCiphers E.g. Vigenère Cipher A sequence of monoalphabetic ciphers (M1, M2, M3, ..., Mk) is used in turn to encrypt letters. A key determines which sequence of ciphers to use. Each plaintext letter has multiple corresponding ciphertext letters. This makes cryptanalysis harder since the letter frequency distribution will be flatter. Classical Ciphers 25
- 26. Vigenère Cipher Simplest polyalphabetic substitution cipher Consider the set of all Caesar ciphers: { Ca, Cb, Cc, ..., Cz } Key: e.g. security Encrypt each letter using Cs, Ce, Cc, Cu, Cr, Ci, Ct, Cy in turn. Repeat from start after Cy. Decryption simply works in reverse Classical Ciphers 26
- 27.
- 28. Vigenère Cipher(Poly alphabetic substitution) Plain text : MAKE IT HAPPEN Keyword :MATH M=12, A=0, T=19, H=7 Classical Ciphers 28 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 M A K E I T H A P P E N 12 0 19 7 12 0 19 7 12 0 19 7 Y A D L U T A H B P X U
- 29. Vigenère Cipher Simplest polyalphabetic substitution cipher Consider the set of all Caesar ciphers: { Ca, Cb, Cc, ..., Cz } Key: e.g. security Encrypt each letter using Cs, Ce, Cc, Cu, Cr, Ci, Ct, Cy in turn. Repeat from start after Cy. Decryption simply works in reverse Classical Ciphers 29
- 30. Vigenère Cipher Keyword: deceptive Key : deceptivedeceptivedeceptive Plaintext : wearediscoveredsaveyourself ciphertext: ZICVTWQNGRZGVTWAVZHCQYGLMGJ Classical Ciphers 30
- 31. Vigenère Cipher There are multiple (how many?) ciphertext letters corresponding to each plaintext letter. So, letter frequencies are obscured but not totally lost. To break Vigenere cipher: 1. Try to guess the key length. How? 2. If key length is N, the cipher consists of N Caesar ciphers. Plaintext letters at positions k, N+k, 2N+k, 3N+k, etc., are encoded by the same cipher. 3. Attack each individual cipher as before. Classical Ciphers 31
- 32. Transposition Ciphers Also called permutation ciphers. Shuffle the plaintext, without altering the actual letters used. Example: Row Transposition Ciphers Classical Ciphers 32
- 33. Row Transposition Ciphers Plaintext is written row by row in a rectangle. Ciphertext: write out the columns in an order specified by a key. Key: 3 4 2 1 5 6 7 Plaintext: Ciphertext: TTNAAPTMTSUOAODWCOIXKNLYPETZ a t t a c k p o s t p o n e d u n t i l t w o a m x y z 33 Classical Ciphers
- 34. 34 • Take a640x480 (=30,7200) pixel image. • Using only 1 LSB, can hide 115,200 characters • Using 4 LSBs, can hide 460,800 characters. Steganography Hide a message in another message. E.g., hide your plaintext in a graphic image Each pixel has 3 bytes specifying the RGB color The least significant bits of pixels can be changed w/o greatly affecting the image quality So can hide messages in these LSBs Advantage: hiding existence of messages Drawback: high overhead
- 35. Given ciphertext: UZQSOVUOHXMOPVGPOZPEVSGZWSZOPFPESXUDBMETSXAIZ VUEPHZHMDZSHZOWSFPAPPDTSVPQUZWYMXUZUHSX EPYEPOPDZSZUFPOMBZWPFUPZHMDJUDTMOHMQ Count relative letter frequencies (see next page) Guess {P, Z} = {e, t} Of double letters, ZW has highest frequency, so guess ZW = th and hence ZWP = the Proceeding with trial and error finally get: it was disclosed yesterday that several informal but direct contacts have been made with political representatives of the viet cong in moscow Example Cryptanalysis 35
- 36. Example Cryptanalysis 36 Letter frequenciesin ciphertext
- 37. Breaking theCryptosystem Given ciphertext: UZQSOVUOHXMOPVGPOZPEVSGZWSZOPFPESXUDBMETSXAIZ VUEPHZHMDZSHZOWSFPAPPDTSVPQUZWYMXUZUHSX EPYEPOPDZSZUFPOMBZWPFUPZHMDJUDTMOHMQ Count relative letter frequencies (see next page) Guess {P, Z} = {e, t} Of double letters, ZW has highest frequency, so guess ZW = th and hence ZWP = the Proceeding with trial and error finally get: it was disclosed yesterday that several informal but direct contacts have been made with political representatives of the viet cong in moscow Example Cryptanalysis 37
- 38. Have considered: classical cipher techniques and terminology monoalphabetic substitution ciphers cryptanalysis using letter frequencies Playfair cipher polyalphabetic ciphers transposition ciphers product ciphers and rotor machines stenography 38 Summary
- 39.